実行時間制限: 500 msec / メモリ制限: 64 MiB
配点: 100 点
あなたを乗せた超時空移民船は長旅の末,ついに居住可能と思われる惑星を発見した.JOI 星と名付けられたその惑星は,その名の通り「ジャングル (Jungle)」,「海 (Ocean)」,「氷 (Ice)」の 3 種類の地形が入り組んだ過酷な惑星である.簡単な調査により,居住予定地近辺の地図が作成された.
居住予定地は南北 M km,東西 N km の長方形の形をしており,1 km 四方の正方形の区画に分けられている.区画は全部で MN 個あり,北から p 行目,西から q 列目の区画を (p, q) で表す.北西の角の区画が (1, 1) であり,南東の角の区画が (M, N) である.各区画の地形は,「ジャングル」,「海」,「氷」のいずれかであり,「ジャングル」は J,「海」は O,「氷」は I の英字 1 文字で表される.
さて,詳細な移住計画を立てるにあたり,K 箇所の長方形領域内に「ジャングル」,「海」,「氷」がそれぞれ何区画含まれるかを調べることにした.
課題
居住予定地の情報と,調査対象となる領域の情報が与えられたとき,それぞれの領域について,「ジャングル」,「海」,「氷」が何区画含まれているかを求めるプログラムを作成せよ.
制限
| 1 \leqq M \leqq 1\,000 | 居住予定地の南北の長さ (km) |
| 1 \leqq N \leqq 1\,000 | 居住予定地の東西の長さ (km) |
| 1 \leqq K \leqq 100\,000 | 調査対象となる領域の個数 |
入力
標準入力から以下のデータを読み込め.
- 1 行目には整数 M, N が空白を区切りとして書かれており,居住予定地が南北に M km,東西に N km の広さであることを表す.
- 2 行目には整数 K が書かれており,調査対象となる領域の個数を表す.
- 続く M 行には居住予定地の情報が書かれている.i + 2 行目 (1 \leqq i \leqq M) には,居住予定地の北から i 行目に位置する N 区画の情報を表す
J,O,Iからなる N 文字の文字列が書かれている. - 続く K 行には調査対象となる領域が書かれている.j + M + 2 行目 (1 \leqq j \leqq K) には,j 番目の領域を表す正整数 a_j, b_j, c_j, d_j が空白を区切りとして書かれている.(a_j, b_j) は調査領域の北西の角の区画を,(c_j, d_j) は調査領域の南東の角の区画を表す.ただし,a_j, b_j, c_j, d_j は,1 \leqq a_j \leqq c_j \leqq M,1 \leqq b_j \leqq d_j \leqq N を満たす.
出力
標準出力に調査の結果を表す K 行を出力せよ.出力の j 行目には,j 番目の調査領域に含まれる「ジャングル」(J) の区画数,「海」(O) の区画数,「氷」(I) の区画数を表す 3 つの整数を,この順に空白を区切りとして書け.
採点基準
採点用データのうち,配点の 30 %分については,M \leqq 50 かつ K \leqq 100 を満たす.配点の 50 %分については,M \leqq 50 を満たす.
入力例 1
4 7 4 JIOJOIJ IOJOIJO JOIJOOI OOJJIJO 3 5 4 7 2 2 3 6 2 2 2 2 1 1 4 7
出力例 1
1 3 2 3 5 2 0 1 0 10 11 7

この入力例では, 2 番目の領域は上図のように「ジャングル」を 3 区画,「海」を 5 区画,「氷」を 2 区画含む.
出典
JOI 2010/2011 本選 問題1実行時間制限: 1 sec / メモリ制限: 64 MiB
配点: 100 点
あなたの町には JOI 古本店という老舗の古本屋があり,あなたは JOI 古本店をよく利用している.それぞれの本には基準価格が定まっており,JOI 古本店に行けばその価格で買い取ってもらえる.
JOI 古本店では,本を小説・漫画・雑誌など 10 種類のジャンルに分類して扱っている.ジャンルには 1 から 10 までの番号が付けられている.JOI 古本店には,同じジャンルの本をまとめて買い取ってもらうと高値で買い取ってくれるというサービスがある.具体的には,同じジャンルの本をまとめて T 冊買い取ってもらう場合,そのジャンルの本の一冊あたりの買取価格が基準価格より T − 1 円高くなる.例えば,同じジャンルで基準価格 100 円,120 円,150 円の本をまとめて JOI 古本店に売ったとすると,買取価格はそれぞれ 102 円,122 円,152 円となる.
さて,あなたは一身上の都合で急遽引越しをすることになった.あなたは N 冊の本を持っているが,新しい住居にすべての本を持っていくことは困難なため,N 冊の本のうち K 冊を JOI 古本店に売ることにした.
課題
N 冊の本それぞれの基準価格とジャンルの番号が与えられるとき,合計買取価格の最大値を求めるプログラムを作成せよ.
制限
| 2 \leqq N \leqq 2\,000 | あなたが持っている本の冊数 |
| 1 \leqq K < N | JOI 古本店に売る本の冊数 |
| 1 \leqq C_i \leqq 100\,000\,(=10^5) | i 番目の本の基準価格 |
| 1 \leqq G_i \leqq 10 | i 番目の本のジャンルの番号 |
入力
標準入力から以下の入力を読み込め.
- 1 行目には整数 N, K が空白を区切りとして書かれており,あなたの持っている本の冊数が N で,そのうち K 冊を JOI 古本店に売ることを表す.
- 続く N 行にはあなたの持っている本の情報が書かれている.i + 1 行目 (1\leqq i\leqq N) には,整数 C_i,G_i が空白を区切りとして書かれており,i 番目の本の基準価格が C_i で,ジャンルの番号が G_i であることを表す.
出力
標準出力に,合計買取価格の最大値を表す整数を 1 行で出力せよ.
採点基準
採点用データのうち,
配点の 20 %分については,N\leqq 20 を満たす.
配点の 20 %分については,すべての本のジャンルは 1 または 2 である.
配点の 10 %分については,これら 2 つの条件の両方を満たす.
配点の 30 %分については,これら 2 つの条件の少なくとも一方を満たす.
入力例 1
7 4 14 1 13 2 12 3 14 2 8 2 16 3 11 2
出力例 1
60
この入力例では,2 番目,4 番目,6 番目,7 番目の 4 冊の本を売ったとき,ジャンル 2 の本の買取価格が 1 冊あたり 2 円高くなるので,これらの本の買取価格は以下のようになる.
| 番号 | 基準価格 | ジャンル | 買取価格 |
|---|---|---|---|
| 2 | 13 | 2 | 15 |
| 4 | 14 | 2 | 16 |
| 6 | 16 | 3 | 16 |
| 7 | 11 | 2 | 13 |
よって合計買取価格は 15 + 16 + 16 + 13 = 60 円である.このとき合計買取価格は最大となる.
出典
JOI 2010/2011 本選 問題2実行時間制限: 500 msec / メモリ制限: 64 MiB
配点: 100 点
JOI 国には N 個の町があり,それらの間は M 本の双方向に通行可能な道路で結ばれている.K 個の町にはショッピングモールがあり,国民は道路を通ってそれらの町のいずれかに行き買い物をする.
家の場所によっては,買い物に行くために長い距離を移動する必要があり,それは非常に不便である.国王はこの実情を把握するため,ショッピングモールのある町までの最短距離が家の場所によってどれだけ長くなりうるのかを調べることにした.家は道路の途中に建てられることもあるので (入力例 1 の説明を参 照),この調査は非常に大変である.そこで国王は,優秀なプログラマーであるあなたに,調査を行うプログラムの作成を依頼した.
課題
道路の情報とショッピングモールのある町の情報が与えられるとき,ショッピングモールのある町からもっとも遠い道路上の点 (端点も含む) までの距離を求めるプログラムを作成せよ.町の中を移動するのにかかる距離は無視してよい.
制限
| 2 \leqq N \leqq 3\,000 | JOI 国の町の個数 |
| 1 \leqq M \leqq 100\,000\, (=10^5) | JOI 国の道路の本数 |
| 1 \leqq K\leqq N | ショッピングモールがある町の個数 |
| 1 \leqq l_i \leqq 1\,000 | i 番目の道路の長さ |
入力
標準入力から以下の入力を読み込め.
- 1 行目には整数 N, M, K が空白区切りで書かれている.N は JOI 国の町の個数を,M は JOI 国の道路の本数を,K はショッピングモールがある町の個数をそれぞれ表す.町には 1,2,\ldots,N の番号がつけ られている.
- 続く M 行は道路の情報を表す.i + 1 行目 (1\leqq i \leqq M) には整数 a_i,b_i,l_i (1\leqq a_i\leqq N,1\leqq b_i\leqq N,1\leqq l_i\leqq 1000) が空白区切りで書かれている.これは,i 本目の道路が町 a_i と町 b_i を結んでおり,長さが l_i であることを表す.道路の両端が同じ町であることはない.また,任意の 2 つの町 p, q に対し,p と q を結ぶ道路は 2 本以上存在しない.どの町からどの町へもいくつかの道路をたどって行くことができる.
- 続く K 行はショッピングモールの情報を表す.i + M + 1 行目 (1 \leqq i \leqq K) には 1 つの整数 s_i (1 \leqq s_i \leqq N) が書かれている.これは町 s_i にショッピングモールがあることを表す. s_1,\ldots, s_K の中に同じ値が 2 回以上現れることはない.
出力
標準出力に,ショッピングモールのある町までの最短距離の最大値の小数点以下を四捨五入した整数 1 つを出力せよ.
採点基準
採点用データのうち,配点の 40 %分については,K = 1 を満たす.
入力例 1
3 3 1 1 2 1 2 3 1 3 1 1 1
出力例 1
2
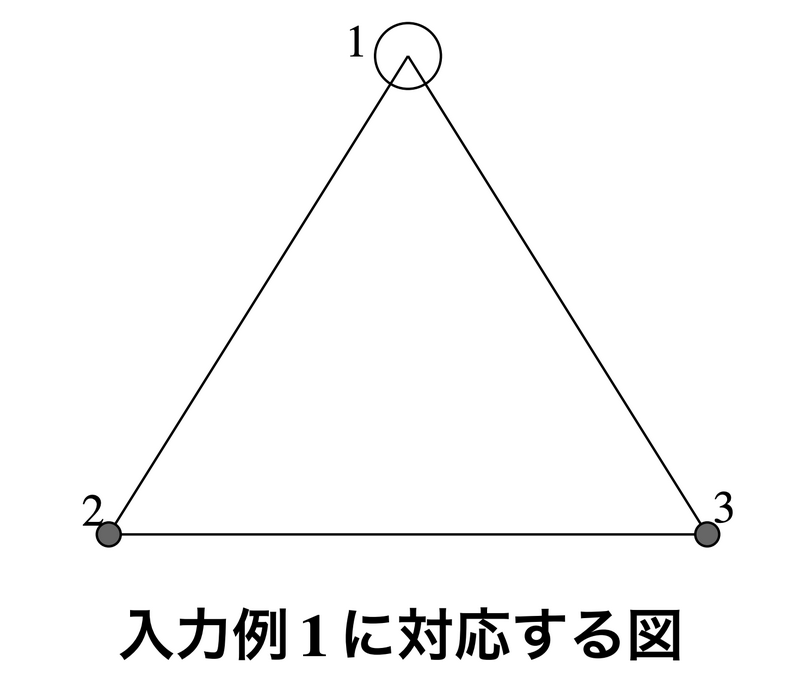
入力例 1 は次のような町を表す.道路の長さはすべて 1 である.ショッピングモールは町 1 にしかない.
ショッピングモールのある町までもっとも遠い点は,町 2 と町 3 を結ぶ道路上の,町 2 から距離 0.5 の位置にある点であり,ショッピングモールのある町までの距離は 1.5 である.よって,それを四捨五入した値である 2 を出力する.
入力例 2
4 5 2 1 2 4 1 3 1 2 3 2 2 4 2 3 4 1 2 4
出力例 2
3
出典
JOI 2010/2011 本選 問題3実行時間制限: 1 sec / メモリ制限: 64 MiB
配点: 100 点
昨年末,サンタクロースは JOI 村の子供たちにクリスマスプレゼントを渡すのを忘れてしまった.そこで,お詫びの気持ちとして子供たちにチョコレートケーキを届けることにした.届けるべき日は明日に迫っているので,そろそろ移動計画を考えなければならない.
JOI 村は,南北方向にまっすぐに伸びる W 本の道路と,東西方向にまっすぐに伸びる H 本の道路により,碁盤の目の形に区分けされている. 南北方向の W 本の道路には,西から順に 1,2,\ldots,W の番号が付けられており,東西方向の H 本の道路には,南から順に 1,2,\ldots,H の番号が付けられている. 西から x 番目の南北方向の道路と,南から y 番目の東西方向の道路が交わる交差点を (x, y) で表す. JOI 村には N 軒の家があ り,それらはいずれかの交差点に位置している. サンタクロースは道路に沿ってのみ移動することができる. 隣り合う交差点の間を移動するのにかかる時間を 1 とする.
JOI 村のすべての家には子供がいるので,サンタクロースは JOI 村のすべての家に 1 個ずつチョコレートケーキを届けてまわらなければならない. 大切なチョコレートケーキを持ってトナカイと空を飛びまわるのはやや危険であるので,サンタクロースとトナカイは JOI 村のいずれかの交差点に降り立ち,サンタクロースがそこから歩いてチョコレートケーキを届けることにした. サンタクロースは同時に 2 個以上のチョコレートケーキを運んで歩くことはしない.つまり,サンタクロースはチョコレートケーキを 1 軒の家に届けるたびに降り立った交差点に戻る.
サンタクロースは,JOI 村に降り立ってからすべての家にチョコレートケーキを届けるまでの所要時間が最小になるような移動計画を選ぶことにした.ここで,最後の家にチョコレートケーキを届けてから降り立った交差点に戻るまでの時間は所要時間に含めないことに注意せよ.また,移動にかかる時間以外は考えない.
課題
家の位置の情報が与えられたとき,サンタクロースが降り立つ交差点をうまく選んだ場合の,JOI 村に降り立ってからすべての家にチョコレートケーキを届けるまでの所要時間の最小値と,所要時間を最小にするために降り立つべき交差点の位置を求めるプログラムを作成せよ.
制限
| 1\leqq W\leqq 1\,000\,000\,000\,(=10^9) | 南北方向に伸びる道路の本数 |
| 1\leqq H\leqq 1\,000\,000\,000\,(=10^9) | 東西方向に伸びる道路の本数 |
| 1 \leqq N \leqq 100\,000\, (=10^5) | 家の数 |
| 1 \leqq X_i \leqq W | i 番目の家の位置の,南北方向に伸びる道路の番号 |
| 1 \leqq Y_i \leqq H | i 番目の家の位置の,東西方向に伸びる道路の番号 |
入力
標準入力から以下の入力を読み込め.
- 1 行目には各方向の道路の本数を表す整数 W, H が空白を区切りとして書かれている.
- 2 行目には家の数を表す整数 N が書かれている.
- 続く N 行には,家の位置の情報が書かれている.i + 2 行目 (1 \leqq i \leqq N) には整数 X_i,Y_i が空白を区切りとして書かれており,i 番目の家が交差点 (X_i, Y_i) に位置していることを表す.これら N 個の交差点はすべて異なる.
出力
標準出力に以下のデータを出力せよ.
- 1 行目には所要時間の最小値を表す 1 つの整数が書かれていなければならない.
- 2 行目には所要時間を最小にするために降り立つべき交差点が (x, y) であるとき,2 つの整数 x, y がこの順に空白を区切りとして書かれていなければならない.適切な交差点が複数ある場合は,そのうち最も西にある (つまり,x の値が小さい) 交差点を, それでも 1 つに定まらない場合は, さらにそのうちで最も南にある (つまり,y の値が小さい) 交差点を選べ.
注意
この問題では,扱う整数の範囲が 32 ビットに収まらない可能性があることに注意せよ.
採点基準
採点用データのうち,配点の 40 %分については,N \leqq 1\,000 を満たす.
採点用データのうち,配点の 10 %分については,W\leqq 50,H\leqq 50,N\leqq 1\,000 を満たす.
入力例 1
5 4 3 1 1 3 4 5 3
出力例 1
10 3 3
たとえば,次のような移動計画により所要時間を最小にできる.
- 交差点 (3, 3) に降り立つ.
- 交差点 (3, 4) に位置している家にチョコレートケーキを届ける.ここまでの経過時間は 1 である.
- 交差点 (3, 3) に戻る.ここまでの経過時間は 2 である.
- 交差点 (5, 3) に位置している家にチョコレートケーキを届ける.ここまでの経過時間は 4 である.
- 交差点 (3, 3) に戻る.ここまでの経過時間は 6 である.
- 交差点 (1, 1) に位置している家にチョコレートケーキを届ける.ここまでの経過時間は 10 である.
入力例 2
4 6 8 1 3 3 2 4 4 2 5 2 3 3 3 3 4 2 4
出力例 2
21 2 3
家がある交差点に降り立ってもよいことに注意せよ.
出典
JOI 2010/2011 本選 問題4実行時間制限: 1.5 sec / メモリ制限: 256 MiB
配点: 100 点
あなたは Just Odd Inventions 社を知っているだろうか? この会社の業務は「ただ奇妙な発明 (just odd inventions)」をすることである.ここでは略して JOI 社と呼ぶ.
JOI 社では多くの微生物を 1 つのシャーレに生きたまま閉じ込める研究をしている.調査対象の微生物は N 匹存在し,1,2,\ldots,N という番号がついている.各微生物はシャーレに閉じ込められると,foo (fatally odd object) と呼ばれる有害物質を一瞬のうちにシャーレ内に放出する.各微生物が放出する foo の量は知られている.シャーレに閉じ込められた全微生物が放出した foo はシャーレ内の各微生物が均等に摂取する.各微生物の foo 許容量は知られており,この量を超えて foo を摂取すると微生物は死んでしまう.
微生物 i の foo 放出量は a_i ミリグラム,foo 許容量は b_i ミリグラムである.すなわち,シャーレに微生物 i_1,i_2,\ldots,i_k を閉じ込めたとき,シャーレ内の各微生物はそれぞれ \displaystyle \frac{a_{i_1}+a_{i_2}+\cdots+a_{i_k}}k ミリグラムの foo を摂取し,シャーレ内の微生物 i は,この摂取量が b_i より大きいと死んでしまう.
JOI 社からの委託により,あなたは出来るだけ多くの微生物をシャーレに生きたまま閉じ込めなければならない.ただし,微生物の死骸はシャーレ内の環境に悪影響を及ぼすため,シャーレ内のどの微生物も foo の摂取で死んではならない.
なお,JOI 社が「ただ奇妙な発明」をすることでどうやって利益を得ているかは,今もって謎であり,JOI 社内でも社長以外の誰も知らない.
課題
調査対象の微生物数と,各微生物の foo 放出量と foo 許容量が与えられたとき,1 つのシャーレに閉じ込めることができる微生物数の最大値を求めるプログラムを作成せよ.
制限
| 1 \leqq N \leqq 300\,000\,(=3\times 10^5) | 調査対象の微生物の数 |
| 1 \leqq a_i \leqq 100\,000\, (=10^5) | 微生物 i の foo 放出量 (ミリグラム) |
| 1 \leqq b_i \leqq 100\,000\, (=10^5) | 微生物 i の foo 許容量 (ミリグラム) |
入力
標準入力から以下の入力を読み込め.
- 1 行目には整数 N が書かれており,調査対象の微生物が N 匹存在することを表す.
- 続く N 行には各微生物の情報が書かれている.i + 1 行目 (1\leqq i\leqq N) には,正整数 a_i,b_i が空白を区切りとして書かれており,微生物 i の foo 放出量が a_i ミリグラムで foo 許容量が b_i ミリグラムであることを表す.
出力
標準出力に,1 つのシャーレに閉じ込めることができる微生物数の最大値を 1 行で出力せよ.
注意
この問題では,扱う整数の範囲が 32 ビットに収まらない可能性があることに注意せよ.
採点基準
採点用データのうち,配点の 30 %分については,N\leqq 1\,000 を満たす.
入力例 1
6 12 8 5 9 2 4 10 12 6 7 13 9
出力例 1
3
この例では,微生物 2, 4, 5 をシャーレに入れれば,放出される foo の合計量は 5 + 10 + 6 = 21 ミリグラムとなり,それぞれの微生物が摂取する foo の量は \displaystyle \frac{21}3=7 ミリグラムとなる.微生物 2, 4, 5 の foo 許容量はそれぞれ 9, 12, 7 ミリグラムなので,シャーレ内のどの微生物も死なない.また,4 匹以上の微生物をどの微生物も死なないようにシャーレに入れることはできない.