白と黒の碁石をテーブルの上にならべて遊ぶ．まずテーブルの左端に碁石を置く． 次に左から 2 番目の場所に碁石を置く．これを n 回繰り返して n 個の碁石を横一列にならべる．ただし，新しく i 番目の碁石を置く際には，次のルールに従ってテーブル上の碁石を置き換える．

• i が奇数の場合: テーブルに置いてあった碁石は置き換えず，新しい碁石を左から i 番目に置く．
• i が偶数の場合: 新しく左から i 番目に置く碁石の色とテーブル上の右端の碁石の色が同じ場合は，テーブル上の碁石は置き換えず，新しい碁石を左から i 番目に置く．そうでない場合，すなわち，新しく左から i 番目に置く碁石の色とテーブル上の右端の碁石の色が異なる場合は，まずテーブル上の右端の連続した同色の碁石を全て取り除き，i 番目の碁石と同色の碁石に置き換える．そしてテーブルの右端に i 番目の碁石を置く．

例えば，最初の 7 個の碁石を置いた時点で，

\gdef\W{\Large \kern-0.05em\raisebox{-0.05em}{○}\kern-0.05em}\gdef\B{\Large \kern-0.05em\raisebox{-0.05em}{●}\kern-0.05em}\W\W\B\B\W\W\W

となっていたとする．（\W は白の碁石を，\B は黒の碁石を表す．）

• 8 番目の碁石が白（\W）の場合は，右端の碁石と同色なので，そのまま置く．したがって，テーブル上の碁石は \W\W\B\B\W\W\W\W となる．
• 8 番目の碁石が黒（\B）の場合は，右端の碁石（\W）と色が異なるので，まずテーブルの右端にある 3 個の連続した白い碁石（\W）を取り除き，黒い碁石（\B）に置き換える．そして右端に 8 番目の碁石を置く．したがって，テーブル上の碁石は \W\W\B\B\B\B\B\B となる．

入力として置く碁石の順番が与えられたとき，n 個の碁石をならべ終わった後，テーブル上に置いてある白い碁石の個数を求めるプログラムを作成せよ．

入力例 1

8
1
0
1
1
0
0
0
0

出力例 1

6

入力例 2

8
1
0
1
1
0
0
0
1

出力例 2

2

2 個の文字列が与えられたとき，両方の文字列に含まれる文字列のうち最も長いものを探し，その長さを答えるプログラムを作成せよ.

ここで，文字列 s が文字列 t に含まれるとは，t の中に s が連続して現れることをいう. 空文字列，すなわち長さ 0 の文字列は，どんな文字列にも含まれる. 例えば，文字列 ABRACADABRA には次の文字列が含まれる: ABRA，RAC，D，ACADABRA，ABRACADABRA，空文字列など. 一方，文字列 ABRACADABRA には次の文字列は含まれない: ABRC，RAA，BA，K など.

例

例 1: 文字列として ABRACADABRA と ECADADABRBCRDARA が与えられた場合,両方に含まれる文字列には CA や CADA や ADABR や空文字列などがある. そのうち最も長いのは ADABR であり，その長さは 5 である. 2 個の文字列の中に含まれる ADABR の位置を図 2-1 に示す.

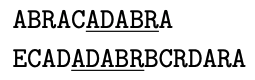
図 2-1 例 1 の文字列の中に現れる \texttt{ADABR} の位置

例 2: 文字列として UPWJCIRUCAXIIRGL と SBQNYBSBZDFNEV が与えられた場合，両方に含まれる文字列は空文字列のみであり，その長さは 0 である.

入力例 1

ABRACADABRA
ECADADABRBCRDARA

出力例 1

5

入力例 2

UPWJCIRUCAXIIRGL
SBQNYBSBZDFNEV

出力例 2

0

あなたは以下のルールでダーツゲームをすることになった．

あなたは，矢を的（まと）に向かって 4 本まで投げることができる．必ずしも 4 本全てを投げる必要はなく，1 本も投げなくてもかまわない．的は N 個の部分に区切られていて，各々の部分に点数 P_1,\ldots,P_N が書かれている．矢が刺さった場所の点数の合計 S があなたの得点の基礎となる．S があらかじめ決められたある点数 M 以下の場合は S がそのまま あなたの得点となる．しかし，S が M を超えた場合はあなたの得点は 0 点となる．

的に書かれている点数と M の値が与えられたとき，あなたが得ることのできる点数の最大値を求めるプログラムを作成せよ．

入力例 1

4 50
3
14
15
9

出力例 1

48

この例では，15 点の部分に 3 本，3 点の部分に 1 本の矢が刺さった場合にあなたの得点は最大になり，その得点は 48 点である．

入力例 2

3 21
16
11
2

出力例 2

20

この例では，16 点の場所に 1 本，2 点の場所に 2 本の矢が刺さった場合にあなたの得点は最大になり，その得点は 20 点である．

ある川で，一方の岸から石の上を次々と飛び移って反対側の岸まで行くという少々危険なゲームがはやっている．

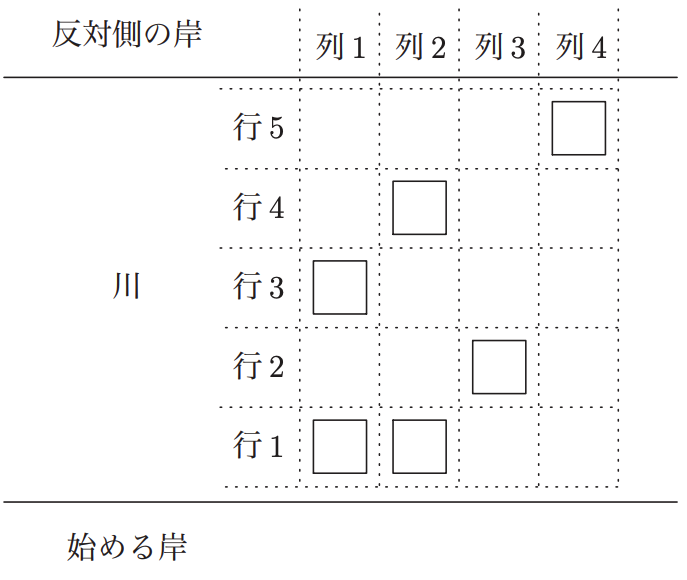
図 4-1 石の位置の例

今，図 4-1 のように，石はマス目の上に存在すると考える．行の数は n である． 図 4-1 では n = 5 である．

このゲームでは，一方の岸から始めて，通常のジャンプまたは m 回以下の一行飛 ばしのジャンプをして反対側の岸まで渡る．通常のジャンプとは，今いる行の一つ先 の行の岸または石のどれかに飛び移ることであり，一行飛ばしのジャンプとは，今 いる行の二つ先の行の岸または石のどれかに飛び移ることである．始める岸の一つ 先の行は 1 行目，二つ先の行は 2 行目であり，n − 1 行目の二つ先の行，及び n 行目の一つ先の行は反対側の岸であるとする．

さて，このゲームをできるだけ安全に成し遂げるために，ジャンプの危険度とい うものを考えることにした．それぞれの石には，滑りやすさが定まっている．石か ら石へ飛び移る際のジャンプの危険度は，通常のジャンプであっても，一行飛ばし のジャンプであっても，

• （今いる石の滑りやすさ + 飛び移る先の石の滑りやすさ）\times（横の移動距離） で定める．ただし，横の移動距離とは，列の番号の差である．また，岸から石へ，あ るいは石から岸へ飛び移るジャンプの危険度は 0 とする．

入力として n， m，それぞれの石の位置と滑りやすさが与えられたとき，反対側の岸まで到達する際のジャンプの危険度の合計の最小値を求めるプログラムを作成せよ．与えられる入力データは必ず反対側の岸まで到達することができるようになっており，同じマス目に石は 2 個以上存在しない．

例

図 4-2 において，石に書かれた数字はそれぞれの石の滑りやすさを表すとする．

矢印で示された順番で石を渡るとき，それぞれのジャンプの危険度は，順番に 0，(2 + 2) \times 1 = 4，(2 + 1) \times 1 = 3，(1 + 4) \times 2 = 10，0 であり，合計は 17 となる．このとき，ジャンプの危険度の合計は最小となる．

この例は入出力例に対応している．

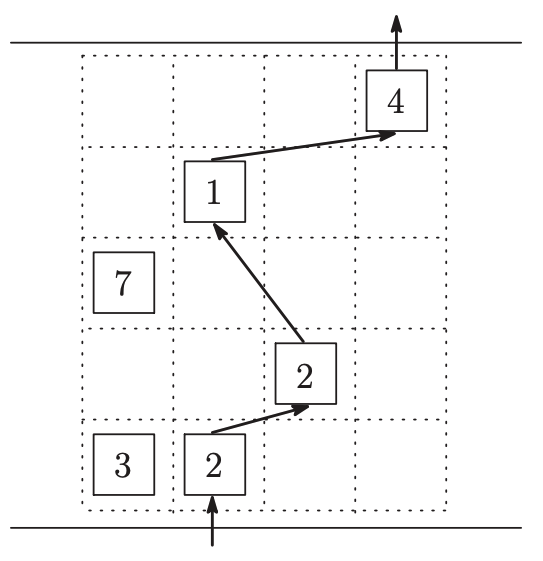
図 4-2 経路の例

入力例 1

5 1
2 1 3 2 2
1 3 2
1 1 7
1 2 1
1 4 4

出力例 1

17

上の例に対応する入出力は例 1 の通りである．

入力例 2

5 0
2 1 3 2 2
1 3 2
1 1 7
1 2 1
1 4 4

出力例 2

40

情報オリンピックの宣伝のために，長方形のベニヤ板にペンキを塗り看板を制作したい．ベニヤ板には色を塗りたくないところにあらかじめ何枚かの長方形のマスキングテープが貼られている．そこでマスキングテープで区切られた領域ごとに別々の色を使いペンキを塗ることにした．例えば，図 5-1 の場合は 5 色のペンキを使う．

図 5-1 看板の例

入力としてマスキングテープを貼る位置が与えられた時，使うペンキの色の数を求めるプログラムを作成せよ．ただし，ベニヤ板全体がマスキングテープで覆われることはなく，全てのマスキングテープの辺はベニヤ板のいずれかの辺に平行である．

入力例 1

15 6
10
1 4 5 6
2 1 4 5
1 0 5 1
6 1 7 5
7 5 9 6
7 0 9 2
9 1 10 5
11 0 14 1
12 1 13 5
11 5 14 6

出力例 1

5

この例は図 5-1 の場合である．