Problem Statement

You are given a string $S$, which is balanced parentheses with a star symbol * inserted.

Any balanced parentheses can be constructed using the following rules:

• An empty string is balanced.
• Concatenation of two balanced parentheses is balanced.
• If $T$ is balanced parentheses, concatenation of (, $T$, and ) in this order is balanced.

For example, ()() and (()()) are balanced parentheses. )( and )()(() are not balanced parentheses.

Your task is to count how many matching pairs of parentheses surround the star.

Let $S_i$ be the $i$-th character of a string $S$. The pair of $S_l$ and $S_r$ $(l < r)$ is called a matching pair of parentheses if $S_l$ is (, $S_r$ is ) and the surrounded string by them is balanced when ignoring a star symbol.

Input

The input consists of a single test case formatted as follows.

$S$

$S$ is balanced parentheses with exactly one * inserted somewhere. The length of $S$ is between $1$ and $100$, inclusive.

Output

Print the answer in one line.

Sample Input 1

((*)())

Output for Sample Input 1

2

Sample Input 2

(*)

Output for Sample Input 2

1

Sample Input 3

(()())*

Output for Sample Input 3

0

Sample Input 4

()*()

Output for Sample Input 4

0

Sample Input 5

((((((((((*))))))))))

Output for Sample Input 5

10

Sample Input 6

*

Output for Sample Input 6

0

Problem Statement

Chokudai loves eating so much. However, his doctor Akensho told him that he was overweight, so he finally decided to lose his weight.

Chokudai made a slimming plan of a $D$-day cycle. It is represented by $D$ integers $w_0, \ldots, w_{D-1}$. His weight is $S$ on the $0$-th day of the plan and he aims to reduce it to $T \ (S > T)$. If his weight on the $i$-th day of the plan is $x$, it will be $x + w_{i \% D}$ on the $(i+1)$-th day. Note that $i \% D$ is the remainder obtained by dividing $i$ by $D$. If his weight successfully gets less than or equal to $T$, he will stop slimming immediately.

If his slimming plan takes too many days or even does not end forever, he should reconsider it.

Determine whether it ends or not, and report how many days it takes if it ends.

Input

The input consists of a single test case formatted as follows.

$S \ T \ D$ $w_0 \cdots w_{D-1}$

The first line consists of three integers $S, T, D \ (1 \le S,T,D \le 100{,}000, \ S > T)$. The second line consists of $D$ integers $w_0, \ldots, w_{D-1}$ ($-100{,}000 \le w_i \le 100{,}000$ for each $i$).

Output

If Chokudai's slimming plan ends on the $d$-th day, print $d$ in one line. If it never ends, print $-1$.

Sample Input 1

65 60 3
-2 3 -4

Output for Sample Input 1

4

Chokudai's weight will change as follows: $65 \to 63 \to 66 \to 62 \to 60$.

Sample Input 2

65 60 3
-2 10 -3

Output for Sample Input 2

-1

Chokudai's weight will change as follows: $65 \to 63 \to 73 \to 70 \to 68 \to 78 \to 75 \to \cdots$.

Sample Input 3

100000 1 1
-1

Output for Sample Input 3

99999

Sample Input 4

60 59 1
-123

Output for Sample Input 4

1

Problem Statement

Intersections of Crossing Path City are aligned to a grid. There are $N$ east-west streets which are numbered from 1 to $N$, from north to south. There are also $N$ north-south streets which are numbered from 1 to $N$, from west to east. Every pair of east-west and north-south streets has an intersection; therefore there are $N^2$ intersections which are numbered from 1 to $N^2$.

Surprisingly, all of the residents in the city are Ninja. To prevent outsiders from knowing their locations, the numbering of intersections is shuffled.

You know the connections between the intersections and try to deduce their positions from the information. If there are more than one possible set of positions, you can output any of them.

Input

The input consists of a single test case formatted as follows.

$N$ $a_1 \ b_1$ $\cdots$ $a_{2N^2-2N} \ b_{2N^2-2N}$

The first line consists of an integer $N \ (2 \le N \le 100)$. The following $2N^2-2N$ lines represent connections between intersections. The $(i+1)$-th line consists of two integers $a_i$ and $b_i$ ($1 \le a_i, b_i \le N^2$, $a_i \ne b_i$), which represent that the $a_i$-th and $b_i$-th intersections are adjacent. More precisely, let's denote by $(r, c)$ the intersection of the $r$-th east-west street and the $c$-th north-south street. If the intersection number of $(r, c)$ is $a_i$ for some $r$ and $c$, then the intersection number of either $(r - 1, c)$, $(r + 1, c)$, $(r, c - 1)$ or $(r, c + 1)$ must be $b_i$. All inputs of adjacencies are different, i.e., $(a_i,b_i)\ne(a_j,b_j)$ and $(a_i,b_i)\ne(b_j,a_j)$ for all $1 \le i < j \le 2N^2-2N$. This means that you are given information of all adjacencies on the grid.

The input is guaranteed to describe a valid map.

Output

Print a possible set of positions of the intersections. More precisely, the output consists of $N$ lines each of which has space-separated $N$ integers. The $c$-th integer of the $r$-th line should be the intersection number of $(r, c)$.

If there are more than one possible set of positions, you can output any of them.

Sample Input 1

3
1 2
4 7
8 6
2 3
8 9
5 3
4 6
5 6
7 8
1 4
2 6
5 9

Output for Sample Input 1

7 4 1
8 6 2
9 5 3

The following output will also be accepted.

1 2 3
4 6 5
7 8 9

Sample Input 2

4
12 1
3 8
10 7
13 14
8 2
9 12
6 14
11 3
3 13
1 10
11 15
4 15
4 9
14 10
5 7
2 5
6 1
14 5
16 11
15 6
15 13
9 6
16 4
13 2

Output for Sample Input 2

8 2 5 7
3 13 14 10
11 15 6 1
16 4 9 12

Problem Statement

You are supposed to play the rock-paper-scissors game. There are $N$ players including you.

This game consists of multiple rounds. While the rounds go, the number of remaining players decreases. In each round, each remaining player will select an arbitrary shape independently. People who show rocks win if all of the other people show scissors. In this same manner, papers win rocks, scissors win papers. There is no draw situation due to the special rule of this game: if a round is tied based on the normal rock-paper-scissors game rule, the player who has the highest programming contest rating (this is nothing to do with the round!) will be the only winner of the round. Thus, some players win and the other players lose on each round. The losers drop out of the game and the winners proceed to a new round. They repeat it until only one player becomes the winner.

Each player is numbered from $1$ to $N$. Your number is $1$. You know which shape the other $N-1$ players tend to show, that is to say, you know the probabilities each player shows rock, paper and scissors. The $i$-th player shows rock with $r_i$% probability, paper with $p_i$% probability, and scissors with $s_i$% probability. The rating of programming contest of the player numbered $i$ is $a_i$. There are no two players whose ratings are the same. Your task is to calculate your probability to win the game when you take an optimal strategy based on each player's tendency and rating.

Input

The input consists of a single test case formatted as follows.

$N$ $a_1$ $a_2 \ r_2 \ p_2 \ s_2$ $\vdots$ $a_N \ r_N \ p_N \ s_N$

The first line consists of a single integer $N \ (2 \le N \le 14)$. The second line consists of a single integer $a_1 \ (1 \le a_1 \le N)$. The $(i+1)$-th line consists of four integers $a_i$, $r_i$, $p_i$ and $s_i$ ($1 \le a_i \le N$, $0 \le r_i, p_i, s_i \le 100$, $r_i + p_i + s_i = 100$) for $i = 2, \ldots, N$. It is guaranteed that $a_1, \ldots, a_N$ are pairwise distinct.

Output

Print the probability to win the game in one line. Your answer will be accepted if its absolute or relative error does not exceed $10^{-6}$.

Sample Input 1

2
2
1 40 40 20

Output for Sample Input 1

0.8

Since you have the higher rating than the other player, you will win the game if you win or draw in the first round.

Sample Input 2

2
1
2 50 50 0

Output for Sample Input 2

0.5

You must win in the first round.

Sample Input 3

3
2
1 50 0 50
3 0 0 100

Output for Sample Input 3

1

In the first round, your best strategy is to show a rock. You will win the game with 50% in this round. With the other 50%, you and the second player proceed to the second round and you must show a rock to win the game.

Sample Input 4

3
2
3 40 40 20
1 30 10 60

Output for Sample Input 4

0.27

Sample Input 5

4
4
1 34 33 33
2 33 34 33
3 33 33 34

Output for Sample Input 5

0.6591870816

Problem Statement

You have a grid with $H$ rows and $W$ columns. $H+W$ is even. We denote the cell at the $i$-th row from the top and the $j$-th column from the left by $(i, j)$. In any cell $(i, j)$, an integer between $1$ and $9$ is written if $i+j$ is even, and either + or * is written if $i+j$ is odd.

You can get a mathematical expression by moving right or down $H+W-2$ times from $(1,1)$ to $(H,W)$ and concatenating all the characters written in the cells you passed in order. Your task is to maximize the calculated value of the resulting mathematical expression by choosing an arbitrary path from $(1, 1)$ to $(H, W)$. If the maximum value is $10^{15}$ or less, print the value. Otherwise, print $-1$.

Input

The input consists of a single test case in the format below.

$H$ $W$ $a_{1,1}$ $\cdots$ $a_{1,W}$ $\ldots$ $a_{H,1}$ $\cdots$ $a_{H,W}$

The first line consists of two integers $H$ and $W$ ($1 \le H,W \le 50$). It is guaranteed that $H+W$ is even. The following $H$ lines represent the characters on the grid. $a_{i,j}$ represents the character written in the cell $(i,j)$. In any cell $(i, j)$, an integer between $1$ and $9$ is written if $i+j$ is even, and either + or * is written if $i+j$ is odd.

Output

Print the answer in one line.

Sample Input 1

3 3
1+2
+9*
1*5

Output for Sample Input 1

46

The maximum value is obtained by passing through the following cells: $(1,1)$, $(2,1)$, $(2,2)$, $(2,3)$, $(3,3)$.

Sample Input 2

1 31
9*9*9*9*9*9*9*9*9*9*9*9*9*9*9*9

Output for Sample Input 2

-1

You can obtain $9^{16}$, but it's too large.

Sample Input 3

5 5
2+2+1
+1+1+
1+2+2
+1+1+
1+1+2

Output for Sample Input 3

10

Sample Input 4

9 7
8+9*4*8
*5*2+3+
1*3*2*2
*5*1+9+
1+2*2*2
*3*6*2*
7*7+6*5
*5+7*2+
3+3*6+8

Output for Sample Input 4

86408

Problem Statement

Mr. Endo wanted to write the code that performs breadth-first search (BFS), which is a search algorithm to explore all vertices on an undirected graph. An example of pseudo code of BFS is as follows:

1: $current \leftarrow \{start\_vertex\}$ 2: $visited \leftarrow current$ 3: while $visited \ne$ the set of all the vertices 4: $found \leftarrow \{\}$ 5: for $v$ in $current$ 6: for each $u$ adjacent to $v$ 7: $found \leftarrow found \cup \{u\}$ 8: $current \leftarrow found \setminus visited$ 9: $visited \leftarrow visited \cup found$

However, Mr. Endo apparently forgot to manage visited vertices in his code. More precisely, he wrote the following code:

1: $current \leftarrow \{start\_vertex\}$ 2: while $current \ne$ the set of all the vertices 3: $found \leftarrow \{\}$ 4: for $v$ in $current$ 5: for each $u$ adjacent to $v$ 6: $found \leftarrow found \cup \{u\}$ 7: $current \leftarrow found$

You may notice that for some graphs, Mr. Endo's program will not stop because it keeps running infinitely. Notice that it does not necessarily mean the program cannot explore all the vertices within finite steps. See example 2 below for more details.Your task here is to make a program that determines whether Mr. Endo's program will stop within finite steps for a given graph in order to point out the bug to him. Also, calculate the minimum number of loop iterations required for the program to stop if it is finite.

Input

The input consists of a single test case formatted as follows.

$N$ $M$ $U_{1}$ $V_{1}$ $\vdots$ $U_{M}$ $V_{M}$

The first line consists of two integers $N$ ($2 \le N \le 100{,}000$) and $M$ ($1 \le M \le 100{,}000$), where $N$ is the number of vertices and $M$ is the number of edges in a given undirected graph, respectively. The $i$-th line of the following $M$ lines consists of two integers $U_{i}$ and $V_{i}$ ($1 \le U_{i}, V_{i} \le N$), which means the vertices $U_{i}$ and $V_{i}$ are adjacent in the given graph. The vertex 1 is the start vertex, i.e. $start\_vertex$ in the pseudo codes. You can assume that the given graph also meets the following conditions.

• The graph has no self-loop, i.e., $U_{i} \ne V_{i}$ for all $1 \le i \le M$.
• The graph has no multi-edge, i.e., $\{U_{i}, V_{i}\} \ne \{U_{j}, V_{j}\} $ for all $1 \le i < j \le M$.
• The graph is connected, i.e., there is at least one path from $U$ to $V$ (and vice versa) for all vertices $1 \le U, V \le N$.

Output

If Mr. Endo's wrong BFS code cannot stop within finite steps for the given input graph, print -1 in a line. Otherwise, print the minimum number of loop iterations required to stop.

Sample Input 1

3 3
1 2
1 3
2 3

Output for Sample Input 1

2

Sample Input 2

4 3
1 2
2 3
3 4

Output for Sample Input 2

-1

Transition of $current$ is $\{1\} \rightarrow \{2\} \rightarrow \{1, 3\} \rightarrow \{2, 4\} \rightarrow \{1, 3\} \rightarrow \{2, 4\} \rightarrow \cdots$. Although Mr. Endo's program will achieve to visit all the vertices (in 3 steps), $current$ will never become the same set as all the vertices.

Sample Input 3

4 4
1 2
2 3
3 4
4 1

Output for Sample Input 3

-1

Sample Input 4

8 9
2 1
3 5
1 6
2 5
3 1
8 4
2 7
7 1
7 4

Output for Sample Input 4

3

Problem Statement

You received a card at a banquet. On the card, a matrix of $N$ rows and $M$ columns and two integers $K$ and $S$ are written. All the elements in the matrix are integers, and an integer at the $i$-th row from the top and the $j$-th column from the left is denoted by $A_{i,j}$.

You can select up to $K$ elements from the matrix and invert the sign of the elements. If you can make a matrix such that there is no vertical or horizontal contiguous subsequence whose sum is greater than $S$, you can exchange your card for a prize.

Your task is to determine if you can exchange a given card for a prize.

Input

The input consists of a single test case of the following form.

$N$ $M$ $K$ $S$ $A_{1,1}$ $A_{1,2}$ $\cdots$ $A_{1,M}$ $\vdots$ $A_{N,1}$ $A_{N,2}$ $\cdots$ $A_{N,M}$

The first line consists of four integers $N$, $M$, $K$, and $S$ ($1 \le N, M \le 10$, $1 \le K \le 5$, $1 \le S \le 10^6$). The following $N$ lines represent the matrix in your card. The $(i+1)$-th line consists of $M$ integers $A_{i,1}$, $A_{i,2}$, $\ldots$, $A_{i,M}$ ($-10^5 \le A_{i,j} \le 10^5$).

Output

If you can exchange your card for a prize, print Yes. Otherwise, print No.

Sample Input 1

3 3 2 10
5 3 7
2 6 1
3 4 1

Output for Sample Input 1

Yes

The sum of a horizontal contiguous subsequence from $A_{1,1}$ to $A_{1,3}$ is $15$. The sum of a vertical contiguous subsequence from $A_{1,2}$ to $A_{3,2}$ is $13$. If you flip the sign of $A_{1,2}$, there is no vertical or horizontal contiguous subsequence whose sum is greater than $S$.

Sample Input 2

2 3 1 5
4 8 -2
-2 -5 -3

Output for Sample Input 2

Yes

Sample Input 3

2 3 1 5
9 8 -2
-2 -5 -3

Output for Sample Input 3

No

Sample Input 4

2 2 3 100
0 0
0 0

Output for Sample Input 4

Yes

Problem Statement

You are an employee of Automatic Cleaning Machine (ACM) and a member of the development team of Intelligent Circular Perfect Cleaner (ICPC). ICPC is a robot that cleans up the dust of the place which it passed through.

Your task is an inspection of ICPC. This inspection is performed by checking whether the center of ICPC reaches all the $N$ given points.

However, since the laboratory is small, it may be impossible to place all the points in the laboratory so that the entire body of ICPC is contained in the laboratory during the inspection. The laboratory is a rectangle of $H \times W$ and ICPC is a circle of radius $R$. You decided to write a program to check whether you can place all the points in the laboratory by rotating and/or translating them while maintaining the distance between arbitrary two points.

Input

The input consists of a single test case of the following format.

$N$ $H$ $W$ $R$ $x_1$ $y_1$ $\vdots$ $x_N$ $y_N$

The first line consists of four integers $N$, $H$, $W$, and $R$ ($1 \le N \le 100$, $1 \le H, W \le 10^9$, $1 \le R \le 10^6$). The following $N$ lines represent the coordinates of the points which the center of ICPC must reach. The $(i+1)$-th line consists of two integers $x_i$ and $y_i$ ($0 \le x_i, y_i \le 10^9$). $x_i$ and $y_i$ represent the $x$ and $y$ coordinates of the $i$-th point, respectively. It is guaranteed that the answer will not change even if $R$ changes by $1$.

Output

If all the points can be placed in the laboratory, print Yes. Otherwise, print No.

Sample Input 1

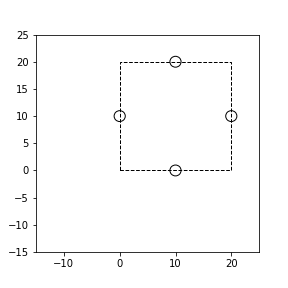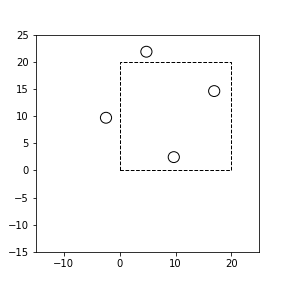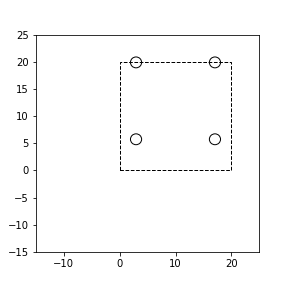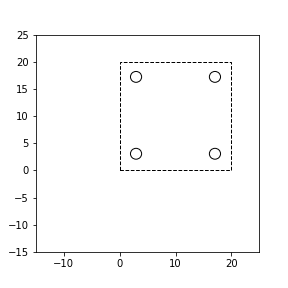
4 20 20 1
10 0
20 10
10 20
0 10

Output for Sample Input 1

Yes

All the points can be placed in the laboratory by rotating them through $45$ degrees.

Sample Input 2

2 5 55 1
0 0
30 40

Output for Sample Input 2

Yes

Sample Input 3

2 5 49 1
0 0
30 40

Output for Sample Input 3

No

Sample Input 4

1 3 3 1
114 514

Output for Sample Input 4

Yes

Problem Statement

Japanese Animal Girl Library (JAG Library) is famous for a long bookshelf. It contains $N$ books numbered from $1$ to $N$ from left to right. The weight of the $i$-th book is $w_i$.

One day, naughty Fox Jiro shuffled the order of the books on the shelf! The order has become a permutation $b_1, \ldots, b_N$ from left to right. Fox Hanako, a librarian of JAG Library, must restore the original order. She can rearrange a permutation of books $p_1, \cdots, p_N$ by performing either operation A or operation B described below, with arbitrary two integers $l$ and $r$ such that $1 \le l < r \le N$ holds.

Operation A:

• A-1. Remove $p_l$ from the shelf.
• A-2. Shift books between $p_{l+1}$ and $p_r$ to left.
• A-3. Insert $p_l$ into the right of $p_r$.

Operation B:

• B-1. Remove $p_r$ from the shelf.
• B-2. Shift books between $p_l$ and $p_{r-1}$ to right.
• B-3. Insert $p_r$ into the left of $p_l$.

This picture illustrates the orders of the books before and after applying operation A and B for $p=(3,1,4,5,2,6)$, $l=2$, $r=5$.

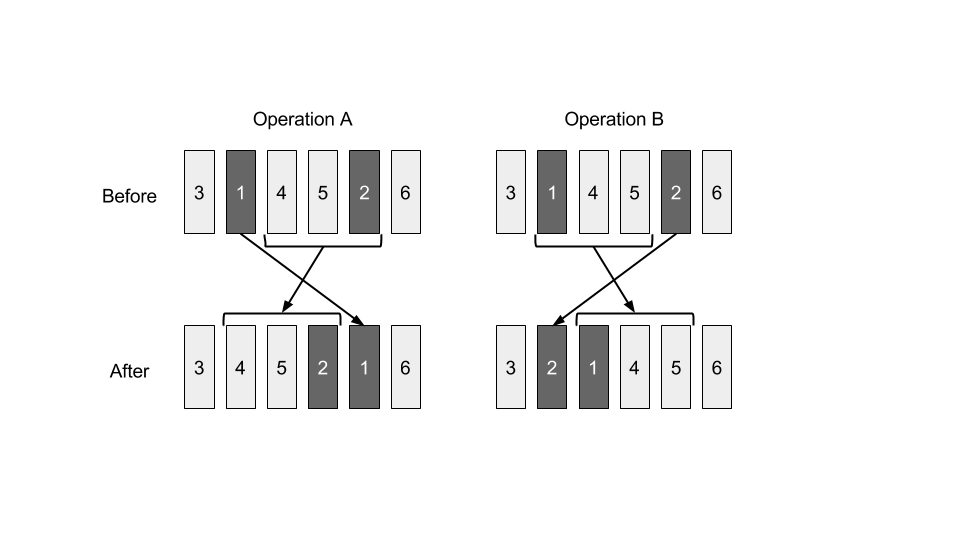
Since the books are heavy, operation A needs $\sum_{i=l+1}^{r} w_{p_i} + C \times (r-l) \times w_{p_l}$ units of labor and operation B needs $\sum_{i=l}^{r-1} w_{p_i} + C \times (r-l) \times w_{p_r}$ units of labor, where $C$ is a given constant positive integer.

Hanako must restore the initial order from $b_1, \cdots, b_N$ by performing these operations repeatedly. Find the minimum sum of labor to achieve it.

Input

The input consists of a single test case formatted as follows.

$N \ C$ $b_1 \ w_{b_1}$ $\vdots$ $b_N \ w_{b_N}$

The first line conists of two integers $N$ and $C \ (1 \le N \le 10^5, 1 \le C \le 100)$. The $(i+1)$-th line consists of two integers $b_i$ and $w_{b_i} \ (1 \le b_i \le N, 1 \le w_{b_i} \le 10^5)$. The sequence $(b_1, \ldots, b_N)$ is a permutation of $(1, \ldots, N)$.

Output

Print the minimum sum of labor in one line.

Sample Input 1

3 2
2 3
3 4
1 2

Output for Sample Input 1

15

Performing operation B with $l=1, r=3$, i.e. removing book 1 then inserting it into the left of book 2 is an optimal solution. It costs $(3 + 4) + 2 \times 2 \times 2 = 15$ units of labor.

Sample Input 2

3 2
1 2
2 3
3 3

Output for Sample Input 2

0

Sample Input 3

10 5
8 3
10 6
5 8
2 7
7 6
1 9
9 3
6 2
4 5
3 5

Output for Sample Input 3

824

Problem Statement

JAG members began a game with integers. The game consists of $N + M + 1$ players: $N$ open number holders, $M$ secret number holders, and one answerer, you.

In the preparation, an integer $K$ is told to all $N+M+1$ players. $N + M$ number holders choose their own integers per person under the following restrictions:

• Each holder owns a positive integer.
• The sum of all the integers equals $K$.
• Every integer owned by secret number holders is strictly less than any integers owned by open number holders.

After the choices, $N$ open number holders show their integers $O_{1}, \dots, O_{N}$ to the answerer while secret number holders do not.

The game has $Q$ rounds. At the beginning of each round, $M$ secret number holders can change their numbers under the above restrictions, while open number holders cannot. Then $N + M$ number holders select part of members among them arbitrary, calculate the sum $X$ of the integers owned by the selected members, and tell $X$ to the answerer. For each round, the answerer tries to identify the definitely selected open number holders from the information $K$, $X$, and $O_{1}, \dots, O_{N}$: The answerer will get points per actually selected open number holder in the answer. On the other hand, if the answer contains at least one non-selected member, you lose your points got in the round. Thus, the answerer, you, must answer only the open number holders such that the holders are definitely selected.

Your task in this problem is to write a program to determine all the open number holders whose integers are necessary to the sum for each round in order to maximize your points.

Input

The input consists of a single test case formatted as follows.

$N$ $M$ $K$ $Q$ $O_{1}$ $\cdots$ $O_{N}$ $X_{1}$ $\cdots$ $X_{Q}$

The first line consists of four integers $N$, $M$, $K$, and $Q$. $N$ and $M$ are the numbers of open number holders and secret number holders respectively $(1 \le N, 0 \le M, N + M \le 40)$. $K$ is an integer $(1 \le K \le 200{,}000)$. $Q$ is the number of rounds of the game $(1 \le Q \le 10{,}000)$.

The second line contains $N$ integers $O_{1}, \cdots, O_{N}$, as the $i$-th open number holder owns $O_{i}$ ($1 \le O_{1} \le \dots \le O_{N} \le K$).

The third line indicates $Q$ integers $X_{1}, \cdots, X_{Q}$ $(0 \le X_{i} \le K)$. $X_{i}$ is the sum of the integers owned by the selected members in the $i$-th round.

It is guaranteed that there is at least one way to compose $X_{i}$. In other words, you can assume that there is at least one integer sequence $S_{1}, \dots, S_{M}$, which represents integers owned by secret number holders, satisfying the followings:

• $0 < S_{j} < O_{1}$ for $1 \le j \le M$. Note that $O_{1} = \min_{1 \le k \le N} O_{k}$ holds.
• $\sum_{j=1}^{N} O_{j} + \sum_{k=1}^{M} S_{k} = K$.
• There is at least one pair of subsets $U \subseteq \{1, \dots, N\}$ and $V \subseteq \{1, \dots, M\}$ such that $\sum_{j \in U} O_{j} + \sum_{k \in V} S_{k} = X_{i}$ holds.

Output

On each sum $X_{i}$, print the indices of the open number holders whose integers are required to make up $X_{i}$. The output for each sum has to be printed in one line, in ascending order, and separated by a single space. If there is no open number holder whose integer is certainly used for $X_{i}$, print $-1$ in one line.

Sample Input 1

2 2 23 2
7 10
9 10

Output for Sample Input 1

1
-1

The first sum $9$ can be achieved only by the first open number holder's $7$ plus $2$ of a secret number holder. In this case, secret number holders have $2$ and $4$. The second open number holder's $10$ is a candidate for the second sum $10$. The first open holder's $7$ plus $3$ is also possible one, as secret number holders have two $3$s.

Sample Input 2

1 1 100 3
51
49 51 100

Output for Sample Input 2

-1
1
1

The only secret number holder owns $49$. The output for the first sum is $-1$ because the open number holder's $51$ is not selected.

Sample Input 3

2 1 58152 4
575 57500
575 57577 77 0

Output for Sample Input 3

1
2
-1
-1

In this case, the only secret number holder definitely has $77$. The output for the last sum $0$ is $-1$ because no integer of open number holders is needed to form $0$.

Sample Input 4

3 2 1500 1
99 300 1000
99

Output for Sample Input 4

1

The only way to compose $99$ is to select the first open number holder only; secret number holders have two integers between $1$ and $98$, while the sum of them must be $101$.

Sample Input 5

3 2 20 19
3 3 11
1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20

Output for Sample Input 5

-1
-1
-1
-1
-1
-1
1 2
1 2
1 2
3
3
3
3
3
3
3
1 2 3
1 2 3
1 2 3

The numbers owned by the two secret number holders are $1$ and $2$. At least one open number holder's $3$ is required to compose $5$ and $6$ respectively, but it is impossible to determine the definitely selected open number holder(s). On the other hand, $7$ needs the two open number holders who both own $3$.

Problem Statement

You have a permutation $p$ of $N$ integers. Initially $p_i = i$ holds for $1 \le i \le N$. For each $j \ (1 \le j \le N)$, let's denote $p^0_j = j$ and $p^k_j = p^{k-1}_{p_j}$ for any $k \ge 1$. The period of $p$ is defined as the minimum positive integer $k$ which satisfies $p^k_j = j$ for every $j \ (1 \le j \le N)$.

You are given $Q$ queries. The $i$-th query is characterized by two distinct indices $x_i$ and $y_i$. For each query, swap $p_{x_i}$ and $p_{y_i}$ and then calculate the period of updated $p$ modulo $10^9 + 7$ in the given order.

It can be proved that the period of $p$ always exists.

Input

The input consists of a single test case of the following format.

$N \ Q$ $x_1 \ y_1$ $\vdots$ $x_Q \ y_Q$

The first line consists of two integers $N$ and $Q$ ($2 \le N \le 10^5, 1 \le Q \le 10^5$). The $(i+1)$-th line consists of two integers $x_i$ and $y_i$ ($1 \le x_i, y_i \le N, x_i \ne y_i$).

Output

Print the answer in one line for each query.

Sample Input 1

5 4
2 5
2 4
1 3
1 2

Output for Sample Input 1

2
3
6
5

$p$ changes as follows: $[1,2,3,4,5] \to [1,5,3,4,2] \to [1,4,3,5,2] \to [3,4,1,5,2] \to [4,3,1,5,2]$.

Sample Input 2

2 2
1 2
1 2

Output for Sample Input 2

2
1

$p$ changes as follows: $[1,2] \to [2,1] \to [1,2]$.

Sample Input 3

10 10
5 6
5 9
8 2
1 6
8 1
7 1
2 6
8 1
7 4
8 10

Output for Sample Input 3

2
3
6
4
6
7
12
7
8
9