A - Anime Master
KM really likes Anime (Japanese animation).
He is trying to watch as many animes as possible.
The anime is broadcast at the same time zone every week.
Because he is a perfectionist, he must watch the same animes every week.
Moreover he can't watch animes which are broadcast at the same time or watch them later by recording them.
KM is a really excellent mathematician but because a lot of animes are broadcast, he couldn't find the best solution for this problem.
Can you, the excellent programmer, solve this problem?
The first line of the input file contains N and M (1 \leq N \leq 10^5, 2 \leq M \leq 10^6), which is the number of animes and the length of a week, respectively.
In KM's country, the week is composed of M unit time.
Each of the following N lines gives start time s and end time t of each animes. (0 \leq s, t < M, s \neq t)
s > t means the anime lasts over the boundary of the week.
It is possible to watch two animes whose end time is same as the other's start time.
Output the maximal number of animes he can watch.
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
He is trying to watch as many animes as possible.
The anime is broadcast at the same time zone every week.
Because he is a perfectionist, he must watch the same animes every week.
Moreover he can't watch animes which are broadcast at the same time or watch them later by recording them.
KM is a really excellent mathematician but because a lot of animes are broadcast, he couldn't find the best solution for this problem.
Can you, the excellent programmer, solve this problem?
Input
In KM's country, the week is composed of M unit time.
Each of the following N lines gives start time s and end time t of each animes. (0 \leq s, t < M, s \neq t)
s > t means the anime lasts over the boundary of the week.
It is possible to watch two animes whose end time is same as the other's start time.
Output
Sample Input
3 10 0 3 3 7 7 0
Sample Output
3
Sample Input
3 10 0 5 2 7 6 9
Sample Output
2
Sample Input
5 10 1 6 2 7 3 8 4 9 5 0
Sample Output
1
出典
The First KMCMonthly Contest
B - Cans of Toys
Chocoball is a great snack, it is not only because it tastes good, but also because you can get Cans of Toys when you are lucky.
When an angel is printed inside a package of Chocoball, you are lucky. There are two types of angels: gold angels and silver angels. You can get a Can of Toys in exchange of 1 package with a gold angel or N packages with silver angels.
It is known that a gold angel is printed in probability p and a silver angel is printed in probability q. (Two or more angels are never printed in one package.)
In addition, it is rumored that there is a rainbow angel which appears when you are really lucky. In this case, you can get K Cans of Toys at once. It is rumored that a rainbow angel is printed in probability r.
Calculate the expected number of Chocoball packages one needs to buy to get at least M Cans of Toys.
The input file contains three real numbers p, q and r (0 \leq p,q,r,p+q+r \leq 1) followed by three integers N, K (1 \leq N, K \leq 40) and M (1 \leq M \leq 10^9)
It is guaranteed that the expected value is lower than 10^{12}.
Output the expected value as a decimal fraction.
The value which is accurate to within a relative value of 1E-6 will be accepted.
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
When an angel is printed inside a package of Chocoball, you are lucky. There are two types of angels: gold angels and silver angels. You can get a Can of Toys in exchange of 1 package with a gold angel or N packages with silver angels.
It is known that a gold angel is printed in probability p and a silver angel is printed in probability q. (Two or more angels are never printed in one package.)
In addition, it is rumored that there is a rainbow angel which appears when you are really lucky. In this case, you can get K Cans of Toys at once. It is rumored that a rainbow angel is printed in probability r.
Calculate the expected number of Chocoball packages one needs to buy to get at least M Cans of Toys.
Input
It is guaranteed that the expected value is lower than 10^{12}.
Output
The value which is accurate to within a relative value of 1E-6 will be accepted.
Sample Input
0.5 0 0 1 1 1
Sample Output
2.000000
Sample Input
0.5 0.5 0 2 1 1
Sample Output
1.500000
Sample Input
0.3 0.6 0.1 2 2 2
Sample Output
2.836000
出典
The First KMCMonthly Contest
C - Containers
The land is separated into 1 \times 1 cells. Each of the containers is on one of the cells.
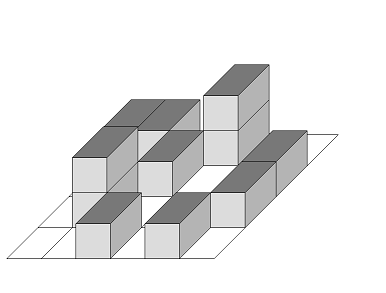
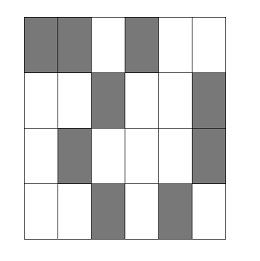
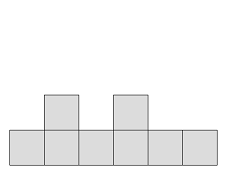
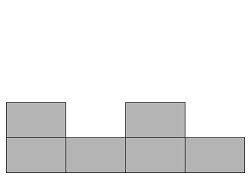 Given the photograph from the sky, front, and side respectively, calculate how many containers are piled up in the minimum.
Given the photograph from the sky, front, and side respectively, calculate how many containers are piled up in the minimum.
Each of the following H lines gives the photograph from the sky.
The value of u_{ij} means,
The next line gives the photograph from the front.
The integer f_i is the number of the containers seen in i-th row.(0 \leq f_i \leq 100)
The next line gives the photograph from the side.
The integer s_i is the number of the containers seen in i-th column.(0 \leq s_i \leq 100)
Output the minimum number of the containers.
If the photographs are inconsistent, just output
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
Some 1 \times 1 \times 1 containers are piled up in land of W \times H.The land is separated into 1 \times 1 cells. Each of the containers is on one of the cells.

Figure 1

Figure 2: from The Sky

Figure 3: from The Front

Figure 4: from The Side
Input
H W
u_{11} u_{12} … u_{1W}
u_{21} …
:
:
u_{H1} u_{H2} … u_{HW}
f_1 f_2 … f_W
s_1 s_2 … s_H
The first line of the input file contains the integers H and W (1 \leq H,W \leq 100), the number of height and width of the land.Each of the following H lines gives the photograph from the sky.
The value of u_{ij} means,
0: no containers are piled up in (i, j), 1: some containers are piled up in (i, j).The next line gives the photograph from the front.
The integer f_i is the number of the containers seen in i-th row.(0 \leq f_i \leq 100)
The next line gives the photograph from the side.
The integer s_i is the number of the containers seen in i-th column.(0 \leq s_i \leq 100)
Output
If the photographs are inconsistent, just output
-1, instead.Sample Input
2 3 0 1 0 1 1 1 2 3 2 2 3
Sample Output
9
Sample Input
4 6 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 1 0 0 1 0 1 0 1 2 1 2 1 1 2 1 2 1
Sample Output
11
出典
The First KMCMonthly Contest
D - Graph Destruction
Given a simple undirected graph with N vertices and M edges, process a sequence of K queries of two types:
The first line of the input file contains the integers N, M and K (1 \leq N, M, K \leq 10^5), separated by a space.
The next M lines describe the edges. The i-th of these lines describes edge i and it contains the integers a_i and b_i (1 \leq a_i, b_i \leq N), separated by a space. Edge i connects vertex a_i and b_i. The vertices are labeled 1 to N.
The next K lines describe the queries. Each query is either of the following two forms:
For each query of the 2nd type, print
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
- Delete an edge e
- Output whether there exists a path between vertex v and w
Input
The next M lines describe the edges. The i-th of these lines describes edge i and it contains the integers a_i and b_i (1 \leq a_i, b_i \leq N), separated by a space. Edge i connects vertex a_i and b_i. The vertices are labeled 1 to N.
The next K lines describe the queries. Each query is either of the following two forms:
0 e: delete an edge e (1 \leq e \leq M, and each edge never appears twice)1 v w: output whether there exists a path between v and w (1 \leq v, w \leq N)
Output
YES or NO, one per line, in the same order that the queries appear in the input file.
Sample Input
4 4 5 1 2 2 3 3 1 1 4 1 1 4 0 4 1 2 4 0 1 1 1 2
Sample Output
YES NO YES
出典
The First KMCMonthly Contest
E - Magic Doors
Wizard KM often forgets to close doors.
So he invented the magic door which opens with a magic spell and automatically closes after a while.
He put the doors in many places in his house, so it became very difficult to move around.
He wants to know the shortest time to move between two places in his house, so he cast a magic spell and summoned you, the excellent programmer.
KM's house consists of a matrix of square cells. A cell is one of the followings.
He can move into empty cells, start, goal, magic circles, and opened magic doors.
The house is surrounded by the walls, so he can't go out.
On a magic circle, he can cast a magic spell by consuming arbitrary amount of MP (Magic power). This takes a second. When he uses x MP, the corresponding magic doors opens during x seconds.
He can move into a door which closes at that time.
There may be more than one same magic circles or same magic doors. In this case, all the corresponding magic doors opens when he cast a magic spell on any magic circles.
At the beginning, his MP is 0. He can meditate at arbitrary timing and restore MP. Meditation takes a second per 1 MP. There is no upper bound of MP.
Find the shortest time to move from the start to the goal.
The first line of the input file contains two integers H and W (1 \leq H, W \leq 30).
Subsequent H lines of W characters \{c_{ij}\} are the map of KM's house.
Each character c_{ij} is one of the letters
There is only one start and one goal in the map.
Output the shortest time by the second.
If it is impossible to reach the goal, output
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
So he invented the magic door which opens with a magic spell and automatically closes after a while.
He put the doors in many places in his house, so it became very difficult to move around.
He wants to know the shortest time to move between two places in his house, so he cast a magic spell and summoned you, the excellent programmer.
KM's house consists of a matrix of square cells. A cell is one of the followings.
. empty # wall ^ start $ goal a-h magic circle A-H magic doorHe can move one cell to its 4-neighborhood in a second.
He can move into empty cells, start, goal, magic circles, and opened magic doors.
The house is surrounded by the walls, so he can't go out.
On a magic circle, he can cast a magic spell by consuming arbitrary amount of MP (Magic power). This takes a second. When he uses x MP, the corresponding magic doors opens during x seconds.
He can move into a door which closes at that time.
There may be more than one same magic circles or same magic doors. In this case, all the corresponding magic doors opens when he cast a magic spell on any magic circles.
At the beginning, his MP is 0. He can meditate at arbitrary timing and restore MP. Meditation takes a second per 1 MP. There is no upper bound of MP.
Find the shortest time to move from the start to the goal.
Input
Subsequent H lines of W characters \{c_{ij}\} are the map of KM's house.
Each character c_{ij} is one of the letters
., #, ^, $, a-h, A-H.There is only one start and one goal in the map.
Output
If it is impossible to reach the goal, output
-1 instead.
Sample Input
1 3 ^.$
Sample Output
2
Sample Input
1 4 ^aA$
Sample Output
5
Sample Input
1 4 ^aB$
Sample Output
-1
Sample Input
3 3 ^AB a#A b#$
Sample Output
19
出典
The First KMCMonthly Contest
F - Maximum Segment XOR
XOR is the operation as basic as addition for programmers.
Genius programmer KM made the following problem to test his disciple wata.
Given N integers \{a_i\}, find the two integers s and t (1 \leq s \leq t \leq N) such that a_s\^a_{s+1}\^…\^a_t is maximum possible.
wata couldn't solve this problem, so he asked you, the friend of him and the excellent programmer, to solve this problem for him.
The first line of the input file contains N (1 \leq N \leq 10^5).
The second line contains N integers \{a_i\} (0 \leq a_i < 2^{20}).
Output the maximal value and the pair of (s, t) which gives the maximum.
If there are multiple pairs, output the lexicographically smallest one.
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
Genius programmer KM made the following problem to test his disciple wata.
Given N integers \{a_i\}, find the two integers s and t (1 \leq s \leq t \leq N) such that a_s\^a_{s+1}\^…\^a_t is maximum possible.
wata couldn't solve this problem, so he asked you, the friend of him and the excellent programmer, to solve this problem for him.
Input
The second line contains N integers \{a_i\} (0 \leq a_i < 2^{20}).
Output
If there are multiple pairs, output the lexicographically smallest one.
Sample Input
5 1 2 3 4 5
Sample Output
7 3 4
Sample Input
3 3 3 3
Sample Output
3 1 1
Sample Input
4 1 2 4 8
Sample Output
15 1 4
出典
The First KMCMonthly Contest
G - Moving Points
You are given N points in the xy-plane. Each point is in a state of linear uniform motion.
Your task is to calculate the distance to the furthest point in Manhattan distance from the origin at time t.
The first line of the input file contains the integers N and M (1 \leq N, M \leq 10^5), separated by a space.
The next N lines describe the points. Each contains four real numbers x, y, vx and vy (|x|,|y|,|vx|,|vy| \leq 10^6). This shows the initial coordinates (x, y) and velocity (vx, vy).
The next M lines describe the queries. Each line contains one real number t (0 \leq t \leq 10^6).
For each query, output the maximal Manhattan distance in one line.
The value which is accurate to within a relative or absolute value of 1E-9 will be accepted.
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
Your task is to calculate the distance to the furthest point in Manhattan distance from the origin at time t.
Input
The next N lines describe the points. Each contains four real numbers x, y, vx and vy (|x|,|y|,|vx|,|vy| \leq 10^6). This shows the initial coordinates (x, y) and velocity (vx, vy).
The next M lines describe the queries. Each line contains one real number t (0 \leq t \leq 10^6).
Output
The value which is accurate to within a relative or absolute value of 1E-9 will be accepted.
Sample Input
2 2 0 0 1 0 1 0 -1 0 0 1
Sample Output
1.0000000000 1.0000000000
Sample Input
3 3 0 0 1 1 0 1 1 0 3 3 -2 -1 0 1 2
Sample Output
6.0000000000 3.0000000000 4.0000000000
Sample Input
3 3 1 1 0.5 0 0 2 1.5 -1 1.5 0 0 1 0 1 2
Sample Output
2.0000000000 2.5000000000 3.5000000000
出典
The First KMCMonthly Contest
H - Shuffling Machine
KM bought a new card shuffling machine.
According to his hypothesis, everytime you setup N cards and push the switch, it shuffles the cards in a totally same way. More precisely, there exists a sequence of integers a_1, a_2, ..., a_N such that
He wanted to know this sequence, so he setup N cards in the ascending order: 1, 2, ..., N. However, he accidentally pushed the switch K times, and the resulting order of the cards was b_1, b_2, ..., b_N.
But KM says that you can guess a_1, a_2, ..., a_N from b_1, b_2, ..., b_N. Can you do that?
The first line of the input file contains the integers N (1 \leq N \leq 10^5) and K (1 \leq K \leq 10^{18}), separated by a space.
The second line of the input file contains N different integers which denotes b_1, b_2, ..., b_N (1 \leq b_i \leq N) in this order, separated by a space.
If KM's hypothesis seems to be wrong, just print
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
According to his hypothesis, everytime you setup N cards and push the switch, it shuffles the cards in a totally same way. More precisely, there exists a sequence of integers a_1, a_2, ..., a_N such that
- the 1st card in the resulting order is always the a_1-th card in the initial order,
- the 2nd card in the resulting order is always the a_2-th card in the initial order,
- ..., and so on.
He wanted to know this sequence, so he setup N cards in the ascending order: 1, 2, ..., N. However, he accidentally pushed the switch K times, and the resulting order of the cards was b_1, b_2, ..., b_N.
But KM says that you can guess a_1, a_2, ..., a_N from b_1, b_2, ..., b_N. Can you do that?
Input
The second line of the input file contains N different integers which denotes b_1, b_2, ..., b_N (1 \leq b_i \leq N) in this order, separated by a space.
Output
Impossible. If there are several possibilities, print Ambiguous. Otherwise, print N integers which denotes a_1, a_2, ..., a_N in this order, separated by a space.
Sample Input
3 2 3 1 2
Sample Output
2 3 1
Sample Input
3 2 1 3 2
Sample Output
Impossible
Sample Input
4 2 2 1 4 3
Sample Output
Ambiguous
出典
The First KMCMonthly Contest
I - Topology
KM discovered that the number of holes is very important for some geometrical problems. He wants to calculate the number of holes of various figures. To simplify this problem, he assumes that the figures are composed of some unit squares whose vertices are on lattice points.
He can calculate it when the number of the squares is small. He can't calculate it by hand when the number is large, so he asks you, the friend of him and the excellent programmer, to solve this problem by computers.
 A hole is a bounded connected component when all squares are removed. When two components share some edges, they are considered connected.
A hole is a bounded connected component when all squares are removed. When two components share some edges, they are considered connected.
The first line of the input file contains N (1 \leq N \leq 10^5), which is the number of squares.
Each of the following N lines describes a square by specifying integers X and Y (|X|, |Y| \leq 10^9) separated by single blank characters. X and Y are coordinates of the lower left corner.
You can assume that any two coordinates are different.
Output the number of the holes that the figure has.
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
He can calculate it when the number of the squares is small. He can't calculate it by hand when the number is large, so he asks you, the friend of him and the excellent programmer, to solve this problem by computers.

Figure 1: Holes
Input
Each of the following N lines describes a square by specifying integers X and Y (|X|, |Y| \leq 10^9) separated by single blank characters. X and Y are coordinates of the lower left corner.
You can assume that any two coordinates are different.
Output
Sample Input
4 0 0 1 -1 2 0 1 1
Sample Output
1
Sample Input
16 1 0 3 0 5 0 0 1 2 1 4 1 1 2 3 2 4 2 1 3 5 3 0 4 1 4 2 4 4 4 3 5
Sample Output
3
出典
The First KMCMonthly Contest
J - Very Intellectual Card Game
Alice and Bob decide to play a new card game using a deck with N cards. N is even. Each card has a number between -10^9 to 10^9.
Bob shuffles the deck M times. In the i-th time, he swaps the [1, k_i)-th cards and [k_i, n]-th cards counting from the top of the deck.
For example, when the deck is <1, 2, 3, 4, 5, 6> and k_i equals 4, the deck becomes <4, 5, 6, 1, 2, 3> after shuffle.
Alice can stop his shuffle after arbitrary times, of course 0 times also. (He does not shuffle after she stopped his shuffle.)
When she stops shuffle or he ends shuffle M times, Alice gets the upper half of the deck. When does the sum of the cards she gets become maximum?
The first line of the input file contains N and M (2 \leq N \leq 10^5, 1 \leq M \leq 10^5), which is the number of cards and shuffles. N is even.
The second line contains N integers that are written on the cards from the top of the deck. The integers are between -10^9 and 10^9 inclusive.
The third line contains M integers \{k_i\} (2 \leq k_i \leq N).
Output the maximal sum of the cards that Alice can get.
実行時間制限: 1.5 sec / メモリ制限: 93 MiB
Description
Bob shuffles the deck M times. In the i-th time, he swaps the [1, k_i)-th cards and [k_i, n]-th cards counting from the top of the deck.
For example, when the deck is <1, 2, 3, 4, 5, 6> and k_i equals 4, the deck becomes <4, 5, 6, 1, 2, 3> after shuffle.
Alice can stop his shuffle after arbitrary times, of course 0 times also. (He does not shuffle after she stopped his shuffle.)
When she stops shuffle or he ends shuffle M times, Alice gets the upper half of the deck. When does the sum of the cards she gets become maximum?
Input
The second line contains N integers that are written on the cards from the top of the deck. The integers are between -10^9 and 10^9 inclusive.
The third line contains M integers \{k_i\} (2 \leq k_i \leq N).
Output
Sample Input
10 5 1 -3 2 2 -4 1 1 5 -2 -2 2 8 5 8 10
Sample Output
2