Time Limit: 1 sec / Memory Limit: 256 MB
問題文
あなたは机の上で大きな長方形のウエハースを1段2段とらせん状に積み重ねて遊んでいました。
最初のウエハースは好きなように置き、それ以降のウエハースは最高段のウエハースと一方の対角線が一致するように回転してその上に置きます。
例として、以下の図では1段目に白のウエハース、2段目に青いウエハースが配置されています。
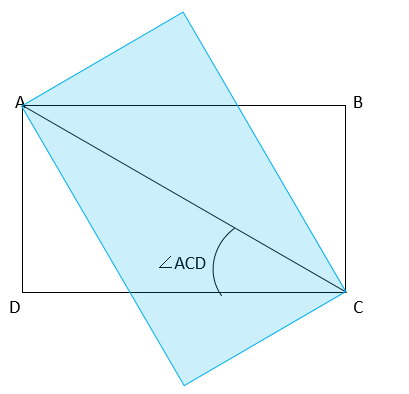
あなたはウエハースを置く時にすでに置いたいずれかのウエハースと完全に重なってしまう可能性があることに気付きました。 それは美しくないので、あなたはウエハースが上から見たときに完全に重なることなくウエハースを最大何段まで積められるか調べることにしました。
また、あなたは分度器しか持っていないのでウエハースの大きさはわからず、代わりに対角線と辺がなす角度が与えられます。
入力
入力は以下の形式で標準入力から与えられる。
∠ACD
- 1行目には、ACDの角度を示す整数(13:45追記)∠ACD(1≦∠ACD≦89)が度数法で与えられる。（1度なら1、45度なら45が入力である。）
配点
この問題の配点は100点であり、部分点はない。
出力
積み重ねることのできるウエハースの数を出力せよ。出力の末尾に改行を入れること。
ウエハースを限りなく積むことができる場合は-1を返すこと。
入力例1
30
出力例1
3
4つ目のウエハースは1つ目のウエハースと完全に重なってしまうので置くことができない。
入力例2
18
出力例2
5
入力例3
45
出力例3
1
ウエハースが正方形である場合に注意せよ。
Time Limit: 5 sec / Memory Limit: 256 MB
問題文
すぬけ君はすめけさんと二人で数の書かれたカードとコインを使って以下のようなゲームをすることにしました。
はじめ、すぬけ君は T が書かれたカード一枚と K 枚のコインを、すめけさんはカードを N 枚持っている。
このゲームは N 回のラウンドに分かれていて、すめけさんは各ラウンドでは以下の手順を一回行う。
- すめけさんはまだすぬけ君に見せていないカードを一枚選び、それをすぬけ君に見せる。このカードに書かれている数字を A とする。
- すぬけ君の持っているカードに書かれた数字を B とすると、すぬけ君はすめけさんから|A-B| ダメージを受ける。
- すぬけ君はコインを持っているとき、すめけさんにコインを一枚渡して A のカードを B のカードと交換するか、コインを渡さずに何もしないかのどちらかを行う。
そこで、すぬけ君はすめけさんの作戦を探り出し、すめけさんはすぬけ君の行動に関わらず i 回目に書かれている値が A_i のカードを出すのだと確信した。
すぬけ君が各ラウンドで受けるダメージの最大値として考えられる最小の値を求めてくさだい。
ただし、各ラウンドが終わった後、すぬけ君のダメージはすめけさんによって回復されることとする。
入力
入力は以下の形式で標準入力から与えられる。
N T K A_1 A_2 ... A_N
- 一行目にはラウンドの数 N(1≦N≦100,000)とすぬけ君が最初に持っているカードに書かれている数 T(1≦T≦10^{9})、コインの枚数 K(1≦K≦N) が与えられる。
- 次の行にはN 個の数が与えられ、i 個目の整数としてすめけさんが i(1≦i≦N) 回目に出すカードに書かれている数 A_{i}(1≦A_{i}≦10^{9}) が与えられる。
配点
この問題には部分点があります。追加制約として、 N=K を満たす場合についてこの問題を解くと20点が与えられます。
出力
すぬけ君が各ラウンドで受けるダメージの最大値として考えられる最小の値を一行に出力せよ。 末尾には改行を入れること。入力例1
5 1 1 1 2 3 4 5
出力例1
2
入力例2
8 9 3 11 4 5 14 19 19 8 10
出力例2
6
Time Limit: 3 sec / Memory Limit: 256 MB
問題文
石油王となったすぬけ君はガソリンをこよなく愛していて、王国内の移動には車を欠かさず使う。
王国にはN個のガソリンスタンドがあり、i 個目のガソリンスタンドではガソリンが 1 Lあたり V_i 円で売っている。
また、ガソリンスタンドは 1 番目から N 番目まで一直線上に並んでおり、i 個目とj 個目のガソリンスタンドを移動するのには|i-j| Lのガソリンが必要である。
さて、すぬけ君は Q 日間のガソリンスタンドめぐりを計画している。
i 日目には S_i 番目から T_i 番目のガソリンスタンドに行こうとしている。そのために、いくつかのガソリンスタンドを経由していくことになるであろうが、ガソリンスタンドに止まるたびにそこが目的地であってもお金を払って車に満タンまでガソリンを入れる。また、目的地には必ず止まらなければならないが、その途中の経路にあるガソリンスタンドには必ずしも止まる必要はなく、止まるガソリンスタンドは運転手が自由に選ぶことができる。
すぬけ君の運転手のすめけさんはすぬけ君が給油をするのは止めることはできないので、どこのガソリンスタンドに止まっていけば最も安く目的のガソリンスタンド間の移動ができるのかを調べることにしました。
そこで、あなたの出番です。各日程で、すぬけさんが使うお金の最小値を求めてください。
ただし、毎日の旅の前には車にはガソリンが満タン入っていることが保障されており、 いかなるガソリンスタンド間の移動でもすぬけ君の車からガソリンがなくなることはない。
入力
入力は以下の形式で標準入力から与えられる。
N Q V_1 V_2 ... V_N S_1 T_1 S_2 T_2 ... S_Q T_Q
- 一行目にはガソリンスタンドの個数 N(1≦N≦4000) とすぬけ君の旅の日数 Q(1≦Q≦200,000) が与えられる。
- 次の行では整数が N 個与えられ、i 番目の整数として、 i 番目のガソリンスタンドでの 1 Lあたりのガソリンの値段 V_{i}(1≦V_{i}≦100,000) が与えられる。
- 続く Q 行のうちの i 行目には i(1≦i≦Q) 日目にすぬけ君がスタートするガソリンスタンド S_{i}(1≦S_{i}≦N) とゴールであるガソリンスタンド T_{i}(1≦T_{i}≦N) が空白区切りで与えられる。このとき、S_{i}≠T_{i} であることが保障されている。
配点
この問題には部分点はない。
出力
i(1≦i≦Q) 行目に i 日目の移動にかかるお金の最小値を出力せよ。
入力例1
3 3 5 3 4 3 1 1 2 2 1
出力例1
8 3 5
入力例2
5 5 9 5 10 6 6 5 1 2 1 2 3 1 4 1 4
出力例2
24 9 10 17 17
入力例3
6 1 100 100 100 5 3 1 1 4
出力例3
13
遠回りをしていく方がよい場合もあることに注意せよ。
Time Limit: 3 sec / Memory Limit: 256 MB
問題文
すぬけ君はN個の駅からなる国に住んでいる。この国では、A 社と B 社の鉄道会社だけがあり、それぞれが独自に線路を作っている。
これらの線路は二つの駅間を結んでおり、各線路には長さがある。どちらの鉄道会社も二つの駅の間を自社の線路だけを使って同じ線路を 2 回以上使わずに行く。このとき、どの二つの駅に対しても、そのような経路がそれぞれちょうど一通りずつあることが分かっている。
そこで、どちらの会社も自分の会社の作った線路の性質を生かして、i 番目の駅と j 番目の駅間の移動料金をその間を移動するときに通る隣り合った駅の間の距離の最大値としています。
すぬけ君は相異なる 2 駅間の移動に対して、どちらの鉄道会社を使った方がいいのか考えていました。そこで、何個かの相異なる駅間の移動ではどちらの鉄道会社を使っても料金が同じなのではないかと思い、そのような駅の組の数を求めようと思いました。
さて、いったい何通りの駅の組が料金が 2 社とも同じであったでしょうか。
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 b_1 p_1
a_2 b_2 p_2
...
a_{N-1} b_{N-1} p_{N-1}
c_1 d_1 q_1
c_2 d_2 q_2
...
c_{N-1} d_{N-1} q_{N-1}
- 一行目は駅の数 N(1≦N≦100000) を表している。
- 続く N-1 行は A 社が作った線路の情報を表しており、a_{i}(1≦a_{i}≦N) 番目の駅と b_{i}(1≦b_{i}≦N) 番目の駅を結ぶ長さ p_{i}(1≦p_{i}≦10^{9}) の線路を A 社が作ったことを表している。
- 続く N-1 行は B 社が作った線路の情報を表しており、c_{i}(1≦c_{i}≦N) 番目の駅と d_{i}(1≦d_{i}≦N) 番目の駅を結ぶ長さ q_{i}(1≦q_{i}≦10^{9}) の線路を B 社が作ったことを表している。
配点
この問題には部分点がある。以下の制約を追加で満たすデータセットに正解した場合は 40 点が与えられる。
- 同じ鉄道会社は同じ長さの線路を作らない。
出力
どちらの鉄道会社を使っても料金が変わらないような駅の組の数を一行に出力せよ。改行を忘れないこと。
入力例1
5 1 2 5 1 3 1 4 3 3 5 2 3 1 2 2 5 1 2 1 3 3 2 4 2
出力例1
1
入力例2
5 5 3 1 2 4 3 1 2 2 2 3 1 1 3 1 5 4 3 4 2 2 4 3 1
出力例2
2
入力例3
5 3 2 5 5 2 4 2 4 1 1 2 2 2 5 4 3 2 5 4 2 1 2 1 2
出力例3
10これは部分点の制約を満たす。
Time Limit: 4 sec / Memory Limit: 256 MB
問題文
誕生日プレゼントにすぬけ君は待望の自動MOD取り機をお母さんからもらいました。
この自動MOD取り機は N 個の変数 A_{1}～A_{N} の値を表示する機械であり、すぬけ君はこの機械にあるコマンドをいじくることで遊んでいましたが、興奮して使いすぎてしまったので自動MOD取り機は変な挙動をし始めてしまいました。
本来の自動MOD取り機は以下のようなコマンドがあります。
| セット | これを実行すると、A_1～A_N の値を0にする。 |
| コマンド1 | p,v の値を入力する。このコマンドがセットしてからi回目のコマンドの時、A_1～A_pの中で、i+vで割った余りがi以上の値のものをすべて、 その数より大きい最小のi+vの倍数に置き換える。 |
| コマンド2 | p の値を入力する。このコマンドでは A_p の値を出力する。 |
| コマンド3 | v の値を入力する。このコマンドでは A_1～A_n すべてにvを加える。 |
すぬけ君はしょうがないのでこのコマンドに答えるプログラムを組もうとしました。 しかし、なかなかうまくいかないので、助けてください。
ただし、すぬけ君は最初にセットをした後はセットコマンドは実行せず、入力として与えられるのは最初に行われるセットコマンド以外が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N Q （1個目のコマンド） （2個目のコマンド） . . . （Q個目のコマンド）
- 一行目には配列の数 N(1≦N≦100,000) とすぬけ君がセットコマンドを行った後に実行するコマンドの数 Q(1≦Q≦100,000) が与えられる。
- 続く Q 行の内の i(1≦i≦Q) 行目にはすぬけ君がセットコマンドを実行してから i 回目のコマンドが与えられる。
これらは以下のいずれかである。
1 p v
これは、コマンド1 の入力として、p,v が入力で与えられることを表す。これらは、1≦p≦n,1≦v≦10 を満たす。2 p
これは、コマンド2 の入力として、p が入力で与えられることを表す。これは、1≦p≦n を満たす。3 v
これは、コマンド3 の入力として、v が入力で与えられることを表す。これは、1≦v≦100,000 を満たす。
配点
この問題には部分点がない。
出力
i 回目のコマンド2 に対する出力を i 行目に出力せよ。
入力例1
5 7 3 5 2 3 1 3 10 2 3 1 4 10 2 3 2 4
出力例1
5 13 15 15
A_{i} の値は以下のように変更される。
[A_{1},A_{2},A_{3},A_{4},A_{5}] : [0,0,0,0,0]→[5,5,5,5,5]→[13,13,13,5,5]→[15,15,15,15,5]
入力例2
3 6 2 1 3 9 1 3 3 2 1 1 1 1 2 1
出力例2
0 12 12