Time Limit: 0 msec / Memory Limit: 256 MiB
かつて豊かな森林だったある地は人間たちによって荒らされてしまい、そこで暮らしていたどうぶつたちも姿を消しました。これはその少し後の話です。
これまで好き放題していた人間たちは、ようやく地球のあげる悲鳴に気がつきました。人間たちは過去の行いを悔い、環境を守り失われた森林を再生する活動を始めました。
きつねの次郎たちが暮らしていた場所にも少しずつではありますが緑が帰ってきました。次郎とその仲間のどうぶつたちは、暮らし慣れた場所でもう一度楽しく過ごしたいと思ってその場所へ帰ってきました。
新しく再生された森林にもどうぶつたちの遊び場があります。どうぶつたちは遊び場を結ぶ道をもう一度作りなおして、遊び場どうしの行き来ができるようにしようと思いましたが、新しい森林にはまだ慣れきっていないのでできるだけシンプルな道を作ることにしました。
具体的には、どの遊び場からどの遊び場へもちょうど 1 通りの経路があるようにします。こうすれば新しい森でも迷う心配なく遊び場へと行くことができます。そのような道の作り方はきっとたくさんあるので、その中で道の長さの合計がいちばん小さくなるようにしましょう。
どうぶつたちが新しい森で快適に過ごすための手伝いをしてもらえないでしょうか。
課題
はじめ 1 つの頂点のみからなるグラフに頂点と辺と追加していき、最終的には頂点の数を N 個にする。最初からある頂点には番号 0 がつけられており、頂点 i の直後に追加される頂点には番号 i+1 がつけられる。
次のプロシージャを実装せよ:
- 次のパラメータを持つプロシージャ construct(N, M, E):
- N -- 頂点の数。各頂点は、追加される順に0からN-1まで番号がつけられている。
- M -- 使用可能な辺の数。
- E -- 使用可能な辺の情報を表す 2 次元配列. 0 ≦ i < M に対し, 辺 i は頂点 E[i][0] と E[i][1] を結んでいて、その長さはE[i][2]である。0 ≦ E[i][0] < E[i][1] < N, 1 ≦ E[i][2] ≦ 1 000 000 000を仮定してよい。
例
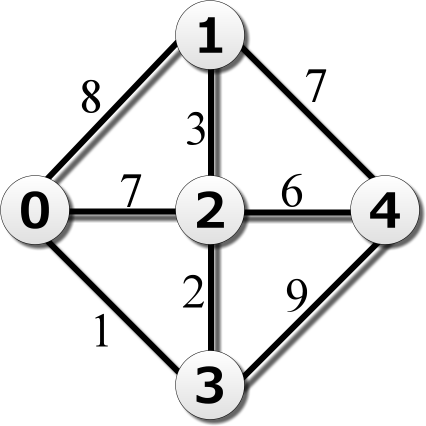
図 1
図1に示される N = 5, M = 8,
| E = | 0 | 1 | 8 | ||
| 0 | 2 | 7 | |||
| 0 | 3 | 1 | |||
| 1 | 2 | 3 | |||
| 1 | 4 | 7 | |||
| 2 | 3 | 2 | |||
| 2 | 4 | 6 | |||
| 3 | 4 | 9 |
の場合を考える。この場合、constructはanswerを4回呼ばなければならない。以下に正しいanswerの呼び出し方法を示す:
| 回数(x) | 呼び出し |
|---|---|
| 1 | answer(8) |
| 2 | answer(10) |
| 3 | answer(6) |
| 4 | answer(12) |
小課題
以下、1回の実行における construct 呼び出しのパラメータ P の総和、すなわち最終的にできあがるグラフの辺の数を M とする。
小課題 1 (16 点)
- 1 ≦ N ≦ 1 000
- 0 ≦ M ≦ 2 000
小課題 2 (24 点)
- 1 ≦ N ≦ 5 000
- 0 ≦ M ≦ 60 000
小課題 3 (59 点)
- 1 ≦ N ≦ 20 000
- 0 ≦ M ≦ 60 000
小課題 4 (1 点)
- 1 ≦ N ≦ 100 000
- 0 ≦ M ≦ 200 000
実装の詳細
制限
- CPU 時間制限: 1.5 秒
- メモリ制限: 256 MB
注意: スタックのサイズには決められた制限はない。スタックとして使用されたメモリは、メモリ総使用量に含まれる。
インターフェース (API)
- 実装フォルダ: animals2/ (プロトタイプ: animals2.zip)
- 競技者が実装するファイル: animals2.cpp
- 提出ファイルのインターフェース: animals2.h
- 採点プログラムのサンプル: grader.cpp
- 採点プログラムの入力のサンプル: grader.in.1, grader.in.2, ...
注意:採点プログラムのサンプルは次の書式の入力を読み込む。- 1 行目: N, M が空白区切りで書かれている。
- 2 行目から M+1 行目: 0 ≦ i < M に対し、i+2 行目には 3 つの整数 E[i][0], E[i][1], E[i][2] が空白区切りで書かれている。
- 採点プログラムの入力のサンプルに対して期待される出力: grader.expect.1, grader.expect.2, ...
注意:採点プログラムのサンプルは次の書式の出力を書き出す。- 1 行目から N-1 行目: 0 ≦ i < N-1 に対し、i+1 行目には constructがi 回目に answer を呼び出したときの戻り値が書かれている。
Time Limit: 0 msec / Memory Limit: 256 MiB
きつねの次郎のすむ森には一匹のおばけが住んでいます。 お化けはいたずらが大好きで、いつも次郎やその仲間のどうぶつたちをいたずらで驚かせて楽しんでいます。 ですが、おばけのいたずらは楽しいいたずらで、どうぶつたちをいやがらせることはありません。 また、森の外のおばけとは違い、このおばけは怖い人間に化けたりもしません。 なので、次郎たちどうぶつはこのやさしいおばけが大好きです。
ある日、次郎たちはおばけの誕生日会を開きました。 次郎たちの用意したバースデーケーキには、おばけの年齢である N 本の火が灯ったろうそくが立っています。 しかし、招待されたおばけはまた楽しいいたずらを思いつき、次郎たちを驚かせようと透明に化けてしまいました。 次郎たちは今日の主役であるおばけが見えなくなって困ってしまったのですが、とある事に気がつきました。 おばけは透明になって見えないのに、ろうそくの光でおばけの影が壁に映っているのです! 次郎たちは、この影によっておばけがどこに居るのか分からないだろうかと考えました。 バースデーケーキはとても大きいので、おばけ、ろうそく、おばけの影は点と考える事ができます。
課題
xyz空間中に、1匹のおばけとN個のろうそくがある。 おばけは地点G(Gx,Gy,Gz)に居て、 i番目のろうそくの火は地点Ci(Cx[i],Cy[i],Cz[i])に灯っている。 また、各iについて、0<Gx<Cx[i]が満たされている。 yz平面(x=0で表される平面)には壁があり、各iについて、GとCiを結んだ直線と壁の交点に影Si(0,Syi,Szi)が映っている。
次のプロシージャを実装せよ:
-
次のパラメータを持つプロシージャ FindGhost(N,Cx,Cy,Cz,Ty,Tz):
- N -- ろうそくの本数。
- Cx -- ろうそくの火のx座標を表す実数の配列。0≤i<Nに対して0≤Cx[i]≤1を仮定してよい。
- Cy -- ろうそくの火のy座標を表す実数の配列。0≤i<Nに対して0≤Cy[i]≤1を仮定してよい。
- Cz -- ろうそくの火のz座標を表す実数の配列。0≤i<Nに対して0≤Cz[i]≤1を仮定してよい。
- Ty -- 影のy座標を表す実数の配列。0≤i<Nに対して0≤Ty[i]≤1を仮定してよい。
- Tz -- 影のz座標を表す実数の配列。0≤i<Nに対して0≤Tz[i]≤1を仮定してよい。
例
N=3 Cx={0.9,0.45,0.6} Cy={0.8,0.2,0.1} Cz={0.5,0.4,0.8} Ty={0.7,0.2,0.8} Tz={0.2,0.5,0.7} の場合を考える。
このとき各点は下図の位置にある。
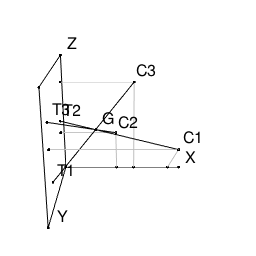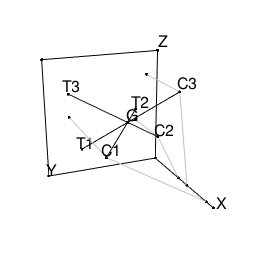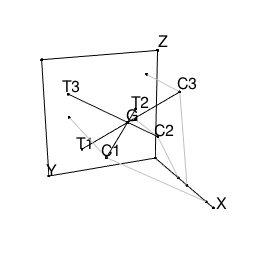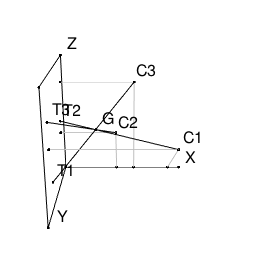 G(0.3,0.4,0.5)を考えると、
C1の影S1がT2、
C2の影S2がT3、
C3の影S3がT1
であることが分かるので、このGがおばけのいる場所である。
よってFindGhostはanswer(0.3,0.4,0.5)を呼び出す。
G(0.3,0.4,0.5)を考えると、
C1の影S1がT2、
C2の影S2がT3、
C3の影S3がT1
であることが分かるので、このGがおばけのいる場所である。
よってFindGhostはanswer(0.3,0.4,0.5)を呼び出す。
小課題
小課題 1 (19 点)
- 1≤N≤10
小課題 2 (40 点)
- 1≤N≤100000
- 0≤i<Nについて、Cz[i]=0,Tz[i]=0である。
小課題 3 (41 点)
- 1≤N≤100000
実装の詳細
制限
- CPU 時間制限: 1秒
- メモリ制限: 256 MB
注意: スタックのサイズには決められた制限はない。スタックとして使用されたメモリは、メモリ総使用量に含まれる。
インターフェース (API)
- 実装フォルダ: ghost/ (プロトタイプ: ghost.zip)
- 競技者が実装するファイル: ghost.cpp
- 提出ファイルのインターフェース: ghost.h
- 採点プログラムのサンプル: grader.cpp
- 採点プログラムの入力のサンプル: grader.in.1, grader.in.2, ...
注意:採点プログラムのサンプルは次の書式の入力を読み込む。- 1 行目: 整数Nが書かれている。Nはろうそくの数を表す。
- 2 行目から 1+N 行目: 1 ≤ i ≤ N に対し、i+1行目には実数Cx,Cy,Czが書かれている。これらはそれぞれろうそくCiのx,y,z座標を表す。
- 2+N 行目から 1+2N 行目: 1 ≤ i ≤ N に対し、i+N+1行目には実数Ty,Tzが書かれている。これらはそれぞれ影Tiのy,z座標を表す。
- 採点プログラムの入力のサンプルに対して期待される出力: grader.expect.1, grader.expect.2, ...
注意:採点プログラムのサンプルは次の書式の出力を書き出す。- 1行目:実数Gx,Gy,Gzが書かれている。これらはそれぞれおばけのいる地点Gのx,y,z座標を表す。
Time Limit: 0 msec / Memory Limit: 256 MiB
きつねの次郎は旅するきつねです。ある日次郎が歩いて旅をしていると分かれ道にさしかかりました。
片方の道の先には「うそつき村」があって、そこには嘘ばかり言う悪い人間がたくさんいます。もう片方の道の先「しょうじき村」があって、そこには嘘を決してつかない優しいきつねがたくさんいます。
次郎はとうぜん「しょうじき村」へ行きたいのですが、残念なことに分かれ道には標識がありません。きっと悪い人間がいじわるをしているのでしょう。
その道の周辺には N 人の人間がいるようです。そのうちの何人かは「うそつき村」から来た悪い人間です。他の人間はじつは「しょうじき村」から来た優しいきつねで、悪い人間にいじわるをされないように人間に化けています。
見た目からではある人間が「しょうじき村」から来たきつねなのか「うそつき村」から来た人間なのかは区別できません。次郎はその N 人に対して質問をすることで「しょうじき村」から来たきつねをすべて特定したいと思っています。
あまりたくさん質問をするのは時間がかかってしまうし、次郎も頭がこんがらがってしまいます。次郎がちゃんと「しょうじき村」へ行けるように、質問するのを手伝ってもらえないでしょうか。
課題
N 人の人間がおり、0 から N-1 までの異なる整数の番号がつけられている。それぞれの人間は正直か嘘つきのどちらかであり、次の 2 種類の質問を繰り返すことで正直者をすべて特定したい。
- ある人 i に対して「人 j は正直者ですか?」と質問する
- ある人 i に対して「N 人のうち正直者は何人いますか?」と質問する
次のパラメータをもつプロシージャ identify(N) を実装せよ:
- N -- 人の数。人には 0 から N-1 までの異なる整数の番号がつけられている。
identify(N) 中では question(Q, i, j) を繰り返し呼び出すことができる。question(Q, i, j) の仕様は次の通り:
- Q=1 のとき question(Q, i, j) は人 i に対して「人 j は正直者ですか?」と質問したときの返答を返す。戻り値は Yes を表す 1 か No を表す 0 のいずれかである。
- Q=2 のとき question(Q, i, j) は人 i に対して「N 人のうち正直者は何人いますか?」と質問したときの返答を返す。戻り値は 0 以上 N 以下の整数である。このとき j の値は内部で捨てられるので何を指定しても構わない。
- それ以外の Q の値で question(Q, i, j) を呼び出すと不正なライブラリ呼び出しとみなし、不正解と判定する。
質問に対し、正直者は常に正しい答を返し嘘つきは常に間違った答を返す。嘘つきの返答は間違いであればどのようなものでもありうるが、同じ質問を繰り返した際には同じ答を返すことは保証されている。
質問を繰り返し、それぞれの人 i についてその人が正直者であるか嘘つきであるかを判定し answer(i, X) を呼び出せ。X は人 i が正直者であることを表す 1 か嘘つきであることを表す 0 のいずれかである。answer(i, X) はどのような i の順番で呼び出しても構わないが、すべての人についてちょうど1回ずつ呼び出される必要がある。
ただしどのように質問をしても正直者をすべて特定できない場合がある。そのような場合には identify(N) は answer(i, X) を一度も呼び出さず、かわりに impossible() を呼び出して終了する必要がある。identify(N) は戻り値を持たない。
なお question(Q, i, j) は矛盾した答を返さないことが保証されている。すなわち question(Q, i, j) の結果をすべて満たすような正直者の組み合わせが少なくとも1通り存在する。
例
例1
N = 2 の場合を考える。question を次のようなパラメータで呼び出し、以下に示すような返答を得たとする。
| パラメータ | 戻り値 |
|---|---|
| question(1, 0, 1) | 0 |
| question(2, 1, -1) | 0 |
これは人 0 は「人 1 は正直者ですか?」という質問に No と返答し、人 1 は「2 人のうち正直者は何人いますか?」という質問に 0 人と返答したことを表す。
人 1 が正直者だと仮定すると正直者は少なくとも 1 人はおり、これは質問の答と矛盾するので人 1 は嘘つきである。いっぽう人 0 は人 1 について正しい返答をしているので正直者である。したがって identify は次のような answer 呼び出しを行う必要がある。
| パラメータ |
|---|
| answer(0, 1) |
| answer(1, 0) |
例2
N = 2 の場合を考える。question を次のようなパラメータで呼び出し、以下に示すような返答を得たとする。
| パラメータ | 戻り値 |
|---|---|
| question(2, 0, -1) | 2 |
| question(2, 1, -1) | 2 |
| question(1, 0, 1) | 1 |
| question(1, 1, 0) | 1 |
これは人 0, 1 の双方ともに正直者が 2 人いると主張し、また互いに互いを正直者であると主張していることを表す。
この質問の結果を満たすような組み合わせは人 0, 1 がともに正直者である場合とともに嘘つきである場合の 2 通りがあり、これ以上の質問は不可能である。したがって identify は impossible を呼び出して終了する必要がある。
小課題
小課題 1 (16 点)
- 1 ≦ N ≦ 10
- identify(N) は question(Q, i, j) を何度呼び出しても構わない。
小課題 2 (29 点)
- 1 ≦ N ≦ 1 000
- identify(N) は question(Q, i, j) を何度呼び出しても構わない。
小課題 3 (17 点)
- 1 ≦ N ≦ 100 000
- identify(N) が question(Q, i, j) を呼び出す回数は 200 500 回以下でなければならない。
小課題 4 (38 点)
- 1 ≦ N ≦ 100 000
- identify(N) が question(Q, i, j) を呼び出す回数は 100 500 回以下でなければならない。
実装の詳細
制限
- CPU 時間制限: 1 秒
- メモリ制限: 256 MB
注意: スタックのサイズには決められた制限はない。スタックとして使用されたメモリは、メモリ総使用量に含まれる。
インターフェース (API)
- 実装フォルダ: honest/ (プロトタイプ: honest.zip)
- 競技者が実装するファイル: または honest.cpp
- 提出ファイルのインターフェース: honest.h
- 採点プログラムのサンプル: または grader.cpp
- 採点プログラムの入力のサンプル: grader.in.1, grader.in.2, ...
注意:採点プログラムのサンプルは次の書式の入力を読み込む。- 1 行目: N
- 2 行目: N 個の整数 X[0], X[1], ..., X[N-1] が空白区切りで書かれている。X[i] は人 i が正直者か嘘つきかを表す。
- 3 行目: N 個の整数 A[0], A[1], ..., A[N-1] が空白区切りで書かれている。A[i] は人 i が正直者の人数を質問された際の返答を表す。
- 採点プログラムの入力のサンプルに対して期待される出力: grader.expect.1, grader.expect.2, ...
注意:採点プログラムのサンプルは次の書式の出力を書き出す。- 正直者が完全に特定可能な場合: N 個の整数 X[0], X[1], ..., X[N-1] が空白区切りで出力される。意味は入力のそれと同じである。
- 正直者を特定することが不可能な場合: 文字列 "Impossible." のみからなる1行が出力される。
- 採点プログラムのサンプルは標準エラー出力に次の書式で情報を書き出す。
- 1 行目: "#question = Q" が出力される。ただし Q はこの実行で question が呼び出された回数である。