Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
sは文字
m本の入力文字列s_1,...,s_mについて,それぞれの逆相補鎖配列を出力せよ.
制約
- s_1,...,s_mは
A ,C ,G ,T からなる文字列である. - 1 \leq m \leq 100とする.
- 1 \leq |s_1|, \ldots, |s_m| \leq 1000 (文字列xの長さを|x|と記述する.)
入力
入力は以下の形式で標準入力から与えられる.
m s1 s2 : sm
出力
入力文字列の逆相補鎖配列を出力せよ.各逆相補鎖配列は一行で出力し,対応する入力文字列と同じ順序で出力すること.
入力例 1
6 CATAGAACGACTATT TA GCGGCTTTTTGAAGCGT TACCTTGATCA GGCGTGCATAG T
出力例 1
AATAGTCGTTCTATG TA ACGCTTCAAAAAGCCGC TGATCAAGGTA CTATGCACGCC A
問題の背景
※ この項目は読まなくても問題を解くことができますが,出題の背景となりますため,ご興味を持ってくださった方はお読みいただけると幸いです.
DNAと塩基配列
生物の構成に必要な遺伝情報はDNAに保存されています.それでは,DNAはどのようにして遺伝情報を持つのでしょうか?
ヌクレオチドが鎖状に連なった物質を一本鎖DNAと呼びます.DNAは,長さが同じで対応関係のある二本の一本鎖DNAが結合してらせん構造を形成した物質です.ここではまず,一本鎖DNAについて説明をします. 一本鎖DNAを構成する各ヌクレオチドは塩基を一つ含みます.塩基はアデニン(adenin), シトシン(cytosin), グアニン(guanine),チミン(thymine) の4種類です.そのため,各ヌクレオチドの塩基を鎖の端から順に読み取ると,4種類の記号から成る配列と解釈することができます.鎖の両端は,ヌクレオチドの構造に応じて一方を5'末端,他方を3'末端と区別することができるため,一般的には,5'端から\rightarrow3'端の向きに記号を読み取って配列とみなします. この配列を,DNA配列,塩基配列,ゲノム配列などと呼びます.配列の各要素は塩基の頭文字により表現します.例えば下図のように,5'末端\rightarrow3'末端に向かってアデニン,シトシン,シトシン,チミンが並んでいる場合は,ACCTと表記します.
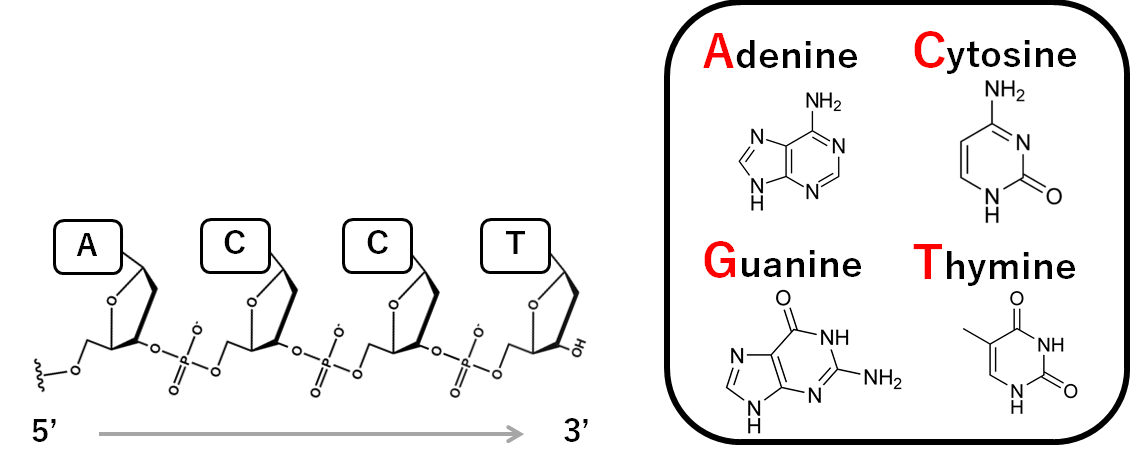
DNAの構造,逆相補鎖
一本鎖DNAの各塩基は,特定の別の塩基と結合する性質を持っています.具体的には,アデニン(A)はチミン(T)と,シトシン(C)はグアニン(G)と互いに結合します.DNAを構成する二本の鎖は,向かい合う塩基同士が全て結合するような塩基の並びをしており,それゆえに,二本の鎖が離れることなく二重らせんを形成できるのです.ここで注意が必要なのは,二本の鎖は互いに逆向きに並んでいるということです.下図の下の鎖では,5'末端\rightarrow3'末端に向かってアデニン(A),シトシン(C),チミン(T),グアニン(G)と並んでいます.上の鎖では5'末端\rightarrow3'末端に向かってシトシン(C),アデニン(A),グアニン(G),チミン(T)と並んでおり,それぞれの塩基は上の鎖の対応する塩基と結合しています.
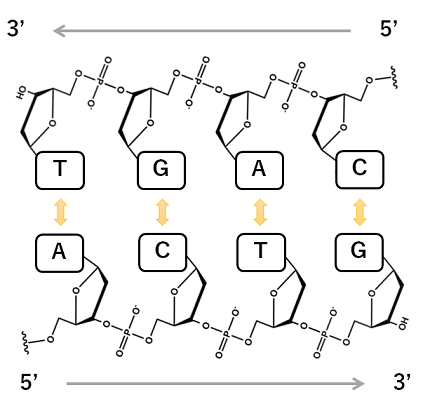
二重らせんを形成する一方の鎖に対して,もう一方の鎖を逆相補鎖と呼びます.図の例の場合,下の鎖の塩基配列はACTGと記述し,その逆相補鎖である上の鎖の塩基配列はCAGTと記述します.(TGACでないことに注意.) 二つの鎖は互いに対応関係のある塩基の並びをしているため,DNAは同一の情報を二重に保持しているといえます.そして,生物には一方の鎖に損傷が生じても,他方の鎖を元に損傷個所を復元する仕組みが備わっています. さて, DNAの遺伝情報は二本の鎖のどちらを読み出し元とするかによって,二通りの塩基配列で表記されることになります.例えば,DNAのある部分がAGGCと表記されている場合,その逆相補鎖の塩基配列であるGCCTと表記しても同じ情報とみなすことができるのです.
Score : 100 points
Problem Statement
s is a string consisting of characters
Output all the reverse complement sequences of m input sequences: s_1,...,s_m.
Constraints
- s_1,...,s_m are strings consisting of
A ,C ,G ,T . - 1 \leq m<100
- 1 \leq |s_1|, \ldots, |s_m| <1000 (the length of x is denoted by |x|.)
Input
Input is given from Standard Input in the following format:
m s1 s2 : sm
Output
Print reverse complement sequences of input sequences. Each sequence should be printed as a single line, and the order of the output sequences must be the same as the order of input sequences.
Sample Input 1
6 CATAGAACGACTATT TA GCGGCTTTTTGAAGCGT TACCTTGATCA GGCGTGCATAG T
Sample Output 1
AATAGTCGTTCTATG TA ACGCTTCAAAAAGCCGC TGATCAAGGTA CTATGCACGCC A
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
sとtは文字
S_{sop} = \sum_{i=1}^{N} sim(s[i], t[i])
ただし,Nは
| x \ y | |||||
| 1 | -3 | -3 | -3 | -5 | |
| -3 | 1 | -3 | -3 | -5 | |
| -3 | -3 | 1 | -3 | -5 | |
| -3 | -3 | -3 | 1 | -5 | |
| -5 | -5 | -5 | -5 | -5 |
例えば,s=
S_{sop} = sim(
のように計算することができ,S_{sop}が最大となる.
この時,
C-TCGGT CATCC--
このように,文字列中の適切な場所に空白
二本の入力文字列についてS_{sop}を最大化するペアワイズアラインメントを出力せよ.
制約
- sとtは
A ,C ,G ,T からなる文字列である. - 10 \leq |s|, |t| \leq 400 (文字列xの長さを|x|と記述する.)
入力
入力は以下の形式で標準入力から与えられる.
s t
出力
入力文字列のS_{sop}が最大となるペアワイズアラインメントを出力せよ.例に倣い,sとtの適切な位置に
入力例 1
AGTTGAATTT GTCGGACTTT
出力例 1
AGT-TGAATTT -GTCGGACTTT
問題の背景
※ この項目は読まなくても問題を解くことができますが,出題の背景となりますため,ご興味を持ってくださった方はお読みいただけると幸いです.
ペアワイズアラインメントはゲノム配列解析の様々な場面において用いられます.ここでは,個人のゲノム配列解析について考えてみたいと思います.
DNAからゲノム配列を読み出す装置をシークエンサーと呼びます.ヒトのゲノム配列は全長30億塩基に及ぶ非常に長い配列ですが,シークエンサーはこの長い配列を端から端まで一気に読み出せるわけではありません.装置によって読み出しの長さは異なりますが,短いもので数百,長いもので数百万塩基程度の断片を読み出すのです.ですから,読み取った断片配列がゲノム上のどの部分に相当するのか突き止めなければなりません.そこで,既に決定されているヒトの標準的なゲノム配列(参照ゲノム配列と呼ぶ)と見比べて,読み取った断片配列の位置を特定するのです.ここで注意しなければならないのは,読み出した断片配列とそれに対応する参照ゲノムの部分配列には違いがあるという点です.差異が生じる理由は二つあります.一つは,ゲノム配列は個人(個体)ごとに少しずつ異なるためで,もう一つはシークエンサーがゲノム配列を読み出す際にエラーを発生させてしまうためです.これら二つに共通するのは,参照ゲノム配列に対して次のような差異が比較的多く生じるということです.
置換(ある文字が別の文字に置き換わっている.)
ATGC ← 参照ゲノム配列 ATCC ← 読み出した個人のゲノム配列
欠損(ある文字が欠損している.)
ATGC ← 参照ゲノム配列 AT-C ← 読み出した個人のゲノム配列
挿入(ある文字が追加されている.)
ATC-C ← 参照ゲノム配列 ATCAC ← 読み出した個人のゲノム配列
このような差異のある配列同士の類似部分をうまく並べるために,ペアワイズアラインメントが必要となるのです.
なお,ゲノム配列全長とシークエンサーで読み出した断片配列のように長さが大きく違う配列をアラインメントするには様々な工夫が必要となります.また,良いアラインメントを作るためには類似度の設計も重要です.例えば,挿入があまり入らないと予想されるケースでは
シークエンサーについて
さて,上の文章で書いた「個人のゲノム配列解析」が気軽にできるようになったのは,実はごく最近のことなのです.次のグラフをご覧ください.(NIHより引用)
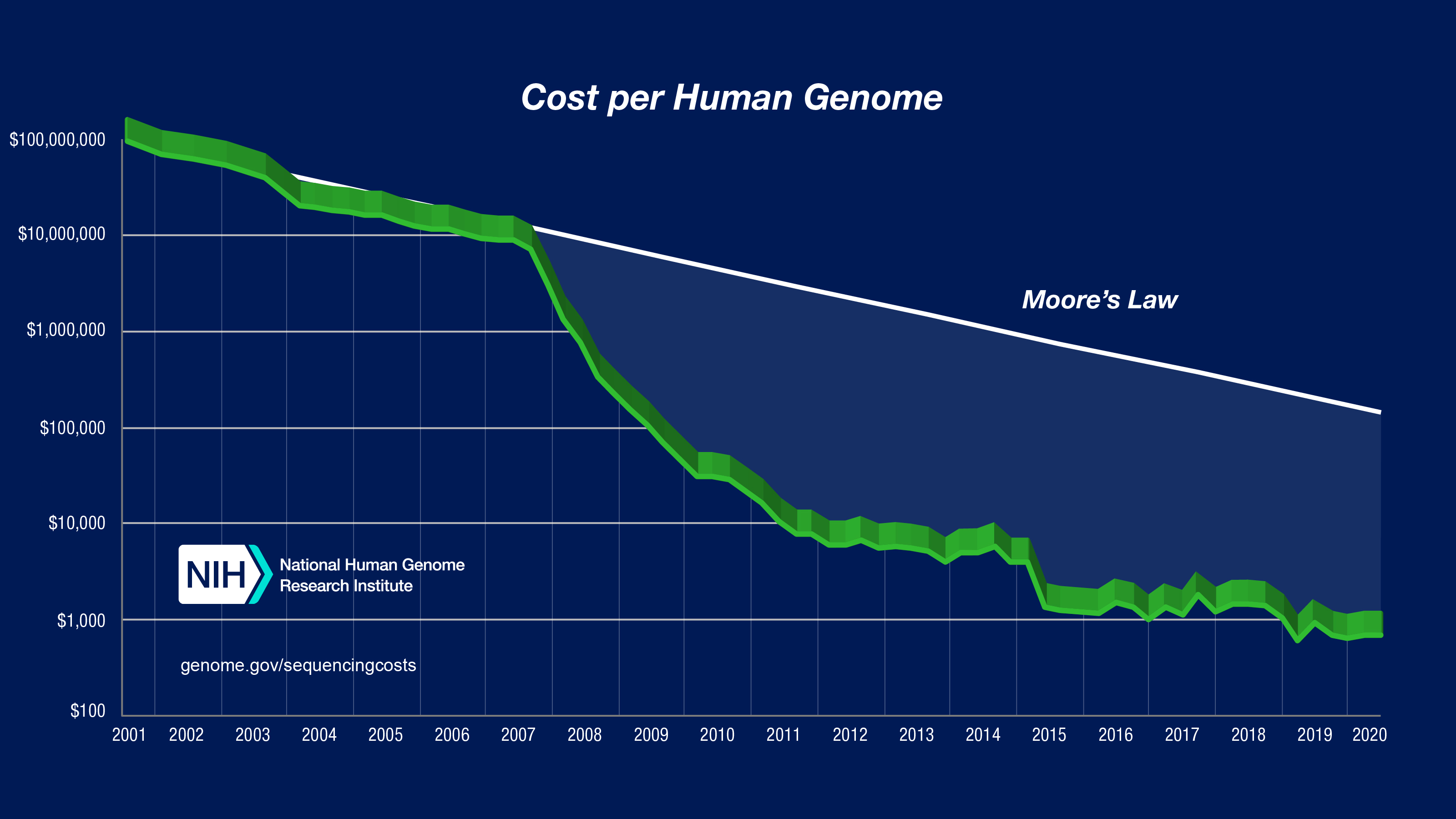
こちらは,アメリカ国立衛生研究所(National Institute of Health)が試算した一人分のヒトゲノムを読みとるのに必要な金額を示したグラフです.縦軸がコスト,横軸が年を示しています.現在の読み取り費用は約10万円ですが,20年前はなんと100億円必要だったのです.グラフを見ると,2000年代後半から急激にコストが下落しているのがわかると思います.一体,何が起きたのでしょうか?
実は,上述の「シークエンサー」に技術革新が起き,読み取り(シークエンシングと呼びます)コストが劇的に下がったのです.シークエンサーの性能向上は,生命科学の研究を大きく前進させました.そして同時に,同分野における計算機科学の重要性も大きく高めることになったのです.考えてみてください,個人の設計図が10万円で手に入るのです.世界中の研究機関では膨大なデータが算出されます.各設計図は30億塩基対に及ぶ大きさで,シークエンサーは設計図の断片を(多少のエラーを含めながら)大量,かつバラバラに読み出してくるのです.優れたアルゴリズムなくして解析を遂行することはできません.
シークエンサーの性能向上は日進月歩のため,その出力データを解析するアルゴリズムにも日進月歩の向上が求められています.D問題で使うデータは,Oxford Nanopore Technologies社のシークエンサーによるものです.こちらは,読み取り長がとても長いという優れた特徴を持ち,多くの解析の現場で用いられています.今回は,最新のキットQ20を用いて読み出したデータとなることにもご注目ください.
Score : 500 points
Problem Statement
s and t are strings consisting of
S_{sop} = \sum_{i=1}^{N} sim(s[i], t[i])
sim(x,y) is a function for calculating the similarity of x and y, and the following table defines its output.
| x \ y | |||||
| 1 | -3 | -3 | -3 | -5 | |
| -3 | 1 | -3 | -3 | -5 | |
| -3 | -3 | 1 | -3 | -5 | |
| -3 | -3 | -3 | 1 | -5 | |
| -5 | -5 | -5 | -5 | -5 |
For example when s=
S_{sop} = sim(
Note that s and t with balnk symbols are aligned such that same character appears at same position in each string for many positions.
C-TCGGT CATCC--
We call this task pairwise alignment and described it as strings in two lines.
Given two strings, output its pairwise alignment such that it maximizes S_{sop}.
Constraints
- s and t are strings consisting of
A ,C ,G ,T . - 10 \leq |s|, |t| \leq 400 (length of a string x is denoted by |x|.)
Input
Input is given from Standard Input in the following format:
s t
Output
Print a pairwise alignment of input strings such that S_{sop} is maximized.
After inserting
s should be printed in the first line, and t should be printed in the second line. If there is more than one alignment that maximizes S_{sop}, you can print any one of them.
The judging system can only accept user's output when:
- The first line/second line is equal to the first line/second line of the input if
Sample Input 1
AGTTGAATTT GTCGGACTTT
Sample Output 1
AGT-TGAATTT -GTCGGACTTT
Time Limit: 10 sec / Memory Limit: 1024 MiB
問題文
文字
C(t) = min_{x \in \{A, T, G, C, -\}} \left| \{ t[i] \; | \; t[i] \neq x \; (i=1, \ldots, m) \} \right|
平たく言うと,C(t)はtに含まれる文字の中で最も出現回数の多い文字以外の文字の数となる.例えば,t=
Sのすべての列ベクトルについてC(S_{*,j})を計算し,その総和が少ないほど,同じ列に同じ文字が多く出現するように入力文字列をそろえることができていると言えるであろう.このように,文字列中の適切な場所に空白
例えば,3本の文字列
GGATC GGAT- G-ACC
C_{all}(S) = C(S_{*,1}) + C(S_{*,2})+ C(S_{*,3})+ C(S_{*,4})+ C(S_{*,5}) = 0 + 1 + 0 + 1 + 1 = 3 となる.
m本の文字列 s_{1}, \ldots, s_{m} が与えられたとき,C_{all}(S)をできるだけ小さくするマルチプルアラインメントを出力せよ.
制約
- s_1,...,s_mは
A ,C ,G ,T からなる文字列である. - テストケース(small)の場合
- 8 \leq m \leq 10とする.
- 80 \leq |s_1|, \ldots, |s_m| \leq 100 (文字列xの長さを|x|と記述する.)
- テストケース(large)の場合
- 35 \leq m \leq 40とする.
- 700 \leq |s_1|, \ldots, |s_m| \leq 750
入力
入力は以下の形式で標準入力から与えられる.
m
s_{1}
s_{2}
:
s_{m}
出力
入力文字列についてC_{all}をできるだけ小さくするマルチプルアラインメントを出力せよ.例に倣い,各文字列の適切な位置に
入力例 1
10 GGAGGTTATTGCTGTGGAGGTACTGGAGAAGGAGGATGCTAGCGTTGGGTAAACCACGAGCATTTTGACTTGTACTTCGCCTC GGGTTATTGCTGTTGTGAGTACTGGAGACAGGAGGGAGTGTTAGAGTTGGGGTAAACCACAGTAGCTCATGTCACTTGGATAACTCGTCAGCCTC GGTCACTCGCTGTGGAGAGTACTTTGAGACAGGAGGGAGTGCTAGAGTTTGGGGTAAAACCACAGCAGCTCATGCACTTGGATATCTGTGAGCC GAGGTTAGTGCTGTGGAGAGTACTGGAGACAGGAGGGAGTGCTAGAGTTGGGGTAAAGCACAGCACCATTCACTGATAAATGTCAGGCCTAGGGG GAGGTATTGCTGTGGAGGGTACTGGAGACAGGAGGAGTGCTAGAGGTTGGGGTAAAACCACAGCAGCTCATTTACTTGATACTGTCAGGCTCAGG GAGGTTATTTGCTGTGGAGAGTTACTGAGACATGGGGTGCCAAGTTGGGTAGCTACAGCAGCTCATTTCACTTGATACTGCAGGCTCTCAG GAGTTAATTTCGTGGAGAGTACTAGAGCACAGGAGGGAGGCCAGATTGGGGTATACCACAGCAGCTCGTTCACTTTAACTGTCAGGCCCTCA ACAGTTTAATTGATGGGCGGAGAGTACTGGAGACAGGAGGGAGTGCTAGAGTGGGGTAAACCACAGCAGCATCTTTCATTATAACTGTCAG CAAGGTTTTTTCGCTGTGGAGAGTACTGGAGACCGGGGAGTGTAGACTTTGGGGTATCACGTAGCAGCTTATTTCGACTTTGTACTGTAA GAGTTATTTCTGTGGAGAGAACTGGAGACGGAGGGAGTGCTAGAGTTGGGGTAAACACCAGGCAGCCATTTCACTTGATAACTGTCAGGCCTT
出力例 1
GGAGGTTA-TTGCT--GTGGAG-GTAC-TGGAGA-AGGA-GGA-TGCTAGCG-TT-GGGT-AAACCAC-G-AGC-ATTTTGACTT-G-T-ACT--TC-GCCTC---- --GGGTTA-TTGCT--GTTGTGAGTAC-TGGAGACAGGAGGGAGTGTTAGAG-TTGGGGT-AAACCACAGTAGCTCATGTCACTTGGATAACTCGTCAGCCTC---- ---GGTCACTCGCT--GTGGAGAGTACTTTGAGACAGGAGGGAGTGCTAGAGTTTGGGGTAAAACCACAGCAGCTCATG-CACTTGGATATCT-GTGAG-C-C---- -GAGGTTA-GTGCT--GTGGAGAGTAC-TGGAGACAGGAGGGAGTGCTAGAG-TTGGGGT-AAAGCACAGCA-CCATTCACTGATAAATGTCAGGCCTAGGGG---- --GAGGTA-TTGCT--GTGGAGGGTAC-TGGAGACAGGA-GGAGTGCTAGAGGTTGGGGTAAAACCACAGCAGCTCAT-TTACTT-GAT-ACT-GTCAGGCTC-AGG -GAGGTTATTTGCT--GTGGAGAGTTACT-GAGACA--TGGG-GTGCCA-AG-TT-GGGT--AGCTACAGCAGCTCATTTCACTT-GAT-ACT-G-CAGGCTCTCAG --GAGTTAATTTC---GTGGAGAGTACTAGAGCACAGGAGGGAG-GCCAGA--TTGGGGT-ATACCACAGCAGCTCGT-TCACTT---TAACT-GTCAGGC-CCTCA ACAGTTTAATTGATGGGCGGAGAGTAC-TGGAGACAGGAGGGAGTGCTAGAG--TGGGGT-AAACCACAGCAGCATCTTTCA-TT--ATAACT-GTCAG-------- CAAGGTT-TTTTCGCTGTGGAGAGTAC-TGGAGAC-CG-GGGAGTG-TAGACTTTGGGGT---ATCAC-GTAG--CAGCTTATTTCG--ACTTTGT-A--CT-GTAA --GAGTTA-TTTCT--GTGGAGAGAAC-TGGAGAC-GGAGGGAGTGCTAGAG-TTGGGGT-AAACACCAGGCAGCCATTTCACTT-GATAACT-GTCAGGC-C--TT
配点
提出プログラムは「制約」の項目に記載した2種類のテストケース(smallとlarge)により評価される.smallに該当するケースは2つ,largeに該当するケースは8つ用意されている.制限時間内に正しい記述で出力された結果のみが評価の対象となる. smallの場合は各テストケースにつき,\{200 - \lfloor C_{all}(S) * 0.2 \rfloor \}または0のいずれか大きい方の値が得点に加算される.largeの場合は,\{700 - \lfloor C_{all}(S) * 0.1 \rfloor \}または0のいずれか大きい方の値が得点に加算される.例えば,制限時間内にsmallのケースのみ2つ回答できた場合は, max\{200 - \lfloor C_{all}(S_1) * 0.2 \rfloor, 0\} + max\{200 - \lfloor C_{all}(S_2) * 0.2 \rfloor, 0\}が得点となる.(ただし,S_1, S_2はそれぞれのケースの出力.)
なお,最良の解が最大点(4500 6000点)に到達できることは保証しない.また,最終的な順位はコンテスト終了後に別のデータセットで評価する.現在ジャッジシステムに設置されているデータとコンテスト終了後に使用するデータセットは同じ方法で生成する.
データ生成方法
参照ゲノム配列の一部(ヒトの22番染色体)から部分文字列sを切り出す.ただし,
問題の背景
※ この項目は読まなくても問題を解くことができますが,出題の背景となりますため,ご興味を持ってくださった方はお読みいただけると幸いです.
マルチプルアラインメントは,ペアワイズアラインメントと同様に,ゲノム配列解析の様々な場面において用いられます.ここでは,まず,ウィルスの変異解析について考えてみたいと思います.
ウィルスに感染すると,生体内ではウィルスのコピーがたくさん作られるのですが,その際,設計図となるDNAもしくはRNAも複製されます.しかし,複製の精度は100%ではないため,複製のたびに,新たに作られるウィルスのゲノムには様々な変異(置換,挿入,欠損など)が生じます.そのため,ゲノム配列が少しずつ異なるウィルスがたくさんできてしまうのです.このように少しずつ異なるけれど,大凡は似ている配列を比較して,変異の特徴を分析するのにマルチプルアライメントは役立ちます.
そのほかにも,シークエンサーから読み出された断片配列のエラー訂正にも使われます.DNAからゲノム配列を読み出す際には,シークエンサーのエラーを後で修正できるように,ゲノム上の同じ箇所を重複して読み取ります.こうして得られた断片配列には,読み出した際の状況に応じてエラーが含まれますが,これらの断片配列についてマルチプルアラインメントを作成して,各列について多数決をとれば,エラーを訂正することができます.
Problem statement
Given m strings consisting of
C(t) = min_{x \in \{A, T, G, C, -\}} \left| \{ t[i] \; | \; t[i] \neq x \; (i=1, \ldots, m) \} \right|
C(t) counts the number of characters in t that are not equal to the one that appears in t the most frequently. For example, when t=
If we can generate S such that sum of C(S_{*,j}) for all columns becomes small, it is expected that the given m strings are well aligned. We call such a problem multiple alignment and define the following score.
C_{all}(S) = \sum_{j=1}^n C(S_{*,j})
For example, if we align the three strings
GGATC GGAT- G-ACC
The score C_{all}(S) becomes C(S_{*,1}) + C(S_{*,2})+ C(S_{*,3})+ C(S_{*,4})+ C(S_{*,5}) = 0 + 1 + 0 + 1 + 1 = 3.
Given m strings s_{1}, \ldots, s_{m}, output a multiple alignment such that C_{all}(S) becomes small as much as possible.
Constraints
- s_1,...,s_m are strings consisting of
A ,C ,G ,T . - Test case (small)
- 8 \leq m \leq 10.
- 80 \leq |s_1|, \ldots, |s_m| \leq 100 (the length of x is denoted by|x|.)
- Test case (large)
- $35 \leq m \leq
- 700 \leq |s_1|, \ldots, |s_m| \leq 750
Input
Input is given from Standard Input in the following format:
m
s_{1}
s_{2}
:
s_{m}
Output
Print a multiple alignment of input strings such that C_{all} becomes small as much as possible.
After inserting
The judging system can only accept user's output when:
- Each line is equal to the corresponding input line if
Sample Input 1
10 GGAGGTTATTGCTGTGGAGGTACTGGAGAAGGAGGATGCTAGCGTTGGGTAAACCACGAGCATTTTGACTTGTACTTCGCCTC GGGTTATTGCTGTTGTGAGTACTGGAGACAGGAGGGAGTGTTAGAGTTGGGGTAAACCACAGTAGCTCATGTCACTTGGATAACTCGTCAGCCTC GGTCACTCGCTGTGGAGAGTACTTTGAGACAGGAGGGAGTGCTAGAGTTTGGGGTAAAACCACAGCAGCTCATGCACTTGGATATCTGTGAGCC GAGGTTAGTGCTGTGGAGAGTACTGGAGACAGGAGGGAGTGCTAGAGTTGGGGTAAAGCACAGCACCATTCACTGATAAATGTCAGGCCTAGGGG GAGGTATTGCTGTGGAGGGTACTGGAGACAGGAGGAGTGCTAGAGGTTGGGGTAAAACCACAGCAGCTCATTTACTTGATACTGTCAGGCTCAGG GAGGTTATTTGCTGTGGAGAGTTACTGAGACATGGGGTGCCAAGTTGGGTAGCTACAGCAGCTCATTTCACTTGATACTGCAGGCTCTCAG GAGTTAATTTCGTGGAGAGTACTAGAGCACAGGAGGGAGGCCAGATTGGGGTATACCACAGCAGCTCGTTCACTTTAACTGTCAGGCCCTCA ACAGTTTAATTGATGGGCGGAGAGTACTGGAGACAGGAGGGAGTGCTAGAGTGGGGTAAACCACAGCAGCATCTTTCATTATAACTGTCAG CAAGGTTTTTTCGCTGTGGAGAGTACTGGAGACCGGGGAGTGTAGACTTTGGGGTATCACGTAGCAGCTTATTTCGACTTTGTACTGTAA GAGTTATTTCTGTGGAGAGAACTGGAGACGGAGGGAGTGCTAGAGTTGGGGTAAACACCAGGCAGCCATTTCACTTGATAACTGTCAGGCCTT
Sample Output 1
GGAGGTTA-TTGCT--GTGGAG-GTAC-TGGAGA-AGGA-GGA-TGCTAGCG-TT-GGGT-AAACCAC-G-AGC-ATTTTGACTT-G-T-ACT--TC-GCCTC---- --GGGTTA-TTGCT--GTTGTGAGTAC-TGGAGACAGGAGGGAGTGTTAGAG-TTGGGGT-AAACCACAGTAGCTCATGTCACTTGGATAACTCGTCAGCCTC---- ---GGTCACTCGCT--GTGGAGAGTACTTTGAGACAGGAGGGAGTGCTAGAGTTTGGGGTAAAACCACAGCAGCTCATG-CACTTGGATATCT-GTGAG-C-C---- -GAGGTTA-GTGCT--GTGGAGAGTAC-TGGAGACAGGAGGGAGTGCTAGAG-TTGGGGT-AAAGCACAGCA-CCATTCACTGATAAATGTCAGGCCTAGGGG---- --GAGGTA-TTGCT--GTGGAGGGTAC-TGGAGACAGGA-GGAGTGCTAGAGGTTGGGGTAAAACCACAGCAGCTCAT-TTACTT-GAT-ACT-GTCAGGCTC-AGG -GAGGTTATTTGCT--GTGGAGAGTTACT-GAGACA--TGGG-GTGCCA-AG-TT-GGGT--AGCTACAGCAGCTCATTTCACTT-GAT-ACT-G-CAGGCTCTCAG --GAGTTAATTTC---GTGGAGAGTACTAGAGCACAGGAGGGAG-GCCAGA--TTGGGGT-ATACCACAGCAGCTCGT-TCACTT---TAACT-GTCAGGC-CCTCA ACAGTTTAATTGATGGGCGGAGAGTAC-TGGAGACAGGAGGGAGTGCTAGAG--TGGGGT-AAACCACAGCAGCATCTTTCA-TT--ATAACT-GTCAG-------- CAAGGTT-TTTTCGCTGTGGAGAGTAC-TGGAGAC-CG-GGGAGTG-TAGACTTTGGGGT---ATCAC-GTAG--CAGCTTATTTCG--ACTTTGT-A--CT-GTAA --GAGTTA-TTTCT--GTGGAGAGAAC-TGGAGAC-GGAGGGAGTGCTAGAG-TTGGGGT-AAACACCAGGCAGCCATTTCACTT-GATAACT-GTCAGGC-C--TT
Points
The submitted program is evaluated by two test case types: Small and Large, as denoted in the Constraints section. Small contains two cases, and Large contains eight cases. The points are given to outputs that satisfy the format within the time limit. For each output of a test case in Small, a contestant earns \{200 - \lfloor C_{all}(S) * 0.2 \rfloor \} or 0, whichever is greater. For a test case in Large, the contestant earns \{700 - \lfloor C_{all}(S) * 0.1 \rfloor \} or 0, whichever is greater. For example, if one can generate two outputs S_1 and S_2 for Small-type cases with a correct format within the time limit, one can earn max\{200 - \lfloor C_{all}(S_1) * 0.2 \rfloor, 0\} + max\{200 - \lfloor C_{all}(S_2) * 0.2 \rfloor, 0\}.
We do not guarantee that the optimal solution can achieve the maximum points (6000 points). The final standings are determined by the other dataset generated by the same method used to generate the current test cases.
The method for generating test cases
We extract substring s from chromosome 22 of the human reference genome sequence in the first step. s is extracted such that it does not include
Time Limit: 2 sec / Memory Limit: 2048 MiB
更新履歴
- 28th September, 2021 (JST): コンテスト終了に伴い,テストケースを削除しました.また,サンプルデータの配布も終了しました.D問題は,問題文のみの公開となります.プログラムを提出してもジャッジは行われません.コンテスト開催時の実行時間制限は30秒でした.
- 11th September, 2021 (JST): サンプルデータのダウンロードに必要な情報を追記しました.
- 10th September, 2021 (JST): Sample2 終端記号が抜けているのを直しました. 本文中の f = 0 という誤りを f = > に修正しました.ダウンロードできるサンプルデータに
- やX が含まれる理由の解説を加えました. - 9th September, 2021 (JST): ダウンロードデータセットに関する注意書きを追加しました.
- 9th September, 2021 (JST): 日本語の問題文を公開しました.ジャッジサーバーが動いています.
追加情報(トップページより転載)
- 2021/9/12 : D問題に関しまして,Dockerによる手元ジャッジ環境を準備しました.こちら(GitHub)よりダウンロードできます.手元でのジャッジの他,入力のパース,非常に基本的な解を出力するプログラムも含まれております.
- 2021/9/12 : D問題に関しまして,BAM形式のビューア―の使い方を記載した資料を準備しました.こちらからダウンロード頂けます.
ストーリー
あなたは Oxford Nanopore Technologies 社の最新機器である PromethION を手に入れた!PromethION は DNA を読み取る機械である.この機械を用いてあなたは自分の DNA 配列を解析しようと試みた.しかし,PromethION はあなたの DNA 配列を端から端まで100%正確に読み取れるわけではない.PromethION に投入するために DNA を精製すると,DNA は千切れてバラバラになってしまう.このため,1回の観測で得られる配列はDNA 配列の一部分だけだ.また,観測エラーもあるため,読み取ったDNA配列の断片配列の集合からあなたのDNA配列を精密に予測することは簡単ではない.あなたのミッションは,PromethION の出力データからあなたの真の DNA 配列を推測することである.あなたの DNA 配列には父から受け継いだ配列と母から受け継いだ配列の2本があり,2本ともなるべく正確に推測したい.
問題文
文字
(1) 観測は以下の「観測試行」をn 回繰り返すことで行われ, n 本の文字列を得る.
(2) 観測試行で得られた n 本の文字列に対して以下の操作を行う.
(2a) s_1, s_2 と似ている(と出題者が考えている)配列 r が存在する. この配列 r と観測試行で得られた n 本の文字列をそれぞれペアワイズアラインメント(ペアワイズアラインメントの定義は問題Bを参照)する
(2b) ペアワイズアラインメントの結果(n 個)と r を合わせて結果 B とする.結果 B に含まれる n 個のペアワイズアラインメントは全て配列 r と同じ向きに揃えられている.
観測試行
(1) s_1 と s_2 のどちらかをそれぞれ 50% の確率で選択し,選択した文字列を s_i とする.
(2) 選択した文字列s_iに対して始点の座標b を一様ランダム (-l_i \le b \le l_i) に, 終点の座標 e を e - b がある分布に従うように決める. e が 0 以下となった場合には観測試行を (1) からやり直す.
(3) b が 1 以下である場合には b に 1 を代入する. e が l_i より大きい場合には e に l_i を代入する.
(4) t = s_i [b: e] (s_i の b 文字目から e 文字目)と置く.
(5) 50% の確率で t に t の逆相補鎖(逆相補鎖問題の定義はA参照)を代入する. 代入したときには f =
(6) t を観測してf と文字列を出力する. 文字列観測の際にはエラーが発生する. エラーの種類には, 文字が別の文字に置き換わってしまう置換, 文字が増減する挿入や欠失がある. 詳しくは観測エラーについての補足を参照のこと.
くだけた問題の説明

実際の観測試行では始点の座標と終点の座標がバラバラであり,n 本の観測試行を重ねて表示したものを縮小して表示した一例を以下に示す.A, C, G, T がそれぞれ異なる色に割り当てられており,スペース節約のために観測試行はなるべく上に詰めて表示している.また,各観測試行の端にグレーの三角印が付いているが観測試行の向き f を表している.大きな欠失は細い水平の黒線で表されており,挿入は潰れて認識しにくく表示されている.

観測エラーについての補足
観測エラーは置換,挿入,欠失の3種類からなる.観測エラーはシミュレーションではなく実機の PromethION と開発中の試薬を用いることで結果として含まれているため,どのような時にどれぐらいの頻度でどのようなエラーが入るかは出題者にも厳密には分からない.観測エラーの性質を分析できるように,既知の DNA 配列を PromethION で読んだデータが別途ダウンロード可能である(後述).
置換
ある文字が別の文字に置き換わる.以下の例では2文字目の
元文字列 : ACCAG 観測文字列: AGCAG
挿入
元文字列には存在しない配列(任意長)が観測文字列に追加される.以下の例では元文字列の2文字目と3文字目の間に
元文字列 : ACGAG 観測文字列: ACAAGAG
欠失
元文字列に存在する配列(任意長)が観測文字列に現れない.以下の例では元文字列の3文字目に存在する
元文字列 : ACGAG 観測文字列: ACAG
制約
- s_1, s_2は
A ,C ,G ,T からなる文字列である. - 3 \leq l_1, l_2 \leq 101,000とする.
- n \le 200 である
入力
入力は以下の形式で標準入力から与えられる.
g
f_{1} r_{1} c_{1}
f_{2} r_{2} c_{2}
:
f_{n} r_{n} c_{n}
=
観測した DNA の断片配列が n 本与えられるが,入力データサイズを節約するために n 本の配列は圧縮表記で与えられ,標準的な DNA 配列とそこからの差分という形式で与えられる.入力1行目の g は標準的な DNA 配列であり,1 文字以上 101,000 文字以下の文字列である.
続いて入力の 2 行目以降を説明する.2 行目からn+1 行目では 1 行につき 1 本の観測したDNA断片配列が記述される.各行最初の f_i は参照配列に対する DNA の向きを与える.DNA の向きは右向き(g と同じ向き)の場合には
「タイプ」には参照ゲノム配列との一致を表す
入力の終端は
「タイプ」について詳細を説明するため,一致,不一致,欠失,挿入それぞれについて,以下で具体例を示す.
一致の例
観測試行回数 n=1 の例を使って一致を説明する.以下に示すのは1 本の配列だけを入力とする入力例とそれに対応する1本の観測配列である.
ACGTGCTTA > 0 6= =
ACGTGC
もう1つの入力例とそれに対応する1本の観測配列を示す.
ACGTGCTTA < 2 4= =
GTGC
この例は初期カーソル位置を変えた例となっている.先頭から 2 文字スキップした位置がカーソル位置であり,そこから 4 文字を出力し
以下の入力例では
ACGTGCTTA < 1 2=3= =
CGTGC
不一致の例
標準ゲノムとは異なる文字を出力する場合にはタイプ
ACGTGCTTA > 0 3=2XGA4= =
ACGGACTTA
対応関係を見やすく書くと,以下のようになる.標準ゲノムを g とし,観測配列を A として示した.見やすさ一のために,一致する文字の間に
g: ACGTGCTTA |||XX|||| A: ACGGACTTA
欠失の例
標準ゲノムに対して欠失がある場合にはタイプ
ACGTGCTTA < 1 2=1D4= =
CGGCTT
この観測配列 A と標準ゲノム g の対応関係を見やすく書くと以下のようになる.一致する文字が縦に並ぶ方が見やすいため観測配列 A に
g: ACGTGCTTA
|| ||||
A: CG-GCTT
挿入の例
標準ゲノムに対して挿入がある場合にはタイプ
ACGTGCTTAG > 2 2=2IAT3= =
GTATGCT
同様に標準ゲノム g と観測配列 A の対応関係を見やすく書くと以下のようになる.一致する文字が縦に並ぶ方が見やすいため g に
g: ACGT--GCTTAG
|| |||
A: GTATGCT
圧縮表記に関する補足
標準的なDNA配列とn 本の観測文字列の間の対応関係は,ゲノム業界で標準的なツールの1つを使って計算されているため,多くの場合には配列間の関係は正しいと考えられる.しかし,対応関係が間違っている場所もあることに注意されたい.例えば以下の例において,標準ゲノム g と観測対象のゲノム T の間の真の対応関係(神が存在してDNAシークエンサーの観測エラーがどのように発生したかが分かり,真に対応する文字を上下に並べた場合)が以下のようになっていた場合であっても, 観測配列A のような誤った対応関係が出力されていることがある.
g: ACGTGCGTAGCG ||| | |||| T: ACG--C--AGCG ||| |||| A: ACGC----AGCG
このような並べ間違いは入力中に多く含まれているがこのような間違いを修正することでスコアを向上させることができる可能性がある.
また,圧縮表記の取り扱いはコンテストの主眼ではないため,参加者にとってデバッグが容易になるように Python で圧縮表記からマルチプルアラインメント(マルチプルアラインメントについては問題Cを参照のこと)を生成する Python 3 向けのサンプルコード を用意した.第一引数に本問題の入力データ例のファイルを与えるとテキスト表記のマルチプルアラインメントを出力する.
出力
推測した2本の秘密配列を2行に分け,1行に1配列ずつ出力する.出力する配列には
スコア
出力された2本の配列を o_1, o_2 とする. もし o_1, o_2 を入れ替えた場合にスコアが上がる場合には入れ替えたうえでスコアを計算する.
o_1 と s_1, o_2 と s_2 を比較し, 1 文字正解するごとに 0.01 点が与えられる. 1 文字不正解(1文字の置換・1文字の欠失・1文字の挿入)するごとに 0.99 点を失う.
ただし,ある座標において モザイク化することでスコアが上がる場合にはモザイク化を行ってスコアを計算する.モザイク化とは,2本の秘密配列を推定する際に途中で配列が入れ替わる推定ミスをしてしまった場合にそれを救済する操作である. モザイク化の例を以下に示す.復元した秘密文字列が以下の例では途中の1箇所(空白を入れて強調した.この空白の座標をモザイク座標と呼ぶ)で入れ替わってしまっているが,モザイク化を行うとモザイク座標前後で o_1, o_2 の配列を入れ替えることができ,以下の例ではモザイク化を行うことで o_1, o_2 に含まれている全ての文字が s_1, s_2 に一致している.ただし,モザイク化は最大で 1 回しか行うことができず,モザイク化を行うとペナルティとして7.5点を失う.
モザイク化の例
s_1: GTC ACCGTGCAG s_2: AACG ACGGACATG o_1: AACG ACCGTGCAG o_2: GTC ACGGACATG
スコアに関する留意点1
本問題の入力データは完全に実データを用いて行っている.つまり,実際のヒトDNA配列をDNAシークエンサーに投入し,出力データの一部を切り取って用いている.また,正解となる2本の配列も実際のヒトDNA配列を DNAシークエンサーを含む様々な機器によって観測した桁違いに膨大なデータから業界でベストに近い知恵を集めて作成している.これは何を意味するかと言うと,入力データから満点となる2本の配列が出力できることは全く保証されていない.また,正解データとしてジャッジが用いているデータは極めて精度が高いと考えられるものの,100%正しいとは限らない.問題文に記述されていない偏りなども多く存在していると考えられる.判断に迷ったら,常にデータを信じて欲しい.
スコアに関する留意点2
本問題では現実世界でより役に立つ解答をより髙い点数で評価したいと考えている.このため,現状でサーバーにアップロードされているデータセットのみに対して過学習したアルゴリズムの解答を低い点数で評価したい.例えば乱数シードを用いたアルゴリズムを作り,異なるシードの解答を多数アップロードして最も高い点数をたたき出した乱数シードを最終版とする,といった現実世界で役に立たない解答の点数を低くしたい.このため,プログラム提出が締め切られた後でジャッジデータを追加して最終採点とする.合計点の理論値最大は3万点を目指しているが,実データを元にしているため 10% 前後の誤差があることを予め承知されたい.
サンプル1
2種類の短い秘密文字列があるパターンである.
入力例 1
ACACAGCGGCGACC > 0 3=1XT10= < 0 14= < 0 9=1D4= < 0 14= < 0 14= < 0 9=1D4= =
出力例 1
ACACAGCGGCGACCT ACATAGCGGGACT
入力をマルチプルアラインメント形式に見やすく表示したもの
Gは参照配列を表す.
G : ACACAGCGGCGACC 0 >: ACATAGCGGCGACC 1 <: ACACAGCGGCGACC 2 <: ACACAGCGG-GACC 3 <: ACACAGCGGCGACC 4 <: ACACAGCGGCGACC 5 <: ACACAGCGG-GACC
サンプル2
2種類の短い秘密文字列が完全に同一,もしくは違いがあっても入力からは違いを断定できないパターンである.
入力例 2
ACCGGTTGGCGTG > 0 5= < 1 8= > 2 2=1XA3=1IC3= < 4 5=1D2= > 7 6= =
出力例 2
ACCGGTTGGCGTG ACCGGTTGGCGTG
入力をマルチプルアラインメント形式に見やすく表示したもの
R : ACCGGTTG-GCGTG 0 >: ACCGG 1 <: CCGGTTG-G 2 >: CGATTGCGCG 3 <: GTTG-G-GT 4 >: G-GCGTG
もう少し大きなサンプル
ジャッジサーバの計算資源には限りがあり,提出は最大で2時間に1回に制限されている.参加者の皆様の手元の計算機上でデータを検討できるように,より実用的なサンプルデータをいくつかダウンロードできるように準備した.以下のデータはサンプルデータをゲノム業界の標準形式の一つである BAM ファイルに変換し,世界的に良く使われているビューワーの一つである IGV で閲覧できる.IGV の利用方法については今後追記される.また,入力データと解答データを元に皆様の手元の計算機上で採点できるように採点プログラムを用意した.このプログラムを用いて手元の計算機で採点する場合には一切の制限がないため,デバッグや開発に役立てて欲しい.
以下の Answer Data には2行で秘密配列 s_1, s_2 に相当する配列が格納されている。但し、ジャッジが採点する際にスコアを高速に計算できるように s_1 と s_2 の正解ペアワイズアラインメントを作成し
※本データセットは本コンテストに供するために Oxford Nanopore Technologies 社から提供されたデータを含んでいます.ここでダウンロードしたデータをコンテスト以外の目的に利用することはできません.また,コンテスト終了後にはデータは消去してください. 採点プログラム(gen1_small_10.testcase.txtを含む)と以下のデータのダウンロードには,IDとパスワードの入力が必要です.IDは「genocon2021」パスワードは「ontQ20」となります.IDとパスワードは他所にて開示することはしないでください.
- gen1_small10
- gen1_small12
- gen1_small13
- gen1_small14
- gen1_small15
- gen1_small17
- gen1_small18
- gen1_small19
- gen1_small20
断り書き
本問題で提供するデータは Oxford Nanopore Technologies 社の開発している PromethION DNA シークエンサーと,一般にはまだ販売されていないQ20試薬を用いた同社提供の(公開許諾済みの)ヒトゲノムデータから作成していますが,今回提供されたデータは開発中の試薬を用いているため今後製品として同製品の一般販売が開始された場合の製品の性能を示すものではありません.
問題の背景
※ この項目は読まなくても問題を解くことができますが,出題の背景となりますため,ご興味を持ってくださった方はお読みいただけると幸いです.
DNA の配列(A, C, G, T)を読み取る機械である DNA シークエンサーは染色体の端から端までを誤り無く読み取ることはできない.細胞からDNAを抽出する際に DNA が痛んでしまい,細かく千切れてしまうため,DNAシークエンサーのセンサー部分に全長の染色体をセットすることがそもそも不可能である.このため,現実世界では細かく千切れた DNA 断片の配列をたくさん読み取ってコンピューター処理により元々の DNA 配列を推定し復元する.読み取った DNA 配列は千切れているため,染色体のどの部分を読んだのかが分からず,染色体上のどこかランダムな位置から読まれた断片配列が読み取られる.

読み取った断片配列が染色体上のどこから読まれた配列であるかは,ヒトの場合にはヒト参照ゲノムと呼ばれる標準的なヒトゲノム配列に対してペアワイズアラインメントを行うことで調べている.概ね9割ぐらいのヒトDNA配列はほとんど全ての人類で同じような順序で並んでいる.つまり,ヒト参照配列にマッチングを行うことで染色体のどの部分から出てきた断片配列であるかが分かる,ということである.残りの1割は標準的なヒト参照ゲノム配列に対してマッチングする場所が2箇所以上あり,染色体上のどこから得られた断片なのかが確定できなかったり,標準的な参照ヒトゲノム配列にはそもそも存在しない配列だったりする.
今回のコンテストで提供するデータは匿名の複数の人物から「世界中にデータを公開しても良い」という条件で頂いた DNA を実際に PromethION シークエンサーと最新のQ20試薬で読んだ断片配列を用いて作成している.コンテスト参加者に配っているサンプルデータからジャッジに用いるデータが類推できないように,コンテスト参加者に配ったデータとジャッジに用いるヒト DNA断片配列は異なる人物から得られた DNA 配列断片である.以下のスクリーンショットは IGV と呼ばれるゲノム断片配列ビューアーを用いて実際のデータを表示している例である.

観測試行の (1) において 50% の確率で方向を選んでいるのは DNA の2重螺旋のうちどちら側が DNA シークエンサーによって読まれるかを模しており,基本的に現実世界でも 50% の確率で2重螺旋のどちら側が選ばれるかが決まると思われている.ただし,実際にそれが成り立っているかどうかは誰も知らない.読み取った断片配列を参照ヒトゲノム配列にマッチングさせた際に方向を揃える処理を行うことが一般的であり,上記のスクリーンショットでは参照ヒトゲノム配列の方向に合わせて断片配列の向きを全て揃えてある.
観測試行の (2) では DNA 断片の長さを決めている.実際の分布はDNA断片を細胞から抽出する際の実験条件等に依存して複雑な形をしており,具体的な分布を事前に示すことは難しい.
DNAシークエンサーで読み取り可能な断片配列長は技術の進歩とともにどんどん長くなり,2000年頃には 1200 文字(1200塩基対)程度だった最大読み取り長は,PromethION ではほぼ無限と言われている.ただし,DNA 断片配列を壊さずにシークエンサーにセットできた世界最長の記録は 400万文字(400万塩基対)程度と言われている.何れにせよ,DNAは通常もっとずっと短く千切れてしまっているので連続した読み取り長は 1,000 文字から10万文字ぐらいとなるのが普通である.
DNAシークエンサーの読み取りは完璧では無く,観測エラーが発生する.このため,DNAシークエンサーにセットした DNA の配列とは若干異なる配列が読み取られて出力されることが多い.エラーがどのようなメカニズムで発生してどのような性質(分布)を持っているのかは科学的な興味の対象である.今回提供した PromethION の Q20+試薬を用いたデータは Oxford Nanopore Technologies が開発した最新の試薬を使っているため,エラーの性質(分布)については未知の部分も多い.簡単に言うと出題者にも確かなことは言えない,ということである.旧バージョンの試薬では多くの(6文字以上)連続した
今回,参加者の皆様には参照ゲノム配列と PromethION の出力データの一部をお配りするので,新型試薬の観測エラー(シークエンシングエラー)の性質を推定し,2本の DNA 配列(ゲノム配列の一部)をなるべく正しく推定するプログラムを書いて欲しい.余談とはなるが,研究現場で最終的に達成したい精度は,エラーが 1,000,000 文字(塩基)につき 1塩基以下である.今回の問題で言えば全ての問題について満点に相当する.過去に行われた別のプログラミングコンテストでは,DNA 配列解析とは全く無縁のプログラマーが研究業界トップのプログラムを(コンテストで設定された基準で)超えるパフォーマンスをたたき出したと聞く.このコンテストでも業界トップの既知のアルゴリズムを超えるアルゴリズムが産まれたりはしないかと密かに期待をしているところである.Oxford Nanopore Technologies 社もおそらく同様の期待を抱いてのことだとは思うが, DNA 配列シークエンシングを行い本コンテストへのデータ提供を承諾してくれた.もしこの試みが上手く行けば PromethION を用いたゲノム解読が進歩して,がんの治療法やさまざまな遺伝病の原因発見が大きく加速するかも?