Time Limit: 4 sec / Memory Limit: 256 MiB
Problem
Alice has a box locked with n digits dial lock. Each dial of the lock can be set to a digit from 0 to 9. Unfortunately, she forgot the passcode (of n digits). Now she will try all possible combinations of digits to unlock the key.
She can do one of the following procedure each time.
- Choose 1 dial and add 1 to that digit. (If the digit chosen was 9, it will be 0).
- Choose 1 dial and subtract 1 from that digit. (If the digit chosen was 0, it will be 9).
Curiously, she wants to try all combinations even if she found the correct passcode during the trials. But it is a hard work to try all the 10^n combinations. Help her by showing the way how to make the procedure less as possible.
Initially, the combination of digits of the lock is set to 00..0.
Calculate m, the minimum number of procedures to try all combinations of digits, and show the m+1 combinations of digits after each procedures, including the initial combination 00..0. If there are more than one possible answer, you may choose any one of them.
Checking if the current combination of digits matches the passcode doesn't count as a procedure.
Input
Input is given in the following format.
n
- On the first line, you will be given n (1 \leq n \leq 5), the number of digits of the dial lock.
Output
On the first line, output m, the minimum number of procedures to try all combinations of digits.
On the following m+1 lines, output the combination of digits that appears during the trial in order. If there are more than 1 possible answer, you may choose any one of them. Make sure to insert a line break at the end of the last line.
Input Example 1
1
Output Example 1
9 0 1 2 3 4 5 6 7 8 9
Don't forget to output the minimum number of procedures 9 on the first line.
On the following lines, note that you have to output m+1 lines including the initial combination 0.
Input Example 2
2
Output Example 2
99 00 01 02 03 04 05 06 07 08 09 19 18 17 16 15 14 13 12 11 10 20 21 22 23 24 25 26 27 28 29 39 38 37 36 35 34 33 32 31 30 40 41 42 43 44 45 46 47 48 49 59 58 57 56 55 54 53 52 51 50 60 61 62 63 64 65 66 67 68 69 79 78 77 76 75 74 73 72 71 70 80 81 82 83 84 85 86 87 88 89 99 98 97 96 95 94 93 92 91 90
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
Let us define an strict total order relation between 2 distinct points P(x_1,y_1),Q(x_2,y_2) on a rectangular coordinate plane as following.
- If |x_1|+|y_1|\neq|x_2|+|y_2| and |x_1|+|y_1|<|x_2|+|y_2| then P<Q
- If |x_1|+|y_1|=|x_2|+|y_2| and x_1\neq{x_2} and x_1<x_2 then P<Q
- If |x_1|+|y_1|=|x_2|+|y_2| and x_1=x_2 and y_1<y_2 then P<Q
- If else, P>Q
Your task is to answer many queries that asks, "When you sort the set of all the integer lattice \mathbb{Z}^2 in ascending order by the relation defined above, output the n-th (1-indexed) element."
Input
Input is given in the following format
Q n_1 n_2 : n_Q
- On the first line, you will be given an integer Q (1 \leq Q \leq 100,000), the number of queries.
- On the following Q lines, each line contains the information of each query. The i-th (1 \leq i \leq Q) line consists of n_i (1 \leq n_i \leq 10^{18}), the number n of the i-th query.
Output
Output Q lines, each line containing the answer to each query in the order the queries appear in the input. Make sure to insert a line break at the end of the last line.
Input Example 1
7 1 2 3 4 5 6 1000000000000000000
Output Example 1
0 0 -1 0 0 -1 0 1 1 0 -2 0 263818038 443288743
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
You are given N points of integer lattice on a rectangular coordinate plane, You want to choose some points from them to make a regular polygon by connecting the chosen points with straight lines. Also, you want to choose as many points as possible to make a regular polygon.
Determine the points you should choose to make a regular polygon which has most vertices possible. If there are more than one possible answers, you may choose any one of them.
Input
Input is given in the following format.
N x_1 y_1 x_2 y_2 : x_N y_N
- On the first line, you will be given an integer N (1 \leq N \leq 1,000), the number of integer lattice points given.
- On the following N lines, you will be given the coordinates of each lattice. The i-th (1 \leq i \leq N) line consists of two integers x_i,y_i (-10^9 \leq x_i,y_i \leq 10^9), the x,y coordinate of the i-th lattice, respectively.
- Each given lattice is guaranteed to be distinct. In other words, for any 2 integers i,j(1 \leq i,j \leq N), if i \neq j then (x_i,y_i)≠(x_j,y_j) holds.
Output
On the first line, output m, the number of points you chose to make a regular polygon which has most vertices possible.
On the following m lines, output the index(1-indexed) of each points you chose in ascending order .
If you cannot make any regular polygon from the given points, just output a single line containing 0.
Input Example 1
6 1 0 -1 0 0 1 0 -1 1 2 -1 2
Output Example 1
4 1 2 3 4
Among the given 6 points, you can choose 4 points (1,0),(-1,0),(0,1),(0,-1) to make a regular square, which has the most vertex possible. So the answer is 4 and the indices of those points.
The 4 points (-1,0),(1,0),(1,2),(-1,2) can also make a regular square. So, the indices of them, {1,2,5,6}, will be considered correct too.
Input Example 2
4 0 0 1 0 2 0 3 0
Output Example 2
0
The given points are on a straight line. You cannot make any regular polygon from them.
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
There is a maze which has 1 start and 2 goals. The maze is made of H rows and W columns rectangular array of cells. Each cell is specified as start, goal, pathway, or an obstacle. Let (r, c) be the r-th row's, c-th cell from the left.
You will be given a map of the maze. You have to draw two paths from start cell to each goal cell in that map. A path is an array of cells that begins with start cell and ends with goal cell, contains no obstacle cell, and each pair of neighboring cells in the array is adjoining. A pair of cells (a, b) and (c, d) is adjoining if |a-c|+|b-d|=1. The paths you draw must fulfill the following conditions.
- Each path must contain the least possible number of cells. That means each path must be the shortest path from start to each goal.
- To make paths distinguishable, each path must not have any cell in common, except the start cell.
Determine if you can make the paths that meets the condition in the given maze, and show the paths in the maze if possible. Read the Input and Output section for the detailed format.
Input
H W
s_{(1,1)}s_{(1,2)}…s_{(1,W)}
s_{(2,1)}s_{(2,2)}…s_{(2,W)}
:
s_{(H,1)}s_{(H,2)}…s_{(1,W)}
-
On the first line, two integers H, W (1 \leq H, W \leq 50), the size of the maze is given.
-
On the following H lines, each line containing a string of length W, the map of the maze is given. The i-th (1 \leq i \leq H) line's j-th (1 \leq j \leq W) character represents the cell (i, j). Each character means as following.
.represents that the cell is a pathway cell.#represents that the cell is an obstacle cell.Srepresents that the cell is the start cell.Arepresents that the cell is the first goal cell.Brepresents that the cell is the second goal cell.
It is guaranteed that the character
S,A,Bappears only once. Also it is guaranteed that for each goal there's at least 1 path.
Output
If there are no paths to fulfill the conditions in the problem section, output 1 line containing NA.
If there are paths that fulfill the conditions, Output H lines that each line consists of W characters. The i-th (1 \leq i \leq H) line's j-th (1 \leq j \leq W) character in the output should represent the cell (i, j) in the maze. The output must fulfill the following conditions.
- The cell that was a pathway in the input must be one of
.,aorb. - The cell that was a start, an obstacle, or a goal cell in the input must be the same character as in the input.
- It should be able to reach the goal cell
Afrom the start cell by following the adjoiningacell. The number of cellamust be the least possible to reach the goal. - It should be able to reach the goal cell
Bfrom the start cell by following the adjoiningbcell. The number of cellbmust be the least possible to reach the goal.
In other words, show the path to each goal A, B by the characters a, b.
If there are more than one possible answers, you may choose any one of them.
Make sure to insert a line break at the end of the output.
Input Example 1
5 5 ..#.. .B.A# ...#. ..... ..S#.
Output Example 1
..#.. .BaA# .ba#. .ba.. .bS#.
Input Example 2
2 3 SBA ...
Output Example 2
NA
The goal cell is not an obstacle, so the shortest path to the goal A is only (1, 1) → (1, 2) → (1, 3).
However, that path contains the goal cell B and thus you cannot avoid to use the common cell in the shortest paths.
Therefore, you should output NA.
Input Example 3
5 5 ..#.. .B.A# .#.#. ..... ..S#.
Output Example 3
NA
Input Example 4
5 8 .#...#.. .#.#.#.. .S.#...B .#####A. ........
Output Example 4
.#bbb#.. .#b#b#.. aSb#bbbB a#####A. aaaaaaa.
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
There is a video game. In the game, there are N numbers of stages. There are 3 levels of difficulty and each stage has one of a difficulty in 1,2,3.
The number of stages of each difficulty is N_1,N_2,N_3 (N_1+N_2+N_3=N) For each difficulty, you know that the probability of completing the stage of that difficulty in one trial is P_1,P_2,P_3 (%).
You have to pay cost 1 to play the game. In one gameplay, you can play at least 1 stage, and at most 4 stages. The number of stages you can play with cost 1 depends as following.
- If you complete the first trial, you can continue to play the second trial. If you couldn't complete the first trial, that's the end of that play.
- If you complete the second trial, you can continue to play the final trial. If you couldn't complete the second trial, that's the end of that play.
- If you complete the final trial and also if the difficulty of that stage was 2 or 3, you can continue to play the extra trial. If not, that's the end of that play.
Before starting each first, second, final, and extra trial, you may choose any stage of any difficulty to play. Also, you may choose the stage you have already completed before.
For example, if you paid cost 1 and started the game, completed the first trial, and failed the second trial, that's the end of the play for that time. You can't play the final trial in that case.
Your aim is to complete all the N stages at least 1 time each. Regarding you followed a optimal strategy to minimize the total cost, calculate the expected value of cost you must pay to achieve that.
Whenever you choose the stage to play, you can choose any stage using the information about all stages you have tried including the stages you have completed at previous trial.
Input
Input is given in the following format.
N_1 N_2 N_3 P_1 P_2 P_3
- On the first line, you will be given three integers N_1,N_2,N_3 (0 \leq N_1,N_2,N_3 \leq 100), the number of stages of each difficulty separated by space, respectively.
- On the second line, you will be given three integers P_1,P_2,P_3 (1 \leq P_1,P_2,P_3 \leq 100), the probability of completing the stage of each difficulty in percentage separated by space, respectively.
Output
Output one line containing the expected value of cost you must pay to complete all stages when you followed the optimal strategy to minimize the total cost. Your answer is considered correct if it has an absolute or relative error less than 10^{-7}. Make sure to insert a line break at the end of the line.
Input Example 1
3 0 1 100 100 100
Output Example 1
1.0
There are 4 stages. you can surely complete the stage of any difficulty at once.
Pay cost 1 to start the gameplay. For each trial, choose the stage as following and you can complete all the stages with no additional cost.
- For the first trial, choose the stage of difficulty 1.
- For the second trial, choose the stage of difficulty 1.
- For the final trial, choose the stage of difficulty 3.
- For the extra trial, choose the stage of difficulty 1.
Input Example 2
100 100 100 100 100 100
Output Example 2
75.0
Input Example 3
3 0 1 50 100 50
Output Example 3
5.0
Input Example 4
4 1 1 50 25 10
Output Example 4
17.01875
Input Example 5
11 13 17 75 50 25
Output Example 5
69.106100438
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
There's a Japanese dish called 'Yakiniku', which is very similar to barbecue. You roast some pieces of meat on a grill to cook 'Yakiniku'.
You have a grill that can roast any number of pieces of meat on it at once. You want to make N pieces of 'Yakiniku' using that grill.
'Yakiniku' is a very tender dish that the i-th piece of meat must be put on the grill at the time s_i, and must be picked up at the time t_i sharp. If you pick the piece of meat later than t_i that piece is 'scorched'. If you pick the piece of meat earlier than t_i that piece is 'underdone'.
However, when you pick the i-th piece of meat at the time t_i, you totally forget where you put the i-th piece of meat on, so you pick 1 piece of meat from the grill at random. Calculate the probability of each piece of meat picked up 'underdone' and 'scorched'.
Input
Input is given in the following format.
N s_1 t_1 s_2 t_2 : s_N t_N
- On the first line, you will be given the integer N (1 \leq N \leq 100,000), the number of pieces of meat you are going to cook 'Yakiniku'.
- Following N lines consists of two integers s_i,t_i (0 \leq s_i < t_i \leq 10^9), the time you put the i-th meat on the grill and the time you have to pick up that meat from the grill. s_1,s_2,...,s_N,t_1,t_2,...,t_N are distinct from each other.
Output
Output N lines. The i-th (1 \leq i \leq N) line should contain the probability of i-th piece of meat picked up from the grill 'underdone' and 'scorched' separated by space. Your answer is considered correct if it has an absolute or relative error less than 10^{-7}.
Input Example 1
2 1 3 2 4
Output Example 1
0.0 0.5 0.5 0.0
Think of the 1st piece of meat. At the time 3 there are 2 pieces of meat on the grill. You pick the 2nd piece of meat with probability 1/2 and in that case at the time 4 the 1st meat will be picked up 'scorched'.
Think of the 2nd piece of meat. At the time 3 the 2nd piece of meat is taken from the grill with probability 1/2 and is 'underdone'.
Input Example 2
5 1 2 3 4 5 10 6 9 7 8
Output Example 2
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.6666666667 0.0000000000 0.3333333333 0.3333333333 0.0000000000 0.6666666667
Input Example 3
1 0 1000000000
Output Example 3
0 0
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
There is a 2-dimensional grid of size R \times C. There are many explosives warehouses on some of the cells.
When a warehouse catches fire, it finally explodes at some time in the future. When a warehouse explodes, it blasts in a + shape with fire extending on all four side. Blast fire extends until it reaches other warehouse. Blast fire won't reach the cells behind those warehouses.
A warehouse exposed to blast fire may catch fire or may not catch fire. A warehouse that once exposed to blast fire but didn't catch fire then, can be exposed to another blast fire. In that case, it's same as before, the warehouse may catch fire or may not catch fire.
An exploded warehouse won't catch fire anymore but still blocks the blast fire.
At first, you lit fire on one explosives warehouse. Finally, all warehouses had exploded.
During that disaster, no warehouses exploded at the same time. (Some of the warehouses could have caught fire at the same time.)
Calculate the number of possible ways of exploding that all warehouses explodes. As the answer can be rather large, print it as a remainder after dividing it by number 1000000009(10^9+9).
Ways of exploding is a set of pairs of warehouses. Each pair is a warehouse which caught fire and the warehouse which put fire on the former warehouse by exploding. When two ways of exploding have at least one different pair of warehouses, they are distinct.
Input
Input is given in the following format.
R C
s_{(1,1)}s_{(1,2)} .. s_{(1,C)}
s_{(2,1)}s_{(2,2)} .. s_{(2,C)}
:
s_{(R,1)}s_{(R,2)} .. s_{(R,C)}
a b
- On the first line you will be given two integers R,C (1 \leq R,C \leq 16) separated by space, the number of rows and columns of the grid, respectively.
- Following R lines is the place of warehouses.
Each line contains a string of size C. Each string consists of
.andW. The i-th (1 \leq i \leq R) line's j-th (1 \leq j \leq C) character represents the cell (i,j). If the character is., the cell (i,j) is an empty cell. If the character isW, a warehouse is on the cell (i,j). - On the next line, you will be given two integers a,b (1 \leq a \leq R,1 \leq b \leq C) separated by space. (a,b) is the place of the warehouse you first put fire on. It is guaranteed that there is a warehouse on this cell.
- It is guaranteed that there is at least 1 warehouse.
Output
Output one line containing the number of ways of exploding all warehouses modulo 1000000009. Make sure to insert a line break at the end of the output.
Input Example 1
3 4 W.W. .... W.W. 1 1
Output Example 1
4
For example, there is one way of exploding like below. Including this way, there are 4 ways of exploding.
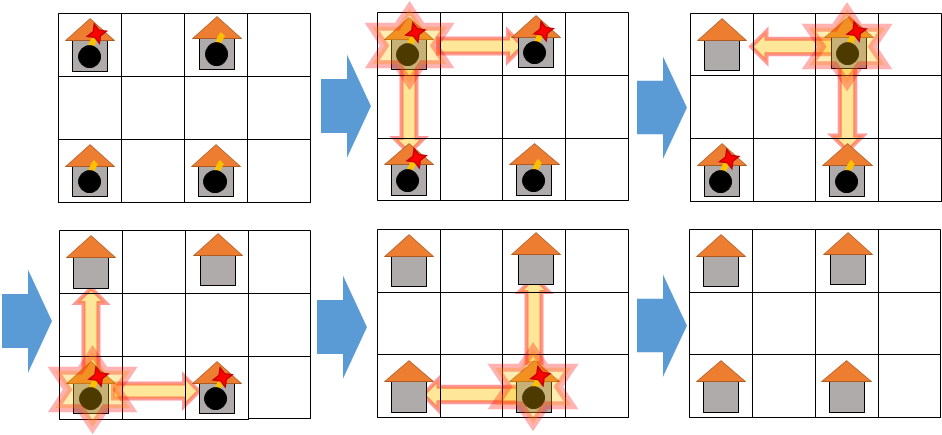
In this way, the warehouses at (1,3) and (3,1) caught fire from warehouse at (1,1), and the warehouse at (3,3) caught fire from warehouse of (3,1)
Input Example 2
3 4 W.W. .W.W W.W. 2 2
Output Example 2
0
Not all warehouses can explode in this case.
Input Example 3
1 1 W 1 1
Output Example 3
1
Input Example 4
16 16 WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW 1 1
Ouput Example 4
242986351
Don't forget to output the remainder after dividing the number by 1,000,000,009.
Time Limit: 5 sec / Memory Limit: 256 MiB
Problem
You are playing a video game. In this game there is a dungeon with N + 2 rooms placed on a straight line. Each room is numbered from 0 to N+1 in order. You can move from one room to a neighboring room. You are now at room No.0. Your goal is to reach room No.(N + 1) with least damage taken.
The room No.0 and No.(N + 1) are empty rooms. In each of the room from No.1 to No.N, there is an item or a monster. You are given N pairs of integers which tells the contents of each room respectively. For each i (1 \leq i \leq N), the integers A_i, B_i means as following.
- When A_i = 0, there is 1 key on which a booby-trap is set in the room No.i. If you pick up that key you take B_i points of damage from the trap. You may choose not to pick up the key, in which case you take no damage.
- When A_i = 1, there is 1 treasure box in the room No.i. In the treasure box there is a crystal that increases your DEF parameter by B_i points. You can consume 1 key to open the treasure box and increase your DEF. You may choose not to open the treasure box, in which case you don't consume a key, and keep your DEF parameter as is. Your initial DEF parameter is 0.
- When A_i = 2, there is a monster in the room No.i. You must fight that monster when you first entered that room, and take B_i - (\rm{player's\ DEF\ at\ that\ time}) points of damage. When you visit the room after that first battle, there is no monster in the room, and you take no damage.
You start from the room No.0. Calculate the least damage you take to reach the room No.(N + 1)
Note that you can go back to the room you have visited, and the damage taken from the booby-trap can't be decreased by your DEF parameter.
Input
N A_1 B_1 A_2 B_2 : A_N B_N
- On the first line, you will be given an integer N (1 \leq N \leq 900), which means the number of rooms in the dungeon is N + 2.
-
On the following N lines you will be given two integers A_i (0 \leq A_i \leq 2), B_i (0 \leq B_i \leq 10^9) separated by space, the information of each room. The i-th line tells the contents of the room No.i. These information are guaranteed to meet the following conditions.
- The number of each kind of rooms is less than 300.
- Even if you acquire all the crystals in the dungeon, the damage taken from a monster will not be less than 0. That means, let X the sum of B_i for all i which satisfies A_i = 1. For any j which satisfies A_j = 2, B_j \geq X holds.
Output
Output a single line containing the least damage you take to reach the room No.(N + 1) starting from the room No.0. Make sure to insert a line break at the end of the output.
Input Example 1
4 1 2 2 3 0 1 2 2
Output Example 1
4
Optimal move is as following.
- At first go to room No.3 and take the key. On the way, you take 3 points of damage from the monster in the room No.2, and 1 point of damage from a booby-trap at the room No.3.
- Next, go back to room No.1, open the treasure box, increase your DEF by 2 points. On this way you pass the room No.2, but you have already beaten the monster so you take no damage.
- Finally go to the goal, room No.5. On this way you fight the monster at the room No.4, but thanks to your 2 points of DEF parameter, you take 0 points of damage.
Input Example 2
4 1 2 2 3 0 4 2 2
Output Example 2
5
This case is similar to the Example 1, but the damage from the booby-trap is large so the optimal move is to ignore the key.
Input Example 3
7 0 4 1 3 2 10 1 6 2 9 0 5 2 10
Output Example 3
21
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
There is a two-dimensional grid of N \times N cells. Let (r, c) be the r-th row's c-th cell from the left. Some of these cells are painted black, other cells are painted white.
At first you are at (1, 1), and you want to go to (N, N). However, there's a stranger Mr.X trying to obstruct your way to (N, N).
You and Mr.X move in turns. At the beginning Mr.X starts the move. On each move each person can move as following.
- Mr.X moves to one of the white cell adjoining to the cell where you are. If there is no cell Mr.X can move to, Mr.X disappears from the grid for that turn.
- You can move to one of the cells adjoining to the cell where you are, which Mr.X didn't move to in his last turn.
In other words, you can move to one of the adjoining cell. But before your move Mr.X choose one of the possible move and block that. However, Mr.X can't block your move to a black cell.
You will be given the color of each cell. Determine if you can reach (N, N) no matter how Mr.X obstructs your way.
Input
N
s_{(1,1)}s_{(1,2)}…s_{(1,N)}
s_{(2,1)}s_{(2,2)}…s_{(2,N)}
:
s_{(N,1)}s_{(N,2)}…s_{(1,N)}
- On the first line you will be given an integer N (2 \leq N \leq 1,000), the size of the grid.
- Following N lines shows the color of each cell. Each line consists of
.and#. The i-th (1 \leq i \leq N) row's j-th (1 \leq j \leq N) character represents the color of (i, j). When the character is., (i, j) is painted white. When the character is#, (i, j) is painted black.
Output
If you can reach (N, N) no matter how Mr.X obstructs the way, output YES.
If not, output NO.
(Both without the period.)
Make sure to insert a line break at the end of the output.
Input Example 1
4 ..## ...# #..# ####
Output Example 1
YES
If Mr.X blocks (1, 2) at his first move, you can move to (2, 1). After that you can follow the black cells to reach (4, 4).
If Mr.X blocks (2, 1) you can move to (1, 2) and then follow the black cells to reach (4, 4).
Therefore, you can reach (4, 4) notwithstanding Mr.X's obstruction. The answer is YES.
Input Example 2
4 ..## .... #..# ####
Output Example 2
NO
In this case, when you are at (1, c), Mr.X can block (2, c). If Mr.X follows this optimal strategy for him, you can't reach (4, 4).
The answer is NO.
Input Example 3
2 .# #.
Output Example 3
NO
In this case, Mr.X can block (2,2).
Time Limit: 4 sec / Memory Limit: 256 MiB
Problem
Yu loves bitwise AND operation and big number. Yu's friend Yihuo loves bitwise XOR operation and small number. They are good friends that whenever someone sends them an array of numbers as a gift, they share the numbers with each other.
For an array of non-negative integers p_1, p_2, ..., p_k, let D be the result of bitwise AND between all numbers in the array (p_1\rm{\ AND\ }p_2\rm{\ AND\ }...\rm{\ AND\ }p_k), and let X be the result of bitwise XOR between all numbers in the array (p_1\rm{\ XOR\ }p_2\rm{\ XOR\ }...\rm{\ XOR\ }p_k). Yu's satisfaction value for p_1, p_2, ..., p_k is D, Yihuo's satisfaction value for the same array of numbers is -X (Note that Yihuo loves small number. The less X is, the more Yihuo satisfies.)
Whenever they receive an array of non-negative integer p_1, p_2, ..., p_k as a gift, they cut the array in the middle and Yu gets the former part, Yihuo gets the latter part. The place they cut the array is determined to maximize the sum of each satisfaction value for the array each get. To say more precisely, they cut the array at after the i-th number within 1 \leq i < k, which maximizes the sum of Yu's satisfaction value for p_1, p_2, ..., p_i and Yihuo's satisfaction value for p_{i+1}, p_{i+2}, ..., p_k.
You will be given a N elements non-negative integer array A and Q numbers of query. The j-th query asks "How much is the sum of their satisfaction value when we give A_{l_j}, A_{l_j+1}, ..., A_{r_j} to Yu and Yihuo". Your task is to answer all queries in the given order.
Note that each query is described by 2 integers l_j, r_j (1 \leq l_j < r_j \leq N), but those integers are not given directly. You must calculate those 2 integers from the last query's answer as described in the Input section. This means that you must calculate the answer of queries in the given order.
Input
N Q A_1 A_2 ... A_N l'_1 r'_1 l'_2 r'_2 : l'_Q r'_Q
- On the first line, you will be given two integers N (2 \leq N \leq 10^5), Q (1 \leq Q \leq 10^5) separated by space, the number of elements in the array A and the number of queries respectively.
- On the second line, you will be given N integers separated by space. The i-th (1 \leq i \leq N) integer is A_i (0 \leq A_i < 2^{31}).
- Following Q lines are the information of the query. The j-th (1 \leq j \leq Q) line contains 2 integers l'_j (1 \leq l'_j \leq N), r'_j (1 \leq r'_j \leq N) separated by space.
Calculate l_j, r_j, the exact integers in the query as following.
- l_1 = l'_1, r_1 = r'_1
-
For all j that satisfies 2 ≦ j ≦ Q, let m_{j - 1} be the answer to the (j - 1)-th query.
- l_j = ((l'_j + \|m_{j - 1}\|)\rm{\ MOD\ }N) + 1
- r_j = ((r'_j + \|m_{j - 1}\|)\rm{\ MOD\ }N) + 1
Note that each answer may be a negative number that the absolute value of m_{j - 1} is used to obtain l_j and r_j. It is guaranteed that 1 \leq l_j < r_j \leq N holds.
Output
Output Q lines. The j-th (1 \leq j \leq Q) line should contain the answer to the j-th query. Make sure to insert a line break at the end of the output.
Input Example 1
7 4 7 3 5 4 6 3 1 2 5 2 5 3 4 5 1
Output Example 1
-1 2 2 5
The answer to each query is as following.
- For the first query, l_1 = 2, r_1 = 5. The array of numbers 3, 5, 4, 6 will be separated to 3, 5 and 4, 6, which provides Yu's satisfaction value 3 AND 5 = 1, Yihuo's satisfaction value -(4 XOR 6) = -2, summed up to -1.
- For the second query, l_2 = (2 + \|-1\|) MOD 7 + 1 = 4, r_2 = (5 + \|-1\|) MOD 7 + 1 = 7. The array 4, 6, 3, 1 will be separated to 4, 6 and 3, 1, which provides Yu's satisfaction value 4 AND 6 = 4 and Yihuo's satisfaction value -(3 XOR 1) = -2, summed up to 2.
- For the third query, l_3 = (3 + \|2\|) MOD 7 + 1 = 6, r_3 = (4 + \|2\|) MOD 7 + 1 = 7. The array 3, 1 can only be separated to 3 and 1, which provides Yu's satisfaction value 3 and Yihuo's satisfaction value -1, summed up to 2.
- For the fourth query, l_4 = (5 + \|2\|) MOD 7 + 1 = 1, r_4 = (1 + \|2\|) MOD 7 + 1 = 4. The array 7, 3, 5, 4 will be separated to 7 and 3, 5, 4, which provides Yu's satisfaction value 7 and Yihuo's satisfaction value -(3 XOR 5 XOR 4) = -2, summed up to 5.
Input Example 2
20 30 1 4 3 6 9 9 6 7 5 3 5 4 9 4 1 2 14 5 11 1 14 18 4 15 2 10 3 13 20 15 7 12 18 10 9 15 20 12 5 7 6 10 8 12 4 14 17 11 15 16 17 7 20 13 8 9 14 17 13 16 5 6 4 11 5 7 4 6 12 16 16 15 13 16 2 7 8 15 10 16
Output Example 2
-4 -1 0 -2 -1 -4 -1 4 3 -1 3 -2 6 3 10 5 1 -2 -1 -5 1 -6 -4 -1 -4 0 -9 4 3 2
The l_i, r_i for each query is as following.
14 18 9 20 4 12 4 14 3 18 9 14 3 15 11 17 5 17 9 11 8 12 12 16 7 17 4 18 19 20 8 18 6 19 10 11 17 20 15 18 11 12 6 13 12 14 9 11 14 18 1 20 14 17 12 17 13 20 14 20