Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1500 点
問題文
N 頂点の連結な無向グラフがあり、頂点には 1~N の番号が付いています。 辺の長さはすべて 1 です。 各 i (1≦i≦N) について、頂点 1 と頂点 i の距離が A_i、頂点 2 と頂点 i の距離が B_i であることが分かっています。 このようなグラフが存在するかを判定してください。また、存在する場合は、辺の本数として考えられる最小値を求めてください。
制約
- 2≦N≦10^5
- 0≦A_i,B_i≦N-1
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 : A_N B_N
出力
条件を満たすグラフが存在する場合は辺の本数の最小値を、存在しない場合は -1 を出力せよ。
入力例 1
4 0 1 1 0 1 1 2 1
出力例 1
4
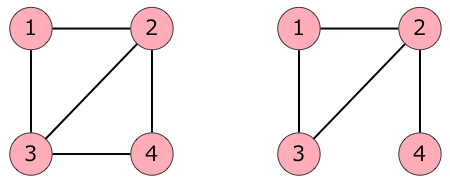
下図のような 2 種類のグラフが考えられますが、右のグラフの方が辺の本数が少ないです。
入力例 2
3 0 1 1 0 2 2
出力例 2
-1
このようなグラフは存在しません。
Score : 1500 points
Problem Statement
There is an undirected connected graph with N vertices numbered 1 through N. The lengths of all edges in this graph are 1. It is known that for each i (1≦i≦N), the distance between vertex 1 and vertex i is A_i, and the distance between vertex 2 and vertex i is B_i. Determine whether there exists such a graph. If it exists, find the minimum possible number of edges in it.
Constraints
- 2≦N≦10^5
- 0≦A_i,B_i≦N-1
Input
The input is given from Standard Input in the following format:
N A_1 B_1 A_2 B_2 : A_N B_N
Output
If there exists a graph satisfying the conditions, print the minimum possible number of edges in such a graph. Otherwise, print -1.
Sample Input 1
4 0 1 1 0 1 1 2 1
Sample Output 1
4
The figure below shows two possible graphs. The graph on the right has fewer edges.

Sample Input 2
3 0 1 1 0 2 2
Sample Output 2
-1
Such a graph does not exist.
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1500 点
問題文
高橋王国の通貨の単位は「ミョン」です。 高橋王国では、10 冪 (1, 10, 100, 1000, ...) ミョンの硬貨が用いられています。
エキシビ商店では N 個の品物が売られています。 商品 i (1≦i≦N) の値段は A_i ミョンです。
高橋くんはエキシビ商店に行き、N 個の商品のうち 1 個以上 N 個以下の商品を選んで買おうとしています。 高橋くんはお釣りが嫌いなので、どのように買い物をしてもお釣りが出ないように、財布の中に入れる硬貨を選びたいと思っています。 また、財布が重くなるのも困るので、硬貨の枚数をできるだけ少なくしたいと思っています。
このとき、高橋くんが財布に入れる必要のある硬貨の枚数の最小値を求めて下さい。ただし、財布に入れるための硬貨が足りなくなることは無いものとします。
制約
- 1≦N≦20,000
- 1≦A_i≦10^{12}
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 ... A_N
出力
どのように買い物をしてもお釣りが出ないように財布の中に入れる必要のある硬貨の枚数の最小値を出力せよ。
入力例 1
3 43 24 37
出力例 1
16
支払う金額として考えられるものは、24, 37, 43, 61, 67, 80, 104 の 7 通りです。 1 ミョン硬貨が 7 枚、10 ミョン硬貨が 8 枚、100 ミョン硬貨が 1 枚あれば、これらをお釣りなく支払うことが出来ます。
入力例 2
5 49735011221 970534221705 411566391637 760836201000 563515091165
出力例 2
105
Score : 1500 points
Problem Statement
The currency used in Takahashi Kingdom is Myon. There are 1-, 10-, 100-, 1000- and 10000-Myon coins, and so forth. Formally, there are 10^n-Myon coins for any non-negative integer n.
There are N items being sold at Ex Store. The price of the i-th (1≦i≦N) item is A_i Myon.
Takahashi is going to buy some, at least one, possibly all, of these N items. He hates receiving change, so he wants to bring coins to the store so that he can pay the total price without receiving change, no matter what items he chooses to buy. Also, since coins are heavy, he wants to bring as few coins as possible.
Find the minimum number of coins he must bring to the store. It can be assumed that he has an infinite supply of coins.
Constraints
- 1≦N≦20,000
- 1≦A_i≦10^{12}
Input
The input is given from Standard Input in the following format:
N A_1 A_2 ... A_N
Output
Print the minimum number of coins Takahashi must bring to the store, so that he can pay the total price without receiving change, no matter what items he chooses to buy.
Sample Input 1
3 43 24 37
Sample Output 1
16
There are seven possible total prices: 24, 37, 43, 61, 67, 80, and 104. With seven 1-Myon coins, eight 10-Myon coins and one 100-Myon coin, Takahashi can pay any of these without receiving change.
Sample Input 2
5 49735011221 970534221705 411566391637 760836201000 563515091165
Sample Output 2
105