実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
縦 N 行、横 N 列のグリッドがあります。上から r 行目、左から c 列目のマスをマス (r,c) と表します。各マスは黒か白で塗られており、マス (r,c) は S_{r,c} が # のとき黒で、 S_{r,c} が . のとき白で塗られています。
このグリッドに対して Q 個の質問が与えられるので、それぞれについて答えを求めてください。 i 番目 (1\le i\le Q) の質問では整数 U_i,D_i,L_i,R_i が与えられるので、以下の質問の答えを求めてください。
- U_i \le r \le D_i かつ L_i \le c \le R_i を 満たさない マスを全て黒で塗った後、以下の操作を最大で何回できるか求めてください。
- マス (r,c),(r,c+1),(r+1,c),(r+1,c+1) が全て白で塗られているような整数の組 (r,c) を選び、これら 4 つのマスのうち 1 つを黒で塗る。
各質問について独立に解いてください。言い換えると、各マスの色は質問のたびにはじめの状態にリセットされます。
制約
- 2\le N\le 500
- 1\le Q\le 2\times 10^5
- S_{r,c} は
.または# - 1\le U_i < D_i \le N
- 1\le L_i < R_i \le N
- N,Q,U_i,D_i,L_i,R_i は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q
S_{1,1}S_{1,2}\ldots S_{1,N}
S_{2,1}S_{2,2}\ldots S_{2,N}
\vdots
S_{N,1}S_{N,2}\ldots S_{N,N}
U_1 D_1 L_1 R_1
U_2 D_2 L_2 R_2
\vdots
U_Q D_Q L_Q R_Q
出力
Q 行出力せよ。
i 行目 (1\le i\le Q) には、 i 番目の質問に対する答えを出力せよ。
入力例 1
5 4 ..#.# ..... #.... ...#. .#... 1 3 1 3 3 5 3 5 2 3 1 4 1 5 1 5
出力例 1
2 0 2 5
1 番目の質問について考えます。
1\le r\le 3 かつ 1\le c\le 3 を満たさないようなマスを全て黒で塗ると、グリッドは以下のようになります。
..### ...## #..## ##### #####
このグリッドに対して以下のように 2 回操作を行うことができます。
- (r,c)=(1,1) を選ぶ。マス (1,1),(1,2),(2,1),(2,2) の中からマス (1,2) を選び、黒で塗る。
- (r,c)=(2,2) を選ぶ。マス (2,2),(2,3),(3,2),(3,3) の中からマス (2,2) を選び、黒で塗る。
2 回より多く操作をすることはできないので、 1 行目には 2 を出力してください。
入力例 2
7 6 #.#.... .....#. ....... .#..#.# #....#. ....... ....##. 1 3 2 7 4 6 1 6 6 7 2 7 3 5 4 6 1 6 2 4 1 7 1 7
出力例 2
4 4 2 0 6 13
Score : 400 points
Problem Statement
There is a grid with N rows and N columns. Let (r,c) denote the cell at the r-th row from the top and c-th column from the left. Each cell is colored black or white. Cell (r,c) is colored black when S_{r,c} is #, and white when S_{r,c} is ..
You are given Q questions about this grid, so answer each of them. In the i-th question (1\le i\le Q), integers U_i,D_i,L_i,R_i are given, so find the answer to the following question.
- After coloring all cells that do not satisfy U_i \le r \le D_i and L_i \le c \le R_i black, find the maximum number of times you can perform the following operation.
- Choose a pair of integers (r,c) such that cells (r,c),(r,c+1),(r+1,c),(r+1,c+1) are all colored white, and color one of these four cells black.
Solve each question independently. In other words, the color of each cell is reset to the initial state for each question.
Constraints
- 2\le N\le 500
- 1\le Q\le 2\times 10^5
- S_{r,c} is
.or#. - 1\le U_i < D_i \le N
- 1\le L_i < R_i \le N
- N,Q,U_i,D_i,L_i,R_i are all integers.
Input
The input is given from Standard Input in the following format:
N Q
S_{1,1}S_{1,2}\ldots S_{1,N}
S_{2,1}S_{2,2}\ldots S_{2,N}
\vdots
S_{N,1}S_{N,2}\ldots S_{N,N}
U_1 D_1 L_1 R_1
U_2 D_2 L_2 R_2
\vdots
U_Q D_Q L_Q R_Q
Output
Output Q lines.
The i-th line (1\le i\le Q) should contain the answer to the i-th question.
Sample Input 1
5 4 ..#.# ..... #.... ...#. .#... 1 3 1 3 3 5 3 5 2 3 1 4 1 5 1 5
Sample Output 1
2 0 2 5
Consider the first question.
After coloring all cells that do not satisfy 1\le r\le 3 and 1\le c\le 3 black, the grid becomes as follows.
..### ...## #..## ##### #####
You can perform the operation twice on this grid as follows.
- Choose (r,c)=(1,1). Among cells (1,1),(1,2),(2,1),(2,2), choose cell (1,2) and color it black.
- Choose (r,c)=(2,2). Among cells (2,2),(2,3),(3,2),(3,3), choose cell (2,2) and color it black.
You cannot perform the operation more than twice, so output 2 on the first line.
Sample Input 2
7 6 #.#.... .....#. ....... .#..#.# #....#. ....... ....##. 1 3 2 7 4 6 1 6 6 7 2 7 3 5 4 6 1 6 2 4 1 7 1 7
Sample Output 2
4 4 2 0 6 13
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
頂点に 1 から N の番号がついた N 頂点の完全グラフがあります。各辺は黒か白で塗られており、 i=1,2,\ldots,M に対し頂点 U_i と頂点 V_i を結ぶ辺は黒で、これら以外の辺は白で塗られています。
あなたは以下の操作を 0 回以上何回でも行うことができます。
- 1\le a < b < c \le N を満たす整数の組 (a,b,c) を選び、以下の 3 本の辺のそれぞれの色を白ならば黒に、黒ならば白に塗り直す。
- 頂点 a と頂点 b を結ぶ辺
- 頂点 b と頂点 c を結ぶ辺
- 頂点 a と頂点 c を結ぶ辺
あなたが適切に操作をしたとき、黒で塗られた辺を最大で何本にできるか求めてください。
制約
- 3\le N\le 2\times 10^5
- \displaystyle 0\le M\le 2\times 10^5
- 1\le U_i < V_i \le N
- (U_i , V_i) \neq (U_j , V_j) (i \neq j)
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 U_2 V_2 \vdots U_M V_M
出力
答えを出力せよ。
入力例 1
4 1 1 2
出力例 1
5
以下のように 2 回の操作を行うことで、黒で塗られた辺の本数を 5 本にすることができます。
- (a,b,c)=(1,3,4) を選ぶ。黒で塗られた辺は以下の 4 本になる。
- 頂点 1 と頂点 2 を結ぶ辺
- 頂点 1 と頂点 3 を結ぶ辺
- 頂点 1 と頂点 4 を結ぶ辺
- 頂点 3 と頂点 4 を結ぶ辺
- (a,b,c)=(2,3,4) を選ぶ。黒で塗られた辺は以下の 5 本になる。
- 頂点 1 と頂点 2 を結ぶ辺
- 頂点 1 と頂点 3 を結ぶ辺
- 頂点 1 と頂点 4 を結ぶ辺
- 頂点 2 と頂点 3 を結ぶ辺
- 頂点 2 と頂点 4 を結ぶ辺
黒で塗られた辺の本数を 5 本より多くすることはできないので、 5 を出力してください。
入力例 2
7 3 1 2 2 3 3 6
出力例 2
20
入力例 3
123123 0
出力例 3
7579575003
オーバーフローに注意してください。
Score : 500 points
Problem Statement
There is a complete graph with N vertices numbered 1 to N. Each edge is colored black or white. For i=1,2,\ldots,M, the edge connecting vertices U_i and V_i is colored black, and all other edges are colored white.
You can perform the following operation zero or more times.
- Choose a triple of integers (a,b,c) satisfying 1\le a < b < c \le N, and repaint each of the following three edges: white to black, black to white.
- The edge connecting vertices a and b
- The edge connecting vertices b and c
- The edge connecting vertices a and c
Find the maximum number of edges that can be colored black when you perform operations appropriately.
Constraints
- 3\le N\le 2\times 10^5
- \displaystyle 0\le M\le 2\times 10^5
- 1\le U_i < V_i \le N
- (U_i , V_i) \neq (U_j , V_j) (i \neq j)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M U_1 V_1 U_2 V_2 \vdots U_M V_M
Output
Output the answer.
Sample Input 1
4 1 1 2
Sample Output 1
5
By performing two operations as follows, you can make the number of black edges 5.
- Choose (a,b,c)=(1,3,4). Then, we have the following four black edges.
- The edge connecting vertices 1 and 2
- The edge connecting vertices 1 and 3
- The edge connecting vertices 1 and 4
- The edge connecting vertices 3 and 4
- Choose (a,b,c)=(2,3,4). Then, we have the following five black edges.
- The edge connecting vertices 1 and 2
- The edge connecting vertices 1 and 3
- The edge connecting vertices 1 and 4
- The edge connecting vertices 2 and 3
- The edge connecting vertices 2 and 4
You cannot make the number of black edges more than 5, so output 5.
Sample Input 2
7 3 1 2 2 3 3 6
Sample Output 2
20
Sample Input 3
123123 0
Sample Output 3
7579575003
Be careful about overflow.
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
数直線上に N 人の人がいます。
人 i (1\le i\le N) は最初座標 S_i にいますが、最終的に座標 T_i に移動したいと考えています。ここで、 S_1,S_2,\ldots,S_N,T_1,T_2,\ldots,T_N は全て相異なることが保証されます。
あなたは (1,2,\ldots,N) の順列 P=(P_1,P_2,\ldots,P_N) を一つ決め、 N 回の操作を順に行います。 i 回目 (1\le i\le N) の操作では、人 P_i を座標 S_{P_i} から座標 T_{P_i} まで数直線上の最短経路に沿って移動させます。ただし、移動経路上に他の人がいる場合喧嘩が発生します。
喧嘩が一度も発生しないような P が存在するか判定し、存在する場合は一つ求めてください。
制約
- 1\le N\le 2\times 10^5
- 1\le S_i, T_i \le 10^9
- S_1,S_2,\ldots,S_N,T_1,T_2,\ldots,T_N は全て相異なる
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N S_1 T_1 S_2 T_2 \vdots S_N T_N
出力
喧嘩が一度も発生しないような P が存在しない場合は No を出力せよ。
そうでない場合、喧嘩が一度も発生しないような P を以下の形式で出力せよ。
Yes P_1 P_2 \ldots P_N
条件を満たす P が複数ある場合、どれを出力しても正答となる。
入力例 1
4 1 3 2 4 7 5 8 10
出力例 1
Yes 3 2 1 4
P=(3,2,1,4) とすると、 N 回の操作は以下のように進みます。
- 1 回目:人 3 を座標 7 から座標 5 に移動させる。他の 3 人は座標 1,2,8 にいるため、喧嘩は発生しない。
- 2 回目:人 2 を座標 2 から座標 4 に移動させる。他の 3 人は座標 1,5,8 にいるため、喧嘩は発生しない。
- 3 回目:人 1 を座標 1 から座標 3 に移動させる。他の 3 人は座標 4,5,8 にいるため、喧嘩は発生しない。
- 4 回目:人 4 を座標 8 から座標 10 に移動させる。他の 3 人は座標 3,4,5 にいるため、喧嘩は発生しない。
したがって、 P=(3,2,1,4) を出力すると正答となります。
この他にも、例えば P=(4,3,2,1),(2,1,3,4) などを出力しても正答となります。
入力例 2
2 1 3 4 2
出力例 2
No
喧嘩が一度も発生しないような P は存在しません。したがって、 No を出力してください。
入力例 3
5 19 17 1 10 9 14 3 11 8 13
出力例 3
Yes 3 5 1 4 2
Score : 600 points
Problem Statement
There are N people on a number line.
Person i (1\le i\le N) is initially at coordinate S_i, and wants to eventually move to coordinate T_i. It is guaranteed that S_1,S_2,\ldots,S_N,T_1,T_2,\ldots,T_N are all distinct.
You fix one permutation P=(P_1,P_2,\ldots,P_N) of (1,2,\ldots,N) and perform N operations in order. In the i-th operation (1\le i\le N), you move person P_i from coordinate S_{P_i} to coordinate T_{P_i} along the shortest path on the number line. However, if there is another person on the movement path, a fight occurs.
Determine if there exists a P such that no fight occurs, and if it exists, find one.
Constraints
- 1\le N\le 2\times 10^5
- 1\le S_i, T_i \le 10^9
- S_1,S_2,\ldots,S_N,T_1,T_2,\ldots,T_N are all distinct.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N S_1 T_1 S_2 T_2 \vdots S_N T_N
Output
If there is no P such that no fight occurs, output No.
Otherwise, output a P such that no fight occurs in the following format.
Yes P_1 P_2 \ldots P_N
If there are multiple P that satisfy the condition, any of them will be accepted.
Sample Input 1
4 1 3 2 4 7 5 8 10
Sample Output 1
Yes 3 2 1 4
If P=(3,2,1,4), then the N operations proceed as follows.
- 1st operation: Move person 3 from coordinate 7 to coordinate 5. The other three people are at coordinates 1,2,8, so no fight occurs.
- 2nd operation: Move person 2 from coordinate 2 to coordinate 4. The other three people are at coordinates 1,5,8, so no fight occurs.
- 3rd operation: Move person 1 from coordinate 1 to coordinate 3. The other three people are at coordinates 4,5,8, so no fight occurs.
- 4th operation: Move person 4 from coordinate 8 to coordinate 10. The other three people are at coordinates 3,4,5, so no fight occurs.
Therefore, outputting P=(3,2,1,4) will be accepted.
Other acceptable outputs include P=(4,3,2,1),(2,1,3,4).
Sample Input 2
2 1 3 4 2
Sample Output 2
No
There is no P such that no fight occurs. Therefore, output No.
Sample Input 3
5 19 17 1 10 9 14 3 11 8 13
Sample Output 3
Yes 3 5 1 4 2
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
頂点に 1 から N までの番号がついた N 頂点の根付き木が与えられます。頂点 1 が根で、頂点 i (2 \le i \le N) の親は頂点 p_i (1\le p_i < i) です。はじめ、全ての頂点は白で塗られています。
あなたは以下の一連の操作を 0 回以上何回でも行うことができます。
- 以下の条件を全て満たす整数の組 (u,v) を選ぶ。
- 1\le u < v \le N
- 頂点 u と頂点 v はどちらも白で塗られている。
- u は v の祖先 ではない。
- 頂点 u と頂点 v を黒で塗る。
ただし、「u は v の祖先ではない」とは頂点 v から今いる頂点の親に移動する操作を何回行っても頂点 u に到達できないことを意味します。
あなたが適切な順序で操作を行ったとき、最大で何回操作ができるか求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1\le T\le 5\times 10^4
- 2\le N\le 5\times 10^5
- 1\le p_i < i
- 全てのテストケースにおける N の総和は 5\times 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケース \text{case}_i は以下の形式で与えられる。
N p_2 p_3 \ldots p_N
出力
T 行出力せよ。
i 行目 (1\le i\le T) には i 番目のテストケースについての答えを出力せよ。
入力例 1
4 6 1 2 2 2 5 7 1 2 3 4 5 6 7 1 2 3 4 2 4 12 1 1 2 2 2 4 4 4 7 7 7
出力例 1
2 0 2 5
1 番目のテストケースについて考えます。
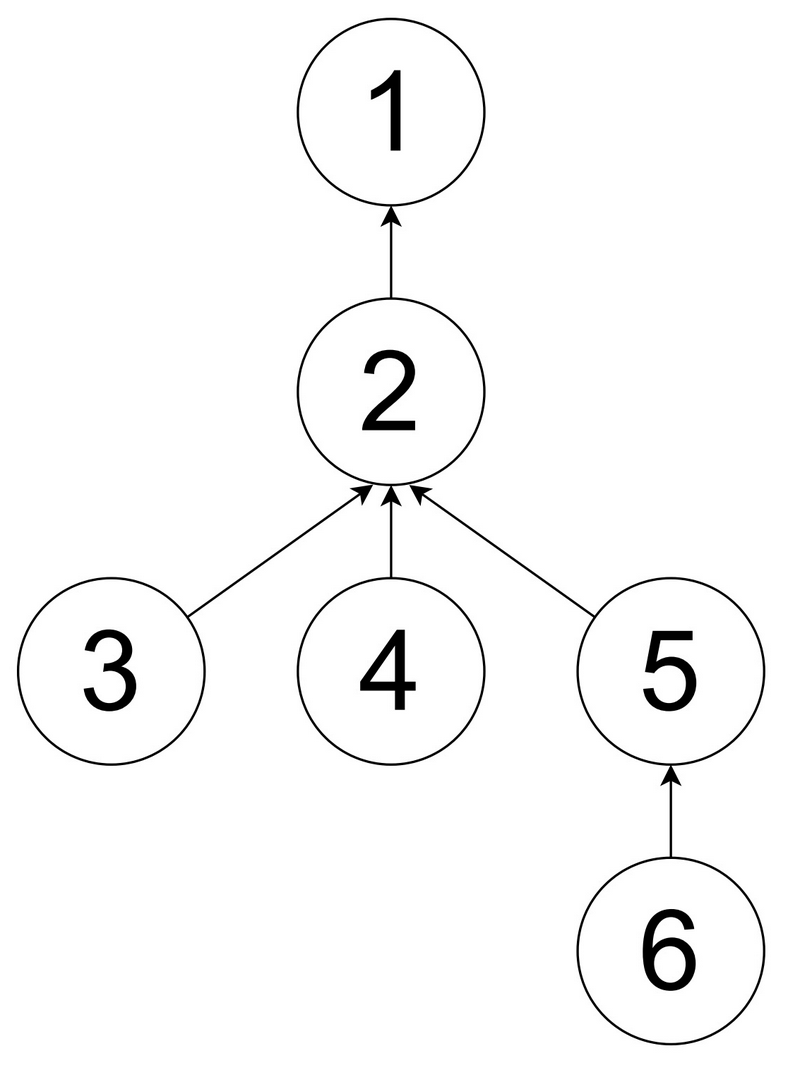
以下のように 2 回操作を行うことができます。
- (u,v)=(3,5) を選ぶ。頂点 3 と頂点 5 を黒で塗る。
- (u,v)=(4,6) を選ぶ。頂点 4 と頂点 6 を黒で塗る。
操作を 2 回より多く行うことはできないので、 1 行目には 2 を出力してください。
Score : 600 points
Problem Statement
You are given a rooted tree with N vertices numbered from 1 to N. Vertex 1 is the root, and the parent of vertex i (2 \le i \le N) is vertex p_i (1\le p_i < i). Initially, all vertices are colored white.
You can perform the following sequence of operations zero or more times.
- Choose a pair of integers (u,v) that satisfies all of the following conditions.
- 1\le u < v \le N
- Both vertices u and v are colored white.
- u is not an ancestor of v.
- Color vertices u and v black.
Here, "u is not an ancestor of v" means that you cannot reach vertex u from vertex v no matter how many times you perform the operation of moving to the parent of the current vertex.
Find the maximum number of operations you can perform when you perform operations in an appropriate order.
You are given T test cases, so find the answer for each of them.
Constraints
- 1\le T\le 5\times 10^4
- 2\le N\le 5\times 10^5
- 1\le p_i < i
- The sum of N over all test cases is at most 5\times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case \text{case}_i is given in the following format:
N p_2 p_3 \ldots p_N
Output
Output T lines.
The i-th line (1\le i\le T) should contain the answer for the i-th test case.
Sample Input 1
4 6 1 2 2 2 5 7 1 2 3 4 5 6 7 1 2 3 4 2 4 12 1 1 2 2 2 4 4 4 7 7 7
Sample Output 1
2 0 2 5
Consider the first test case.

You can perform two operations as follows.
- Choose (u,v)=(3,5). Color vertices 3 and 5 black.
- Choose (u,v)=(4,6). Color vertices 4 and 6 black.
You cannot perform more than two operations, so output 2 on the first line.
実行時間制限: 6 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
長さ N の非負整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
k=1,2,\ldots,N に対し以下の問題を解いてください。
- A_i と A_k のビット単位 \mathrm{OR} 演算が A_k となるような 1 以上 k 以下の整数 i 全てに対する A_i の 総積 を 998244353 で割ったあまりを求めてください。
ビット単位 \mathrm{OR} 演算とは
非負整数 X,Y のビット単位 \mathrm{OR}、X\ \mathrm{OR}\ Y は以下のように定義されます。
- X\ \mathrm{OR}\ Y を二進表記した際の 2^k (k \geq 0) の位の数は、X,Y を二進表記した際の 2^k の位の数のうち少なくとも片方が 1 であれば 1、そうでなければ 0 である。
制約
- 1\le N\le 4\times 10^5
- 0\le A_i < 2^{20}
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
N 行出力せよ。
i 行目 (1\le i\le N) には、 k=i の場合の答えを出力せよ。
入力例 1
4 1 2 3 5
出力例 1
1 2 6 5
- k=1 のとき: i=1 に対し A_i と A_k のビット単位 \mathrm{OR} 演算は 1 になります。したがって、 k=1 の場合の答えは A_1=1 です。
- k=2 のとき: i=1,2 に対し A_i と A_k のビット単位 \mathrm{OR} 演算はそれぞれ 3,2 になります。したがって、 k=2 の場合の答えは A_2=2 です。
- k=3 のとき: i=1,2,3 に対し A_i と A_k のビット単位 \mathrm{OR} 演算は全て 3 になります。したがって、 k=3 の場合の答えは A_1\times A_2\times A_3=6 です。
- k=4 のとき: i=1,2,3,4 に対し A_i と A_k のビット単位 \mathrm{OR} 演算はそれぞれ 5,7,7,5 になります。したがって、 k=4 の場合の答えは A_1\times A_4=5 です。
入力例 2
9 3 1 4 1 5 9 2 6 5
出力例 2
3 1 4 1 20 9 2 48 100
入力例 3
12 437926 528156 284664 1038330 692060 720863 602077 1027766 868190 532252 982711 876446
出力例 3
437926 528156 284664 94842632 158208162 985930968 548875758 875494466 345599613 605424119 111381243 768586512
Score : 700 points
Problem Statement
You are given a length-N sequence of non-negative integers A=(A_1,A_2,\ldots,A_N).
For k=1,2,\ldots,N, solve the following problem.
- Find the product, modulo 998244353, of A_i for all integers i between 1 and k, inclusive, such that the bitwise \mathrm{OR} operation of A_i and A_k equals A_k.
What is bitwise \mathrm{OR} operation?
The bitwise \mathrm{OR} of non-negative integers X and Y, denoted X\ \mathrm{OR}\ Y, is defined as follows.
- When X\ \mathrm{OR}\ Y is written in binary, the digit at the 2^k (k \geq 0) place is 1 if at least one of the digits at the 2^k place when X and Y are written in binary is 1, and 0 otherwise.
Constraints
- 1\le N\le 4\times 10^5
- 0\le A_i < 2^{20}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Output N lines.
The i-th line (1\le i\le N) should contain the answer for the case k=i.
Sample Input 1
4 1 2 3 5
Sample Output 1
1 2 6 5
- When k=1: For i=1, the bitwise \mathrm{OR} operation of A_i and A_k is 1. Therefore, the answer for the case k=1 is A_1=1.
- When k=2: For i=1,2, the bitwise \mathrm{OR} operation of A_i and A_k is 3,2, respectively. Therefore, the answer for the case k=2 is A_2=2.
- When k=3: For i=1,2,3, the bitwise \mathrm{OR} operation of A_i and A_k is all 3. Therefore, the answer for the case k=3 is A_1\times A_2\times A_3=6.
- When k=4: For i=1,2,3,4, the bitwise \mathrm{OR} operation of A_i and A_k is 5,7,7,5, respectively. Therefore, the answer for the case k=4 is A_1\times A_4=5.
Sample Input 2
9 3 1 4 1 5 9 2 6 5
Sample Output 2
3 1 4 1 20 9 2 48 100
Sample Input 3
12 437926 528156 284664 1038330 692060 720863 602077 1027766 868190 532252 982711 876446
Sample Output 3
437926 528156 284664 94842632 158208162 985930968 548875758 875494466 345599613 605424119 111381243 768586512