実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
この問題の問題設定は F 問題と一部共通しています。
2222 年の CatCoder では、CatCoder Double Contest(以下、C2C と略します)を開催することになりました。
いま、問題案を持っている writer が N 人います。 各 writer の問題案は難易度によって Hard, Medium, Easy の 3 種類に分類されており、i 人目の writer が持っている Hard, Medium, Easy の問題案の個数はそれぞれ A_i,B_i,C_i です。
各 C2C では Div.1, Div.2 の 2 部門を同時に 1 つずつ開催します。それぞれの部門の開催に必要な問題案は以下の通りです。
- Div.1:同じ writer の Hard, Medium の問題案を 1 つずつ
- Div.2:同じ writer の Medium, Easy の問題案を 1 つずつ
ここで、Div.1, Div.2 の writer は必ずしも同じである必要がない点に注意して下さい。 また、各問題案は高々 1 回の C2C の 1 つの部門にしか使用出来ません。
C2C を最大で何回開催出来るかを求めて下さい。
T 個のテストケースが与えられるので、それぞれについて答えを求めて下さい。
制約
- 1 \le T \le 10^5
- 1 \le N \le 2 \times 10^5
- 1 \le A_i,B_i,C_i \le 10^9
- 全てのテストケースにおける N の総和は 2 \times 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケースは以下の形式で与えられる。
N A_1 B_1 C_1 A_2 B_2 C_2 \vdots A_N B_N C_N
出力
T 行出力せよ。
i 行目には i 番目のテストケースについて、C2C を開催出来る回数としてありうる最大値を出力せよ。
入力例 1
5 2 3 1 4 1 5 3 1 1 1 1 3 5 7 5 1 11 99 3 1 2 5 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 6 835549144 866512240 105679868 473233032 625162103 823002638 125467290 37501686 380787083 8043910 721085797 254272563 97327826 744196952 18713225 978152989 90127986 33086297
出力例 1
2 0 7 2500000000 998830769
1 つ目のテストケースについて、以下のように問題案を使用することにより、C2C を 2 回開催出来ます。
| Div.1 | Div.2 | |
|---|---|---|
| 第 1 回 | 1 人目の writer の Hard, Medium | 2 人目の writer の Medium, Easy |
| 第 2 回 | 2 人目の writer の Hard, Medium | 2 人目の writer の Medium, Easy |
Score : 500 points
Problem Statement
The problem setting of this problem is partially shared with Problem F.
In the year 2222, CatCoder will hold the CatCoder Double Contest (abbreviated as C2C).
There are N writers who have problem proposals. Each writer's problem proposals are classified into 3 types by difficulty: Hard, Medium, Easy, and the i-th writer has A_i, B_i, C_i problem proposals of Hard, Medium, Easy, respectively.
Each C2C simultaneously holds 2 divisions, Div.1 and Div.2. The problem proposals required for each division are as follows:
- Div.1: One Hard and one Medium problem proposal from the same writer
- Div.2: One Medium and one Easy problem proposal from the same writer
Note that the writers for Div.1 and Div.2 do not necessarily have to be the same. Also, each problem proposal can be used in at most one division of one C2C.
Find the maximum number of times C2C can be held.
T test cases are given, so find the answer for each.
Constraints
- 1 \le T \le 10^5
- 1 \le N \le 2 \times 10^5
- 1 \le A_i,B_i,C_i \le 10^9
- The sum of N over all test cases is at most 2 \times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case is given in the following format:
N A_1 B_1 C_1 A_2 B_2 C_2 \vdots A_N B_N C_N
Output
Output T lines.
The i-th line should contain the maximum number of times C2C can be held for the i-th test case.
Sample Input 1
5 2 3 1 4 1 5 3 1 1 1 1 3 5 7 5 1 11 99 3 1 2 5 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 6 835549144 866512240 105679868 473233032 625162103 823002638 125467290 37501686 380787083 8043910 721085797 254272563 97327826 744196952 18713225 978152989 90127986 33086297
Sample Output 1
2 0 7 2500000000 998830769
For the first test case, C2C can be held 2 times by using problem proposals as follows:
| Div.1 | Div.2 | |
|---|---|---|
| 1st time | Hard, Medium from the 1st writer | Medium, Easy from the 2nd writer |
| 2nd time | Hard, Medium from the 2nd writer | Medium, Easy from the 2nd writer |
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
1,2,\dots,N の番号がついた N 個の品物があります。 品物 i の重みは 2^{X_i} で価値は Y_i です。
重みの和が W 以下になるように品物を 0 個以上選ぶとき、価値の和としてありうる最大値を求めて下さい。
T 個のテストケースが与えられるので、それぞれについて答えを求めて下さい。
制約
- 1 \le T \le 10^5
- 1 \le N \le 2 \times 10^5
- 1 \le W \le 10^{18}
- 0 \le X_i \lt 60
- 1 \le Y_i \le 10^9
- 全てのテストケースにおける N の総和は 2 \times 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケースは以下の形式で与えられる。
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
出力
T 行出力せよ。
i 行目には i 番目のテストケースについて、価値の和としてありうる最大値を出力せよ。
入力例 1
3 4 16 0 3 3 2 4 5 3 4 1 576460752303423487 59 1000000000 15 23752394551518 42 457687868 42 527769950 41 336200204 42 555090674 32 452384 42 697175056 38 62269946 39 24293218 40 214670437 37 6306990 39 103832403 41 205334902 37 20326312 35 4723060 42 176783630
出力例 1
7 0 3102936938
1 つ目のテストケースについて、各品物の重みと価値の組はそれぞれ (1,3),(8,2),(16,5),(8,4) です。
品物 1,4 を選ぶと、重みの和は 1+8=9 (\le 16)、価値の和は 3+4=7 となります。
2 つ目のテストケースについて、品物を選ぶ個数は 0 でも良い点に注意して下さい。
Score : 500 points
Problem Statement
There are N items numbered 1,2,\dots,N. Item i has weight 2^{X_i} and value Y_i.
When choosing 0 or more items such that the sum of weights is at most W, find the maximum possible sum of values.
T test cases are given, so find the answer for each.
Constraints
- 1 \le T \le 10^5
- 1 \le N \le 2 \times 10^5
- 1 \le W \le 10^{18}
- 0 \le X_i \lt 60
- 1 \le Y_i \le 10^9
- The sum of N over all test cases is at most 2 \times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case is given in the following format:
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
Output
Output T lines.
The i-th line should contain the maximum possible sum of values for the i-th test case.
Sample Input 1
3 4 16 0 3 3 2 4 5 3 4 1 576460752303423487 59 1000000000 15 23752394551518 42 457687868 42 527769950 41 336200204 42 555090674 32 452384 42 697175056 38 62269946 39 24293218 40 214670437 37 6306990 39 103832403 41 205334902 37 20326312 35 4723060 42 176783630
Sample Output 1
7 0 3102936938
For the first test case, the pairs of weight and value for items 1,2,3,4 are (1,3),(8,2),(16,5),(8,4), respectively.
If we choose items 1 and 4, the sum of weights is 1+8=9 (\le 16) and the sum of values is 3+4=7.
For the second test case, note that it is allowed to choose 0 items.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
どの文字も A または B であるような空でない文字列を AB 文字列と呼ぶことにします。
AB 文字列からなる集合 X が次を満たすとき、良い集合であるということにします。
- 長さ 10^{100} であるような AB 文字列は必ずある X の要素を接頭辞に持つ。
相異なる AB 文字列 S_1, S_2, \ldots, S_N が与えられます。各 k=1,2,\ldots,N について、集合 \lbrace S_1,S_2,\ldots,S_k\rbrace の部分集合であって良い集合であるものの個数を 998244353 で割った余りを求めて下さい。
制約
- 1\leq N\leq 2\times 10^5
- S_1, S_2, \ldots, S_N は相異なる AB 文字列
- \sum_{1\leq i\leq N}|S_i|\leq 5\times 10^5
入力
入力は以下の形式で標準入力から与えられる。
N S_1 S_2 \vdots S_N
出力
N 行出力して下さい。k 行目には、集合 \lbrace S_1,S_2,\ldots,S_k\rbrace の部分集合であって良い集合であるものの個数を 998244353 で割った余りを出力して下さい。
入力例 1
6 A B BA BB AA AB
出力例 1
0 1 2 5 10 25
- k=1 の場合:良い部分集合はありません。
- k=2 の場合:良い部分集合は \lbrace S_1,S_2\rbrace の 1 個です。
- k=3 の場合:良い部分集合は \lbrace S_1,S_2\rbrace, \lbrace S_1,S_2,S_3\rbrace の 2 個です。
- k=4 の場合:良い部分集合は \lbrace S_1,S_2\rbrace, \lbrace S_1,S_2,S_3\rbrace, \lbrace S_1,S_2,S_4\rbrace, \lbrace S_1,S_3,S_4\rbrace, \lbrace S_1,S_2,S_3,S_4\rbrace の 5 個です。
入力例 2
10 A B AABA AABB AB AA AAA BB AAB BA
出力例 2
0 1 2 4 8 20 41 82 170 425
Score : 600 points
Problem Statement
A non-empty string where every character is A or B is called an AB string.
A set X consisting of AB strings is called a good set when it satisfies the following:
- Every AB string of length 10^{100} has some element of X as a prefix.
You are given distinct AB strings S_1, S_2, \ldots, S_N. For each k=1,2,\ldots,N, find the number, modulo 998244353, of subsets of the set \lbrace S_1,S_2,\ldots,S_k\rbrace that are good sets.
Constraints
- 1\leq N\leq 2\times 10^5
- S_1, S_2, \ldots, S_N are distinct AB strings.
- \sum_{1\leq i\leq N}|S_i|\leq 5\times 10^5
Input
The input is given from Standard Input in the following format:
N S_1 S_2 \vdots S_N
Output
Output N lines. The k-th line should contain the number, modulo 998244353, of subsets of the set \lbrace S_1,S_2,\ldots,S_k\rbrace that are good sets.
Sample Input 1
6 A B BA BB AA AB
Sample Output 1
0 1 2 5 10 25
- For k=1: There are no good subsets.
- For k=2: There is 1 good subset: \lbrace S_1,S_2\rbrace.
- For k=3: There are 2 good subsets: \lbrace S_1,S_2\rbrace, \lbrace S_1,S_2,S_3\rbrace.
- For k=4: There are 5 good subsets: \lbrace S_1,S_2\rbrace, \lbrace S_1,S_2,S_3\rbrace, \lbrace S_1,S_2,S_4\rbrace, \lbrace S_1,S_3,S_4\rbrace, \lbrace S_1,S_2,S_3,S_4\rbrace.
Sample Input 2
10 A B AABA AABB AB AA AAA BB AAB BA
Sample Output 2
0 1 2 4 8 20 41 82 170 425
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
長さ N の非負整数列 A=(A_1,A_2,\dots ,A_N),B=(B_1,B_2,\dots ,B_N) と正整数 M が与えられます。
A の要素を自由に並び替えることが出来るとき、\max_{1\le i\le N} ((A_i+B_i) \bmod M) としてありうる最小値を求めて下さい。
T 個のテストケースが与えられるので、それぞれについて答えを求めて下さい。
制約
- 1 \le T \le 10^5
- 1 \le N \le 3 \times 10^5
- 1 \le M \le 10^9
- 0 \le A_i,B_i \lt M
- 全てのテストケースにおける N の総和は 3 \times 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケースは以下の形式で与えられる。
N M A_1 A_2 \ldots A_N B_1 B_2 \ldots B_N
出力
T 行出力せよ。
j 行目には j 番目のテストケースについて、\max_{1\le i\le N} ((A_i+B_i) \bmod M) としてありうる最小値を出力せよ。
入力例 1
3 3 6 3 1 4 2 0 1 1 1000000000 999999999 999999999 10 201 144 150 176 154 110 187 38 136 111 46 96 109 73 63 85 1 156 7 13 171
出力例 1
3 999999998 111
1 つ目のテストケースについて、A を 4,3,1 と並び替えると (A_i+B_i) \bmod M はそれぞれ 0,3,2 となり、これらの \max は 3 となります。
Score : 700 points
Problem Statement
You are given sequences of non-negative integers A=(A_1,A_2,\dots ,A_N),B=(B_1,B_2,\dots ,B_N) of length N and a positive integer M.
When the elements of A can be rearranged freely, find the minimum possible value of \max_{1\le i\le N} ((A_i+B_i) \bmod M).
T test cases are given, so find the answer for each.
Constraints
- 1 \le T \le 10^5
- 1 \le N \le 3 \times 10^5
- 1 \le M \le 10^9
- 0 \le A_i,B_i \lt M
- The sum of N over all test cases is at most 3 \times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case is given in the following format:
N M A_1 A_2 \ldots A_N B_1 B_2 \ldots B_N
Output
Output T lines.
The j-th line should contain the minimum possible value of \max_{1\le i\le N} ((A_i+B_i) \bmod M) for the j-th test case.
Sample Input 1
3 3 6 3 1 4 2 0 1 1 1000000000 999999999 999999999 10 201 144 150 176 154 110 187 38 136 111 46 96 109 73 63 85 1 156 7 13 171
Sample Output 1
3 999999998 111
For the first test case, if we rearrange A to 4,3,1, then (A_i+B_i) \bmod M becomes 0,3,2 respectively, and the \max of these is 3.
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 800 点
問題文
2 次元平面上に 1,2, \dots, N の番号がついた N 個の点があります。 点 i の座標は (i,Y_i) です。 なお、この問題では Y=(Y_1,Y_2,\dots ,Y_N) は (1,2, \dots ,N) の順列であることが保証されます。
\lbrace \texttt{点} 1,\texttt{点} 2,\dots ,\texttt{点} N \rbrace の要素数 2 以上の部分集合 S 全てに対するバウンディングボックスの面積の総和を 998244353 で割った余りを求めて下さい。
S に対するバウンディングボックスとは、 S に含まれる全ての点を内部または周上に含んでかつ x 軸に平行な辺を持つような長方形のうち、面積が最小であるものを指します。
制約
- 2 \le N \le 2 \times 10^5
- Y は (1,2, \dots ,N) の順列
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Y_1 Y_2 \ldots Y_N
出力
バウンディングボックスの面積の総和を 998244353 で割った余りを出力せよ。
入力例 1
4 2 3 1 4
出力例 1
50
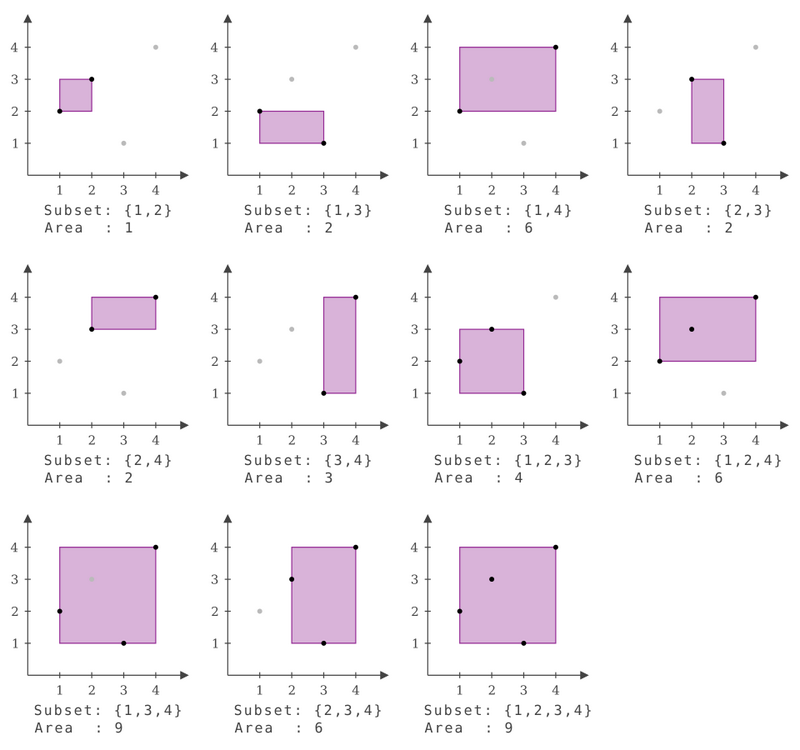
各部分集合とバウンディングボックスの面積は下図の通りです。面積の総和である 50 を出力します。
入力例 2
26 6 14 8 19 13 25 26 22 7 3 16 15 11 24 1 12 20 23 5 17 9 2 21 10 4 18
出力例 2
575187918
Score : 800 points
Problem Statement
There are N points numbered 1,2, \dots, N on the 2-dimensional plane. The coordinates of point i are (i,Y_i). In this problem, it is guaranteed that Y=(Y_1,Y_2,\dots ,Y_N) is a permutation of (1,2, \dots ,N).
Find the sum of the areas of bounding boxes for all subsets S of \lbrace \texttt{point}\,1,\texttt{point}\,2,\dots ,\texttt{point}\,N \rbrace with at least 2 elements, modulo 998244353.
The bounding box for S refers to the minimum area rectangle with sides parallel to the x-axis that contains all points in S inside or on the boundary.
Constraints
- 2 \le N \le 2 \times 10^5
- Y is a permutation of (1,2, \dots ,N).
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Y_1 Y_2 \ldots Y_N
Output
Output the sum, modulo 998244353, of the areas of bounding boxes.
Sample Input 1
4 2 3 1 4
Sample Output 1
50
Each subset and the area of its bounding box are shown in the figure below. Output the sum of areas, which is 50.

Sample Input 2
26 6 14 8 19 13 25 26 22 7 3 16 15 11 24 1 12 20 23 5 17 9 2 21 10 4 18
Sample Output 2
575187918
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1000 点
問題文
この問題の問題設定は A 問題と一部共通しています。
3333 年の CatCoder では、CatCoder Triple Contest(以下、C3C と略します)を開催することになりました。
いま、問題案を持っている writer が N 人います。 各 writer の問題案は難易度によって Hell, Hard, Medium, Easy, Baby の 5 種類に分類されており、i 人目の writer が持っている Hell, Hard, Medium, Easy, Baby の問題案の個数はそれぞれ A_i,B_i,C_i,D_i,E_i です。
各 C3C では Div.1, Div.2, Div.3 の 3 部門を同時に 1 つずつ開催します。それぞれの部門の開催に必要な問題案は以下の通りです。
- Div.1:同じ writer の Hell, Hard, Medium の問題案を 1 つずつ
- Div.2:同じ writer の Hard, Medium, Easy の問題案を 1 つずつ
- Div.3:同じ writer の Medium, Easy, Baby の問題案を 1 つずつ
ここで、Div.1, Div.2, Div.3 の writer は必ずしも同じである必要がない点に注意して下さい。 また、各問題案は高々 1 回の C3C の 1 つの部門にしか使用出来ません。
k=1,2,\dots,N について、1 人目から k 人目までの k 人の writer の問題案のみを使用することによって C3C を開催出来る回数の最大値を X_k とします。X_1,X_2,\dots ,X_N を求めて下さい。
T 個のテストケースが与えられるので、それぞれについて答えを求めて下さい。
制約
- 1 \le T \le 10^5
- 1 \le N \le 2 \times 10^5
- 1 \le A_i,B_i,C_i,D_i,E_i \le 10^9
- 全てのテストケースにおける N の総和は 2 \times 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケースは以下の形式で与えられる。
N A_1 B_1 C_1 D_1 E_1 A_2 B_2 C_2 D_2 E_2 \vdots A_N B_N C_N D_N E_N
出力
T 行出力せよ。
i 行目には i 番目のテストケースについて、X_1,X_2,\dots ,X_N を空白区切りで出力せよ。
入力例 1
3 2 3 3 3 3 3 3 1 4 2 5 7 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 10 145852338 455046273 447701888 302317605 187706517 469056787 117990013 461926296 216907828 419205454 89931495 63942616 324197994 555154220 469433755 285221794 487750820 398191999 232324766 44467392 356205020 422423283 451558541 314957395 11846473 212753197 384933474 328150388 111956686 11132031 414426705 377305504 500797865 354689082 115544977 176361367 59266253 439600074 328676554 233005233 310994713 74852265 430187235 889232556 487055975 22464564 297489263 186185204 29275688 641606972
出力例 1
1 2 333333333 666666666 1000000000 1333333333 1666666666 2000000000 2333333333 145852338 259612716 314817258 501663240 646419826 751331137 911803212 1016363776 1143191852 1169061978
1 つ目のテストケースについて、例えば k=2 のときは以下のように問題案を使用することにより C3C を 2 回開催出来ます。
| Div.1 | Div.2 | Div.3 | |
|---|---|---|---|
| 第 1 回 | 1 人目の writer の Hell, Hard, Medium | 1 人目の writer の Hard, Medium, Easy | 2 人目の writer の Medium, Easy, Baby |
| 第 2 回 | 2 人目の writer の Hell, Hard, Medium | 1 人目の writer の Hard, Medium, Easy | 2 人目の writer の Medium, Easy, Baby |
Score : 1000 points
Problem Statement
The problem setting of this problem is partially shared with Problem A.
In the year 3333, CatCoder will hold the CatCoder Triple Contest (abbreviated as C3C).
There are N writers who have problem proposals. Each writer's problem proposals are classified into 5 types by difficulty: Hell, Hard, Medium, Easy, Baby, and the i-th writer has A_i,B_i,C_i,D_i,E_i problem proposals of Hell, Hard, Medium, Easy, Baby, respectively.
Each C3C simultaneously holds 3 divisions, Div.1, Div.2, and Div.3. The problem proposals required for each division are as follows:
- Div.1: One Hell, one Hard, and one Medium problem proposal from the same writer
- Div.2: One Hard, one Medium, and one Easy problem proposal from the same writer
- Div.3: One Medium, one Easy, and one Baby problem proposal from the same writer
Note that the writers for Div.1, Div.2, and Div.3 do not necessarily have to be the same. Also, each problem proposal can be used in at most one division of one C3C.
For k=1,2,\dots,N, let X_k be the maximum number of times C3C can be held using only the problem proposals of the first k writers. Find X_1,X_2,\dots ,X_N.
T test cases are given, so find the answer for each.
Constraints
- 1 \le T \le 10^5
- 1 \le N \le 2 \times 10^5
- 1 \le A_i,B_i,C_i,D_i,E_i \le 10^9
- The sum of N over all test cases is at most 2 \times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case is given in the following format:
N A_1 B_1 C_1 D_1 E_1 A_2 B_2 C_2 D_2 E_2 \vdots A_N B_N C_N D_N E_N
Output
Output T lines.
The i-th line should contain X_1,X_2,\dots ,X_N separated by spaces for the i-th test case.
Sample Input 1
3 2 3 3 3 3 3 3 1 4 2 5 7 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 10 145852338 455046273 447701888 302317605 187706517 469056787 117990013 461926296 216907828 419205454 89931495 63942616 324197994 555154220 469433755 285221794 487750820 398191999 232324766 44467392 356205020 422423283 451558541 314957395 11846473 212753197 384933474 328150388 111956686 11132031 414426705 377305504 500797865 354689082 115544977 176361367 59266253 439600074 328676554 233005233 310994713 74852265 430187235 889232556 487055975 22464564 297489263 186185204 29275688 641606972
Sample Output 1
1 2 333333333 666666666 1000000000 1333333333 1666666666 2000000000 2333333333 145852338 259612716 314817258 501663240 646419826 751331137 911803212 1016363776 1143191852 1169061978
For the first test case, for example when k=2, C3C can be held 2 times by using problem proposals as follows:
| Div.1 | Div.2 | Div.3 | |
|---|---|---|---|
| 1st time | Hell, Hard, Medium from the 1st writer | Hard, Medium, Easy from the 1st writer | Medium, Easy, Baby from the 2nd writer |
| 2nd time | Hell, Hard, Medium from the 2nd writer | Hard, Medium, Easy from the 1st writer | Medium, Easy, Baby from the 2nd writer |