Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 200 点
問題文
N 個の整数 a_1,a_2,..,a_N が与えられます。えび君はこれらを書き換えて全て同じ整数にしようとしています。各a_i (1≦i≦N)は高々一回しか書き換えられません(書き換えなくても良い)。整数xを整数yに書き換えるとき、コストが(x-y)^2かかります。仮にa_i=a_j (i≠j)だとしても、ひとつ分のコストで同時に書き換えることは出来ません(入出力例2 を参照)。えび君が目的を達成するのに必要なコストの総和の最小値を求めてください。
制約
- 1≦N≦100
- -100≦a_i≦100
入力
入力は以下の形式で標準入力から与えられる。
N a_1 a_2 ... a_N
出力
えび君が全てを同じ整数に書き換えるのに必要なコストの総和の最小値を出力せよ。
入力例 1
2 4 8
出力例 1
8
全てを6に書き換えると、コストの総和は(4-6)^2+(8-6)^2=8となり、これが最小です。
入力例 2
3 1 1 3
出力例 2
3
全てを2に書き換えると(1-2)^2+(1-2)^2+(3-2)^2=3となります。各a_iごとに書き換えるので、二つの1を一度にコスト(1-2)^2で書き換えられるわけではないことに注意してください。
入力例 3
3 4 2 5
出力例 3
5
4は書き換えずに、2と5を共に4に書き換えることで(2-4)^2+(5-4)^2=5が達成できて、これが最小です。
入力例 4
4 -100 -100 -100 -100
出力例 4
0
何も書き換えなくともえび君は目的を達成しています。よってこの場合コストは0です。
Score : 200 points
Problem Statement
Evi has N integers a_1,a_2,..,a_N. His objective is to have N equal integers by transforming some of them.
He may transform each integer at most once. Transforming an integer x into another integer y costs him (x-y)^2 dollars. Even if a_i=a_j (i≠j), he has to pay the cost separately for transforming each of them (See Sample 2).
Find the minimum total cost to achieve his objective.
Constraints
- 1≦N≦100
- -100≦a_i≦100
Input
The input is given from Standard Input in the following format:
N a_1 a_2 ... a_N
Output
Print the minimum total cost to achieve Evi's objective.
Sample Input 1
2 4 8
Sample Output 1
8
Transforming the both into 6s will cost (4-6)^2+(8-6)^2=8 dollars, which is the minimum.
Sample Input 2
3 1 1 3
Sample Output 2
3
Transforming the all into 2s will cost (1-2)^2+(1-2)^2+(3-2)^2=3 dollars. Note that Evi has to pay (1-2)^2 dollar separately for transforming each of the two 1s.
Sample Input 3
3 4 2 5
Sample Output 3
5
Leaving the 4 as it is and transforming the 2 and the 5 into 4s will achieve the total cost of (2-4)^2+(5-4)^2=5 dollars, which is the minimum.
Sample Input 4
4 -100 -100 -100 -100
Sample Output 4
0
Without transforming anything, Evi's objective is already achieved. Thus, the necessary cost is 0.
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 400 点
問題文
文字列 t について、t の長さが 2 以上であり、かつ t の中の文字のうち過半数が同じ文字であるとき、t をアンバランスであると呼ぶことにします。例えば、voodoo や melee はアンバランスであり、noon や a はアンバランスではありません。
小文字のアルファベットからなる文字列 s が与えられます。s にアンバランスな (連続する) 部分文字列が存在するか判定してください。存在する場合は、s の中でそのような部分文字列が存在する位置を一つ示してください。
制約
- 2 ≦ |s| ≦ 10^5
- s は小文字のアルファベットのみからなる。
部分点
- 2 ≦ |s| ≦ 100 を満たすデータセットに正解した場合は、200 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
s
出力
s にアンバランスな部分文字列が存在しない場合は、-1 -1 と出力せよ。
s にアンバランスな部分文字列が存在する場合は、そのような部分文字列の一つを s_a s_{a+1} ... s_{b} (1 ≦ a < b ≦ |s|) として、a b と出力せよ。そのような部分文字列が複数存在する場合は、いずれも正解とみなされる。
入力例 1
needed
出力例 1
2 5
文字列 s_2 s_3 s_4 s_5 = eede はアンバランスな文字列です。他にもアンバランスな部分文字列は存在し、例えば 2 6 と出力しても正解となります。
入力例 2
atcoder
出力例 2
-1 -1
文字列 atcoder はアンバランスな部分文字列を持ちません。
Score : 400 points
Problem Statement
Given a string t, we will call it unbalanced if and only if the length of t is at least 2, and more than half of the letters in t are the same. For example, both voodoo and melee are unbalanced, while neither noon nor a is.
You are given a string s consisting of lowercase letters. Determine if there exists a (contiguous) substring of s that is unbalanced. If the answer is positive, show a position where such a substring occurs in s.
Constraints
- 2 ≦ |s| ≦ 10^5
- s consists of lowercase letters.
Partial Score
- 200 points will be awarded for passing the test set satisfying 2 ≦ N ≦ 100.
Input
The input is given from Standard Input in the following format:
s
Output
If there exists no unbalanced substring of s, print -1 -1.
If there exists an unbalanced substring of s, let one such substring be s_a s_{a+1} ... s_{b} (1 ≦ a < b ≦ |s|), and print a b. If there exists more than one such substring, any of them will be accepted.
Sample Input 1
needed
Sample Output 1
2 5
The string s_2 s_3 s_4 s_5 = eede is unbalanced. There are also other unbalanced substrings. For example, the output 2 6 will also be accepted.
Sample Input 2
atcoder
Sample Output 2
-1 -1
The string atcoder contains no unbalanced substring.
Time Limit: 4 sec / Memory Limit: 256 MB
配点 : 800 点
問題文
競プロ幼稚園には1～Nの番号がついたN人の子供がいます。えび先生は、区別できないC個のキャンディーを子供たちに分配することにしました。子供iのはしゃぎ度がx_iの時、キャンディーをa個もらうと子供iのうれしさはx_i^aになります。幼稚園の活発度はN人の子供たちのうれしさの積になります。各子供にキャンディーを非負整数個配ってC個配りきる方法それぞれに対して幼稚園の活発度を計算して、その総和を子供たちのはしゃぎ度x_1,..,x_Nの関数とみてf(x_1,..,x_N)とおきます。A_i,B_i (1≦i≦N)が与えられるので、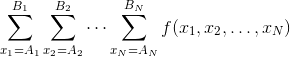 
を10^9+7で割ったあまりを求めてください。
制約
- 1≦N≦400
- 1≦C≦400
- 1≦A_i≦B_i≦400 (1≦i≦N)
部分点
- A_i=B_i (1≦i≦N) を満たすデータセットに正解した場合は、部分点として400 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N C A_1 A_2 ... A_N B_1 B_2 ... B_N
出力
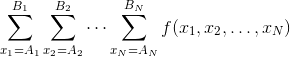の値を10^9+7で割ったあまりを出力せよ。
入力例 1
2 3 1 1 1 1
出力例 1
4
A_i=B_iなので部分点の条件を満たします。 子供1,2のはしゃぎ度が共に1のもの(f(1,1))を考えればよく、この時、
- 子供1に0個,子供2に3個のキャンディーをあげると、幼稚園の活発度は1^0*1^3=1
- 子供1に1個,子供2に2個のキャンディーをあげると、幼稚園の活発度は1^1*1^2=1
- 子供1に2個,子供2に1個のキャンディーをあげると、幼稚園の活発度は1^2*1^1=1
- 子供1に3個,子供2に0個のキャンディーをあげると、幼稚園の活発度は1^3*1^0=1
従ってf(1,1)=1+1+1+1=4となり、fを足し合わせた答えは4です。
入力例 2
1 2 1 3
出力例 2
14
子供が一人なので、子供1のうれしさが幼稚園の活発度になります。また、キャンディの配り方は2つとも子供1にあげる1通りしかないため、この時の幼稚園の活発度はfの値に等しくなります。
- 子供1のはしゃぎ度が1の時、f(1)=1^2=1
- 子供1のはしゃぎ度が2の時、f(2)=2^2=4
- 子供1のはしゃぎ度が3の時、f(3)=3^2=9
従って答えは1+4+9=14となります。
入力例 3
2 3 1 1 2 2
出力例 3
66
f(1,1)=4 , f(1,2)=15 , f(2,1)=15 , f(2,2)=32 となることがわかるので、答えは4+15+15+32=66になります。
入力例 4
4 8 3 1 4 1 3 1 4 1
出力例 4
421749
部分点の条件を満たします。
入力例 5
3 100 7 6 5 9 9 9
出力例 5
139123417
Score : 800 points
Problem Statement
12:17 (UTC): The sample input 1 and 2 were swapped. The error is now fixed. We are very sorry for your inconvenience.
There are N children in AtCoder Kindergarten, conveniently numbered 1 through N. Mr. Evi will distribute C indistinguishable candies to the children.
If child i is given a candies, the child's happiness will become x_i^a, where x_i is the child's excitement level. The activity level of the kindergarten is the product of the happiness of all the N children.
For each possible way to distribute C candies to the children by giving zero or more candies to each child, calculate the activity level of the kindergarten. Then, calculate the sum over all possible way to distribute C candies. This sum can be seen as a function of the children's excitement levels x_1,..,x_N, thus we call it f(x_1,..,x_N).
You are given integers A_i,B_i (1≦i≦N). Find 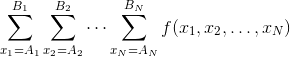modulo 10^9+7.
Constraints
- 1≦N≦400
- 1≦C≦400
- 1≦A_i≦B_i≦400 (1≦i≦N)
Partial Score
- 400 points will be awarded for passing the test set satisfying A_i=B_i (1≦i≦N).
Input
The input is given from Standard Input in the following format:
N C A_1 A_2 ... A_N B_1 B_2 ... B_N
Output
Print the value of 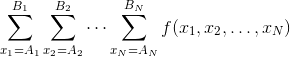modulo 10^9+7.
Sample Input 1
2 3 1 1 1 1
Sample Output 1
4
This case is included in the test set for the partial score, since A_i=B_i. We only have to consider the sum of the activity level of the kindergarten where the excitement level of both child 1 and child 2 are 1 (f(1,1)).
- If child 1 is given 0 candy, and child 2 is given 3 candies, the activity level of the kindergarten is 1^0*1^3=1.
- If child 1 is given 1 candy, and child 2 is given 2 candies, the activity level of the kindergarten is 1^1*1^2=1.
- If child 1 is given 2 candies, and child 2 is given 1 candy, the activity level of the kindergarten is 1^2*1^1=1.
- If child 1 is given 3 candies, and child 2 is given 0 candy, the activity level of the kindergarten is 1^3*1^0=1.
Thus, f(1,1)=1+1+1+1=4, and the sum over all f is also 4.
Sample Input 2
1 2 1 3
Sample Output 2
14
Since there is only one child, child 1's happiness itself will be the activity level of the kindergarten. Since the only possible way to distribute 2 candies is to give both candies to child 1, the activity level in this case will become the value of f.
- When the excitement level of child 1 is 1, f(1)=1^2=1.
- When the excitement level of child 1 is 2, f(2)=2^2=4.
- When the excitement level of child 1 is 3, f(3)=3^2=9.
Thus, the answer is 1+4+9=14.
Sample Input 3
2 3 1 1 2 2
Sample Output 3
66
Since it can be seen that f(1,1)=4 , f(1,2)=15 , f(2,1)=15 , f(2,2)=32, the answer is 4+15+15+32=66.
Sample Input 4
4 8 3 1 4 1 3 1 4 1
Sample Output 4
421749
This case is included in the test set for the partial score.
Sample Input 5
3 100 7 6 5 9 9 9
Sample Output 5
139123417
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 800 点
問題文
しぐはキーボードを製作しました。シンプルさを極限まで追求したこのキーボードには、0 キー、1 キー、バックスペースキーの 3 つしかキーがありません。
手始めに、しぐはこのキーボードで簡単なテキストエディタを操作してみることにしました。このエディタには常に一つの文字列が表示されます（文字列が空のこともあります）。エディタを起動した直後では、文字列は空です。キーボードの各キーを押すと、文字列が次のように変化します。
0キー: 文字列の右端に文字0が挿入される。1キー: 文字列の右端に文字1が挿入される。- バックスペースキー: 文字列が空なら、何も起こらない。そうでなければ、文字列の右端の 1 文字が削除される。
しぐはエディタを起動し、これらのキーを合計で N 回押しました。その結果、いまエディタに文字列 s が表示されています。このようなキーの押し方の個数を 10^9 + 7 で割った余りを求めてください。
制約
- 1 ≦ N ≦ 5000
- 1 ≦ |s| ≦ N
- s は文字
0,1のみからなる。
部分点
- 1 ≦ N ≦ 300 を満たすデータセットに正解すると、400 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N s
出力
最終的にエディタに文字列 s が表示されるような N 回のキーの押し方の個数を 10^9+7 で割った余りを出力せよ。
入力例 1
3 0
出力例 1
5
バックスペースキーを B と表記すると、次の 5 通りの押し方で最終的に表示される文字列が 0 となります: 00B, 01B, 0B0, 1B0, BB0。最後の押し方では、バックスペースキーを押すときに何も起こりません。
入力例 2
300 1100100
出力例 2
519054663
入力例 3
5000 01000001011101000100001101101111011001000110010101110010000
出力例 3
500886057
Score : 800 points
Problem Statement
Sig has built his own keyboard. Designed for ultimate simplicity, this keyboard only has 3 keys on it: the 0 key, the 1 key and the backspace key.
To begin with, he is using a plain text editor with this keyboard. This editor always displays one string (possibly empty). Just after the editor is launched, this string is empty. When each key on the keyboard is pressed, the following changes occur to the string:
- The
0key: a letter0will be inserted to the right of the string. - The
1key: a letter1will be inserted to the right of the string. - The backspace key: if the string is empty, nothing happens. Otherwise, the rightmost letter of the string is deleted.
Sig has launched the editor, and pressed these keys N times in total. As a result, the editor displays a string s. Find the number of such ways to press the keys, modulo 10^9 + 7.
Constraints
- 1 ≦ N ≦ 5000
- 1 ≦ |s| ≦ N
- s consists of the letters
0and1.
Partial Score
- 400 points will be awarded for passing the test set satisfying 1 ≦ N ≦ 300.
Input
The input is given from Standard Input in the following format:
N s
Output
Print the number of the ways to press the keys N times in total such that the editor displays the string s in the end, modulo 10^9+7.
Sample Input 1
3 0
Sample Output 1
5
We will denote the backspace key by B. The following 5 ways to press the keys will cause the editor to display the string 0 in the end: 00B, 01B, 0B0, 1B0, BB0. In the last way, nothing will happen when the backspace key is pressed.
Sample Input 2
300 1100100
Sample Output 2
519054663
Sample Input 3
5000 01000001011101000100001101101111011001000110010101110010000
Sample Output 3
500886057