Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
年商 10 億円を達成したAtCoder社のオフィスビルは、地上 10^9 階地下 10^9 階の超高層ビルです。
ロビーは 1 階にあり、その上には 2,3,4,...,10^9 階、その下には地下 1,2,...,10^9 階というように階が続きます。
あいにくすべてのエレベーターが壊れてしまったので、高橋君は A 階からそれより上にある B 階まで階段で上がることにしました。
AtCoder社のオフィスビルにはすべての上下に隣り合う階の間に階段があります。また、高橋君は階段を下ることはしません。
高橋君は階段を何階分上る必要があるでしょうか。ただし、x > 0 に対し、-x 階は地下 x 階のことを表すこととします。
入力
入力は以下の形式で標準入力から与えられる。
A B
- 1 行目には、整数 A,B(-10^9 ≦ A < B ≦ 10^9, A ≠ 0, B ≠ 0) が空白を区切りとして与えられる。
出力
高橋君が何階分の階段を上る必要があるかを表す整数 1 つを出力せよ。
出力の最後には改行を忘れないこと。
入力例1
3 6
出力例1
3
3 階から 4 階、4 階から 5 階、5 階から 6 階に上がる階段を上る必要があります。
入力例2
-1 1
出力例2
1
地下 1 階の上の階は地上 1 階です。
入力例3
-7 -2
出力例3
5
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
AtCoderじゃんけんの大会が開かれています。AtCoderじゃんけんとは、2 人で行う以下のようなゲームです。
- まず、2 人がそれぞれ独立にグー、チョキ、パーのいずれかの手を出す。
- 2 人のAtCoderのレーティングが等しくなければ、レーティングが高いほうを勝者とする。
- 2 人のAtCoderのレーティングが等しく、2 人の出した手が異なるならば、通常のじゃんけんの勝者を勝者とする。
- 2 人のAtCoderのレーティングが等しく、2 人の出した手も等しいならば、引き分けとする。
大会には N 人の参加者がおり、大会期間中同じ参加者は同じ手を出し続け、また大会期間中にレーティングが変化することはありません。
大会では、すべての参加者が、ほかの N-1 人の参加者とちょうど 1 回ずつAtCoderじゃんけんをします。
それぞれの人のレーティングと出す手が与えられるので、すべての参加者について、大会終了時の対戦成績が何勝何敗何引き分けかを答えてください。
ただし、通常のじゃんけんにおいては、グーはチョキに、チョキはパーに、パーはグーに、それぞれ勝つものとします。
入力
入力は以下の形式で標準入力から与えられる。
N R_1 H_1 . . . R_N H_N
- 1 行目には、整数 N(1 ≦ N ≦ 100000) が与えられる。
- 続く N 行には、 i 番目の参加者の情報を表す整数 R_i, H_i(1 ≦ R_i ≦ 100000, 1 ≦ H_i ≦ 3) が空白を区切りとして与えられる。これは、i 番目の参加者のレーティングが R_i で、出す手が H_i=1 のときグー、H_i=2 のときチョキ、H_i=3 のときパーであることを表す。
出力
- 出力は N 行からなる。
- i 行目には、i 番目の参加者の勝ち数、負け数、引き分け数を表す整数 3 つを順に空白区切りで出力せよ。
出力の最後には改行を忘れないこと。
入力例1
6 2 1 2 2 3 2 5 3 2 2 3 3
出力例1
2 3 0 0 4 1 4 1 0 5 0 0 0 4 1 3 2 0
勝敗表は図のようになります。
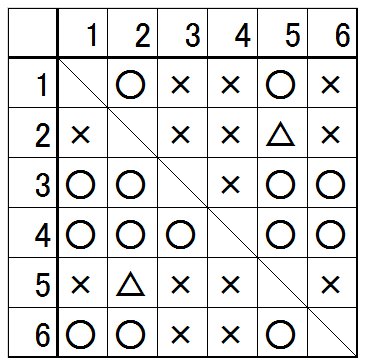
図 1 : 勝敗表
入力例2
2 1999 3 2000 1
出力例2
0 1 0 1 0 0
慈悲はありません。
入力例3
8 3200 2 2800 3 2800 2 2700 1 2800 2 3200 1 2700 1 3200 3
出力例3
6 1 0 2 5 0 3 3 1 0 6 1 3 3 1 6 1 0 0 6 1 6 1 0
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君には足が N 本あり、i 番目の足は L_i 本の骨が一列につながった構造をしています。 すべての足の片方の端は、高橋君の胴体につながっています。高橋君の胴体には骨はありません。
今回高橋君は、自分のすべての足のすべての骨に 0 または 1 の文字を書き込むことにしました。
高橋君は文字の書き込み方に強いこだわりを持っており、任意の異なる 2 本の足 A,B について、 A の胴体につながっていないほうの端から B の胴体につながっていないほうの端までの胴体を経由する経路上にある骨に書かれた文字をすべて順に読むと回文になっているとき、またその時のみ満足します。
高橋君が満足する文字の書き込み方の数を 10^9+7 で割った余りを求めてください。
入力
入力は以下の形式で標準入力から与えられる。
N L_1 . . . L_N
- 1 行目には、高橋君の足の本数を表す整数 N(1 ≦ N ≦ 100000) が与えられる。
- 続く N 行には、i 番目の足の長さを表す整数 L_i(1 ≦ L_i ≦ 10^9) が与えられる。
出力
高橋君が満足する文字の書き込み方の数を 10^9+7 で割った余りを表す整数 1 つを出力せよ。
出力の最後には改行を忘れないこと。
入力例1
3 2 4 8
出力例1
8
3 本の足に書く文字列を胴体に接続していないほうから読むと、例えば (01,0111,01111111) などが条件を満たします。
入力例2
8 2 1 4 3 6 5 8 7
出力例2
4
入力例3
5 700000000 20000000 9000000 600000000 30000000
出力例3
861838989
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
AtCoder市には 1 から N までの番号のついた N 個の町があり、それらは N-1 本の双方向に通行可能な距離 1 の道路によって結ばれています。 どの町からどの町へも、いくつかの道を経由してたどり着くことが出来ます。
AtCoder市には高橋君が Q 人おり、i 人目の高橋君は町 s_i から町 t_i に行きたいです。
AtCoder市のいくつかの町にはたこ焼き屋があります。高橋君たちはみな、2 秒間に距離 1 進む速度で歩きますが、たこ焼き屋のある町でたこ焼きを食べたあとは歩く速度が 1 秒間に距離 1 進む速度になります。 また高橋君たちはみな小食なので、たこ焼きを複数回食べることはしません。もちろん、たこ焼き屋のある町をたこ焼きを食べずに通過することは可能です。 また、たこ焼きを食べずに町 t_i に到着してもかまいません。
AtCoder市の町の接続関係が与えられるので、 Q 人の高橋君すべてに対し、最適に行動したときの町 s_i から町 t_iへの移動に費やされる時間の最小値を求めてください。 高橋君たちはみなたこ焼きのプロなので、たこ焼きを食べるのにかかる時間は無視できるものとします。
入力
入力は以下の形式で標準入力から与えられる。
N Q
A_1 B_1
.
.
.
A_{N-1} B_{N-1}
S
s_1 t_1
.
.
.
s_Q t_Q
- 1 行目には、整数 N(1 ≦ N ≦ 100000) と Q(1 ≦ Q ≦ 100000) が空白を区切りとして与えられる。
- 続く N-1 行には、 i 番目の道の情報を表す整数 A_i, B_i(1 ≦ A_i ≦ N, 1 ≦ B_i ≦ N, A_i ≠ B_i) が空白を区切りとして与えられる。これは、町 A_i と町 B_i を結ぶ道があることを表す。
- 続く行には、0 と 1 のみからなる長さ N の文字列が与えられる。この i 文字目が 0 のとき町 i にはたこ焼き屋がないことを、1 のとき町 i にはたこ焼き屋があることを表す。
- 続く Q 行には、i 人目の高橋君の移動の始点と目的地を表す整数 s_i,t_i(1 ≦ s_i ≦ N, 1 ≦ t_i ≦ N) が与えられる。
出力
出力は Q 行からなる。
i 行目には、i 人目の高橋君が最適に行動したときの移動にかかる時間の最小値を 1 行に出力せよ。
出力の最後には改行を忘れないこと。
入力例1
7 4 1 2 2 3 2 4 4 5 5 6 6 7 0010000 1 5 1 7 6 1 3 3
出力例1
6 9 8 0
最初のクエリでは、町 1,2,4,5 を順に訪れる場合が最善となります。 2 番目のクエリでは、町 1,2,3,2,4,5,6,7 と順に訪れ、途中町 3 のたこ焼き屋に寄る場合が最善となります。
入力例2
5 2 3 2 2 4 1 4 2 5 00000 1 5 2 3
出力例2
6 2
入力例3
12 10 1 2 2 3 2 4 10 12 1 5 3 11 5 6 9 10 5 7 3 9 8 7 000100100010 1 2 1 4 8 3 6 12 12 8 8 12 6 8 8 6 1 12 5 12
出力例3
2 4 6 11 14 9 5 4 9 9