Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君は素数判定アルゴリズムが大好きです。毎日さまざまな素数判定アルゴリズムを実装して遊んでいます。 しかし、高橋君は素数判定をしすぎてしまったので、素数判定に飽きてしまいました。 そこで高橋君は、「素数っぽく見える数」判定をすることにしました。
1以上の整数Nは、以下のように「素数っぽい」かどうかが判定されます。
- Nが素数であるなら、Nは「素数っぽい」
- Nが合成数であるなら、Nを10進表記した時の1の位が偶数でも5でもなく、各桁の和が3で割り切れないならば、Nは「素数っぽい」
- それ以外の場合、Nは「素数っぽくない」
整数Nが与えられるので、Nが「素数っぽい」場合は"Prime"、そうでない場合は"Not Prime"と出力してください。
入力
入力は以下の形式で標準入力から与えられる。
N
- 1 行目には、整数N(1 ≦ N ≦ 10^9)が与えられる。
出力
Nが「素数っぽい」場合は"Prime"、そうでない場合は"Not Prime"と出力せよ。
出力の末尾に改行を入れること。(21:40修正)入力例1
42
出力例1
Not Prime
42は合成数かつ1の位が偶数なので、「素数っぽくない」と判定されます。
入力例2
49
出力例2
Prime
49は素数ではありませんが、「素数っぽい」と判定されます。
入力例3
3
出力例3
Prime
3は素数なので、「素数っぽい」と判定されます。
入力例4
1
出力例4
Not Prime
1は素数でも合成数でもないので、「素数っぽくない」と判定されます。
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君は最短路アルゴリズムが大好きです。毎日さまざまな最短路アルゴリズムを実装して遊んでいます。 しかし、高橋君は最短路を求めすぎてしまったので、最短路を求めるのに飽きてしまいました。
そこで高橋君は、ある頂点からほかの頂点への最短距離が特定の値になるような頂点数がNですべての辺の長さが1の無向単純グラフの数を数えることにしました。
より正確には、高橋君は同じ頂点の間を結ぶ辺が複数存在せず、またすべての辺の2端点の頂点が異なるグラフの頂点を順に1,2,...,Nとして、 任意のiに対し、頂点1と頂点iを結ぶ経路上に存在する辺の個数の最小値がA_iになるようなグラフの総数を数えます。
整数NとA_1,...,A_Nが与えられるので、このようなグラフの個数を10^9+7で割った余りを求めてください。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 ... A_N
- 1 行目には、グラフの頂点数N(1 ≦ N ≦ 10^5)が与えられる。
- 2 行目には、頂点1から頂点iまでの最短距離を表す整数列A_1,...,A_N(0 ≦ A_1,...,A_N ≦ N-1)が空白区切りで与えられる。
出力
条件を満たすグラフの個数を10^9+7で割った余りを出力せよ。
出力の末尾に改行を入れること。(21:40修正)入力例1
4 0 1 1 2
出力例1
6
下図の6通りのグラフが条件を満たします。
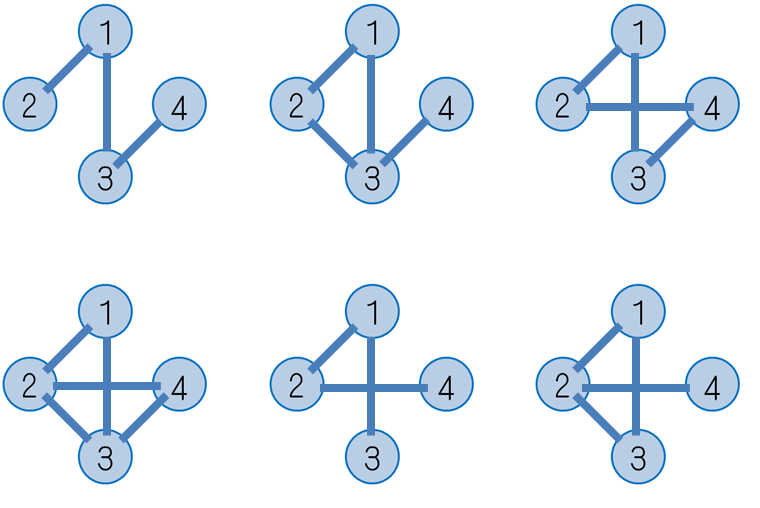
入力例2
4 0 1 2 0
出力例2
0
すべての辺の長さは1なので、頂点1,4間の距離が0となるグラフはありません。
入力例3
3 1 1 2
出力例3
0
頂点1から頂点1までの距離は1にはなりえません。
入力例4
17 0 1 1 2 2 4 3 2 4 5 3 3 2 1 5 4 2
出力例4
855391686
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君は、H × Wのグリッドの上に住んでいます。左下のマスは(1,1)で、右上のマスは(W,H)です。 しかし、このグリッドは少々厄介で、たまにビームが飛んできます。 人間である高橋君はビームに当たると「たいへんなこと」になってしまうので、できればビームには当たりたくありません。
ビームは、(時刻、方向、座標)の組で与えられます。時刻とは、そのビームが飛んでくる時刻、方向とは、縦または横です。
具体的には、ビーム(t,縦,a)は、時刻tに、1 ≦ i ≦ Hを満たすすべてのiに対してマス(a,i)を、 ビーム(t,横,a)は、時刻tに、1 ≦ i ≦ Wを満たすすべてのiに対してマス(i,a)を通過します。それ以外のマスは通過しません。
幸い高橋君は、いつ、どのようなビームが飛んでくるかの情報をすべて持っています。そのため、すべてのビームを、最短の移動回数でよけようと思っています。 高橋君は、辺を介して隣り合うマスに、1回で移動することができます。
高橋君は日頃からトレーニングに勤しんでいるので、単位時間に任意の回数移動することができます。 また、高橋君は、初期位置を自由に選ぶことができ、最後にどのマスにいてもよいこととします。なお、高橋君はグリッドの外に出ることはできません。
高橋君の移動回数の最小値を求めてください。もし高橋君がビームに当たらずに移動することが不可能ならば、かわりに-1を出力してください。
入力
入力は以下の形式で標準入力から与えられる。
W H Q T_1 D_1 X_1 . . . T_Q D_Q X_Q
- 1 行目には、整数W,H,Q(1 ≦ W,H ≦ 10^5, 0 ≦ Q ≦10^5)が与えられる。これらはそれぞれ、グリッドの横の長さ、縦の長さ、ビームが飛んでくる回数を表す。
- 2 行目からQ+1行目には、ビームの情報が与えられる。このうちi行目には、T_i,D_i,X_i(1 ≦ T_i ≦10^5, 0 ≦ D_i ≦ 1, D_i=0のとき1 ≦ X_i ≦ W, D_i=1のとき1 ≦ X_i ≦ H)が与えられる。D_i=0のときビーム(T_i,縦,X_i)が、D_i=1のときビーム(T_i,横,X_i)が飛んでくることを表す。また、任意のi,jに対し、(T_i,D_i,X_i) ≠ (T_j,D_j,X_j)を満たす。
部分点
この問題には部分点が設定されている。
- 1 ≦ W,H,Q ≦ 100, T_i ≦ 100(1 ≦ i ≦ Q) を満たすデータセットに正解した場合は 30 点が与えられる。
出力
ビームに一度も当たらないような移動が可能な場合、高橋君の移動回数の最小値を出力せよ。そうでない場合、-1を出力せよ。
出力の末尾に改行を入れること。(21:40修正)入力例1
3 2 8 1 0 2 3 0 2 4 1 2 2 1 2 4 0 3 2 0 3 1 1 1 2 0 1
出力例1
3
高橋君は以下の動きで、すべてのビームをよけることができます。
- はじめ、高橋君は(3,2)にいる
- 時刻1.5に、(2,2)に移動し、さらに(2,1)に移動する
- 時刻2.5に、(1,1)に移動する
入力例2
2 4 10 3 1 1 2 1 3 3 0 1 2 1 4 1 1 3 2 1 2 3 1 2 1 0 1 3 1 4 2 0 2
出力例2
4
入力例3
3 3 5 1 0 3 1 0 2 1 1 3 1 1 2 1 0 1
出力例3
-1
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君はsuffix arrayの構築アルゴリズムが大好きです。毎日さまざまなsuffix arrayの構築アルゴリズムを実装して遊んでいます。 しかし、高橋君はsuffix arrayを構築しすぎてしまったので、suffix arrayを構築するのに飽きてしまいました。 そこで高橋君は、与えられた順列に対し、その順列をsuffix arrayに持つような辞書順最小の文字列を求めることにしました。
ただし、2つの文字列X_1,X_2,...,X_sとY_1,Y_2,...,Y_tに対し、辞書順でX<Yとは、以下のいずれか片方の条件を満たすこととします。
- ある整数i(1 ≦ i ≦ min(s,t))が存在し、1 ≦ j ≦ i-1を満たす任意の整数jに対してX_j=Y_jで、かつX_i<Y_i
- 任意の整数i(1 ≦ i ≦ min(s,t))に対してX_i=Y_iで、かつs<t
また、与えられた文字列Sに対し、そのsuffix arrayとは、すべてのiに対して、Sのi文字目から末尾までを順に並べた文字列を列挙し、その文字列たちを辞書順に並び替えた列の各要素に対し、対応するiを順に並べたものです。 たとえば、文字列ABACABAのsuffix arrayは[7,5,1,3,6,2,4]となります。
長さNの順列が与えられるので、その順列をsuffix arrayに持つ英大文字のみからなる辞書順最小の文字列を求めてください。そのような文字列が存在しなければ、代わりに-1を出力してください。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 ... A_N
- 1 行目には、整数N(1 ≦ N ≦ 10^6)が与えられる。
- 2 行目には、整数列A_1,...,A_N(1 ≦ A_1,...,A_N ≦ N)が与えられる。これらN個の整数はどの2つも互いに異なることが保障される。
出力
順列A_1,...,A_Nをsuffix arrayに持つ辞書順最小の文字列を出力せよ。
出力の末尾に改行を入れること。(21:40修正)入力例1
7 7 5 1 3 6 2 4
出力例1
ABACABA
条件を満たす文字列は他にもCXHZBWAなどがありますが、辞書順最小のABACABAを出力します。
入力例2
12 7 1 9 10 2 4 3 6 12 5 11 8
出力例2
BDEDGFAHCCGG