Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君には「未来視」という能力がある。彼は大学で N 個の科目を履修しており、全ての科目の試験で 80 点以上を取ることが目標である。たった今見た「未来視」によると、各科目 i について、勉強せずにその科目の試験を受けると m_i 点を取ることが予測される。高橋君は 1 つの科目を 1 分間勉強するごとに、その科目の試験で取ることが予測される点数を 1 点上げることができる。「未来視」が正しいとして、高橋君が目標を達成するために必要な最短の合計勉強時間を求めよ。
入力
入力は以下の形式で標準入力から与えられる。
N m_1 m_2 .. m_N
- 1 行目には、高橋君が履修している科目の数 N (1 ≦ N ≦ 25) が与えられる。
- 2 行目には、各科目 i (1 ≦ i ≦ N) について、勉強せずにその科目の試験を受けたときに取ることが予測される得点 m_i (0 ≦ m_i ≦ 100) がスペース区切りで与えられる。
出力
標準出力に、高橋君が目標を達成するために必要な最短の合計勉強時間 (分単位) を出力し、末尾で改行せよ。
入力例1
5 70 90 60 80 50
出力例1
60
科目 1 の勉強を 10 分間、科目 3 の勉強を 20 分間、科目 5 の勉強を 30 分間すればよい。
入力例2
6 100 100 100 100 100 100
出力例2
0
何もしなくてよい。
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
バウムテストとは、被験者に「木」の絵を描かせることで被験者の心理状態を読み取る心理検査である。この検査を受けた高橋君は、 N 個の頂点と M 本の辺からなる無向グラフを描いた。このグラフの連結成分のうち木であるようなもの、すなわち閉路を持たないものの個数を求めよ。
入力
入力は以下の形式で標準入力から与えられる。
N M u_1 v_1 u_2 v_2 : u_M v_M
- 1 行目には、高橋君が描いた無向グラフに含まれる頂点の数 N (2 ≦ N ≦ 100) と辺の数 M (1 ≦ M ≦ N×(N-1)/2) がスペース区切りで与えられる。頂点には 1 から N の番号が振られている。
- 2 行目から M+1 行目は各辺の情報を含む。 i+1 行目 (1 ≦ i ≦ M) には、辺 i が結ぶ 2 頂点の番号 u_i, v_i (1 ≦ u_i < v_i ≦ N) がスペース区切りで与えられる。どの 2 頂点についても、それらを直接結ぶ辺は高々 1 本しか存在しない。
出力
標準出力に、高橋君が描いた無向グラフの連結成分のうち木であるものの個数を出力し、末尾で改行せよ。
入力例1
8 7 1 2 2 3 2 4 5 6 6 7 6 8 7 8
出力例1
1
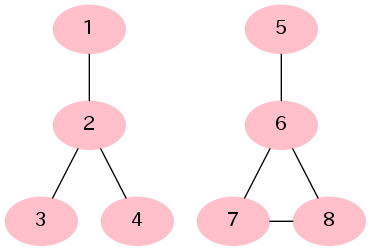
頂点 1, 2, 3, 4 からなる連結成分と頂点 5, 6, 7, 8 からなる連結成分の 2 つの連結成分がある。前者には閉路が含まれず、後者には閉路 6 - 7 - 8 - 6 が含まれる。従って、木であるような連結成分の個数は 1 である。
入力例2
5 1 1 2
出力例2
4
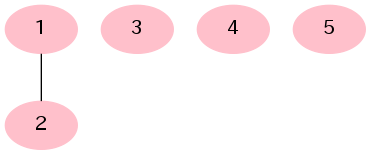
1 つの頂点からなる連結成分は木とみなされる。
入力例3
11 11 1 2 1 3 2 4 3 5 4 6 5 7 6 8 7 9 8 10 9 11 10 11
出力例3
0
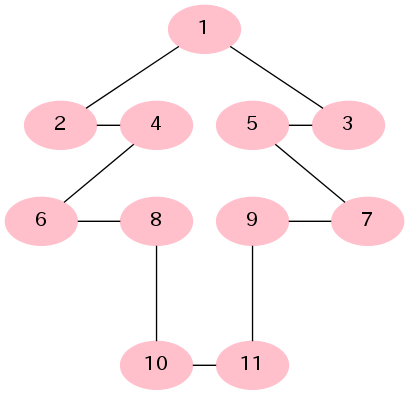
「木」を模したグラフではあるが、ここで問題となっている木ではない。
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君は「N^2マス計算」で計算力をつけることにした。「N^2マス計算」は N 行 N 列の表を用意して行う。 i 行目の左端のマスのさらに左には数 a_i が書かれており、 j 列目の上端のマスのさらに上には数 b_j が書かれている。高橋君はこの表の i 行 j 列目 に a_i × b_j の値を計算して書き込む。
すぐに解き終わってしまい退屈したので、高橋君は自分が書き込んだ N^2 個の値を昇順に並べ替えることにした。並べ替えた結果小さい方から K 番目 (1 番から数える) に位置する値を求めよ。
入力
入力は以下の形式で標準入力から与えられる。
N K a_1 a_2 .. a_N b_1 b_2 .. b_N
- 1 行目には、表の行数および列数 N (1 ≦ N ≦ 30000) と求めるべき値の並べ替え後の位置 K (1 ≦ K ≦ N^2) がスペース区切りで与えられる。
- 2 行目には、表の各行 i (1 ≦ i ≦ N) について、その行の左端のマスよりさらに左に書かれた数 a_i (1 ≦ a_i ≦ 10^9) がスペース区切りで与えられる。
- 3 行目には、表の各列 j (1 ≦ j ≦ N) について、その列の上端のマスよりさらに上に書かれた数 b_j (1 ≦ b_j ≦ 10^9) がスペース区切りで与えられる。
部分点
この問題には部分点が設定されている。
- 5 点分のテストケースは 1 ≦ N ≦ 10 を満たす。
出力
標準出力に、高橋君が表に書き込んだ N^2 個の値を昇順に並べ替えたとき小さい方から K 番目 (1 番から数える) に位置する値を出力し、末尾で改行せよ。
入力例1
2 3 2 3 3 5
出力例1
10
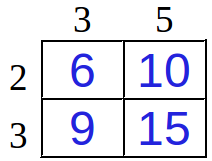
高橋君が書き込んだ値を昇順に並べ替えると 6, 9, 10, 15 となり、小さい方から 3 番目の値は 10 となる。
入力例2
3 7 1 2 1 2 1 2
出力例2
2
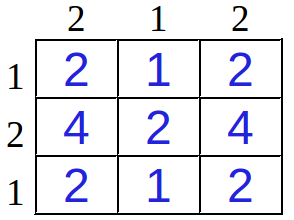
高橋君が書き込んだ値を昇順に並べ替えると 1, 1, 2, 2, 2, 2, 2, 4, 4 となり、小さい方から 7 番目の値は 2 となる。
入力例3
4 8 701687787 500872619 516391519 599949380 458299111 633119409 377269575 717229869
出力例3
317112176525562171
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
非負整数 L に対し、レベル L のシェルピンスキーのガスケットとは次のような図形である。
- レベル 0 のシェルピンスキーのガスケットとは、 1 個の正三角形である。
- レベル i (i ≧ 1) のシェルピンスキーのガスケットは、レベル i-1 のシェルピンスキーのガスケットに含まれる 3i-1 個の正三角形それぞれに対して以下の操作を行って得られる図形である。
(操作) 正三角形の各辺の中点を結び、中心に小さな正三角形を作る。この正三角形を図形から取り除く(この結果、もとの正三角形は 3 つの小さな正三角形に分割される)。
以下にレベル 0,1,2,3,4 のシェルピンスキーのガスケットを図示する。

正整数 L が与えられる。レベル L のシェルピンスキーのガスケットに含まれる 3L 個の正三角形のすべての辺を考える。これらの線分から形成される単純多角形 (自己交差しない多角形) の個数を 1,000,000,007 で割った余りを求めよ。相似な多角形であっても位置が異なるものは区別する。
以下に数えるべき多角形とそうでないものの例を示す。
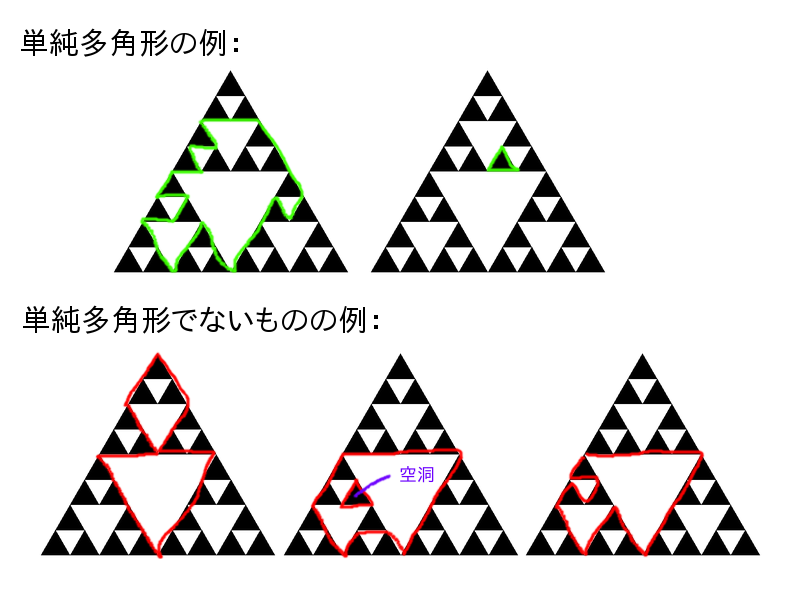
入力
入力は以下の形式で標準入力から与えられる。
L
- 1 行目に、 整数 L (1 ≦ L ≦ 105) が与えられる。
出力
標準出力に求める多角形の個数を 1,000,000,007 で割った余りを出力し、末尾で改行せよ。
入力例1
1
出力例1
11
以下の 11 個の単純多角形が存在する。

入力例2
2
出力例2
1033
入力例3
3
出力例3
30304092
入力例4
123
出力例4
853343829