Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
stove 君はとある平面世界の住人である。
ある日 stove 君は多くの金が取れる鉱山を砂漠とジャングルに発見した。
stove 君は 7 日間かけて鉱山採掘に取り組むことにした。
砂漠とジャングルは遠い位置関係にあるので、それぞれの日にはどちらか一方の鉱山でしか採掘できない。
その日の天候、気分に応じて採掘量が鉱山ごとに変化してしまうので、どちらの鉱山を選ぶべきかがその日毎に異なる場合がある。
それぞれの日においての採掘量が分かっているとき、最適に鉱山を選んだ場合に得られる金の量がいくらかを求めるプログラムを作成せよ。
入力
入力は以下の形式で標準入力から与えられる。
D_1 D_2 .. D_7 J_1 J_2 .. J_7
- 1 行目には、砂漠の鉱山に関する情報を表す 7 個の整数が空白区切りで書かれている。このうち左から i 番目の整数 D_i (0 ≦ D_i ≦ 2,000) は、i 日目に砂漠の鉱山で採掘を行った場合に得られる金の量が D_i キログラムであることを表す。
- 2 行目にはジャングルの鉱山に関する情報を表す 7 個の整数が空白区切りで書かれている。このうち左から i 番目の整数 J_i (0 ≦ J_i ≦ 2,000) は、i 日目にジャングルの鉱山で採掘を行った場合に得られる金の量が J_i キログラムであることを表す。
出力
最適に鉱山を選んだ場合に得られる金の量を 1 行に出力せよ。出力の末尾にも改行を入れること。
入力例1
4 2 0 5 6 2 5 6 1 4 3 6 4 6
出力例1
33
以下のように行動すれば良い。
- 1 日目にはジャングルの鉱山を選び、6 キログラムの金を得る。
- 2 日目には砂漠の鉱山を選び、2 キログラムの金を得る。
- 3 日目にはジャングルの鉱山を選び、4 キログラムの金を得る。
- 4 日目には砂漠の鉱山を選び、5 キログラムの金を得る。
- 5 日目には砂漠の鉱山を選び、6 キログラムの金を得る。
- 6 日目にはジャングルの鉱山を選び、4 キログラムの金を得る。
- 7 日目にはジャングルの鉱山を選び、6 キログラムの金を得る。
このように行動すると、6 + 2 + 4 + 5 + 6 + 4 + 6 = 33 キログラムの金を得ることができる。なお、5 日目にジャングルの鉱山を選んでも同じ量を達成することができる。
入力例2
1 2 3 4 5 6 7 2 3 4 5 6 7 8
出力例2
35
ジャングル一択である。
入力例3
0 0 0 0 0 0 0 0 0 0 0 0 0 0
出力例3
0
この例の場合、金を得ることができない。金が出るという話はなんだったのだろうか。
入力例4
8 3 0 2 5 25 252 252 252 2 5 2 5 2
出力例4
793
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
縦 H マス、横 W マスのチョコレートがある。各マスはブラックチョコかホワイトチョコである。ブラックチョコ同士、ホワイトチョコ同士は辺を共有しない(つまり、チョコレートは市松模様を形成している)。 各マスごとにチョコレートの濃度が定まっている。チョコレートの例を以下に表す(数字は濃度を表す)。

妹はこのチョコレートから、ある長方形領域を切り出して溶かし、チョコクリームを作成することにした。妹はチョコレートの味にこだわりを持っており、チョコクリームに使用されたブラックチョコとホワイトチョコの濃度の合計値(ただし、それぞれ使用されていない場合は濃度の合計値を 0 として扱うものとする)が等しくなければ気が済まない。
妹は条件を満たす切り出し方のうち、使用するチョコレートのマス数が最大でいくつになるのかが知りたい。
入力
入力は以下の形式で標準入力から与えられる。
H W
C_{1,1} C_{1,2} .. C_{1,W}
C_{2,1} C_{2,2} .. C_{2,W}
:
C_{H,1} C_{H,2} .. C_{H,W}
- 1 行目には、チョコレートの縦のマス数 H (1 ≦ H ≦ 100) および横のマス数 W (1 ≦ W ≦ 100) が空白区切りで与えられる。
- 2 行目から H 行では、濃度についての情報が与えられる。各行には W 個の非負整数が空白区切りで与えられる。i 行目の左から j 個目の整数 C_{i,j} (0 ≦ C_{i,j} ≦ 99) は左上隅を基準として、上から i 番目、左から j 番目のマスの濃度を表す。
出力
条件を満たす切り出し方が存在するなら、その中で使用するマス数の最大値を、存在しないなら 0 を出力せよ。出力の末尾にも改行を入れること。
入力例1
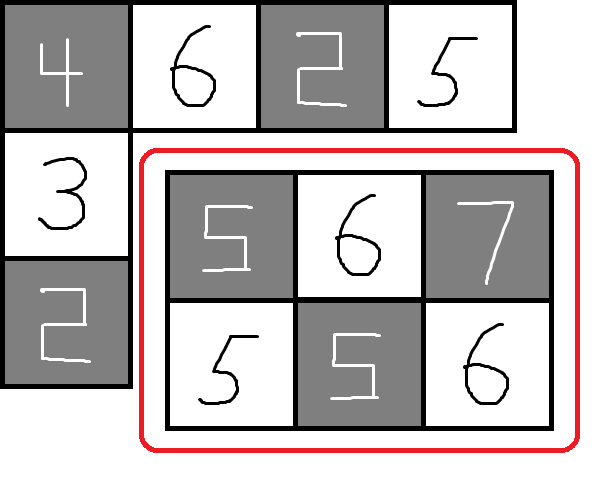
3 4 4 6 2 5 3 5 6 7 2 5 5 6
出力例1
6
下図のように縦 2 マス、横 3 マスの長方形領域を切り出せば、マス数が 6 となり、濃度の合計も 17 ずつと条件を満たす。
入力例2
2 2 4 0 7 3
出力例2
4
濃度が 0 である場合が含まれることに注意せよ。
入力例3
2 3 0 0 0 1 2 3
出力例3
3
入力例4
3 3 1 2 3 6 5 4 7 8 9
出力例4
0
この例において、条件を満たす切り出し方は存在しない。
入力例5
1 5 0 1 2 3 4
出力例5
1
ブラックチョコかホワイトチョコの一方のみを切り出す場合でも条件を満たす場合が存在することに注意せよ。
Time Limit: 7 sec / Memory Limit: 256 MiB
問題文
ウサギとカメが ARC 山でレースをすることになった。
ARC 山には N 個の中継点があり、中継点には 1 から N まで番号が付けられている。また異なる 2 つの中継点間を結ぶ道が M 本ある。どの 2 つの異なる道に関しても、結んでいる 2 つの中継点同士が一致することはない。道ごとに長さが定まっている。また、ARC 山にあるどの 2 つの異なる中継点についても、いくつかの道を経由することで行き来することができる。
レースでは、中継点の中から、目的地 A、ウサギのスタート地点 B、カメのスタート地点 C を選択する。A,B,C は中継点のうち 1 つでなければならず、A,B,C は互いに異なる必要がある。レースが始まると、ウサギは毎秒 R メートル、カメは毎秒 T メートルで目的地に進む。
カメは、カメが最適な移動を行うことでウサギがどの経路を使用してもカメより後に目的地に辿り着くような A,B,C の組 (A,B,C) が全部でいくつあるのかが知りたい。
入力
入力は以下の形式で標準入力から与えられる。
N M R T a_1 b_1 c_1 a_2 b_2 c_2 : a_M b_M c_M
- 1 行目には、中継点の個数 N (3 ≦ N ≦ 2,500)、道の本数 M (2 ≦ M ≦ 3,000)、ウサギの速さ R (1 ≦ R ≦ 200) およびカメの速さ T (1 ≦ T ≦ 200) が空白区切りで与えられる。
- 2 行目から M 行では、道についての情報が与えられる。このうち i 行目では、道 i が 2 つの中継点 a_i,b_i (1 ≦ a_i < b_i ≦ N) を結んでいて、長さが c_i (1 ≦ c_i ≦ 100) メートルであることを表す。
出力
組み合わせの総数を 1 行に出力せよ。出力の末尾に改行を入れること。
入力例1
4 5 2 1 1 2 4 1 3 3 1 4 6 2 3 5 3 4 4
出力例1
2
以下の 2 通りが考えられる。
- (目的地,ウサギのスタート地点,カメのスタート地点)を (2, 4, 1) とした場合、カメは直接目的地に向かうと 4 秒で到着する。一方ウサギはどのように経路をたどっても少なくとも 4.5 秒かかってしまう。
- (目的地,ウサギのスタート地点,カメのスタート地点)を (4, 3, 2) とした場合、カメは直接目的地に向かうと 4 秒で到着する。一方ウサギはどのように経路をたどっても少なくとも 4.5 秒かかってしまう。
以上の 2 通りとなる。因みに(目的地,ウサギのスタート地点,カメのスタート地点)を (1, 4, 3) とした場合、ウサギもカメも目的地に到達するには 3 秒以上必要となる。お互いに最適に移動した場合、同時に到着するので条件を満たさない。
入力例2
5 4 7 7 1 2 1 2 3 1 3 4 1 4 5 1
出力例2
26
Time Limit: 10 sec / Memory Limit: 512 MiB
問題文
Anti Real Corporation 社は、日々の生活をちょっと変わった方法で充実させようと奮闘する組織である。
Anti Real Corporation 社のコンセント差込口はちょっと変わった形状をしている。コンセント差込口は縦に H 行、横に W 列の穴が並んだ形状をしている。コンセントプラグは、未使用の穴のうち、上下または左右に連続した 2 箇所を使用することができる。言い変えると、上から i 番目、右から j 番目の穴を (i,j) と呼ぶことにすると、
- (i,j) と (i+1,j) (1 ≦ i ≦ H-1, 1 ≦ j ≦ W) の 2 つの穴を選んで使用する。
- (i,j) と (i,j+1) (1 ≦ i ≦ H, 1 ≦ j ≦ W-1) の 2 つの穴を選んで使用する。
コンセントプラグを差し込むにあたって、複数のコンセントプラグが同じ穴を同時に共有したり、コンセントキャップ(後述)が付いている穴を使用することはできない。
社長はある日、コンセントへの差し込みに面白さを与えるため、N 日間、営業開始時刻に以下の動作のうちどちらか 1 つを行うことにした。
- 未使用な穴を 1 つ選び、その穴にコンセントキャップを差し込む。
- コンセントキャップが差し込まれている穴を 1 つ選び、コンセントキャップを取り除き未使用状態にする。
最初、どの穴も未使用であるとする。
社長は部長に、N 日間のそれぞれの営業日において、コンセントへの差し込み方が全部で何通りあるのかを記録し、最終日に調査結果を報告するよう指示した。組み合わせについて、コンセントプラグ同士、コンセントキャップ同士は区別しないものとし、コンセントプラグを 1 つも使用しないものも 1 通りとして数えるとする。
ところがこのことを締めきり直前まで忘れてしまっていた部長は、偶然にも残されていたコンセントキャップの履歴から、どうにかそれぞれの日についての結果を求めることにした。
すべての組み合わせを虱潰しに調べているようでは間に合わなさそうなので、開発班のあなたに、プログラムを書くように依頼があった。
入力
入力は以下の形式で標準入力から与えられる。
H W N S_1 T_1 S_2 T_2 : S_N T_N
- 1 行目には、コンセント差込口の形状を表す 2 つの整数 H (1 ≦ H ≦ 2) と W (1 ≦ W ≦ 10^{11}) が空白区切りで与えられる。これはコンセント差込口が縦 H 行横 W 列に穴が並んだ形状をしていることを表す。
- 2 行目には操作日程を表す整数 N (1 ≦ N ≦ 20,000) が与えられる。
- 3 行目から N 行では、操作についての情報が与えられる。このうち i 行目では、i 日目に行う動作を表す 2 つの整数 S_i (1 ≦ S_i ≦ H) と T_i (1 ≦ T_i ≦ W) が与えられる。これは、この日の営業開始時刻より前の段階で (S_i, T_i) が未使用なら、その日の営業開始時にコンセントキャップを差し込むことを、そうでないならコンセントキャップを取り除くことを表す。
部分点
この問題には部分点が設定されている。
- W ≦ 5,000 , N ≦ 3,000 を満たすデータセット 1 に正解した場合は、10 点が与えられる。
- W ≦ 100,000 , N ≦ 3,000 を満たすデータセット 2 に正解した場合は、上記とは別に 30 点が与えられる。
- 追加制約のないデータセット 3 に正解した場合は、上記とは別に 60 点が与えられる。
出力
N 行にわたって出力せよ。N 行のうち i 行目には、i 日目の営業開始時の操作後において、考えられるコンセントの配置の総数を 1000000007 (= 1,000,000,007) で割った余りを出力せよ。
入力例1
2 3 3 1 1 2 3 1 1
出力例1
10 5 10
第 1 日目の操作の後、以下のような配置になっている。この図において、六角形で表された場所はコンセントキャップがある場所であることを表す。
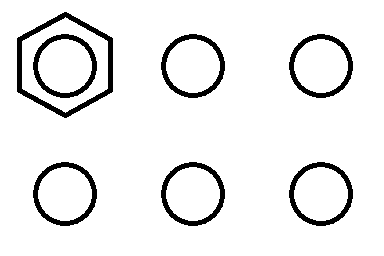
よって、以下の 10 通りの配置が考えられる。
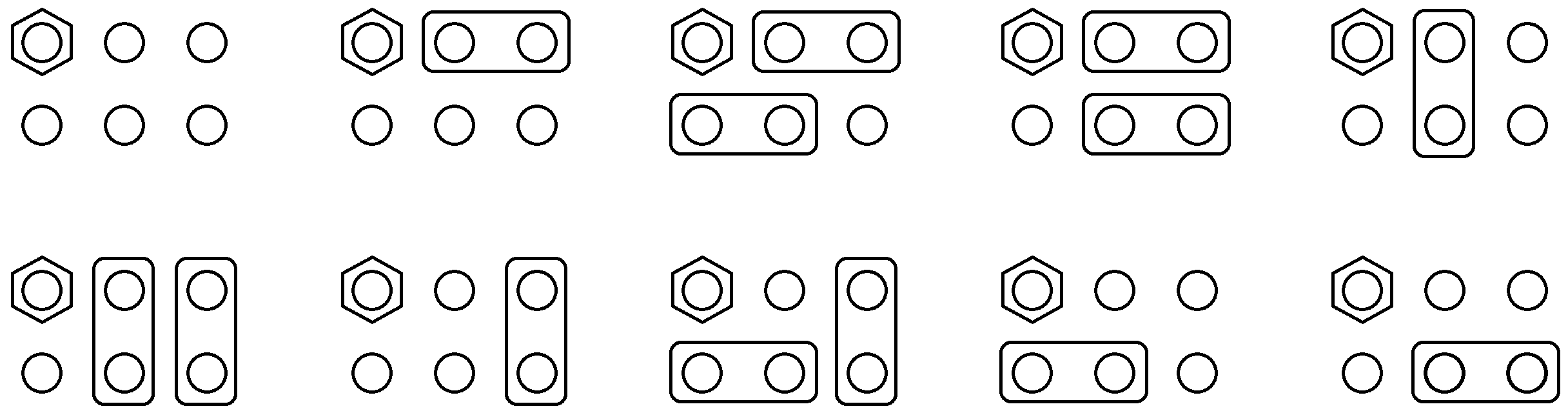
入力例2
2 4 5 1 2 1 1 2 2 2 1 1 4
出力例2
27 17 7 7 3