AtCoder Regular Contest 013

A - 梱包できるかな？

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

この春から新生活を始める今城くんは引越しを考えています。
そのため、自分の荷物をダンボールに梱包しなければなりませんが、今城くんの手元には１つのダンボールしかありません。
今城くんはこのサイズ N×M×L のダンボールに、サイズ P×Q×R の荷物をできるだけたくさん詰め込みたいです。
彼はこのダンボールにどれだけ荷物を詰め込むことができるでしょうか。

彼はとても几帳面な性格なので、荷物を全て同じ向きで梱包します。
さらに、今城くんは荷物が運送中に壊れることを防ぐため、斜めに入れることはありません。
つまり、荷物の少なくとも1つの面が、ダンボールか他の荷物のある面にぴったりとくっつくように梱包します。
ただし、荷物を横に90度倒すことはできます。

入力

入力は以下の形式で標準入力から与えられる。

N M L
P Q R

1 行目には整数 N 、 M 、L が与えられる。

N は今城くんが持っているダンボールのタテの長さです。
M は今城くんが持っているダンボールのヨコの長さです。
L は今城くんが持っているダンボールの高さです。
1≦N,M,L≦100 であることは保証されています。

2 行目には整数 P 、 Q 、R が与えられる。

P は今城くんが持っている荷物のタテの長さです。
Q は今城くんが持っている荷物のヨコの長さです。
R は今城くんが持っている荷物の高さです。
1≦P,Q,R≦100 であることは保証されています。

出力

今城くんがダンボールに詰め込むことができる荷物の数の最大値を 1 行で出力すること。
また、出力の最後には改行をいれること。

入力例 1

10 10 10
1 1 1

出力例 1

10*10*10のダンボールに、1*1*1の荷物を梱包すると、最大で1000個の荷物を梱包することができます。

入力例 2

10 3 1
2 1 1

出力例 2

10*3*1のダンボールに、2*1*1の荷物を梱包すると、最大で15個の荷物を梱包することができます。

入力例 3

5 10 3
2 5 3

出力例 3

5*10*3のダンボールに、2*5*3の荷物を梱包すると、そのままの向きでは、2*2*1の4つの荷物を梱包することができます。
ですが、この向きを変えて、5*2*3の荷物とみなすことで、最大5個の荷物を梱包することができます。

入力例 4

8 8 8
1 1 9

出力例 4

荷物を90度回転させることはできますが、傾けて入れることは出来ない為、この荷物を入れることは出来ません。

B - 引越しできるかな？

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

この春から新生活を始める今城くんは引越しを考えています。
そのため、自分の荷物をダンボールに梱包しなければなりません。
そこで、引越し業者「AtCoder株式会社」にダンボールを注文することにしました。

幸運なことに、AtCoder株式会社では「新生活応援キャンペーン」を行なっており、あるサイズのダンボールなら 1 種類だけ無料で提供しています。
これに目をつけた今城くんは、自分の荷物を全て梱包できるようなサイズのダンボールを大量に注文することで、お金を節約することにしました。
今城くんが注文しなければならないダンボールの容積の最小値はいくらでしょうか

また、今城くんは 1 つのダンボールに自分の荷物を 1 つだけ梱包します。
さらに、今城くんは荷物が運送中に壊れることを防ぐため、斜めに入れることはありません。
つまり、荷物の少なくとも1つの面が、ダンボールか他の荷物のある面にぴったりとくっつくように梱包します。

入力

入力は以下の形式で標準入力から与えられる。

C
N_{0} M_{0} L_{0}
N_{1} M_{1} L_{1}
:
N_{C-1} M_{C-1} L_{C-1}

入力 C+1 行ある。
1 行目には今城くんの荷物の数を表す整数 C(1≦C≦100) が与えられる。
2 行目から C+1 行目までの C 行では、今城くんの荷物のタテとヨコと高さがそれぞれ半角スペース区切りで与えられる。

N_{i} は今城くんが持っている荷物のタテの長さです。
M_{i} は今城くんが持っている荷物のヨコの長さです。
L_{i} は今城くんが持っている荷物の高さです。
1≦N_{i},M_{i},L_{i}≦100 かつ、それぞれの値は整数であることが保証されています。

部分点

1≦C≦10 を満たす入力にのみ正解した場合、部分点として 40 点が与えられる。

出力

今城くんが注文しなければならないダンボールの容積の最小値を 1 行で出力すること。
また、出力の最後には改行をいれること。

入力例 1

2
10 20 30
20 20 20

出力例 1

20*20*30のダンボールを用意すれば、すべての荷物を梱包することが可能です。

入力例 2

出力例 2

向きを変えて入れることにより、20*20*30のダンボールで梱包することが可能です。

入力例 3

出力例 3

これも向きを変えることにより、40*20*20のダンボールで梱包することが可能です。

入力例 4

2
10 10 10
11 1 1

出力例 4

荷物を傾けて入れることは出来ないので、11*10*10のダンボールが必要になります。

C - 笑いをとれるかな？

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

デビュー1年目の若手芸人「あっとこーだー」の高橋くんと青木くんは、地方ローカル番組に出演することになりました。
この番組では「ドキドキ☆ハバネロゲーム」というゲームが人気です。
以下が「ドキドキ☆ハバネロゲーム」の内容です。

参加する2人はお互いに直方体の豆腐を切り取って、切り取った部分を食べます。
ハバネロが含まれる部分を食べたほうが負けです。
高橋くんと青木くんはそれぞれ 1 回ずつ交互に切り取ります。
この豆腐のある部分にはハバネロが仕掛けられています。
豆腐は複数存在することがあります。
全ての豆腐にハバネロが必ず仕掛けられています。

高橋くんと青木くんはリアクション芸が苦手なので、ハバネロが含まれた部分を食べてしまうと視聴者の失笑を買うことはわかっています。
そのため、この2人は相方にハバネロを食べさせることで自分がすべることを全力で回避しようと考えています。

そこで、高橋くんと青木くんは相方に知られないように番組のプロデューサからハバネロの位置をこっそりと聞き出しました。
この2人が「ドキドキ☆ハバネロゲーム」において最善手を繰り返すとき、先にハバネロを食べてすべってしまうのはどちらでしょうか。
あなたは神の視点から、この滑稽な2人の行く末を高橋くんだけに教えることにしました。
なお、先攻は高橋くんで、豆腐の切り方は以下の通りです。

切り取り方は水平に 3 方向から切り取ることができます。つまり、斜めに切ることはできません。

豆腐の1辺の長さが必ず整数になるよう切断します。
例として、 2*2*2 の豆腐の切り方の一例を示します。

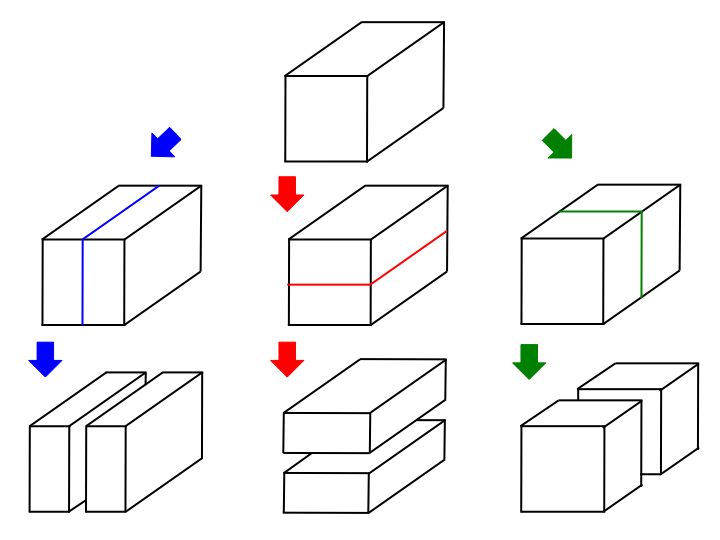
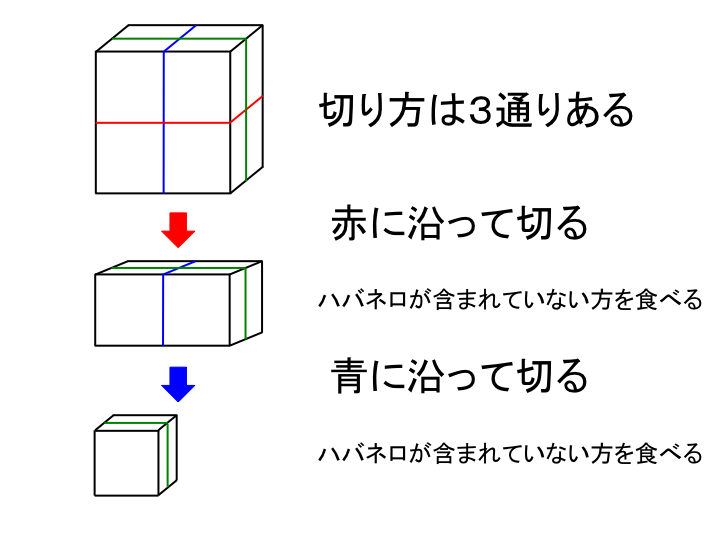
入力

入力は以下の形式で標準入力から与えられる。

N
X_{1} Y_{1} Z_{1}
M_{1}
x_{1,0} y_{1,0} z_{1,0}
x_{1,1} y_{1,1} z_{1,1}
:
x_{1,M_{1}-1} y_{1,M_{1}-1} z_{1,M_{1}-1}
X_{2} Y_{2} Z_{2}
M_{2}
x_{2,0} y_{2,0} z_{2,0}
x_{2,1} y_{2,1} z_{2,1}
:
x_{2,M_{2}-1} y_{2,M_{2}-1} z_{2,M_{2}-1}
:
X_{N} Y_{N} Z_{N}
M_{N}
x_{N,0} y_{N,0} z_{N,0}
x_{N,1} y_{N,1} z_{N,1}
:
x_{N-1,M_{N}-1} y_{N,M_{N}-1} z_{N,M_{N}-1}

1 行目には豆腐の数 N(1≦N≦1,000) が与えられる。
半角スペースで区切りで与えられる X_{i} Y_{i} Z_{i} は i 番目に与えられる豆腐のサイズで、

X_{i} は i 番目の豆腐のタテの長さ。
Y_{i} は i 番目の豆腐のヨコの長さ。
Z_{i} は i 番目の豆腐の高さ。
X_{i},Y_{i},Z_{i} はそれぞれ整数で、 1≦X_{i},Y_{i},Z_{i}≦1,000,000,000 であることが保証されている。

M_{i}(1≦M_{i}≦100) は i 番目の豆腐に仕掛けられてたハバネロの数です。
そのあと、半角スペースで区切りで与えられる x_{i,j} y_{i,j} z_{i,j} において

x_{i,j} は i 番目の豆腐に仕掛けられた j 番目のハバネロの x 座標
y_{i,j} は i 番目の豆腐に仕掛けられた j 番目のハバネロの y 座標
z_{i,j} は i 番目の豆腐に仕掛けられた j 番目のハバネロの z 座標
をそれぞれ示す。たとえば、座標 (1, 1, 1) にハバネロが仕掛けられた場合、下図のような位置にある。

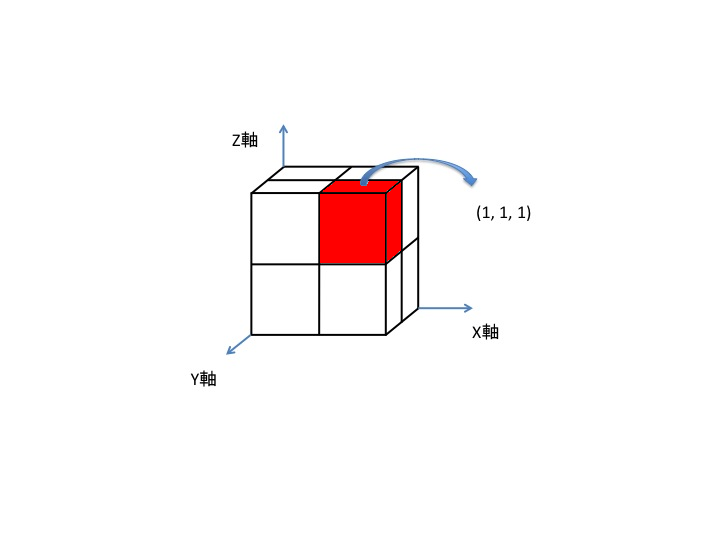
部分点

N = 1 かつ 1≦X_{i},Y_{i},Z_{i}≦20 を満たす入力にのみ正解した場合、部分点として 30 点が与えられる。

出力

先攻の高橋くんが勝利する場合はWINを、高橋くんが敗北する場合はLOSEを、それぞれ 1 行で出力すること。
また、出力の最後には改行をいれること。

入力例 1

出力例 1

WIN

高橋君が最初に x=0 の豆腐を食べてしまうことで、確実に勝つことができます。

入力例 2

出力例 2

LOSE

豆腐とハバネロの形が点対称になっているので、高橋君が食べた側と反対側の豆腐を食べられると、高橋君は絶対に勝つことができません。

入力例 3

出力例 3

LOSE

二つの豆腐は同じ形をしているので、高橋君が食べた豆腐と、反対側の豆腐を同じように食べられてしまうと、高橋君は絶対に勝つことができません。

D - 切り分けできるかな？

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

高橋君は道端に落ちていた鉄塊を切って分銅を作りたいです。
この鉄塊は特殊で、 1cm^3 で 1g であることが分かっていて、それを利用して分銅を作ります。
高橋君は心優しい青年なので、青木くんの分銅も作ってあげます。
また、高橋君は、あまり手先が器用ではないので、１つの鉄塊を切る回数を１回までとして、できるだけ多くの種類の分銅を作りたいと思いました。
鉄塊の切り方は以下の通りです。

鉄塊の1辺の長さが必ず整数になるように切断します。
切り取り方は水平に 3 方向から切り取ることができます。つまり、斜めに切断することはできません。

ただし、今回はある鉄塊を切断できる回数は 1 度のみです。
つまり、鉄塊 A を切断して鉄塊 B と鉄塊 C を得たならば、鉄塊 B と鉄塊 C を切断することはできません。

道端に落ちていた鉄塊の種類と、それぞれのサイズが与えられるので、高橋くんの分銅と青木くんの分銅を作成するのに必要な鉄塊の数はいくつでしょうか。

入力

入力は以下の形式で標準入力から与えられる。

N
X_{1} Y_{1} Z_{1}
X_{2} Y_{2} Z_{2}
:
X_{N} Y_{N} Z_{N}

1 行目には鉄塊の種類を示す整数 N(1≦N≦100) が与えられる。
2 行目から N+1 行までの N 行では、鉄塊の大きさが半角スペース区切りで与えられる。

X_{i} は i 番目の鉄塊のタテの長さ。
Y_{i} は i 番目の鉄塊のヨコの長さ。
Z_{i} は i 番目の鉄塊の高さ。
X_{i},Y_{i},Z_{i} はそれぞれ整数で、 1≦X_{i},Y_{i},Z_{i}≦20 であることが保証されている。

部分点

N = 1 を満たす入力にのみ正解した場合、部分点として 20 点が与えられる。

出力

全ての重さの分銅を作成するのに必要な鉄塊の数を 1 行で出力すること。
また、出力の最後には改行をいれること。

入力例 1

2
3 4 5
2 3 4

出力例 1

3*4*5の鉄塊からは、3*4の面に水平に切ると、12,24,36,48
3*5の面に水平に切ると、15,30,45
4*5の面に水平に切ると、20,40
と、９種類の分銅を作ることができます。
2*3*4の鉄塊からは、
2*3の面に水平に切ると、6,12,18
2*4の面に水平に切ると、8,16
3*4の面に水平に切ると、12
の５種類の分銅を作ることができます。
これらを合わせると１３種類の分銅が存在するので、これを二人分全て揃えたいです。
これは、3*4*5の鉄塊9個を、(12-48) (24-36) (36-24) (48-12) (15-45) (45-15) (30-30) (20-40) (40-20)と分け、
2*3*4の鉄塊4つを、(6-18) (18-6) (8-16) (16-8)の4つに切り分けることで、
二人分全種類の分銅を作ることができます。

入力例 2

1
3 1 1

出力例 2

入力例 3

2
2 2 1
6 2 1

出力例 3

入力例 4