AtCoder Regular Contest 004

A - 2点間距離の最大値 ( The longest distance )

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

平面上に N 個の点があり、それぞれ 0 から N-1 までの番号が付けられており、それぞれの点について x 座標と y 座標が与えられています。
その N 点のうち 2 点を選び結んで得られる線分のうち、最も長くなる線分の長さを求めてください。

入力

入力は以下の形式で標準入力から与えられる。

N
x_{0} y_{0}
x_{1} y_{1}
:
:
x_{N-1} y_{N-1}

入力は N+1 行ある。
1 行目には、点の個数を表す整数 N (2≦N≦100)が与えられる。
2 行目から N+1 行目までの i+2 (0 ≦ i < N) 行目には、i 番の点の x 座標を表す整数 x_{i}(0≦x_{i}≦100) と y 座標を表す整数 y_{i}(0≦y_{i}≦100) が空白を区切りとして与えられる。
与えられる点のうち x 座標と y 座標がともに一致する点の組は存在しないが、2 つの点を繋ぐ線分上に他の点が存在することはありうる。

出力

N 点のうち 2 点を選び結んで得られる線分のうち、最も長い線分の長さを標準出力に 1 行で出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 10^{-3} 以下であれば許容する。
なお、最後には改行を出力せよ。

入力例 1

出力例 1

3.605551

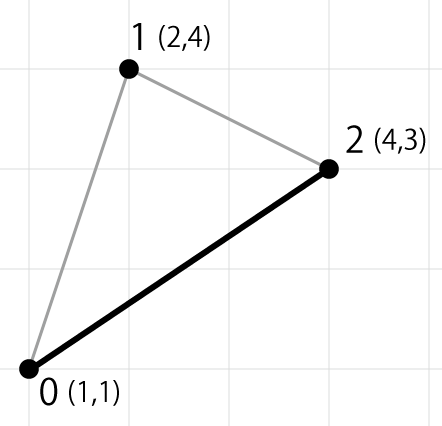
3 点の位置関係を示すと下図のようになります。

(1,1) と (2,4) を繋いだ線分の長さは \sqrt{(2-1)^2+(4-1)^2} = \sqrt{10} = 3.162278 です。
(2,4) と (4,3) を繋いだ線分の長さは \sqrt{(4-2)^2+(3-4)^2} = \sqrt{5} = 2.236068 です。
(4,3) と (1,1) を繋いだ線分の長さは \sqrt{(1-4)^2+(1-3)^2} = \sqrt{13} = 3.605551 です。
以上により最も長い線分の長さは太線が示す 3.605551 になります。

入力例 2

出力例 2

10.630146

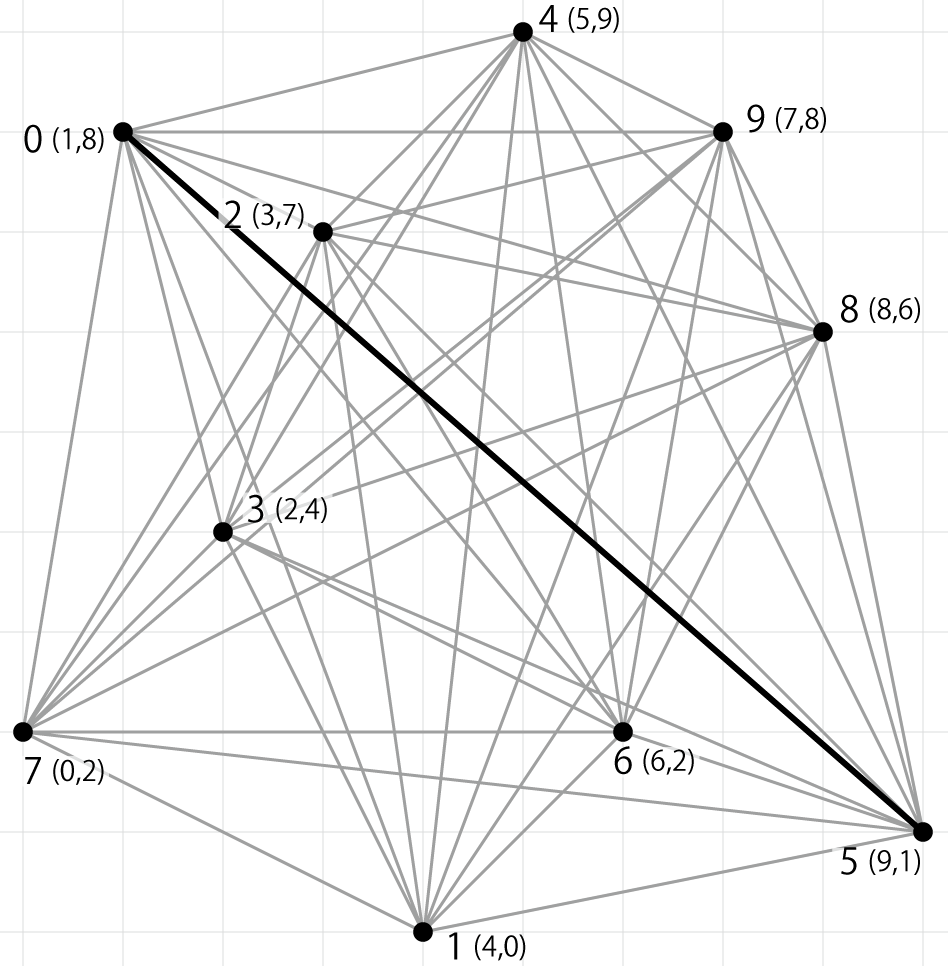
10 点の位置関係を示すと下図のようになります。
最も長い線分は点 0 と点 5 を繋ぐ線分で、10.630146 になります。

入力例 3

出力例 3

141.421356

最も長い線分は点 0 と点 3 を繋ぐ線分、または点 1 と点 2 を繋ぐ線分で、141.421356 になります。

入力例 4

出力例 4

4.000000

最も長い線分は点 2 と点 3 を繋ぐ線分で、その長さは 4.000000 です。

入力例 5

出力例 5

4.242641

最も長い線分は点 1 と点 3 を繋ぐ線分で、その長さは 4.242641 です。

Source Name

ARC 004

B - 2点間距離の最大と最小 ( Maximum and Minimum )

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

平面上に N+1 個の点があり、それぞれ 0 から N までの番号が付けられています。
それぞれの点の位置はわかりませんが、0 以上 N 未満の整数 i について、i 番の点と i+1 番の点の距離 d_i はわかっています。
0 番の点と N 番の点の距離としてとりうる値の最大と最小を求めてください。

入力

入力は以下の形式で標準入力から与えられる。

N
d_{0}
d_{1}
:
d_{N-1}

入力は N+1 行からなる。
1 行目には点の番号の最大を表す整数 N(1≦N≦500) が与えられる。
2 行目から N+1行目までの i+2 行目 (0 ≦ i < N)には、i 番と i+1 番の点の距離を表す整数 d_i(1≦d_i≦30,000) が与えられる。

出力

出力は標準出力に出力し、2 行からなる。
1 行目には、0 番の点と N 番の点の距離としてとりうる最大値を出力せよ。
2 行目には、0 番の点と N 番の点の距離としてとりうる最小値を出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 10^{-3} 以下であれば許容する。
なお、最後には改行を出力せよ。

入力例 1

1
1024

出力例 1

1024
1024

入力より 0 番の点と 1 番の点があり、それらの間の距離は 1024 であることが分かります。
求める距離は、0 番の点と 1 番の点の間の距離なので最大値も最小値もともに 1024 です。

入力例 2

出力例 2

12
0

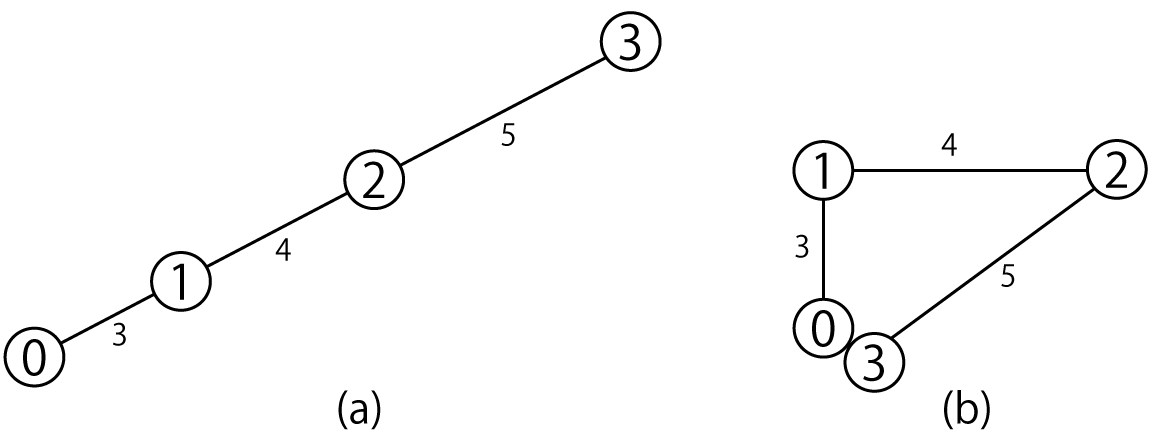
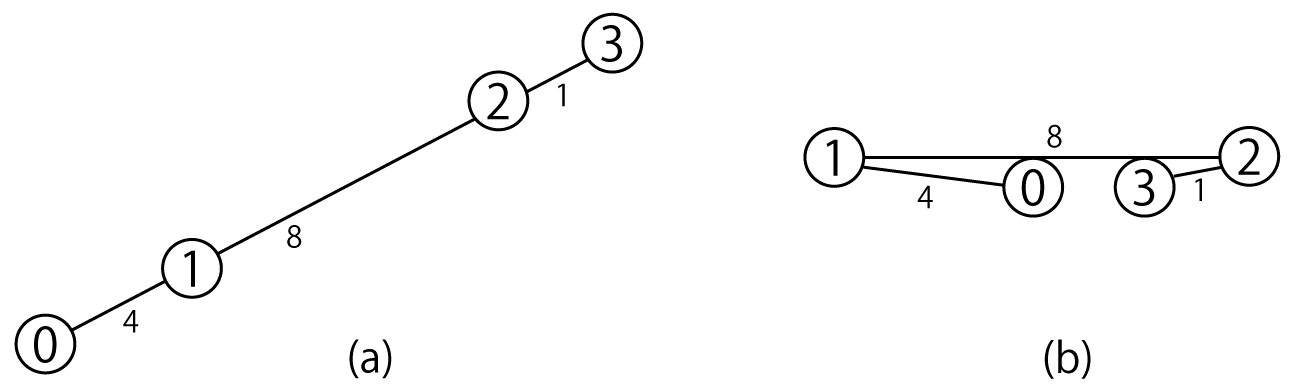
0 番の点と 3 番の点の間の距離が最も大きくなるのは、下図(a)のように 0 番の点と 3 番の点を端にして 4 点が一直線に並ぶ場合で、その距離は 3+4+5=12 となります。
0 番の点と 3 番の点の間の距離が最も小さくなるのは、下図(b)のように 0 番の点と 3 番の点の位置が等しい場合で、その距離は 0 となります。

入力例 3

2
512
512

出力例 3

1024
0

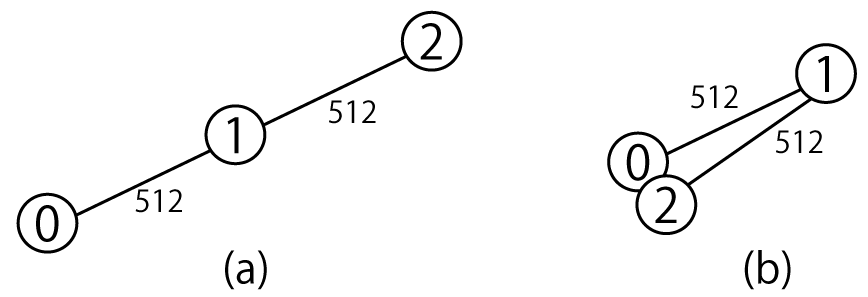
0 番の点と 2 番の点の間の距離が最も大きくなるのは、下図(a)のように 0 番の点と 2 番の点を端にして 3 点が一直線に並ぶ場合で、その距離は 512+512=1024 となります。
0 番の点と 2 番の点の間の距離が最も小さくなるのは、下図(b)のように 0 番の点と 2 番の点の位置が等しい場合で、その距離は 0 となります。

入力例 4

出力例 4

13
3

0 番の点と 3 番の点の間の距離が最も大きくなるのは、下図(a)のように 0 番の点と 3 番の点を端にして 4 点が一直線に並ぶ場合で、その距離は 4+8+1=13 となります。
0 番の点と 3 番の点は重なることができないので、0 番の点と 3 番の点の間の距離が最も小さくなるのは下図(b)のように 1 番の点と 2 番の点を繋ぐ線分上に 0 番の点と 3 番の点がある場合で、その距離は 8-4-1=3 となります。

入力例 5

出力例 5

55
0

0 番の点と 10 番の点の間の距離が最も大きくなるのは、0 番の点から 10 番の点が順に一直線に並ぶ場合で、その距離は 1+2+3+4+5+6+7+8+9+10=55 となります。
0 番の点と 10 番の点の間の距離が最も小さくなる一例は、0 番の点から 10 番の点まで順に円型に並び、0 番の点と 10 番の点の位置が等しくなった場合です。

Source Name

ARC 004

C - 平均値太郎の憂鬱 ( The melancholy of Taro Heikinchi )

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

太郎君は 1 から N までの正整数の平均値を求めようと思い、1 から N までの合計値を N で割ることにしました。
しかし、1 から N までの正整数を合計するときに、ある正整数 M(M は N 以下の正整数)だけ足し忘れてしまい、間違った平均値を算出してしまいました。
さらに、太郎君は正整数 N の値も忘れてしまいました。

今、間違った平均値だけがわかっています。元の数 N と M の組み合わせとして考えられるものを全て答えてください。

入力

入力は以下の形式で標準入力から与えられる。

X/Y

入力は 1 行のみからなり、間違った平均値が分数の形で与えられる。
分数は整数 X(1≦X≦10^{18})、/、整数 Y(1≦Y≦10^9) の順で与えられ、間違った平均値が X/Y であることを表す（0 < X/Y≦10^9）。
ただし、入力は既約分数とは限らない。

出力

N と M(1≦M≦N) の間に空白を区切りとして入れて、N と M の組み合わせとして考えられるものを全て N の値が小さい順に標準出力に出力せよ。
ただし、考えられる答えが複数ある場合は 1 行に N と M を 1 組ずつ出力し、考えられる答えが無い場合は Impossible と答えること。
なお、最後には改行を出力せよ。

入力例 1

4/3

出力例 1

3 2

N=3、M=2 の時、間違った平均値は (1+3)/3 = 4/3 となり、入力を満たします。
したがって、この組み合わせが答えとなります。

入力例 2

4/6

出力例 2

Impossible

入力値を満たすような解は存在しません。

入力例 3

49995/10

出力例 3

10000 10000

N=10,000、M=10,000 の時、間違った平均値は (1+2+...+9999)/10000 = 4995000/10000 = 49995/10 となり、入力を満たします。

入力例 4

1/400

出力例 4

Impossible

Source Name

ARC 004

D - 表現の自由 ( Freedom of expression )

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

整数 N と M が与えられる時、整数 N を M 個の整数の積で表す方法は何通りあるでしょうか。
その答えを 1,000,000,007 で割った余りを答えてください。

入力

入力は以下の形式で標準入力から与えられる。

N M

入力は 1 行のみからなり、整数 N(1 ≦ |N| ≦ 10^9) と整数 M(1 ≦ M ≦ 10^5) が空白区切りで与えられる。

出力

整数 N を M 個の整数の積で表す方法の数を 1,000,000,007 で割った余りを標準出力に 1 行で出力せよ。
なお、最後には改行を出力せよ。

入力例 1

10 2

出力例 1

10 を 2 つの整数の積で表す方法は以下の 8 通りになります。

1 \times 10
2 \times 5
5 \times 2
10 \times 1
(-1) \times (-10)
(-2) \times (-5)
(-5) \times (-2)
(-10) \times (-1)

入力例 2

1000000000 1

出力例 2

1,000,000,000 を 1 つの積で書き表すには 1,000,000,000 と書くしか無いので、1 通りになります。

入力例 3

-2 3

出力例 3

-2 を 3 つの整数の積で表す方法は以下の 12 通りになります。

1 \times 1 \times (-2)
1 \times 2 \times (-1)
1 \times (-1) \times 2
1 \times (-2) \times 1
2 \times 1 \times (-1)
2 \times (-1) \times 1
(-1) \times 1 \times 2
(-1) \times 2 \times 1
(-1) \times (-1) \times (-2)
(-1) \times (-2) \times (-1)
(-2) \times 1 \times 1
(-2) \times (-1) \times (-1)

入力例 4

50 1000

出力例 4

96554651

Source Name

ARC 004