AtCoder Regular Contest 003

A - GPA計算

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

高橋君はアメリカに留学しようと考えており、成績表を提出することになりました。
アメリカ留学の成績表には、学力を測る指標であるGPAを表記する必要があります。
GPAとは各単位に対する評価(A,B,C,D,F)を点数に換算して平均した値で、点数への換算は以下のようになります。

A評価 → 4 点
B評価 → 3 点
C評価 → 2 点
D評価 → 1 点
F評価 → 0 点

全てF評価だった場合は、GPAは 0 になります。
高橋君の各単位に対する評価をもとにGPAを求めなさい。

入力

入力は以下の形式で標準入力から与えられる。

N
r_{1}r_{2}...r_{N}

1 行目は、単位の総数を表す整数 N (1 ≦ N ≦ 100) が与えられる。
2 行目には、単位に対する評価を表す N 文字の文字列が与えられる。
i 文字目の文字 r_{i} は A, B, C, D, F のいずれかである。

出力

入力として与えられた単位の評価をもとにしたGPAを標準出力に 1 行で出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 1e-9 以下であれば許容する。(1e-9=10^{-9})
なお、最後には改行を出力せよ。

入力例 1

34
ABABAAABACDDDABADFFABABDABFAAABFAA

出力例 1

2.79411764705882

各評価の個数は以下のようになります。

A評価 … 16 個
B評価 … 8 個
C評価 … 1 個
D評価 … 5 個
F評価 … 4 個

したがって、点数の総和は 4×16+3×8+2×1+1×5+0×4=95 になり、平均は 95÷34=2.79411764705882 です。

入力例 2

5
FFFFF

出力例 2

F評価が 5 つなのでGPAは (0×5)÷5=0 になります。

Source Name

ARC 003

B - さかさま辞書

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

高橋君は友達とチャットで逆さしりとりをすることにしました。
逆さしりとりとは、前の人が言った単語の頭文字で終わる単語を答えるしりとりです。
しかし、高橋君は英単語に自信がないのでこっそり「さかさま辞書」を使うことにしました。

普通の辞書は単語の先頭の文字がABC順になるように並べられており、同じ文字同士の場合はその次の文字がABC順になるように並べられます。
先頭から見ていく普通の辞書順に対して、「さかさま辞書」は後ろの文字から見ていきます。
例えば apple, bee, card は、普通の辞書なら apple → bee → card の順になります。
しかし、「さかさま辞書」では d で終わる card が 1 番、apple とbee は同じ e で終わるのでその 1 つ前が e である bee が 2 番、l であるapple が 3 番の順になります。

図(a)：普通の辞書順に並べた例　　図(b)：さかさま辞書順に並べた例

高橋君の代わりに「さかさま辞書」を作成し、与えられた単語を「さかさま辞書」順に並べてください。

入力

入力は以下の形式で標準入力から与えられる。

N
s_{1}
s_{2}
:
:
s_{N}

1 行目は、並べる単語数を表す整数 N (1 ≦ N ≦ 100) が与えられる。
2 行目から N 行は、並べる単語を表す文字列が 1 行に 1 つずつ与えられる。
i+1 行目の文字列 s_i の長さは 1 文字以上 20 文字以下で、含まれる文字はアルファベットの小文字のみ(a-z)です。
なお、重複する単語が与えられることはありません。

出力

入力として与えられた単語を、さかさま辞書順に標準出力に 1 行ずつ出力せよ。
なお、最後には改行を出力せよ。

入力例 1

5
chokudai
kensho
imos
yuichirw
ao

出力例 1

chokudai
ao
kensho
imos
yuichirw

まず、それぞれの一番後ろの文字は、chokudai、kensho、imos、yuichirw、aoなのでABC順に並べると、i,o,s,wの順になります。
しかしkenshoとaoの 2 人が同じ o なので、この 2 人に関してはその 1 つ前の文字の順で並べます。
kenshoの後ろから 2 つ目の文字は h、ao の後ろから 2 つ目の文字は a なので、ao, kensho の順になります。
よって、chokudai, ao, kensho, imos, yuichirw の順が答えになります。

入力例 2

2
dart
art

出力例 2

art
dart

後ろから 1,2,3 番目とも同じ文字なので、後ろから 4 番目の文字を比較します。
しかし、art の後ろから 4 番目の文字はありません。
無い場合は、a よりも早いので、art, dart の順になります。

Source Name

ARC 003

C - 暗闇帰り道

Time Limit: 5 sec / Memory Limit: 64 MB

問題文

高橋君は、夜道を通って学校から自宅へと 1 人で帰ろうとしています。
彼の住む街は長方形の形をしており、格子状の区画に区切られています。彼は東西南北に 1 秒に 1 区画ずつ移動することができます。
各区画には日当たりの良さが与えられ、経過時間 t 秒(出発時間は 0 秒)を用いて「“各区画の明るさ” ＝ 日当たりの良さ × 0.99^t」と表すことが出来ます。
学校から自宅まで帰る途中に通る経路上の区画における“区画の明るさ”の最小値を、その経路における“経路の明るさ”とします。
高橋君は暗所恐怖症なので、“経路の明るさ”がなるべく大きい経路を選択したいと考えています。
そのような経路を選択した場合の、“経路の明るさ”を求めなさい。

入力

入力は以下の形式で与えられる。

N M
c_{11}c_{12}…c_{1M}
c_{21}c_{22}…c_{2M}
:
:
c_{N1}c_{N2}…c_{NM}

1 行目は、街の南北の長さとして整数 N(1≦N≦500) と東西の長さとして整数 M(1≦M≦500) が空白で区切られて与えられる。
2 行目から N 行は、格子状の街の各区画における状態 c_{ij} がそれぞれ s, g, 1-9, # のいずれかで与えられる。
i+1 行目 j 文字目の文字 c_{ij} は、座標 (j,i) が下記のような状態であることを表す。
- s : その区画が学校であることを表す。
- g : その区画が自宅であることを表す。
- 1-9 : その区画の日当たりの良さを表す。
- # : その区画に侵入出来ないことを表す。
与えられた街の外を通ることは出来ない。
s と g はそれぞれ 1 つずつ与えられ、s と g は隣接していない。

出力

“経路の明るさ”の最大値を標準出力に 1 行で出力せよ。
学校から自宅に帰る経路が存在しない場合は -1 と 1 行で出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 1e−9 以下であれば許容する。
なお、最後には改行を出力せよ。

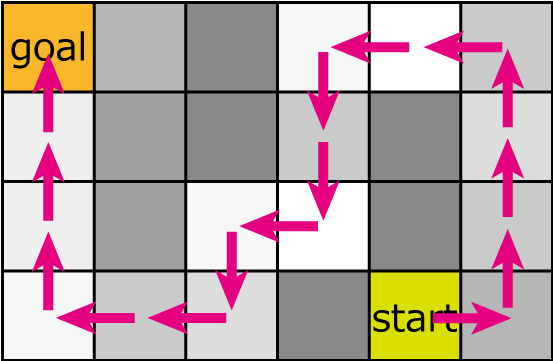
入力例 1

出力例 1

2.910897

時刻0: 学校 (1,1) を出発します。
時刻1: (2,1) に移動します。時刻 t=1, 日当たりの良さ=7 なので、(2,1) の明るさは 6.93 です。
時刻2: (2,2) に移動します。時刻 t=2, 日当たりの良さ=4 なので、(2,2) 明るさは 3.9204 です。
時刻3: (2,3) に移動します。時刻 t=3, 日当たりの良さ=3 なので、(2,3) 明るさは 2.910897 です。
時刻4: 自宅 (3,3) に移動します。ここまで一番暗かったのは、時刻 t=3 の (2,3) における明るさ 2.910897 なので、答えは 2.910897 となります。

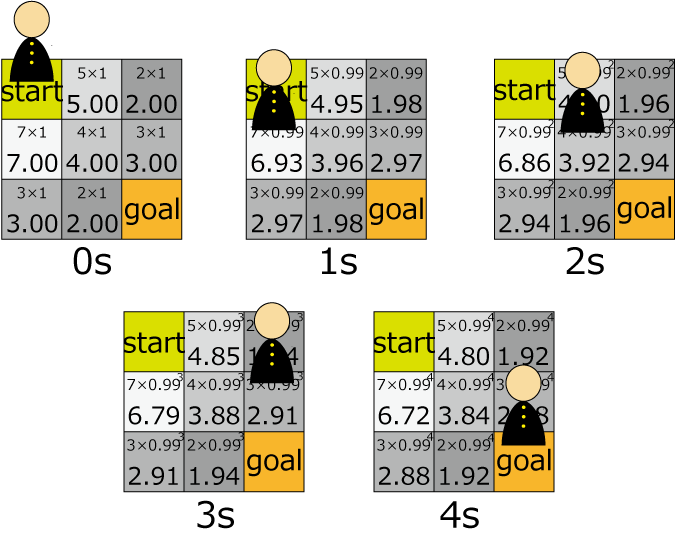
入力例 2

出力例 2

2.97

下記のようなルートを通る時、明るさが 2.97 となり、これが最善となります。

Source Name

ARC 003

D - シャッフル席替え

Time Limit: 10 sec / Memory Limit: 64 MB

問題文

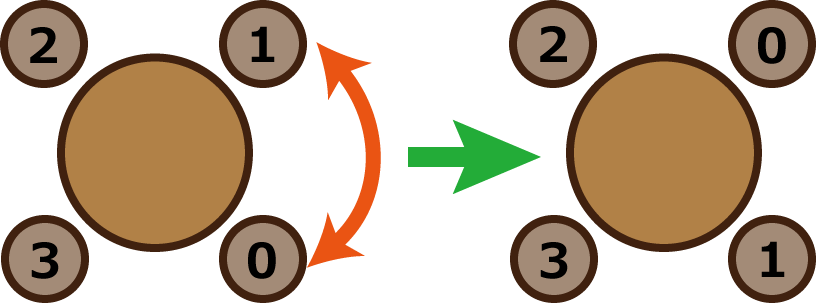
高橋君が働くAtCoder社では、いつも 1 つの円形のテーブルの周囲に社員全員で座ってミーティングを行います。
それぞれお気に入りの席があるのでいつも席は同じなのですが、今日は席替えをすることにしました。
高橋君がランダムに 2 人を選び場所を入れ替える動作を決められた回数行った後の席配置が新しい席配置になります。
しかし、残念なことにAtCoder社には隣り合わせにしてしまうとミーティング中におしゃべりをしてミーティングを邪魔してしまう 2 人組が存在します。
高橋君は真面目なので、ミーティングが滞りなく行われるようにそのような 2 人組は 1 組も隣り合わせにしたくないと思っています。
席替えを行った後に、隣り合わせにしてはいけない 2 人組が 1 組も隣り合わない確率を求めなさい。

入力

入力は以下の形式で与えられる。

N M K
A_{1} B_{1}
A_{2} B_{2}
: :
: :
A_{M} B_{M}

1 行目は、社員の総数として整数 N (2 ≦ N ≦11)、隣り合わせにしてはいけない 2 人組の組数として整数 M (0 ≦ M ≦ 10)、入れ替える回数として整数 K (0 ≦ K ≦ 20) が空白で区切られて与えられる。
2 行目から M 行は、1 行に 1 組ずつ隣り合わせにしてはいけない 2 人が空白で区切られて与えられる。
i+1 行目の整数 A_{i} と整数 B_{i} (0 ≦ A_{i} < B_{i} < N) は、隣り合わせにしてはいけない 2 人を表し、それぞれ高橋君から見て右に何人目であるかを表す。
なお A_i = 0 または、B_i = 0 の場合は高橋君自身を表す。

出力

ちょうど K 回の入れ替えを行った後に、隣同士にしてはいけない 2 人組が 1 組も隣り合っていない確率を標準出力に 1 行で出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 2e−3 以下であれば許容する。
なお、最後には改行を出力せよ。

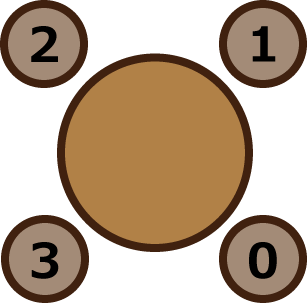
入力例 1

4 1 1
0 3

出力例 1

0.333333333333

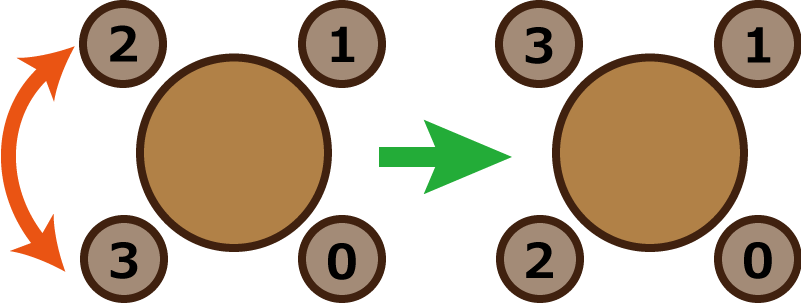
席替えを行う前は、4 人の配置は下図のようになっています。

1 回入れ替えるという席変えを行った時、0 と 3 の 2 人が隣合わないようにするには、

0 と 1 を入れ替える。

2 と 3 を入れ替える。

の 2 通りです。4 人から 2 人を選ぶ方法は 6 通り存在するので、条件を満たす確率は 2/6 となり答えは 1/3 です。

入力例 2

出力例 2

高橋君以外の 4 人のうち、高橋君と隣り合うことのできる人が 1 人も存在しないので、条件を満たすことはありません。

入力例 3

5 1 2
0 3

出力例 3

0.52

2 回の入れ替えの後、0 と 3 が隣り合わない入れ替え方法は 52通りあります。
5 人から 2 人を選ぶことを 2 回行うと全ての組み合わせは (_5C_2)^2 = 10^2 = 100 通りになります。
したがって、答えは 52÷100 = 0.52 です。

Source Name

ARC 003