実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1000 点
問題文
数直線の上に N 個のりんごと N 個の箱があります。具体的には、座標 A_1, \dots, A_N にりんごが、座標 B_1, \dots, B_N に箱が置かれています。
りんごの箱詰めを担当する AtCoder さんは、ロボットアームを操作してりんごを箱の中に入れます。ロボットアームは最初座標 0 にあり、数直線上で自由に動かすことができます。ロボットアームがりんごのある座標にいるとき、そのりんごをつかむことができ、箱のある座標にいるとき、ロボットアームがつかんだりんごを離してその箱に入れることができます。ただし、ロボットアームは同時にひとつしかりんごを持つことができず、各箱にはひとつしかりんごを入れることができません。特定のりんごを特定の箱に入れなければならないといった制限はありません。
作業時間の制約上、ロボットアームの移動距離の合計は T 以下でなくてはなりません。また、作業終了時にロボットアームが座標 0 に戻っている必要があります。このとき、最大でいくつのりんごを箱に入れることができるでしょうか?
制約
- 1 \leq N \leq 4\,500
- 0 \leq T \leq 10^{14}
- 1 \leq A_1 < A_2 < \cdots < A_N \leq 10^{10}
- 1 \leq B_1 < B_2 < \cdots < B_N \leq 10^{10}
- A_1, A_2, \dots, A_N, B_1, B_2, \dots, B_N はすべて異なる
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられます。
N T A_1 A_2 \cdots A_N B_1 B_2 \cdots B_N
出力
答えを出力してください。
入力例 1
3 12 1 2 3 4 5 6
出力例 1
2
以下のようにロボットアームを動かすと、2 つのりんごを箱に入れることができます。
- ロボットアームを座標 0 から座標 1 に動かし、そこにあるりんごをつかむ。
- ロボットアームを座標 1 から座標 4 に動かし、そこにある箱にりんごを入れる。
- ロボットアームを座標 4 から座標 3 に動かし、そこにあるりんごをつかむ。
- ロボットアームを座標 3 から座標 5 に動かし、そこにある箱にりんごを入れる。
- ロボットアームを座標 5 から座標 0 に動かす。
動かす距離は 12 であるため、条件を満たしています。
入力例 2
3 11 1 2 3 4 5 6
出力例 2
1
以下のようにロボットアームを動かすと、1 つのりんごを箱に入れることができます。
- ロボットアームを座標 0 から座標 2 に動かし、そこにあるりんごをつかむ。
- ロボットアームを座標 2 から座標 5 に動かし、そこにある箱にりんごを入れる。
- ロボットアームを座標 5 から座標 5.2 に動かす。
- ロボットアームを座標 5.2 から座標 0 に動かす。
動かす距離は 10.4 であるため、条件を満たしています。
入力例 3
5 18000000000 1000000000 1000000001 1000000002 9999999997 9999999998 5000000000 5000000001 5000000002 9999999999 10000000000
出力例 3
2
実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 1000 点
問題文
AtCoder さんには、N 件の会議の予定が入っています。
会議は優先度の高い順に 1 から N までの番号が付けられており、 会議 i は時刻 L_i から時刻 R_i までの時間帯に完全に含まれる、連続する好きな 1 単位時間を選んで行うことができます。 ただし、同時に複数の会議に出席することはできません。
AtCoder さんはできるだけ長い睡眠時間を確保したいので、出席する最初の会議が始まってから、出席する最後の会議が終わるまでの時間を最小化したいです。 また、最小化する方法が複数ある場合、最後の会議が終わる時刻をできるだけ早くしたいです。
k = 1, 2, \dots, N について、次の問いに答えてください。
- 会議 1 から k までに出席するとき、k 件すべての会議に出席できるかどうかを判定し、もし可能であれば最適な戦略をとった場合における、最初の会議が始まる時刻と最後の会議が終わる時刻をそれぞれ求めよ。
制約
- 1 \leq N \leq 180\,000
- 0 \leq L_i < R_i \leq 180\,000
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられます。
N L_1 R_1 L_2 R_2 \vdots L_N R_N
出力
N 行にわたって出力してください。
k 行目 (1 \leq k \leq N) には、会議 1 から会議 k まで出席するケースについて、以下の形式で出力してください。
- k 件すべての会議に出席できる場合: 最初の会議の開始時刻と、最後の会議の終了時刻を空白区切りで出力
- k 件すべての会議に出席できない場合:
Impossibleを出力
入力例 1
3 5 7 2 4 1 6
出力例 1
5 6 3 6 3 6
たとえば、会議 1, 2, 3 すべてに出席する場合、以下のような戦略が最適になります。
- 会議 2 の開始時刻を 3、終了時刻を 4 に設定する。
- 会議 3 の開始時刻を 4、終了時刻を 5 に設定する。
- 会議 1 の開始時刻を 5、終了時刻を 6 に設定する。
入力例 2
2 0 1 179999 180000
出力例 2
0 1 0 180000
入力例 3
7 10 15 10 15 10 15 10 15 10 15 10 15 10 15
出力例 3
10 11 10 12 10 13 10 14 10 15 Impossible Impossible
入力例 4
8 15 18 17 20 15 20 15 20 10 13 11 15 11 13 10 13
出力例 4
15 16 16 18 15 18 15 19 12 19 12 19 11 19 10 19
入力例 5
20 6 13 5 20 9 15 23 24 7 10 10 11 6 13 6 17 7 21 12 22 9 17 7 19 7 18 6 22 20 24 11 13 16 24 14 18 12 25 19 21
出力例 5
6 7 5 7 7 10 12 24 9 24 9 24 9 24 9 24 9 24 9 24 9 24 9 24 9 24 9 24 9 24 8 24 7 24 6 24 5 24 5 25
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1000 点
問題文
AtCoder さんは、n 問の問題からなるテストを受験しました。 このテストでは、1 問ずつ問題が出題されていきますが、出題される問題の難易度は現時点での正解状況に応じて変化し、具体的には以下のようになります。
- 現時点の正解数が、現時点での不正解数以上である場合、AtCoder さんは確率 1/3 で次の問題に正解する。
- 現時点の正解数が、現時点での不正解数未満である場合、AtCoder さんは確率 2/3 で次の問題に正解する。
- ここで、各問題の正解・不正解の確率は独立であると仮定する。すなわち、問題を解くときに確率 1/3 あるいは確率 2/3 で表が出るコインを振り、表が出たら正解すると考えて良い。
過半数の問題に正解すれば合格です。
さて、AtCoder さんが合格する確率を 3^n 倍した値 f(n) は整数になります。
整数 N が与えられるので、 \sum_{n=1}^{N} \lfloor \frac{10^{18}}{n} \rfloor \times f(n) を 10^9 + 7 で割った余りを計算してください。
制約
- 1 \leq N \leq 10\,000\,000
- N は整数
入力
入力は以下の形式で標準入力から与えられます。
N
出力
答えを出力してください。
入力例 1
2
出力例 1
500000077
問題数が 1 問のときの合格確率は \frac{1}{3}、2 問のときの合格確率は \frac{1}{9} であるため、
- \lfloor \frac{10^{18}}{1} \rfloor \times \left(\frac{1}{3} \times 3^1\right) + \lfloor \frac{10^{18}}{2} \rfloor \times \left(\frac{1}{9} \times 3^2\right) = 1.5 \times 10^{18}
を 10^9 + 7 で割った余りである 500\,000\,077 を出力します。
入力例 2
1848668
出力例 2
869120830
入力例 3
10000000
出力例 3
787995111
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 1000 点
問題文
数直線上に N 個の星があり、座標の小さい順に 1 から N までの番号が付けられています。星 i \ (1 \leq i \leq N) は座標 X_i にあり、明るさは A_i です。
AtCoder さんは、いくつかの星を写真に撮りたいと思っています。AtCoder さんは、数直線上の区間を好きなように選び、これに含まれる星を撮影します。ここで、写真に写る複数の星が、明るすぎて同一視されることがあります。これは以下の規則に従っています。
- 星 i, j は、\left|X_i - X_j\right| \leq A_i + A_j を満たすとき、同一視される
- 星 i, k が同一視され、星 k, j が同一視されるとき、星 i, j は同一視される
- 以上の規則で同一視されない星は、異なる星として写真に写る
なお、撮影する区間に入らない星は、写真には写らず、同一視の対象にもならないことに注意してください。
さて、撮影する区間をうまく選んだとき、最大でいくつの異なる星として写真に写すことができるでしょうか?
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- T \geq 1
- 1 \leq N \leq 200\,000
- 0 \leq X_1 < \dots < X_N \leq 10^8
- 1 \leq A_i \leq 10^8
- T 個のテストケースにおける N の総和は 200\,000 以下
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられます。ここで \mathrm{case}_i は i 番目のテストケースを意味します。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
各テストケースは以下の形式で与えられます。
N X_1 A_1 X_2 A_2 \vdots X_N A_N
出力
答えを出力してください。
入力例 1
3 4 0 1 3 1 6 5 9 1 6 0 3 1 1 4 1 6 1 9 1 10 3 5 10 5 20 5 30 5 40 5 50 5
出力例 1
2 3 1
1 番目のテストケースにおける写真撮影の方法を 2 通り示します。
- 座標が 0 以上 5 以下の区間を選ぶ場合: 星 1, 2 が写真に写ります。|X_1 - X_2| = 3, A_1 + A_2 = 2 なので、星 1, 2 は別々の星として写真に写ります。
- 座標が 0 以上 9 以下の区間を選ぶ場合: 星 1, 2, 3, 4 が写真に写ります。問題文中の 1 つ目の規則により、星 1, 3、星 2, 3、星 3, 4 が同一視されることになります。それから問題文中の 2 つ目の規則により、星 1, 2, 3, 4 はひとつの星として同一視されます。
このテストケースでは、最大で 2 つの異なる星として写真に写すことができ、そのひとつの方法として 1. の方法が挙げられます。2. の方法では 1 つの星として写真に写るので、最適ではありません。
2 番目のテストケースでは、最大で 3 つの異なる星として写真に写すことができ、そのひとつの方法として座標が 1 以上 9 以下の区間を選ぶ方法が挙げられます。
3 番目のテストケースでは、星を含む区間をどのように選んでも、1 つの星として写真に写ってしまいます。
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1300 点
問題文
N 頂点の木があります。 頂点には 1 から N までの番号が付けられており、i 番目の辺 (1 \leq i \leq N-1) は頂点 u_i と頂点 v_i を結んでいます。 また、各頂点には 1 以上 N 以下の相異なる整数が書かれており、頂点 i (1 \leq i \leq N) に書かれた整数は p_i です。
AtCoder さんは、以下の独立集合シャッフルを高々 5 回行うことができます。
独立集合シャッフルとは
木の各頂点をすべて白で塗った後、以下の 1 と 2 をその順に行う。
- 木のいくつかの頂点を黒で塗る。ただし、辺で隣接する 2 つの頂点の両方を黒で塗ってはならない。
- 黒で塗られた頂点に書かれた整数を並べ替える。
操作の後、少なくとも N-2 個の頂点について、頂点 i (1 \leq i \leq N) に書かれた整数を i にすることができればお金がもらえます。 そのような方法を 1 つ求めてください。 ただし、本問題の制約下では、必ず答えが存在することが証明できます。
制約
- 3 \leq N \leq 150\,000
- 1 \leq u_i < v_i \leq N
- 1 \leq p_i \leq N
- p_1, p_2, \dots, p_N はすべて異なる
- 入力で与えられるグラフは木である
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられます。
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
p_1 p_2 \cdots p_N
出力
以下の形式で答えを出力してください。
ただし、行う独立集合シャッフルの回数を K (\leq 5)、i 回目の独立集合シャッフルの直後に頂点 j に書かれた整数を a_{i,j} とします。 ここで、操作回数を最小化する必要はありません。
K
a_{1,1} a_{1,2} \cdots a_{1,N}
a_{2,1} a_{2,2} \cdots a_{2,N}
\vdots
a_{K,1} a_{K,2} \cdots a_{K,N}
入力例 1
6 1 2 1 3 2 4 2 5 3 6 3 1 5 6 4 2
出力例 1
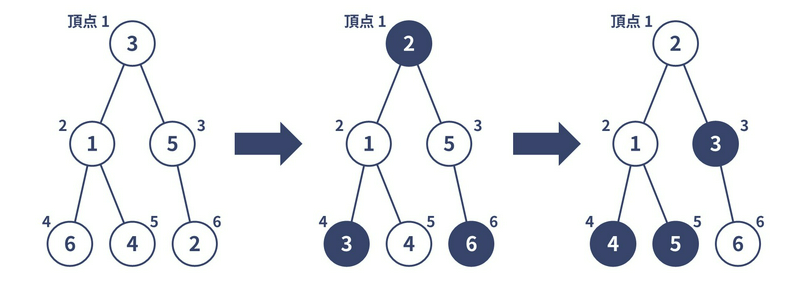
2 2 1 5 3 4 6 2 1 3 4 5 6
たとえば下図のように操作を行うと、5 回以内の独立集合シャッフルで目的を達成することができます。 なお、N 頂点すべてについて頂点 i に書かれた整数を i にする必要はないことに注意してください。
入力例 2
6 1 2 2 3 3 4 4 5 5 6 6 3 5 1 4 2
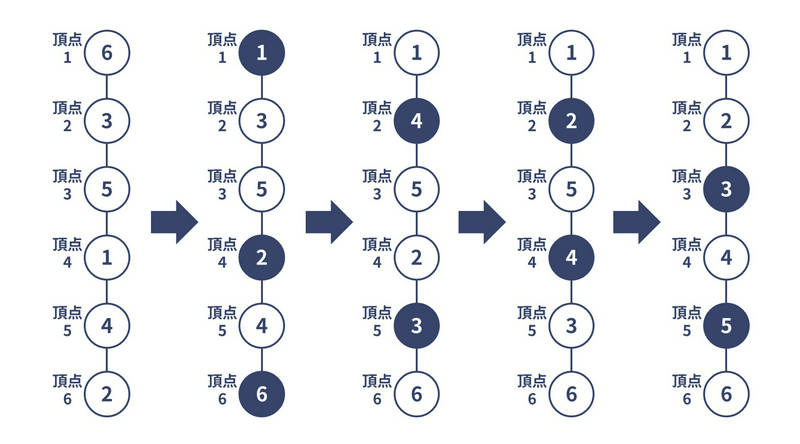
出力例 2
4 1 3 5 2 4 6 1 4 5 2 3 6 1 2 5 4 3 6 1 2 3 4 5 6
たとえば下図のように操作を行うと、5 回以内の独立集合シャッフルで目的を達成することができます。
入力例 3
10 1 2 1 3 2 4 2 5 4 6 3 7 1 8 1 9 2 10 1 2 3 4 5 6 8 7 9 10
出力例 3
0
実行時間制限: 10 sec / メモリ制限: 1024 MiB
配点 : 1300 点
問題文
黒板に N 個の非負整数 A_1,A_2,\cdots,A_N が書かれています。
AtCoder さんはこれから以下の操作を N-1 回行います。
- 黒板に書かれている数を 2 つ選び、消す。選んだ数を x,y として、新たに x \times y+1 を黒板に書き込む。
操作が完了すると、黒板には 1 つの整数が残されることになります。
黒板に書かれている数は値が同じでも互いに区別可能であるとします。 また、2 つの数を選ぶときその順序は区別しません。 つまり、操作を完了する方法は全部で \prod_{2 \leq n \leq N} n \times (n-1) /2 通りあります。
これらすべての方法について、最終的に黒板に残る数を求めたとします。 これらの値の総和を 998\,244\,353 で割ったあまりを求めてください。
制約
- 2 \leq N \leq 250\,000
- 0 \leq A_i < 998\,244\,353
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられます。
N A_1 A_2 \cdots A_N
出力
答えを出力してください。
入力例 1
2 1 2
出力例 1
3
操作を行う方法は 1 通りだけ存在し、最後に残る数は 1 \times 2+1=3 です。
入力例 2
3 1 1 1
出力例 2
9
入力例 3
4 1 2 1 4
出力例 3
276
入力例 4
10 785439575 250040585 709423541 945005786 19237225 404191279 250876592 22672563 519729086 344065186
出力例 4
911129406