Time Limit: 3 sec / Memory Limit: 1024 MiB
ストーリー
たこ焼きが大好きな高橋社長は、たこ焼きを移動させるロボットアームの開発をしている。 二次元グリッドで表現されたたこ焼き器上のいくつかのマスにたこ焼きが置かれている。 ロボットアームを用いて、これらのたこ焼きを指定されたマス集合へ移動させたい。 ロボットアームは複数の指先を持ち、関節と指先を頂点とした木構造で表現される。 一回の操作で、ロボットアーム全体を上下左右に動かす、関節を軸に90度回転させる、指先でたこ焼きを掴む、離す、という操作を同時に行うことが出来る。 操作ターン数が出来るだけ少なくなるようにロボットアームを設計し、操作方法を求めて欲しい。
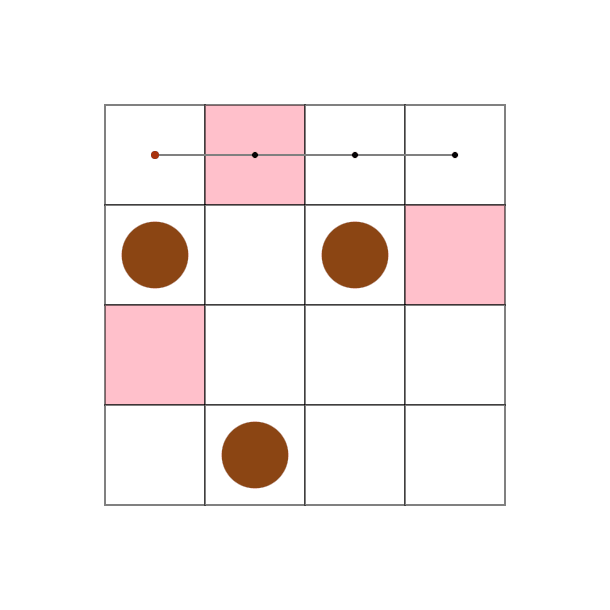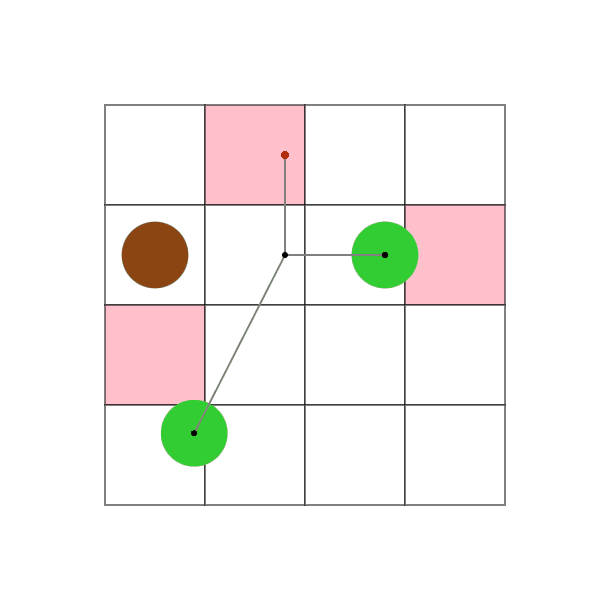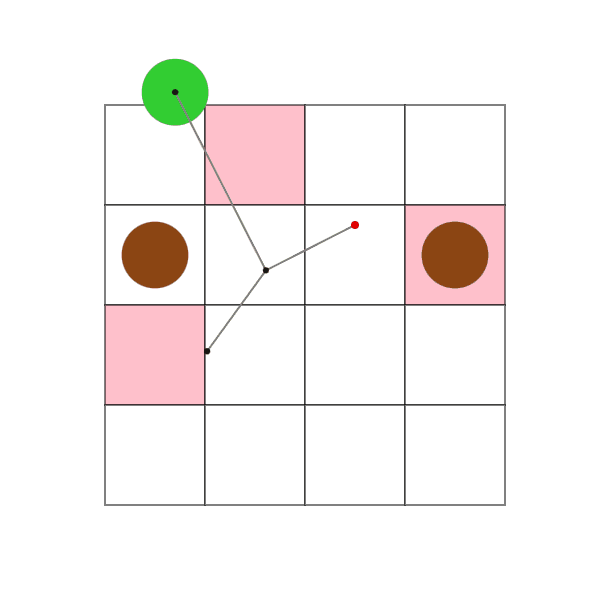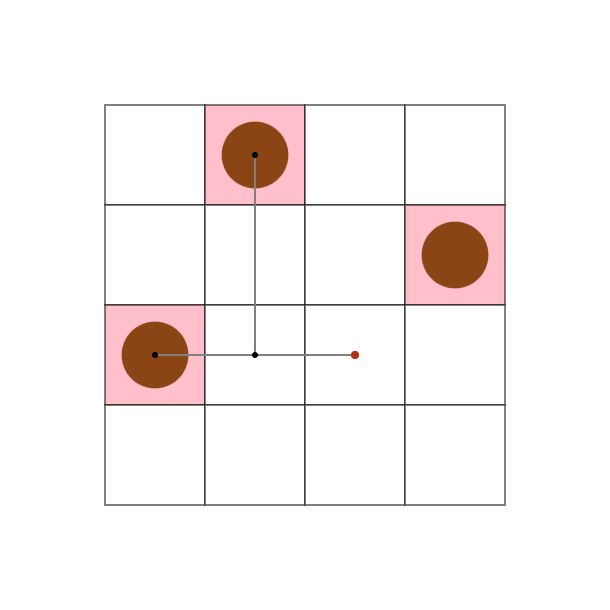
問題文
N\times N マスのたこ焼き器がある。 一番左上のマスの座標を (0,0) とし、そこから下方向に i マス、右方向に j マス進んだ先のマスの座標を (i,j) とする。
初期状態で異なる M マスにたこ焼きが置かれており、 これらを指定された M マスの目的地に移動させたい。
まずはじめに、ロボットアームの設計を行う。 ロボットアームは「関節」と「指先」を頂点とし、その間を剛体の線分で結んだ木構造として表現される。 指先は木の葉に対応し、関節はそれ以外の頂点に対応する。 頂点 u とその子供 v を結ぶ辺の長さを L(u,v) と表記する。
使用可能なロボットアームの頂点数 V が指定されるので、頂点数が V 以下の木を設計し、根の初期位置とともに出力せよ。 木の各辺の長さ L(u,v) は、1\leq L(u,v)\leq N-1 を満たす整数値でなければならない。
次に、設計したロボットアームを操作して、たこ焼きの移動を行う。 指定した初期位置に根があり、全ての辺が右方向に伸びた状態から開始して、毎ターン以下の操作を独立に行うことが出来る。
- ロボットアーム全体を上下左右に1マス動かすことが出来る。移動後の根の座標 (x,y) は 0\leq x,y\leq N-1 を満たす必要がある。
- 根以外の各頂点 u について独立に、u の親 p を軸として u 以下の部分木全体を反時計回りもしくは時計回りに90度回転させることが出来る。
- 各指先について独立に、掴んでいるたこ焼きを現在のマスに置く、もしくは現在のマスに存在するたこ焼きを掴むことが出来る。すでにたこ焼きが置かれているマスや N\times N マスの範囲外にたこ焼きを置くことは出来ない。一つの指先で複数のたこ焼きを同時に掴むことも出来ない。
操作2の例
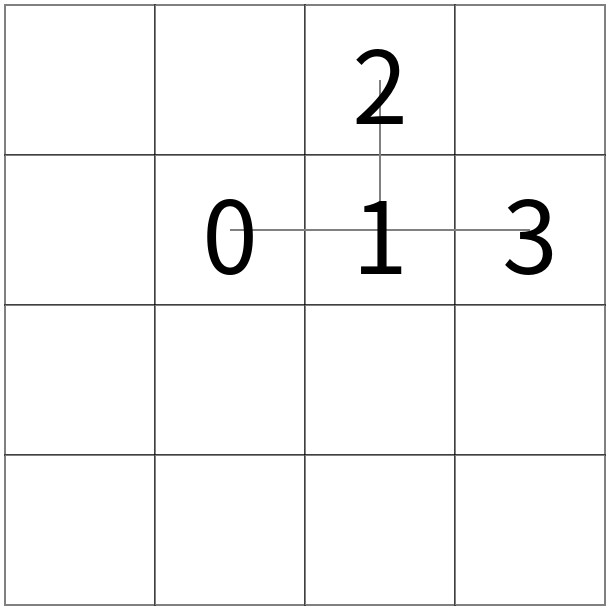 ➡
➡
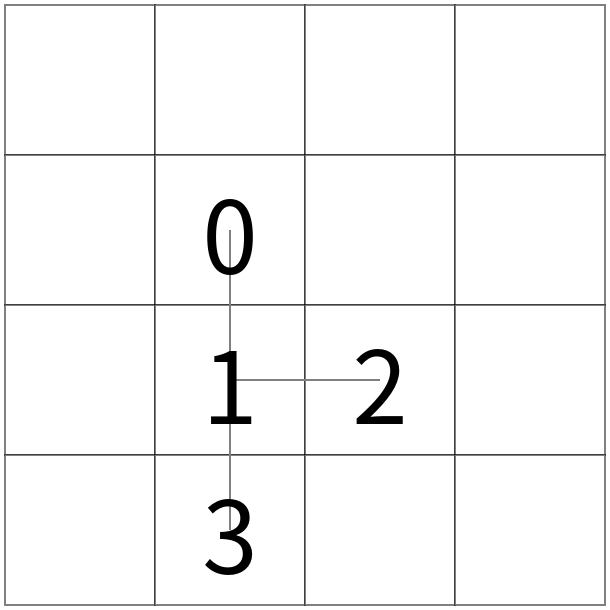 ➡
➡
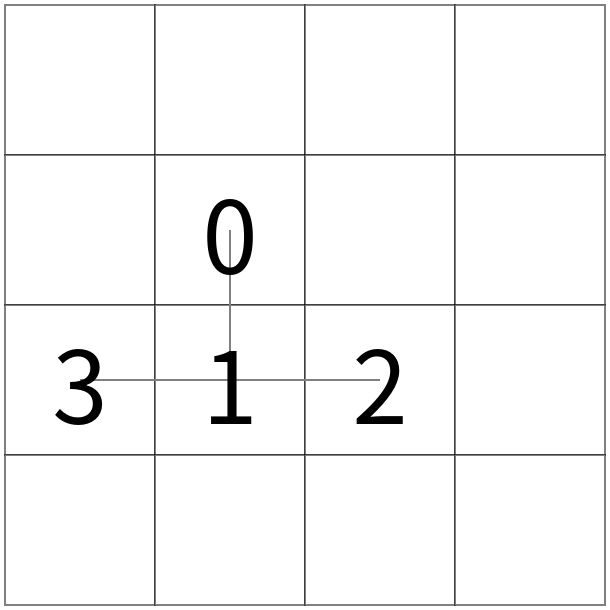
左図から、頂点 0 を軸として 1 以下の部分木全体を時計回りに回転させると真ん中の図の状態となる。 更に、頂点 1 を軸として 3 以下の部分木全体を時計回りに回転させると右図の状態となる。
操作は 1 と 2 の後に 3 の順で行われ、操作 3 の中では頂点番号の小さい指先から順に処理が行われる (1、2 内の順番は操作後の状態に影響を与えない)。 操作後にロボットアームの一部が N\times N マスの外部にはみ出しても良く、ロボットアームの複数の頂点が同じマスを共有しても良い。
操作は最大で 10^5 ターン行うことが出来る。
得点
操作ターン数を K、操作終了時に目的地に存在するたこ焼きの個数を M' とする。 このとき、以下の絶対スコアが得られる。 絶対スコアは小さければ小さいほど良い。
- M'=M の場合、K
- M'<M の場合、10^5+1000\times (M-M')
各テストケース毎に、\mathrm{round}(10^9\times \frac{全参加者中の最小絶対スコア}{自身の絶対スコア}) の相対評価スコアが得られ、その和が提出の得点となる。
最終順位はコンテスト終了後に実施されるより多くの入力に対するシステムテストにおける得点で決定される。 暫定テスト、システムテストともに、一部のテストケースで不正な出力や制限時間超過をした場合、そのテストケースの相対評価スコアは0点となり、そのテストケースにおいては「全参加者中の最小絶対スコア」の計算から除外される。 システムテストは CE 以外の結 果を得た一番最後の提出に対してのみ行われるため、最終的に提出する解答を間違えないよう注意せよ。
テストケース数
- 暫定テスト: 50個
- システムテスト: 2000個、コンテスト終了後に seeds.txt (sha256=c5e999464ec12906e690f995b8d1db2a03a87eec65faff2cecf01263dd035c68) を公開
相対評価システムについて
暫定テスト、システムテストともに、CE 以外の結果を得た一番最後の提出のみが順位表に反映される。 相対評価スコアの計算に用いられる各テストケース毎の全参加者中の最小絶対スコアの算出においても、順位表に反映されている最終提出のみが用いられる。
順位表に表示されているスコアは相対評価スコアであり、新規提出があるたびに、相対評価スコアが再計算される。 一方、提出一覧から確認出来る各提出のスコアは各テストケース毎の絶対スコアをそのまま足し合わせたものであり、相対評価スコアは表示されない。 最新以外の提出の、現在の順位表における相対評価スコアを知るためには、再提出が必要である。 不正な出力や制限時間超過をした場合、提出一覧から確認出来るスコアは0となるが、順位表には正解したテストケースに対する相対スコアの和が表示されている。
実行時間について
実行時間には多少のブレが生じます。 また、システムテストでは同時に大量の実行を行うため、暫定テストに比べて数%程度実行時間が伸びる現象が確認されています。 そのため、実行時間制限ギリギリの提出がシステムテストでTLEとなる可能性がありま す。 プログラム内で時間を計測して処理を打ち切るか、実行時間に余裕を持たせるようお願いします。
入力
入力は以下の形式で標準入力から与えられる。
N M V
s_{0,0}\cdots s_{0,N-1}
\vdots
s_{N-1,0}\cdots s_{N-1,N-1}
t_{0,0}\cdots t_{0,N-1}
\vdots
t_{N-1,0}\cdots t_{N-1,N-1}
- グリッドの大きさ N は 15\leq N\leq 30 を満たす整数値である。
- たこ焼きの個数 M は N^2/10\leq M\leq N^2/2 を満たす整数値である。
- 使用可能なロボットアームの頂点数 V は 5\leq V\leq 15 を満たす整数値である。
- s_{i,0}\cdots s_{i,N-1} は
01からなる N 文字の文字列であり、その j 文字目が1の場合、初期状態でマス (i,j) にたこ焼きが置かれていることを表す。たこ焼きが置かれているマスの個数はちょうど M である。 - t_{i,0}\cdots t_{i,N-1} は
01からなる N 文字の文字列であり、その j 文字目が1の場合、マス (i,j) は目的地であることを表す。目的地であるマスの個数はちょうど M である。
出力
設計したロボットアームの頂点数を V'(1\leq V'\leq V) とする。 頂点 0 を根とし、頂点 u の親は u 未満となるよう、ロボットアームの各頂点に 0,\cdots,V'-1 の番号を振る。 頂点 u (1\leq u\leq V'-1) の親を p_u (0\leq p_u\leq u-1) とし、辺 (p_u,u) の長さを L(p_u,u) (1\leq L(p_u,u)\leq N-1) とする。 初期状態における根の座標を (x,y) (0\leq x,y\leq N-1) とする。 このとき、以下の形式で標準出力に出力せよ。
V'
p_1 L(p_1,1)
\vdots
p_{V'-1} L(p_{V'-1},V'-1)
x y
次に、操作列を出力する。 1ターンの操作を以下のようにして 2V' 文字の文字列 S で表現する。
- 0 文字目は、ロボットアーム全体を上下左右に1マス動かすならばそれぞれ、
U、D、L、Rであり、動かさないならば.である。 - i 文字目 (1\leq i\leq V'-1) は、p_i を軸として頂点 i 以下の部分木全体を反時計回りに 90 度回転させるならば
L、時計回りに 90 度回転させるならばR、何もしないならば.である。 - (V'+i) 文字目 (0\leq i\leq V'-1) は、頂点 i が指先(葉)でないもしくは何もしないならば
.、たこ焼きを掴むもしくは離すならばPである。
操作列の長さを T、t ターン目の操作列を表す文字列を S_t としたとき、以下の形式で標準出力に出力せよ。
S_0
\vdots
S_{T-1}
サンプルプログラム(Python)
import random
random.seed(42)
DX = [0, 1, 0, -1]
DY = [1, 0, -1, 0]
DIR = ['R', 'D', 'L', 'U']
# read input
N, M, V = map(int, input().split())
s = [list(map(int, list(input()))) for _ in range(N)]
t = [list(map(int, list(input()))) for _ in range(N)]
# design the tree
tree = [[0, 1]]
print(len(tree) + 1)
for p, L in tree:
print(p, L)
# decide the initial position
rx, ry = 0, 0
print(rx, ry)
dir1 = 0 # direction of edge (0, 1)
holding = False # whether holding a takoyaki
for turn in range(100):
S = []
# random move
dir = random.randint(0, 3)
dx, dy = DX[dir], DY[dir]
if 0 <= rx + dx < N and 0 <= ry + dy < N:
rx += dx
ry += dy
S.append(DIR[dir])
else:
S.append('.')
# random rotate
rot = random.randint(0, 2)
if rot == 0:
S.append('.')
elif rot == 1:
S.append('L')
dir1 = (dir1 + 3) % 4
else:
S.append('R')
dir1 = (dir1 + 1) % 4
# grab or release takoyaki
x, y = rx + DX[dir1], ry + DY[dir1]
change = False
if 0 <= x and x < N and 0 <= y and y < N:
if s[x][y] == 1 and t[x][y] == 0 and not holding:
change = True
s[x][y] = 0
holding = True
elif s[x][y] == 0 and t[x][y] == 1 and holding:
change = True
s[x][y] = 1
holding = False
S.append('.') # vertex 0 (root) is not a leaf
if change:
S.append('P')
else:
S.append('.')
# output the command
print(''.join(S))
入力生成方法
L 以上 U 以下の整数値を一様ランダムに生成する関数を \mathrm{rand}(L,U)、 L 以上 U 以下の浮動小数値を一様ランダムに生成する関数を \mathrm{rand\_double}(L,U) で表す。
N, M, V は指定された範囲の整数から一様ランダムに生成される。 たこ焼きの初期位置は以下のようにして生成される。
まず、N\times N の重み配列 w を 0 で初期化する。 以下の処理を \mathrm{rand}(1, 5) 回繰り返す。
- 中心 (cx,cy) を cx=\mathrm{rand\_double}(-1,N), cy=\mathrm{rand\_double}(-1,N) により生成
- 係数 a を a=\mathrm{rand\_double}(0,1) により生成
- \sigma を \sigma=\mathrm{rand\_double}(2,5) により生成
- 各マス (i,j) について、w_{i,j} に a\exp(-((i-cx)^2+(j-cy)^2)/(2\sigma^2)) を加算
得られた重み w_{i,j} に比例する確率で M 個のマスを非復元抽出し、たこ焼きの初期位置とする。
たこ焼きの目的地も同じ方法で生成する。 初期位置に含まれるが目的地に含まれない、もしくは初期位置に含まれないが目的地に含まれるマスの個数を数え、それが M 未満であれば、初期位置と目的地の生成をやり直す。
ツール(入力ジェネレータ・ビジュアライザ)
- Web版: ローカル版より高性能でアニメーション表示が可能です。
- ローカル版: 使用するにはRust言語のコンパイル環境をご用意下さい。
- Windows用のコンパイル済みバイナリ: Rust言語の環境構築が面倒な方は代わりにこちらをご利用下さい。
コンテスト期間中に、ビジュアライズ結果の共有や、解法・考察に関する言及は禁止されています。ご注意下さい。
入力例 1
4 3 4 0000 1010 0000 0100 0100 0001 1000 0000
出力例 1
4 0 1 1 1 1 2 0 0 RRL...PP R..R..P. DRR...P. D.....PP
問題文の先頭で図示した入出力例となります。 この例は、入力の制約は満たしていません。
Story
CEO Takahashi, who loves takoyaki (japanese food), is developing a robotic arm to assist in moving takoyaki on a takoyaki cooker. On the takoyaki cooker represented by a 2D grid, several takoyaki are placed on some of the grid squares. Using a robotic arm, you need to move the takoyaki from these squares to a specified set of target squares. The robotic arm has multiple fingertips and is structured as a tree, with joints and fingertips as its vertices. In a single turn, the robotic arm can simultaneously perform the following actions: move the entire arm up, down, left, or right; rotate around a joint by 90 degrees; grab or release takoyaki with its fingertips. Design the robotic arm and determine the operation method to reduce the number of turns as much as possible.

Problem Statement
There is an N \times N takoyaki cooker. Let (0,0) be the coordinates of the top-left square and (i,j) be the coordinates of the square located i squares down and j squares to the right from there.
Initially, takoyaki are placed on M different squares, and you need to move them to M specified target squares.
First, you must design the robotic arm.
The robotic arm is represented as a tree where the "joints" and "fingertips" are the vertices, and the rigid segments connecting them are the edges.
The fingertips correspond to the leaves of the tree, while the joints correspond to the other vertices.
The length of the edge connecting vertex u and its child v is denoted as L(u,v).
You are given the number of vertices V available for the robotic arm, and your task is to design a tree with no more than V vertices and output it along with the initial position of the root. The length of each edge L(u,v) must be an integer satisfying 1 \leq L(u,v) \leq N-1.
Next, you must operate the designed robotic arm to move the takoyaki. Starting from the initial position where the root is at the specified position and all edges extend to the right, you can perform the following operations independently each turn:
- You can move the entire robotic arm one square up, down, left, or right. The new coordinates of the root (x,y) must satisfy 0 \leq x, y \leq N-1.
- For each vertex u other than the root, you can independently rotate the entire subtree rooted at u by 90 degrees either counterclockwise or clockwise around its parent p.
- For each fingertip, you can independently place the takoyaki it is holding on the current square, or pick up a takoyaki from the current square. You cannot place a takoyaki on a square that already contains one or outside the N \times N grid. Each fingertip cannot hold more than one takoyaki at the same time.
Example of Operation 2
 ➡
➡
 ➡
➡

Starting from the left figure, rotating the entire subtree rooted at vertex 1 by 90 degrees clockwise around vertex 0 results in the middle figure.
Furthermore, rotating the entire subtree rooted at vertex 3 by 90 degrees clockwise around vertex 1 results in the right figure.
Operations are performed in the order of 1 and 2 first, followed by 3. In operation 3, the fingertips are processed in order from the smallest vertex number to the largest (the order within 1 and 2 does not affect the result). It is allowed for part of the robotic arm to extend outside the N \times N grid after an operation, and multiple vertices of the robotic arm can occupy the same square.
You can perform up to 10^5 turns.
Scoring
Let K be the number of turns, and let M' be the number of takoyaki at the target positions at the end of the operations.
Then, you will obtain the following absolute score.
The lower the absolute score, the better.
- If M'=M, K
- If M'<M, 10^5+1000\times (M-M')
For each test case, we compute the relative score \mathrm{round}(10^9\times \frac{\mathrm{MIN}}{\mathrm{YOUR}}), where YOUR is your absolute score and MIN is the lowest absolute score among all competitors obtained on that test case. The score of the submission is the sum of the relative scores.
The final ranking will be determined by the system test with more inputs which will be run after the contest is over. In both the provisional/system test, if your submission produces illegal output or exceeds the time limit for some test cases, only the score for those test cases will be zero, and your submission will be excluded from the MIN calculation for those test cases.
The system test will be performed only for the last submission which received a result other than CE . Be careful not to make a mistake in the final submission.
Number of test cases
- Provisional test: 50
- System test: 2000. We will publish seeds.txt (sha256=c5e999464ec12906e690f995b8d1db2a03a87eec65faff2cecf01263dd035c68) after the contest is over.
About relative evaluation system
In both the provisional/system test, the standings will be calculated using only the last submission which received a result other than CE. Only the last submissions are used to calculate the MIN for each test case when calculating the relative scores.
The scores shown in the standings are relative, and whenever a new submission arrives, all relative scores are recalculated. On the other hand, the score for each submission shown on the submissions page is the sum of the absolute score for each test case, and the relative scores are not shown. In order to know the relative score of submission other than the latest one in the current standings, you need to resubmit it. If your submission produces illegal output or exceeds the time limit for some test cases, the score shown on the submissions page will be 0, but the standings show the sum of the relative scores for the test cases that were answered correctly.
About execution time
Execution time may vary slightly from run to run. In addition, since system tests simultaneously perform a large number of executions, it has been observed that execution time increases by several percent compared to provisional tests. For these reasons, submissions that are very close to the time limit may result in TLE in the system test. Please measure the execution time in your program to terminate the process, or have enough margin in the execution time.
Input
Input is given from Standard Input in the following format.
N M V
s_{0,0}\cdots s_{0,N-1}
\vdots
s_{N-1,0}\cdots s_{N-1,N-1}
t_{0,0}\cdots t_{0,N-1}
\vdots
t_{N-1,0}\cdots t_{N-1,N-1}
- The size of the grid N is an integer that satisfies 15 \leq N \leq 30.
- The number of takoyaki M is an integer that satisfies N^2/10 \leq M \leq N^2/2.
- The number of vertices V available for the robotic arm is an integer that satisfies 5 \leq V \leq 15.
- s_{i,0} \cdots s_{i,N-1} is a string of length N consisting of
01. If the j-th character is1, it means that a takoyaki is initially placed on square (i,j). The total number of squares with takoyaki is exactly M. - t_{i,0} \cdots t_{i,N-1} is a string of length N consisting of
01. If the j-th character is1, it means that square (i,j) is a target position. The total number of target squares is exactly M.
Output
Let V' be the number of vertices in the designed robotic arm, where 1 \leq V' \leq V.
The vertices of the robotic arm are numbered from 0 to V'-1 such that vertex 0 is the root, and the parent of vertex u is a vertex with a number smaller than u.
Let p_u (0 \leq p_u \leq u-1) be the parent of vertex u (1 \leq u \leq V'-1), and let the length of the edge (p_u, u) be L(p_u, u), where 1 \leq L(p_u, u) \leq N-1.
Let the coordinates of the root in the initial state be (x, y), where 0 \leq x, y \leq N-1.
Then, output to Standard Output in the following format.
V'
p_1 L(p_1, 1)
\vdots
p_{V'-1} L(p_{V'-1}, V'-1)
x y
Next, output the sequence of operations.
Each turn's operation is represented by a string S of length 2V' as follows:
- The 0-th character represents the movement of the entire robotic arm by one square up (
U), down (D), left (L), right (R), or no movement (.). - The i-th character (1 \leq i \leq V'-1) represents the rotation of the entire subtree rooted at vertex i around p_i: counterclockwise by 90 degrees is represented by
L, clockwise by 90 degrees is represented byR, and no rotation is represented by.. - The (V' + i)-th character (0 \leq i \leq V'-1) represents the action of vertex i. If the vertex is not a fingertip (leaf) or no action is taken, it is represented by a
.. If the fingertip grabs or releases a takoyaki, it is represented byP.
Let T be the number of turns, and let S_t represent the string for the t-th turn. Output to Standard Output in the following format.
S_0
\vdots
S_{T-1}
Sample Solution(Python)
import random
random.seed(42)
DX = [0, 1, 0, -1]
DY = [1, 0, -1, 0]
DIR = ['R', 'D', 'L', 'U']
# read input
N, M, V = map(int, input().split())
s = [list(map(int, list(input()))) for _ in range(N)]
t = [list(map(int, list(input()))) for _ in range(N)]
# design the tree
tree = [[0, 1]]
print(len(tree) + 1)
for p, L in tree:
print(p, L)
# decide the initial position
rx, ry = 0, 0
print(rx, ry)
dir1 = 0 # direction of edge (0, 1)
holding = False # whether holding a takoyaki
for turn in range(100):
S = []
# random move
dir = random.randint(0, 3)
dx, dy = DX[dir], DY[dir]
if 0 <= rx + dx < N and 0 <= ry + dy < N:
rx += dx
ry += dy
S.append(DIR[dir])
else:
S.append('.')
# random rotate
rot = random.randint(0, 2)
if rot == 0:
S.append('.')
elif rot == 1:
S.append('L')
dir1 = (dir1 + 3) % 4
else:
S.append('R')
dir1 = (dir1 + 1) % 4
# grab or release takoyaki
x, y = rx + DX[dir1], ry + DY[dir1]
change = False
if 0 <= x and x < N and 0 <= y and y < N:
if s[x][y] == 1 and t[x][y] == 0 and not holding:
change = True
s[x][y] = 0
holding = True
elif s[x][y] == 0 and t[x][y] == 1 and holding:
change = True
s[x][y] = 1
holding = False
S.append('.') # vertex 0 (root) is not a leaf
if change:
S.append('P')
else:
S.append('.')
# output the command
print(''.join(S))
Input Generation
Let \mathrm{rand}(L,U) be a function that generates a uniform random integer between L and U, inclusive. Let \mathrm{rand\_double}(L,U) be a function that generates a uniform random floating-point number between L and U, inclusive.
The values of N, M, and V are uniformly generated as random integers within the specified ranges.
The initial positions of the takoyaki are generated as follows:
First, initialize the weight array w of size N \times N with zeros.
Repeat the following process \mathrm{rand}(1, 5) times:
- Generate a center (cx, cy) where cx = \mathrm{rand\_double}(-1, N) and cy = \mathrm{rand\_double}(-1, N).
- Generate a coefficient a where a = \mathrm{rand\_double}(0, 1).
- Generate \sigma where \sigma = \mathrm{rand\_double}(2, 5).
- For each square (i, j), add a \exp(-((i - cx)^2 + (j - cy)^2) / (2 \sigma^2)) to w_{i,j}.
Then, using probabilities proportional to the obtained weights w_{i,j}, extract M squares without replacement to determine the initial positions of the takoyaki.
The target positions for the takoyaki are generated in the same way.
If the number of squares that are included in the initial positions but not in the target positions, or vice versa, is less than M, redo the generation of both the initial positions and the target positions.
Tools (Input generator and visualizer)
- Web version: This is more powerful than the local version providing animations.
- Local version: You need a compilation environment of Rust language.
- Pre-compiled binary for Windows: If you are not familiar with the Rust language environment, please use this instead.
Please be aware that sharing visualization results or discussing solutions/ideas during the contest is prohibited.
Sample Input 1
4 3 4 0000 1010 0000 0100 0100 0001 1000 0000
Sample Output 1
4 0 1 1 1 1 2 0 0 RRL...PP R..R..P. DRR...P. D.....PP
This is an example of input and output, visualized at the beginning of the problem statement. This example does not satisfy the input constraints.
Time Limit: 0 msec / Memory Limit: 1024 MiB