Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 300 点
問題文
2N 人の卓球選手が、1 から N までの番号がついた N 台の卓で実戦練習を行います。
練習は複数の ラウンド からなります。 各ラウンドでは、選手たちは 1 卓につき 1 ペアの合計 N ペアに分かれます。 そして、各ペアの選手同士で試合を行い、1 人が勝利してもう 1 人が敗北します。
卓 X で勝利した選手は、次のラウンドでは卓 X-1 で試合を行います。 ただし、卓 1 で勝利した選手は卓 1 に留まります。
同様に、卓 X で敗北した選手は、次のラウンドでは卓 X+1 で試合を行います。 ただし、卓 N で敗北した選手は卓 N に留まります。
ある 2 人の選手は友達同士で、最初のラウンドの試合を異なる卓 A, B で行います。 彼らは十分な腕前を持ち、各試合での自分の勝敗を自由に操れるとします。 この 2 人同士で試合を行えるまでに、最小で何回のラウンドが必要でしょうか?
制約
- 2 \leq N \leq 10^{18}
- 1 \leq A < B \leq N
- 入力中のすべての値は整数である。
入力
入力は以下の形式で標準入力から与えられる。
N A B
出力
友達の 2 人同士で試合を行えるまでに必要な最小のラウンド数を出力せよ。
入力例 1
5 2 4
出力例 1
1
最初のラウンドで 1 人目が敗北して 2 人目が勝利すると、2 人とも卓 3 に移動し、次のラウンドでは彼ら同士で試合を行えます。
入力例 2
5 2 3
出力例 2
2
2 人とも 2 連続で勝利すれば、両者とも卓 1 に移れます。
Score : 300 points
Problem Statement
2N players are running a competitive table tennis training on N tables numbered from 1 to N.
The training consists of rounds. In each round, the players form N pairs, one pair per table. In each pair, competitors play a match against each other. As a result, one of them wins and the other one loses.
The winner of the match on table X plays on table X-1 in the next round, except for the winner of the match on table 1 who stays at table 1.
Similarly, the loser of the match on table X plays on table X+1 in the next round, except for the loser of the match on table N who stays at table N.
Two friends are playing their first round matches on distinct tables A and B. Let's assume that the friends are strong enough to win or lose any match at will. What is the smallest number of rounds after which the friends can get to play a match against each other?
Constraints
- 2 \leq N \leq 10^{18}
- 1 \leq A < B \leq N
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N A B
Output
Print the smallest number of rounds after which the friends can get to play a match against each other.
Sample Input 1
5 2 4
Sample Output 1
1
If the first friend loses their match and the second friend wins their match, they will both move to table 3 and play each other in the next round.
Sample Input 2
5 2 3
Sample Output 2
2
If both friends win two matches in a row, they will both move to table 1.
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 700 点
問題文
あるコンテストの開催に向けて N 問の問題が提案されました。はじめ、問題 i のスコアは整数 A_i です。
これから、M 人のジャッジが好きな問題に投票します。各ジャッジは、他のジャッジとは独立にちょうど V 問を選び、それらの問題のスコアを 1 ずつ上げます。
M 人のジャッジ全員が投票を行ったあと、N 問の問題がスコアの降順に並べられ、最初の P 問がコンテストの問題セットに採用されます。 同スコアの問題間の順序は、ジャッジ長が任意に決定します。
N 問のうち、問題セットに採用される可能性を持つ問題は何問あるでしょうか?
制約
- 2 \le N \le 10^5
- 1 \le M \le 10^9
- 1 \le V \le N - 1
- 1 \le P \le N - 1
- 0 \le A_i \le 10^9
入力
入力は以下の形式で標準入力から与えられる。
N M V P A_1 A_2 ... A_N
出力
問題セットに採用される可能性を持つ問題の数を出力せよ。
入力例 1
6 1 2 2 2 1 1 3 0 2
出力例 1
5
1 人しかいないジャッジが問題 2,5 に投票した場合、各問のスコアは 2 2 1 3 1 2 となり、問題 4、そして問題 1,2,6 のうちの 1 問が採用されます。
ジャッジが問題 3,4 に投票した場合、各問のスコアは 2 1 2 4 0 2 となり、問題 4、そして問題 1,3,6 のうちの 1 問が採用されます。
よって、問題 1,2,3,4,6 には採用される可能性があります。一方で、問題 5 には採用される可能性はありません。
入力例 2
6 1 5 2 2 1 1 3 0 2
出力例 2
3
採用される可能性があるのは問題 1,4,6 のみです。
入力例 3
10 4 8 5 7 2 3 6 1 6 5 4 6 5
出力例 3
8
Score : 700 points
Problem Statement
N problems are proposed for an upcoming contest. Problem i has an initial integer score of A_i points.
M judges are about to vote for problems they like. Each judge will choose exactly V problems, independently from the other judges, and increase the score of each chosen problem by 1.
After all M judges cast their vote, the problems will be sorted in non-increasing order of score, and the first P problems will be chosen for the problemset. Problems with the same score can be ordered arbitrarily, this order is decided by the chief judge.
How many problems out of the given N have a chance to be chosen for the problemset?
Constraints
- 2 \le N \le 10^5
- 1 \le M \le 10^9
- 1 \le V \le N - 1
- 1 \le P \le N - 1
- 0 \le A_i \le 10^9
Input
Input is given from Standard Input in the following format:
N M V P A_1 A_2 ... A_N
Output
Print the number of problems that have a chance to be chosen for the problemset.
Sample Input 1
6 1 2 2 2 1 1 3 0 2
Sample Output 1
5
If the only judge votes for problems 2 and 5, the scores will be 2 2 1 3 1 2. The problemset will consist of problem 4 and one of problems 1, 2, or 6.
If the only judge votes for problems 3 and 4, the scores will be 2 1 2 4 0 2. The problemset will consist of problem 4 and one of problems 1, 3, or 6.
Thus, problems 1, 2, 3, 4, and 6 have a chance to be chosen for the problemset. On the contrary, there is no way for problem 5 to be chosen.
Sample Input 2
6 1 5 2 2 1 1 3 0 2
Sample Output 2
3
Only problems 1, 4, and 6 have a chance to be chosen.
Sample Input 3
10 4 8 5 7 2 3 6 1 6 5 4 6 5
Sample Output 3
8
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 900 点
問題文
N 行 N 列のマスからなる盤面を考えます。あなたはこの上にドミノ牌を何枚か置こうとしています。 各牌は一辺を共有する 2 マスの上に置き、各マスに乗せられる牌は 1 枚までです。
盤面の各行について、その行の 1 マス以上を占める牌の数をその行のクオリティと定義します。 各列のクオリティも同様に定義します。
1 枚以上の牌の盤面への置き方であって、どの行のクオリティもどの列のクオリティとも等しくなるものを求めてください。あるいは、そのような置き方が存在しないことを検出してください。
制約
- 2 \le N \le 1000
入力
入力は以下の形式で標準入力から与えられる。
N
出力
題意を満たす牌の置き方が存在しない場合、整数 -1 のみを出力せよ。
そうでなければ、題意を満たす牌の置き方をそれぞれ長さ N の文字列 N 個として出力せよ。
牌が乗せられていないマスに対応する文字は . (ドット) とし、牌が乗せられているマスに対応する文字は英小文字とすること。
同一の牌が占めるマスには同一の文字を用い、一辺を共有する 2 マスが異なる牌に占められている場合、それらのマスには異なる文字を用いよ。
入力例 1
6
出力例 1
aabb.. b..zz. ba.... .a..aa ..a..b ..a..b
どの行のクオリティも、どの列のクオリティも 2 です。
入力例 2
2
出力例 2
-1
Score : 900 points
Problem Statement
Let us consider a grid of squares with N rows and N columns. You want to put some domino pieces on this grid. Each domino piece covers two squares that have a common side. Each square can be covered by at most one piece.
For each row of the grid, let's define its quality as the number of domino pieces that cover at least one square in this row. We define the quality of each column similarly.
Find a way to put at least one domino piece on the grid so that the quality of every row is equal to the quality of every column, or determine that such a placement doesn't exist.
Constraints
- 2 \le N \le 1000
Input
Input is given from Standard Input in the following format:
N
Output
If the required domino placement doesn't exist, print a single integer -1.
Otherwise, output your placement as N strings of N characters each.
If a square is not covered, the corresponding character must be . (a dot).
Otherwise, it must contain a lowercase English letter.
Squares covered by the same domino piece must contain the same letter.
If two squares have a common side but belong to different pieces, they must contain different letters.
Sample Input 1
6
Sample Output 1
aabb.. b..zz. ba.... .a..aa ..a..b ..a..b
The quality of every row and every column is 2.
Sample Input 2
2
Sample Output 2
-1
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 1200 点
問題文
コンテストで使う N 問の問題がジャッジに選ばれ、各問に配点を付ける段階になりました。
問題 i の配点 A_i は、1 以上 N 以下の整数でなければなりません。 また、すでに問題は難易度順に並んでおり、A_1 \le A_2 \le \ldots \le A_N でなければなりません (複数問の配点が同じになるのは構いませんが)。
ICPC のファンであるあなたは、解いた問題数が多い参加者ほど上位となってほしいと考えています。 この理由から、任意の k (1 \le k \le N-1) に対して、任意の k 問の配点の合計が任意の k+1 問の配点の合計より真に小さくなるようにしたい、とあなたは考えています。
このような配点の付け方は何通りあるでしょうか?この数を与えられた素数 M で割った余りを求めてください。
制約
- 2 \leq N \leq 5000
- 9 \times 10^8 < M < 10^9
- M は素数である。
- 入力中のすべての値は整数である。
入力
入力は以下の形式で標準入力から与えられる。
N M
出力
配点の付け方の数を M で割った余りを出力せよ。
入力例 1
2 998244353
出力例 1
3
可能な配点の付け方は (1, 1), (1, 2), (2, 2) です。
入力例 2
3 998244353
出力例 2
7
可能な配点の付け方は (1, 1, 1), (1, 2, 2), (1, 3, 3), (2, 2, 2), (2, 2, 3), (2, 3, 3), (3, 3, 3) です。
入力例 3
6 966666661
出力例 3
66
入力例 4
96 925309799
出力例 4
83779
Score : 1200 points
Problem Statement
N problems have been chosen by the judges, now it's time to assign scores to them!
Problem i must get an integer score A_i between 1 and N, inclusive. The problems have already been sorted by difficulty: A_1 \le A_2 \le \ldots \le A_N must hold. Different problems can have the same score, though.
Being an ICPC fan, you want contestants who solve more problems to be ranked higher. That's why, for any k (1 \le k \le N-1), you want the sum of scores of any k problems to be strictly less than the sum of scores of any k+1 problems.
How many ways to assign scores do you have? Find this number modulo the given prime M.
Constraints
- 2 \leq N \leq 5000
- 9 \times 10^8 < M < 10^9
- M is a prime.
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N M
Output
Print the number of ways to assign scores to the problems, modulo M.
Sample Input 1
2 998244353
Sample Output 1
3
The possible assignments are (1, 1), (1, 2), (2, 2).
Sample Input 2
3 998244353
Sample Output 2
7
The possible assignments are (1, 1, 1), (1, 2, 2), (1, 3, 3), (2, 2, 2), (2, 2, 3), (2, 3, 3), (3, 3, 3).
Sample Input 3
6 966666661
Sample Output 3
66
Sample Input 4
96 925309799
Sample Output 4
83779
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 1600 点
問題文
平衡ネットワーク とは、左から右へと延びる N 本のケーブルと、それぞれ 2 本のケーブルを繋ぐ M 個の 平衡器 からなる抽象機械です。 ケーブルには上から順に 1 から N までの番号が、平衡器には左から順に 1 から M までの番号がついています。平衡器 i はケーブル x_i, y_i (x_i < y_i) を繋ぎます。
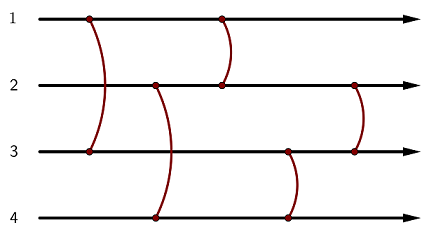
各平衡器は 上 または 下 のいずれかの状態に設定します。
1 枚のコインが、いずれかのケーブルに沿ってどの平衡器よりも左に位置する点から右へと流れ始めるとします。 これから、このコインはすべての平衡器のもとをちょうど一度ずつ通過します。 コインが平衡器 i の位置に来たとき、次のことが起こります。
- コインがケーブル x_i に沿って流れており、かつ平衡器 i の状態が下であるなら、コインはケーブル y_i に移ってから再び右へと流れる。
- コインがケーブル y_i に沿って流れており、かつ平衡器 i の状態が上であるなら、コインはケーブル x_i に移ってから再び右へと流れる。
- 上記のいずれでもないなら、コインが別のケーブルに移ることはない。
平衡ネットワークの状態とは、すべての平衡器の状態を表す長さ M の文字列です。
この文字列の i 文字目は、平衡器 i の状態が上なら ^、下なら v です。
平衡ネットワークの状態が 均一的 であるとは、あるケーブル w が存在して、コインがどのケーブルから流れ始めたとしてもケーブル w に行き着き、これに沿って永遠に流れることをいいます。それ以外の場合、平衡ネットワークの状態は 非均一的 であるといわれます。
整数 T (1 \le T \le 2) が与えられます。次の問いに答えてください。
- T = 1 の場合は、このネットワークの均一的な状態をいずれかひとつ求めるか、そのような状態が存在しないことを検出せよ。
- T = 2 の場合は、このネットワークの非均一的な状態をいずれかひとつ求めるか、そのような状態が存在しないことを検出せよ。
なお、いずれか 1 種類の問いにのみ正しく答えると部分点が得られます。
制約
- 2 \leq N \leq 50000
- 1 \leq M \leq 100000
- 1 \leq T \leq 2
- 1 \leq x_i < y_i \leq N
- 入力中のすべての値は整数である。
部分点
- T = 1 であるようなテストケースすべてに正解すると、800 点が与えられる。
- T = 2 であるようなテストケースすべてに正解すると、800 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N M T x_1 y_1 x_2 y_2 : x_M y_M
出力
T = 1 の場合は与えられたネットワークの均一的な状態をいずれかひとつ出力し、T = 2 の場合は非均一的な状態をいずれかひとつ出力せよ。ただし、そのような状態が存在しないなら -1 と出力せよ。
入力例 1
4 5 1 1 3 2 4 1 2 3 4 2 3
出力例 1
^^^^^
どのケーブルから流れ始めてもコインはケーブル 1 に行き着くため、この状態は均一的です。
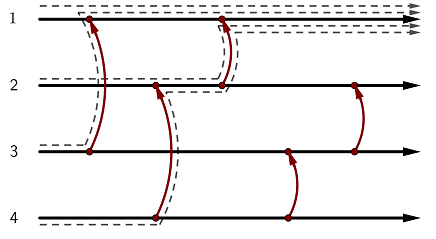
入力例 2
4 5 2 1 3 2 4 1 2 3 4 2 3
出力例 2
v^^^^
流れ始めるケーブル次第で、コインはケーブル 1 にもケーブル 2 にも行き着くことがあるため、この状態は非均一的です。
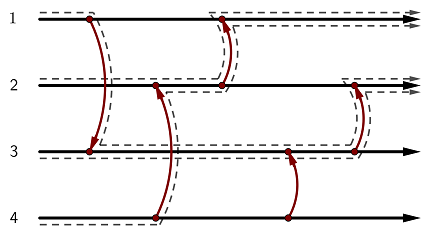
入力例 3
3 1 1 1 2
出力例 3
-1
均一的な状態が存在しません。
入力例 4
2 1 2 1 2
出力例 4
-1
非均一的な状態が存在しません。
Score : 1600 points
Problem Statement
A balancing network is an abstract device built up of N wires, thought of as running from left to right, and M balancers that connect pairs of wires. The wires are numbered from 1 to N from top to bottom, and the balancers are numbered from 1 to M from left to right. Balancer i connects wires x_i and y_i (x_i < y_i).

Each balancer must be in one of two states: up or down.
Consider a token that starts moving to the right along some wire at a point to the left of all balancers. During the process, the token passes through each balancer exactly once. Whenever the token encounters balancer i, the following happens:
- If the token is moving along wire x_i and balancer i is in the down state, the token moves down to wire y_i and continues moving to the right.
- If the token is moving along wire y_i and balancer i is in the up state, the token moves up to wire x_i and continues moving to the right.
- Otherwise, the token doesn't change the wire it's moving along.
Let a state of the balancing network be a string of length M, describing the states of all balancers.
The i-th character is ^ if balancer i is in the up state, and v if balancer i is in the down state.
A state of the balancing network is called uniforming if a wire w exists such that, regardless of the starting wire, the token will always end up at wire w and run to infinity along it. Any other state is called non-uniforming.
You are given an integer T (1 \le T \le 2). Answer the following question:
- If T = 1, find any uniforming state of the network or determine that it doesn't exist.
- If T = 2, find any non-uniforming state of the network or determine that it doesn't exist.
Note that if you answer just one kind of questions correctly, you can get partial score.
Constraints
- 2 \leq N \leq 50000
- 1 \leq M \leq 100000
- 1 \leq T \leq 2
- 1 \leq x_i < y_i \leq N
- All input values are integers.
Partial Score
- 800 points will be awarded for passing the testset satisfying T = 1.
- 800 points will be awarded for passing the testset satisfying T = 2.
Input
Input is given from Standard Input in the following format:
N M T x_1 y_1 x_2 y_2 : x_M y_M
Output
Print any uniforming state of the given network if T = 1, or any non-uniforming state if T = 2. If the required state doesn't exist, output -1.
Sample Input 1
4 5 1 1 3 2 4 1 2 3 4 2 3
Sample Output 1
^^^^^
This state is uniforming: regardless of the starting wire, the token ends up at wire 1.

Sample Input 2
4 5 2 1 3 2 4 1 2 3 4 2 3
Sample Output 2
v^^^^
This state is non-uniforming: depending on the starting wire, the token might end up at wire 1 or wire 2.

Sample Input 3
3 1 1 1 2
Sample Output 3
-1
A uniforming state doesn't exist.
Sample Input 4
2 1 2 1 2
Sample Output 4
-1
A non-uniforming state doesn't exist.
Time Limit: 4 sec / Memory Limit: 1024 MB
配点 : 2000 点
問題文
N 行 N 列のマスからなる盤面を考えます。アーボックはこの盤面の一部を切り離し、i = 1, 2, \ldots, N のそれぞれについて、左から i 列目は最も下の h_i マスのみが残されています。 そして、残されたマスのうち何マスかにルークを置こうとしています。
ルークはチェスの駒の一種で、1 マスを占めます。1 回の移動では、何も置かれていないマスの上を縦か横の一方向に何マスでも動けます。 切り離されたマスの上は通れません。
あるマスについて、そのマスにルークが置かれているか、そのマスに 1 回の移動で到達できるルークがあるとき、そのマスは支配下にあるといいます。
残された全マスが支配下に入るように残されたマスのうち何マスかにルークを置く方法の数を 998244353 で割った余りを求めてください。
制約
- 1 \leq N \leq 400
- 1 \leq h_i \leq N
- 入力中のすべての値は整数である。
入力
入力は以下の形式で標準入力から与えられる。
N h_1 h_2 ... h_N
出力
残された全マスが支配下に入るように残されたマスのうち何マスかにルークを置く方法の数を 998244353 で割った余りを出力せよ。
入力例 1
2 2 2
出力例 1
11
2 個以上のルークをどのように置いても条件が満たされ、そのような置き方は 11 通りです。
入力例 2
3 2 1 2
出力例 2
17
条件を満たす置き方は次の 17 通りです (R がルーク、* が空のマスに対応)。
R * * R * * R R R R R R **R R** R*R R** *R* **R R * R * * R * R * * R R R*R *RR RR* R*R RRR RR* R R R R R * * R R R R*R *RR RRR RRR RRR
入力例 3
4 1 2 4 1
出力例 3
201
入力例 4
10 4 7 4 8 4 6 8 2 3 6
出力例 4
263244071
Score : 2000 points
Problem Statement
Let us consider a grid of squares with N rows and N columns. Arbok has cut out some part of the grid so that, for each i = 1, 2, \ldots, N, the bottommost h_i squares are remaining in the i-th column from the left. Now, he wants to place rooks into some of the remaining squares.
A rook is a chess piece that occupies one square and can move horizontally or vertically, through any number of unoccupied squares. A rook can not move through squares that have been cut out by Arbok.
Let's say that a square is covered if it either contains a rook, or a rook can be moved to this square in one move.
Find the number of ways to place rooks into some of the remaining squares so that every remaining square is covered, modulo 998244353.
Constraints
- 1 \leq N \leq 400
- 1 \leq h_i \leq N
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N h_1 h_2 ... h_N
Output
Print the number of ways to place rooks into some of the remaining squares so that every remaining square is covered, modulo 998244353.
Sample Input 1
2 2 2
Sample Output 1
11
Any placement with at least two rooks is fine. There are 11 such placements.
Sample Input 2
3 2 1 2
Sample Output 2
17
The following 17 rook placements satisfy the conditions (R denotes a rook, * denotes an empty square):
R * * R * * R R R R R R **R R** R*R R** *R* **R R * R * * R * R * * R R R*R *RR RR* R*R RRR RR* R R R R R * * R R R R*R *RR RRR RRR RRR
Sample Input 3
4 1 2 4 1
Sample Output 3
201
Sample Input 4
10 4 7 4 8 4 6 8 2 3 6
Sample Output 4
263244071