Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 300 点
問題文
N 項からなる数列 A_1,...,A_N があり、N 個のボタンがあります。 i(1 ≦ i ≦ N) 個目のボタンを押すと、数列 A の 1 項目から i 項目までの値が 1 ずつ増加します。
数列 B_1,...,B_N が与えられます。高橋君は、これらのボタンを何回か押して、すべての i に対し、A_i が B_i の倍数になるようにします。
高橋君がボタンを押す回数の最小値を求めてください。
制約
- 入力はすべて整数である。
- 1 ≦ N ≦ 10^5
- 0 ≦ A_i ≦ 10^9(1 ≦ i ≦ N)
- 1 ≦ B_i ≦ 10^9(1 ≦ i ≦ N)
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 : A_N B_N
出力
高橋君がボタンを押す回数の最小値を表す整数を出力せよ。
入力例 1
3 3 5 2 7 9 4
出力例 1
7
1 つめのボタンを 2 回、2 つめのボタンを 2 回、3 つめのボタンを 3 回押せばよいです。
入力例 2
7 3 1 4 1 5 9 2 6 5 3 5 8 9 7
出力例 2
22
Score : 300 points
Problem Statement
There are an integer sequence A_1,...,A_N consisting of N terms, and N buttons. When the i-th (1 ≦ i ≦ N) button is pressed, the values of the i terms from the first through the i-th are all incremented by 1.
There is also another integer sequence B_1,...,B_N. Takahashi will push the buttons some number of times so that for every i, A_i will be a multiple of B_i.
Find the minimum number of times Takahashi will press the buttons.
Constraints
- All input values are integers.
- 1 ≦ N ≦ 10^5
- 0 ≦ A_i ≦ 10^9(1 ≦ i ≦ N)
- 1 ≦ B_i ≦ 10^9(1 ≦ i ≦ N)
Input
The input is given from Standard Input in the following format:
N A_1 B_1 : A_N B_N
Output
Print an integer representing the minimum number of times Takahashi will press the buttons.
Sample Input 1
3 3 5 2 7 9 4
Sample Output 1
7
Press the first button twice, the second button twice and the third button three times.
Sample Input 2
7 3 1 4 1 5 9 2 6 5 3 5 8 9 7
Sample Output 2
22
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 800 点
問題文
N 人の人が大会に出場しました。この大会はトーナメント形式であり、N-1 回の試合が行われました。 諸事情により、このトーナメントは全参加者に平等に組まれているとは限りません。 すなわち、各人に対し、優勝するために必要なその人が勝者となるような試合数が等しいとは限りません。 トーナメントの構造は、正式には問題文の末尾で定義されます。
各試合では必ず片方の人が勝者、もう片方の人が敗者となり、最後まで負けなかった 1 人が優勝となります。
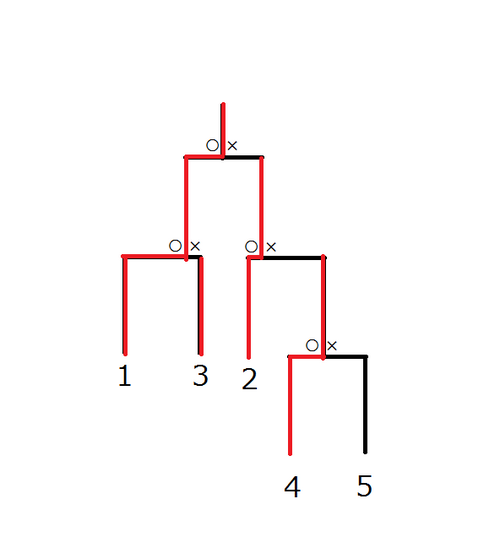
図: トーナメントの例
人には 1 から N までの番号がついており、1 番の人が優勝し、優勝者以外の人 i(2 ≦ i ≦ N) は人 a_i との試合で負けました。
トーナメントの深さとは、すべての人に対する、その人が優勝するために必要な、その人が勝者となるような試合数の最大値です。
トーナメントの深さとしてありうる最小の値を求めてください。
トーナメントの構造の正式な定義は以下の通りです。i 回目の試合では、
- あらかじめ決められた、まだ試合をしていない 2 人の人
- あらかじめ決められたまだ試合をしていない人 1 人と、あらかじめ決められた j(j<i) に対する、j 回目の試合の勝者
- あらかじめ決められた j,k(j,k<i, j ≠ k) に対する、j 回目の試合の勝者と k 回目の試合の勝者
のうちのいずれかの 2 人が試合を行います。このような構造であって、どのように試合結果を決めても、すでに一度試合に負けた人が再び試合をすることのないようなものをトーナメントと呼びます。
制約
- 2 ≦ N ≦ 10^5
- 1 ≦ a_i ≦ N(2 ≦ i ≦ N)
- 入力の試合結果と合致するようなトーナメントが存在する
入力
入力は以下の形式で標準入力から与えられる。
N a_2 : a_N
出力
トーナメントの深さとしてありうる最小の値を出力せよ。
入力例 1
5 1 1 2 4
出力例 1
3
次のような試合結果が条件を満たします。
- 1 回目の試合では、人 4 と 人 5 が対戦し、人 4 が勝つ
- 2 回目の試合では、人 2 と 人 4 が対戦し、人 2 が勝つ
- 3 回目の試合では、人 1 と 人 3 が対戦し、人 1 が勝つ
- 4 回目の試合では、人 1 と 人 2 が対戦し、人 1 が勝つ

このトーナメントは、人 5 が優勝するためには 3 回勝利する必要があるので、深さ 3 のトーナメントとなります。 逆に、深さ 2 以下の条件を満たすトーナメントは存在しないので、3 を出力します。
入力例 2
7 1 2 1 3 1 4
出力例 2
3
入力例 3
4 4 4 1
出力例 3
3
Score : 800 points
Problem Statement
N contestants participated in a competition. The total of N-1 matches were played in a knockout tournament. For some reasons, the tournament may not be "fair" for all the contestants. That is, the number of the matches that must be played in order to win the championship may be different for each contestant. The structure of the tournament is formally described at the end of this statement.
After each match, there were always one winner and one loser. The last contestant standing was declared the champion.

Figure: an example of a tournament
For convenience, the contestants were numbered 1 through N. The contestant numbered 1 was the champion, and the contestant numbered i(2 ≦ i ≦ N) was defeated in a match against the contestant numbered a_i.
We will define the depth of the tournament as the maximum number of the matches that must be played in order to win the championship over all the contestants.
Find the minimum possible depth of the tournament.
The formal description of the structure of the tournament is as follows. In the i-th match, one of the following played against each other:
- Two predetermined contestants
- One predetermined contestant and the winner of the j-th match, where j(j<i) was predetermined
- The winner of the j-th match and the winner of the k-th match, where j and k (j,k<i, j ≠ k) were predetermined
Such structure is valid structure of the tournament, if and only if no contestant who has already been defeated in a match will never play in a match, regardless of the outcome of the matches.
Constraints
- 2 ≦ N ≦ 10^5
- 1 ≦ a_i ≦ N(2 ≦ i ≦ N)
- It is guaranteed that the input is consistent (that is, there exists at least one tournament that matches the given information).
Input
The input is given from Standard Input in the following format:
N a_2 : a_N
Output
Print the minimum possible depth of the tournament.
Sample Input 1
5 1 1 2 4
Sample Output 1
3
The following tournament and the result of the matches are consistent with the given information:
- In the first match, contestants 4 and 5 played against each other, and contestant 4 won.
- In the second match, contestants 2 and 4 played against each other, and contestant 2 won.
- In the third match, contestants 1 and 3 played against each other, and contestant 1 won.
- In the fourth match, contestants 1 and 2 played against each other, and contestant 1 won.

The depth of this tournament is 3, since contestant 5 must play three matches in order to win the championship. There is no tournament with depth 2 or less that is consistent with the given information, thus the output should be 3.
Sample Input 2
7 1 2 1 3 1 4
Sample Output 2
3
Sample Input 3
4 4 4 1
Sample Output 3
3
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1100 点
問題文
相異なる整数 N 個からなる集合があります。この集合の i 番目に小さい要素は S_i です。この集合を X,Y の 2 つの集合に分割し、
- X に属するどの相異なる 2 つの要素も、その差の絶対値が A 以上
- Y に属するどの相異なる 2 つの要素も、その差の絶対値が B 以上
になるようにしたいです。このような分割としてありうるものの個数を 10^9 + 7 で割ったあまりを求めてください。ただし、X,Y のうち一方が空となるような分割も数えます。
制約
- 入力はすべて整数である。
- 1 ≦ N ≦ 10^5
- 1 ≦ A , B ≦ 10^{18}
- 0 ≦ S_i ≦ 10^{18}(1 ≦ i ≦ N)
- S_i < S_{i+1}(1 ≦ i ≦ N - 1)
入力
入力は以下の形式で標準入力から与えられる。
N A B S_1 : S_N
出力
条件を満たす分割の個数を 10^9 + 7 で割ったあまりを出力せよ。
入力例 1
5 3 7 1 3 6 9 12
出力例 1
5
次の 5 通りの分割方法があります。
- X={1,6,9,12}, Y={3}
- X={1,6,9}, Y={3,12}
- X={3,6,9,12}, Y={1}
- X={3,6,9}, Y={1,12}
- X={3,6,12}, Y={1,9}
入力例 2
7 5 3 0 2 4 7 8 11 15
出力例 2
4
入力例 3
8 2 9 3 4 5 13 15 22 26 32
出力例 3
13
入力例 4
3 3 4 5 6 7
出力例 4
0
Score : 1100 points
Problem Statement
There is a set consisting of N distinct integers. The i-th smallest element in this set is S_i. We want to divide this set into two sets, X and Y, such that:
- The absolute difference of any two distinct elements in X is A or greater.
- The absolute difference of any two distinct elements in Y is B or greater.
How many ways are there to perform such division, modulo 10^9 + 7? Note that one of X and Y may be empty.
Constraints
- All input values are integers.
- 1 ≦ N ≦ 10^5
- 1 ≦ A , B ≦ 10^{18}
- 0 ≦ S_i ≦ 10^{18}(1 ≦ i ≦ N)
- S_i < S_{i+1}(1 ≦ i ≦ N - 1)
Input
The input is given from Standard Input in the following format:
N A B S_1 : S_N
Output
Print the number of the different divisions under the conditions, modulo 10^9 + 7.
Sample Input 1
5 3 7 1 3 6 9 12
Sample Output 1
5
There are five ways to perform division:
- X={1,6,9,12}, Y={3}
- X={1,6,9}, Y={3,12}
- X={3,6,9,12}, Y={1}
- X={3,6,9}, Y={1,12}
- X={3,6,12}, Y={1,9}
Sample Input 2
7 5 3 0 2 4 7 8 11 15
Sample Output 2
4
Sample Input 3
8 2 9 3 4 5 13 15 22 26 32
Sample Output 3
13
Sample Input 4
3 3 4 5 6 7
Sample Output 4
0
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1400 点
問題文
以下のように、木がウニ度 k であるということを再帰的に定義します。
- 1 頂点からなる木はウニ度 0 の木である。
- ウニ度 k の木を 0 個以上と、ひとつの頂点 v を用意する。用意した各ウニ度 k の木から頂点をひとつずつ選び、その選んだ頂点と v を辺で結ぶ。こうしてできた木はウニ度 k+1 の木である。
ウニ度 k の木はウニ度 k+1,k+2,... の木でもあることが証明できます。
N 頂点からなる木が与えられます。 この木の頂点には 1 から N までの番号がついており、N-1 本の辺のうちの i 本目は頂点 a_i と b_i を結んでいます。
与えられた木がウニ度 k であるような最小の k を求めてください。
制約
- 2 ≦ N ≦ 10^5
- 1 ≦ a_i, b_i ≦ N(1 ≦ i ≦ N-1)
- 与えられるグラフは木である。
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 b_1
:
a_{N-1} b_{N-1}
出力
与えられた木がウニ度 k であるような最小の k を出力せよ。
入力例 1
7 1 2 2 3 2 4 4 6 6 7 7 5
出力例 1
2
頂点 1 からなるウニ度 0 の木と、頂点 3 からなるウニ度 0 の木と、頂点 4 からなるウニ度 0 の木と、 頂点 2 を組み合わせることで頂点 1,2,3,4 からなるウニ度 1 の木を作ることができ、
頂点 5 からなるウニ度 0 の木と、 頂点 7 を組み合わせることで頂点 5,7 からなるウニ度 1 の木を作ることができ、
頂点 1,2,3,4 からなるウニ度 1 の木と、頂点 5,7 からなるウニ度 1 の木と、 頂点 6 を組み合わせることで頂点 1,2,3,4,5,6,7 からなるウニ度 2 の木を作ることができます。
入力例 2
12 1 2 2 3 2 4 4 5 5 6 6 7 7 8 5 9 9 10 10 11 11 12
出力例 2
3
Score : 1400 points
Problem Statement
We will recursively define uninity of a tree, as follows: (Uni is a Japanese word for sea urchins.)
- A tree consisting of one vertex is a tree of uninity 0.
- Suppose there are zero or more trees of uninity k, and a vertex v. If a vertex is selected from each tree of uninity k and connected to v with an edge, the resulting tree is a tree of uninity k+1.
It can be shown that a tree of uninity k is also a tree of uninity k+1,k+2,..., and so forth.
You are given a tree consisting of N vertices. The vertices of the tree are numbered 1 through N, and the i-th of the N-1 edges connects vertices a_i and b_i.
Find the minimum k such that the given tree is a tree of uninity k.
Constraints
- 2 ≦ N ≦ 10^5
- 1 ≦ a_i, b_i ≦ N(1 ≦ i ≦ N-1)
- The given graph is a tree.
Input
The input is given from Standard Input in the following format:
N
a_1 b_1
:
a_{N-1} b_{N-1}
Output
Print the minimum k such that the given tree is a tree of uninity k.
Sample Input 1
7 1 2 2 3 2 4 4 6 6 7 7 5
Sample Output 1
2
A tree of uninity 1 consisting of vertices 1, 2, 3 and 4 can be constructed from the following: a tree of uninity 0 consisting of vertex 1, a tree of uninity 0 consisting of vertex 3, a tree of uninity 0 consisting of vertex 4, and vertex 2.
A tree of uninity 1 consisting of vertices 5 and 7 can be constructed from the following: a tree of uninity 1 consisting of vertex 5, and vertex 7.
A tree of uninity 2 consisting of vertices 1, 2, 3, 4, 5, 6 and 7 can be constructed from the following: a tree of uninity 1 consisting of vertex 1, 2, 3 and 4, a tree of uninity 1 consisting of vertex 5 and 7, and vertex 6.
Sample Input 2
12 1 2 2 3 2 4 4 5 5 6 6 7 7 8 5 9 9 10 10 11 11 12
Sample Output 2
3
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1600 点
問題文
黒板に、N 個の 0 と M 個の 1 が書かれています。 この状態から、黒板に書かれている有理数のうち K 個を選んで消し、それら K 個の有理数の平均を新たに書き加える操作を繰り返します。 ただし、N+M-1 は K-1 で割り切れるものとします。
このとき、操作ができなくなるまでこの操作を繰り返すと最終的に黒板には 1 つの有理数が書かれた状態になります。
この残った有理数の値としてありうるものの個数を 10^9 + 7 で割ったあまりを求めてください。
制約
- 1 ≦ N, M ≦ 2000
- 2 ≦ K ≦ 2000
- N+M-1 は K-1 で割り切れる。
入力
入力は以下の形式で標準入力から与えられる。
N M K
出力
最後に残った有理数の値としてありうるものの個数を 10^9 + 7 で割ったあまりを出力せよ。
入力例 1
2 2 2
出力例 1
5
最後に残る有理数としてありうるものは、\frac{1}{4}, \frac{3}{8}, \frac{1}{2}, \frac{5}{8}, \frac{3}{4} の 5 通りです。
例えば \frac{3}{8} は、以下のような操作で最後に残ります。
- 0,1 を消して \frac{1}{2} を書く。
- \frac{1}{2},1 を消して \frac{3}{4} を書く。
- 0,\frac{3}{4} を消して \frac{3}{8} を書く。
入力例 2
3 4 3
出力例 2
9
入力例 3
150 150 14
出力例 3
937426930
Score : 1600 points
Problem Statement
There are N zeros and M ones written on a blackboard. Starting from this state, we will repeat the following operation: select K of the rational numbers written on the blackboard and erase them, then write a new number on the blackboard that is equal to the arithmetic mean of those K numbers. Here, assume that N + M - 1 is divisible by K - 1.
Then, if we repeat this operation until it is no longer applicable, there will be eventually one rational number left on the blackboard.
Find the number of the different possible values taken by this rational number, modulo 10^9 + 7.
Constraints
- 1 ≦ N, M ≦ 2000
- 2 ≦ K ≦ 2000
- N + M - 1 is divisible by K - 1.
Input
The input is given from Standard Input in the following format:
N M K
Output
Print the number of the different possible values taken by the rational number that will be eventually left on the blackboard, modulo 10^9 + 7.
Sample Input 1
2 2 2
Sample Output 1
5
There are five possible values for the number that will be eventually left on the blackboard: \frac{1}{4}, \frac{3}{8}, \frac{1}{2}, \frac{5}{8} and \frac{3}{4}.
For example, \frac{3}{8} can be eventually left if we:
- Erase 0 and 1, then write \frac{1}{2}.
- Erase \frac{1}{2} and 1, then write \frac{3}{4}.
- Erase 0 and \frac{3}{4}, then write \frac{3}{8}.
Sample Input 2
3 4 3
Sample Output 2
9
Sample Input 3
150 150 14
Sample Output 3
937426930