実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 200 点
問題文
縦 H 行、横 W 列のマス目に区切られた盤面があります。 はじめ、駒が左上隅のマスに置かれていました。 シックはこの駒を 1 マスずつ上下左右に動かし、右下隅のマスに移動させました。 このとき、駒が同じマスを複数回通った可能性もあります(左上隅や右下隅のマスも含む)。
縦横に並んだ文字 a_{ij} (1 \leq i \leq H, 1 \leq j \leq W) が与えられます。
a_{ij} が # のとき、駒が移動する過程で i 行 j 列目のマスを一度以上通ったことを表します(左上隅や右下隅のマスは必ず通ったものとして扱います)。
a_{ij} が . のとき、駒が i 行 j 列目のマスを一度も通らなかったことを表します。
移動する過程で、駒が常に右または下に動いていた可能性があるか判定してください。
制約
- 2 \leq H, W \leq 8
- a_{i,j} は
#または.である。 - 問題文および a で与えられる情報と整合するような駒の動き方が存在する。
入力
入力は以下の形式で標準入力から与えられる。
H W
A_{11}A_{12}...A_{1W}
:
A_{H1}A_{H2}...A_{HW}
出力
移動する過程で、駒が常に右または下に動いていた可能性があれば Possible 、なければ Impossible と出力せよ。
入力例 1
4 5 ##... .##.. ..##. ...##
出力例 1
Possible
右、下、右、下、右、下、右と駒が動くと、通るマスが与えられた情報と合致します。
入力例 2
5 3 ### ..# ### #.. ###
出力例 2
Impossible
入力例 3
4 5 ##... .###. .###. ...##
出力例 3
Impossible
Score : 200 points
Problem Statement
We have a grid of H rows and W columns. Initially, there is a stone in the top left cell. Shik is trying to move the stone to the bottom right cell. In each step, he can move the stone one cell to its left, up, right, or down (if such cell exists). It is possible that the stone visits a cell multiple times (including the bottom right and the top left cell).
You are given a matrix of characters a_{ij} (1 \leq i \leq H, 1 \leq j \leq W). After Shik completes all moving actions, a_{ij} is # if the stone had ever located at the i-th row and the j-th column during the process of moving. Otherwise, a_{ij} is .. Please determine whether it is possible that Shik only uses right and down moves in all steps.
Constraints
- 2 \leq H, W \leq 8
- a_{i,j} is either
#or.. - There exists a valid sequence of moves for Shik to generate the map a.
Input
The input is given from Standard Input in the following format:
H W
a_{11}a_{12}...a_{1W}
:
a_{H1}a_{H2}...a_{HW}
Output
If it is possible that Shik only uses right and down moves, print Possible. Otherwise, print Impossible.
Sample Input 1
4 5 ##... .##.. ..##. ...##
Sample Output 1
Possible
The matrix can be generated by a 7-move sequence: right, down, right, down, right, down, and right.
Sample Input 2
5 3 ### ..# ### #.. ###
Sample Output 2
Impossible
Sample Input 3
4 5 ##... .###. .###. ...##
Sample Output 3
Impossible
実行時間制限: 2 sec / メモリ制限: 256 MiB
Score : 400 points
Problem Statement
You are given a permutation p of the set {1, 2, ..., N}. Please construct two sequences of positive integers a_1, a_2, ..., a_N and b_1, b_2, ..., b_N satisfying the following conditions:
- 1 \leq a_i, b_i \leq 10^9 for all i
- a_1 < a_2 < ... < a_N
- b_1 > b_2 > ... > b_N
- a_{p_1}+b_{p_1} < a_{p_2}+b_{p_2} < ... < a_{p_N}+b_{p_N}
Constraints
- 2 \leq N \leq 20,000
- p is a permutation of the set {1, 2, ..., N}
Input
The input is given from Standard Input in the following format:
N p_1 p_2 ... p_N
Output
The output consists of two lines. The first line contains a_1, a_2, ..., a_N seperated by a space. The second line contains b_1, b_2, ..., b_N seperated by a space.
It can be shown that there always exists a solution for any input satisfying the constraints.
Sample Input 1
2 1 2
Sample Output 1
1 4 5 4
a_1 + b_1 = 6 and a_2 + b_2 = 8. So this output satisfies all conditions.
Sample Input 2
3 3 2 1
Sample Output 2
1 2 3 5 3 1
Sample Input 3
3 2 3 1
Sample Output 3
5 10 100 100 10 1
配点 : 400 点
問題文
集合 {1, 2, ..., N} の要素を並び替えた順列 p が与えられます。以下の条件をすべて満たす 2 つの正整数列 a_1, a_2, ..., a_N および b_1, b_2, ..., b_N を構成してください。
- すべての i に対し、1 \leq a_i, b_i \leq 10^9
- a_1 < a_2 < ... < a_N
- b_1 > b_2 > ... > b_N
- a_{p_1}+b_{p_1} < a_{p_2}+b_{p_2} < ... < a_{p_N}+b_{p_N}
制約
- 2 \leq N \leq 20,000
- p は集合 {1, 2, ..., N} の要素を並び替えた順列である。
入力
入力は以下の形式で標準入力から与えられる。
N p_1 p_2 ... p_N
Output
2 行出力せよ。1 行目に整数列 a_1, a_2, ..., a_N を、2 行目に整数列 b_1, b_2, ..., b_N を、それぞれ空白区切りで出力せよ。
なお、制約を満たす任意の入力に対して解が存在することが示せる。
入力例 1
2 1 2
出力例 1
1 4 5 4
a_1 + b_1 = 6 および a_2 + b_2 = 8 より、すべての条件が満たされています。
入力例 2
3 3 2 1
出力例 2
1 2 3 5 3 1
入力例 3
3 2 3 1
出力例 3
5 10 100 100 10 1
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1000 点
問題文
N 個の球と N+1 個の穴が一直線上に並んでいます。球には左から順に 1 から N の番号が、穴には左から順に 1 から N+1 の番号が振られています。i 番の球は i 番の穴と i+1 番の穴の間に置かれており、隣り合う穴と球の間の距離を左から順に並べて得られる数列を d_i (1 \leq i \leq 2 \times N) とおきます。d_1 の値とパラメータ x が与えられており、d_i - d_{i-1} = x が任意の i (2 \leq i \leq 2 \times N) に対して成り立っています。
これら N 個の球を 1 個ずつ転がし、穴に落としていくことを考えます。球が穴の上を通ると、その穴にすでに別の球が入っていなければその穴に落ちます。すでに別の球がその穴に入っていた場合は、球は落ちずにそのまま転がり続けます。(なお、この問題で考える球の転がし方において、球どうしが衝突することはありません。)
球を転がす際は、まだ転がされていない球の中から等確率で 1 つを選び、その球を左または右に等確率で転がします。これを N 回繰り返してすべての球を転がすとき、すべての球が移動する距離の総和の期待値を求めてください。
以下に N = 3, d_1 = 1, x = 1 の場合の球の転がし方の例を挙げます。
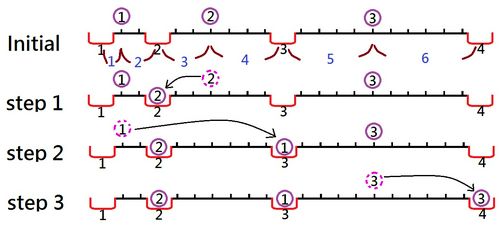
- 2 番の球を左に転がす。球は 2 番の穴に落ちる。球が移動する距離は 3 である。
- 1 番の球を右に転がす。球は 2 番の穴の上を通り、3 番の穴に落ちる。球が移動する距離は 9 である。
- 3 番の球を右に転がす。球は 4 番の穴に落ちる。球が移動する距離は 6 である。
この例では、球が移動する距離の総和は 18 となります。
なお、球をどのように転がしてもどの球も必ずいずれかの穴に落ち、最後に穴が一つだけ空のまま残ることになります。
制約
- 1 \leq N \leq 200,000
- 1 \leq d_1 \leq 100
- 0 \leq x \leq 100
- 入力値はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N d_1 x
出力
答えを小数で出力せよ。絶対誤差または相対誤差のいずれかが 10^{-9} 以内でなければならない。
入力例 1
1 3 3
出力例 1
4.500000000000000
球が 1 個、穴が 2 個あります。球から左の穴までの距離は 3 、球から右の穴までの距離は 6 です。球を左に転がすか右に転がすかの 2 通りの転がし方があり、それぞれにおいて球が移動する距離は 3, 6 です。したがって、答えは (3+6)/2 = 4.5 となります。
入力例 2
2 1 0
出力例 2
2.500000000000000
入力例 3
1000 100 100
出力例 3
649620280.957660079002380
Score : 1000 points
Problem Statement
There are N balls and N+1 holes in a line. Balls are numbered 1 through N from left to right. Holes are numbered 1 through N+1 from left to right. The i-th ball is located between the i-th hole and (i+1)-th hole. We denote the distance between neighboring items (one ball and one hole) from left to right as d_i (1 \leq i \leq 2 \times N). You are given two parameters d_1 and x. d_i - d_{i-1} is equal to x for all i (2 \leq i \leq 2 \times N).
We want to push all N balls into holes one by one. When a ball rolls over a hole, the ball will drop into the hole if there is no ball in the hole yet. Otherwise, the ball will pass this hole and continue to roll. (In any scenario considered in this problem, balls will never collide.)
In each step, we will choose one of the remaining balls uniformly at random and then choose a direction (either left or right) uniformly at random and push the ball in this direction. Please calculate the expected total distance rolled by all balls during this process.
For example, when N = 3, d_1 = 1, and x = 1, the following is one possible scenario:

- first step: push the ball numbered 2 to its left, it will drop into the hole numbered 2. The distance rolled is 3.
- second step: push the ball numbered 1 to its right, it will pass the hole numbered 2 and drop into the hole numbered 3. The distance rolled is 9.
- third step: push the ball numbered 3 to its right, it will drop into the hole numbered 4. The distance rolled is 6.
So the total distance in this scenario is 18.
Note that in all scenarios every ball will drop into some hole and there will be a hole containing no ball in the end.
Constraints
- 1 \leq N \leq 200,000
- 1 \leq d_1 \leq 100
- 0 \leq x \leq 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N d_1 x
Output
Print a floating number denoting the answer. The relative or absolute error of your answer should not be higher than 10^{-9}.
Sample Input 1
1 3 3
Sample Output 1
4.500000000000000
The distance between the only ball and the left hole is 3 and distance between the only ball and the right hole is 6. There are only two scenarios (i.e. push left and push right). The only ball will roll 3 and 6 unit distance, respectively. So the answer for this example is (3+6)/2 = 4.5.
Sample Input 2
2 1 0
Sample Output 2
2.500000000000000
Sample Input 3
1000 100 100
Sample Output 3
649620280.957660079002380
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1200 点
問題文
一直線上でゲームを行います。はじめプレイヤーは座標 0 におり、キャンディを N 個持っています。座標 E に出口があります。プレイヤーの他に、この直線上には N 匹のクマがおり、i 匹目のクマは座標 x_i で静止しています。プレイヤーは直線上を 1 以下の速度で動くことができます。
プレイヤーがクマにキャンディを 1 個与えると、クマは T 単位時間後に 1 枚のコインをその場に吐き出します。すなわち、時刻 t にクマにキャンディを 1 個与えると、時刻 t+T にそのクマの位置に 1 枚のコインが出現します。このゲームの目的は、N 匹すべてのクマにキャンディを与え、N 枚のコインをすべて回収して出口から脱出することです。クマにキャンディを与えるためには、プレイヤーはクマと同じ位置にいなければなりません。また、1 匹のクマに 2 回以上キャンディを与えることはできません。コインは、出現した瞬間以降にプレイヤーがコインと同じ位置にいれば回収できます。プレイヤーが回収する前にコインが消滅することはありません。
シックはこのゲームの達人です。シックがクマにキャンディを与えたり、コインを拾うのに必要な時間は極めて短く、無視することができます。ゲームの設定が与えられるので、シックがすべてのコインを集めて出口から脱出するまでに必要な最短時間を求めてください。
制約
- 1 \leq N \leq 100,000
- 1 \leq T, E \leq 10^9
- 0 < x_i < E
- x_i < x_{i+1} (1 \leq i < N)
- 入力値はすべて整数である。
部分点
- 600 点分のデータセットでは、N \leq 2,000 が成り立つ。
入力
入力は以下の形式で標準入力から与えられる。
N E T x_1 x_2 ... x_N
出力
シックがすべてのコインを集めて出口から脱出するまでに必要な最短時間を表す整数を出力せよ。
入力例 1
3 9 1 1 3 8
出力例 1
12
出口に向かいながら、クマに会うたびにキャンディを与え、その場でコインが出るのを待つのが最適です。このとき、移動に 9 単位時間、3 回の待機に 3 単位時間、合計で 12 単位時間を要します。
入力例 2
3 9 3 1 3 8
出力例 2
16
入力例 3
2 1000000000 1000000000 1 999999999
出力例 3
2999999996
Score : 1200 points
Problem Statement
Imagine a game played on a line. Initially, the player is located at position 0 with N candies in his possession, and the exit is at position E. There are also N bears in the game. The i-th bear is located at x_i. The maximum moving speed of the player is 1 while the bears do not move at all.
When the player gives a candy to a bear, it will provide a coin after T units of time. More specifically, if the i-th bear is given a candy at time t, it will put a coin at its position at time t+T. The purpose of this game is to give candies to all the bears, pick up all the coins, and go to the exit. Note that the player can only give a candy to a bear if the player is at the exact same position of the bear. Also, each bear will only produce a coin once. If the player visits the position of a coin after or at the exact same time that the coin is put down, the player can pick up the coin. Coins do not disappear until collected by the player.
Shik is an expert of this game. He can give candies to bears and pick up coins instantly. You are given the configuration of the game. Please calculate the minimum time Shik needs to collect all the coins and go to the exit.
Constraints
- 1 \leq N \leq 100,000
- 1 \leq T, E \leq 10^9
- 0 < x_i < E
- x_i < x_{i+1} for 1 \leq i < N
- All input values are integers.
Partial Scores
- In test cases worth 600 points, N \leq 2,000.
Input
The input is given from Standard Input in the following format:
N E T x_1 x_2 ... x_N
Output
Print an integer denoting the answer.
Sample Input 1
3 9 1 1 3 8
Sample Output 1
12
The optimal strategy is to wait for the coin after treating each bear. The total time spent on waiting is 3 and moving is 9. So the answer is 3 + 9 = 12.
Sample Input 2
3 9 3 1 3 8
Sample Output 2
16
Sample Input 3
2 1000000000 1000000000 1 999999999
Sample Output 3
2999999996
実行時間制限: 5 sec / メモリ制限: 256 MiB
Score : 1400 points
Problem Statement
In the country there are N cities numbered 1 through N, which are connected by N-1 bidirectional roads. In terms of graph theory, there is a unique simple path connecting every pair of cities. That is, the N cities form a tree. Besides, if we view city 1 as the root of this tree, the tree will be a full binary tree (a tree is a full binary tree if and only if every non-leaf vertex in the tree has exactly two children). Roads are numbered 1 through N-1. The i-th road connects city i+1 and city a_i. When you pass through road i, the toll you should pay is v_i (if v_i is 0, it indicates the road does not require a toll).
A company in city 1 will give each employee a family travel and cover a large part of the tolls incurred. Each employee can design the travel by themselves. That is, which cities he/she wants to visit in each day and which city to stay at each night. However, there are some constraints. More details are as follows:
-
The travel must start and end at city 1. If there are m leaves in the tree formed by the cities, then the number of days in the travel must be m+1. At the end of each day, except for the last day, the employee must stay at some hotel in a leaf city. During the whole travel, the employee must stay at all leaf cities exactly once.
-
During the whole travel, all roads of the country must be passed through exactly twice.
-
The amount that the employee must pay for tolls by him/herself is the maximum total toll incurred in a single day during the travel, except the first day and the last day. The remaining tolls will be covered by the company.
Shik, as an employee of this company, has only one hope for his travel. He hopes that the amount he must pay for tolls by himself will be as small as possible. Please help Shik to design the travel which satisfies his hope.
Constraints
- 2 < N < 131,072
- 1 \leq a_i \leq i for all i
- 0 \leq v_i \leq 131,072
- v_i is an integer
- The given tree is a full binary tree
Input
The input is given from Standard Input in the following format:
N
a_1 v_1
a_2 v_2
:
a_{N-1} v_{N-1}
Output
Print an integer denoting the minimum amount Shik must pay by himself for tolls incurred during the travel.
Sample Input 1
7 1 1 1 1 2 1 2 1 3 1 3 1
Sample Output 1
4
There are 4 leaves in the tree formed by the cities (cities 4, 5, 6, and 7), so the travel must be 5 days long. There are 4! = 24 possible arrangements of the leaf cities to stay during the travel, but some of them are invalid. For example, (4,5,6,7) and (6,7,5,4) are valid orders, but (5,6,7,4) is invalid because the route passes 4 times through the road connecting city 1 and city 2. The figure below shows the routes of the travel for these arrangements.
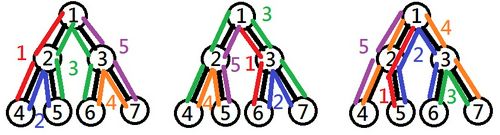
For all valid orders, day 3 is the day with the maximum total incurred toll of 4, passing through 4 roads.
Sample Input 2
9 1 2 1 2 3 2 3 2 5 2 5 2 7 2 7 2
Sample Output 2
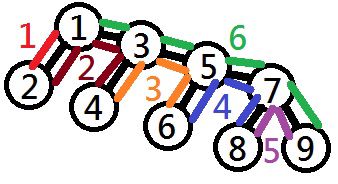
6
The following figure shows the route of the travel for one possible arrangement of the stayed cities for the solution. Note that the tolls incurred in the first day and the last day are always covered by the company.
Sample Input 3
15 1 2 1 5 3 3 4 3 4 3 6 5 5 4 5 3 6 3 3 2 11 5 11 3 13 2 13 1
Sample Output 3
15
Sample Input 4
3 1 0 1 0
Sample Output 4
0
配点 : 1400 点
問題文
ある国には N 個の都市があり、それらは N-1 本の道路で結ばれています。道路は双方向に通行できます。便宜上、都市には 1 から N の、道路には 1 から N-1 の番号が振られています。グラフ理論の用語を用いると、任意の二つの都市に対し、それらを結ぶ単純道がちょうど一つ存在します。すなわち、都市と道路から構成されるグラフは木です。また、1 番の都市をこの木の根とみなすと、この木は全二分木となっています。(全二分木とは、葉以外の任意の頂点がちょうど二つの子を持つような根付き木のことをいいます。)i 番の道路は i+1 番の都市と a_i 番の都市を結び、一回の通行ごとに v_i の通行料が発生します。(v_i が 0 であるような道路では通行料は発生しません。)
1 番の都市に、社員の旅行を奨励していることで有名な会社があります。この会社には道路通行料補助制度という制度があり、社員の旅行中に発生する道路の通行料のほとんどを会社が負担します。旅行がこの制度の適用対象となるためにはいくつかの制約を満たす必要があり、その範囲内であれば好きなように旅程を決めることができます。これらの詳細は以下の通りです。
-
制度の適用対象となるためには、旅行の出発点と終着点はともに 1 番の都市でなければならない。また、この国の都市と道路を 1 番の都市を根とする根付き木とみなしたとき、この木の葉の個数を m とすると、旅行日程は m 泊 m+1 日でなければならない。これらの m 回の宿泊は、木の葉に相当する都市のすべてで一度ずつ行わなければならない。
-
旅行全体を通じて、この国のすべての道路をそれぞれちょうど二度ずつ通行しなければならない。
-
旅行中に発生する道路の通行料のうち、社員自身が負担しなければならない金額は、発生する通行料の合計が最大であるような日(ただし旅行初日および最終日を除く)に発生する通行料の合計である。残りの金額は会社の負担となる。
シックはこの会社の従業員です。道路通行料補助制度のもとで行う今度の旅行では、発生する通行料のうち自分自身で支払わなければならない金額を最小にすることだけを考えています。そのような旅程を組む手伝いをしてあげてください。
制約
- 2 < N < 131,072
- すべての i に対し、1 \leq a_i \leq i
- 0 \leq v_i \leq 131,072
- v_i は整数である。
- 与えられる木は全二分木である。
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 v_1
a_2 v_2
.
.
a_{N-1} v_{N-1}
出力
道路通行料補助制度のもとで旅行を行うとき、発生する通行料のうち自分自身で負担しなければならない金額の最小値を出力せよ。
入力例 1
7 1 1 1 1 2 1 2 1 3 1 3 1
出力例 1
4
都市と道路を 1 番の都市を根とする根付き木とみなしたとき、この木には 4 個の葉が存在するため(4, 5, 6, 7 番の都市に相当する頂点)、 旅行日程は 4 泊 5 日となります。これらの 4 つの都市に宿泊する順序は 4! = 24 通り存在しますが、そのうちの一部では道路通行料補助制度の対象外となってしまいます。例えば、(4,5,6,7) や (6,7,5,4) の順に都市を訪れると制度の対象になりますが、(5,6,7,4) の順に訪れると経路中に 1 番の都市と 2 番の都市を結ぶ道路を 4 回通ってしまい、制度の対象外となってしまいます。下図にこれらの訪問順序に対応する旅行の経路を示します。

制度の対象となるような都市の訪問順序すべてにおいて、対応する旅程では 3 日目に 4 本の道路を通行して合計で 4 の通行料が発生し、発生する通行料の合計が最大であるような日はこの日となります。
入力例 2
9 1 2 1 2 3 2 3 2 5 2 5 2 7 2 7 2
出力例 2
6
下図に負担金額が最小となるような旅行の経路をひとつ示します。

負担金額を算出する際に、旅行初日および最終日に発生する通行料は考えないことに注意してください。
入力例 3
15 1 2 1 5 3 3 4 3 4 3 6 5 5 4 5 3 6 3 3 2 11 5 11 3 13 2 13 1
出力例 3
15
入力例 4
3 1 0 1 0
出力例 4
0
実行時間制限: 2 sec / メモリ制限: 256 MiB
Score : 1500 points
Problem Statement
Shik's job is very boring. At day 0, his boss gives him a string S_0 of length N which consists of only lowercase English letters. In the i-th day after day 0, Shik's job is to copy the string S_{i-1} to a string S_i. We denote the j-th letter of S_i as S_i[j].
Shik is inexperienced in this job. In each day, when he is copying letters one by one from the first letter to the last letter, he would make mistakes. That is, he sometimes accidentally writes down the same letter that he wrote previously instead of the correct one. More specifically, S_i[j] is equal to either S_{i-1}[j] or S_{i}[j-1]. (Note that S_i[1] always equals to S_{i-1}[1].)
You are given the string S_0 and another string T.
Please determine the smallest integer i such that S_i could be equal to T. If no such i exists, please print -1.
Constraints
- 1 \leq N \leq 1,000,000
- The lengths of S_0 and T are both N.
- Both S_0 and T consist of lowercase English letters.
Input
The input is given from Standard Input in the following format:
N S_0 T
Output
Print the smallest integer i such that S_i could be equal to T. If no such i exists, print -1 instead.
Sample Input 1
5 abcde aaacc
Sample Output 1
2
S_0 = abcde, S_1 = aaccc and S_2 = aaacc is a possible sequence such that S_2 = T.
Sample Input 2
5 abcde abcde
Sample Output 2
0
Sample Input 3
4 acaa aaca
Sample Output 3
2
Sample Input 4
5 abcde bbbbb
Sample Output 4
-1
配点 : 1500 点
問題文
シックの仕事はコピー取りです。ある日、シックは上司から英小文字からなる長さ N の文字列 S_0 を受け取りました(この日を 0 日目とします)。これ以降、i 日目の仕事は、文字列 S_{i-1} を S_i にコピーすることです。以下、S_i の j 番目の文字を S_i[j] と表します。
シックはまだこの仕事に慣れていません。毎日、文字列を先頭の文字から順に書き写していくのですが、正しい文字の代わりに誤って直前に書いた文字と同じ文字を書いてしまうことがあります。すなわち、S_i[j] は S_{i-1}[j] または S_{i}[j-1] のどちらかと等しくなります。(ただし、文字列の先頭の文字を書き間違えることはありません。すなわち、S_i[1] は必ず S_{i-1}[1] と等しくなります。)
二つの文字列 S_0 と T が与えられます。S_i が T と等しくなる可能性があるような最小の整数 i を求めてください。もしそのような i が存在しなければ、代わりに -1 と答えてください。
制約
- 1 \leq N \leq 1,000,000
- S_0 と T の長さはともに N である。
- S_0 と T はともに英小文字のみからなる。
入力
入力は以下の形式で標準入力から与えられる。
N S_0 T
出力
S_i が T と等しくなる可能性のあるような i が存在するならば、そのような i のうち最小のものを出力せよ。そのような i が存在しなければ、代わりに -1 と出力せよ。
入力例 1
5 abcde aaacc
出力例 1
2
S_0 = abcde, S_1 = aaccc, S_2 = aaacc のように、S_2 = T となる可能性が存在します。
入力例 2
5 abcde abcde
出力例 2
0
入力例 3
4 acaa aaca
出力例 3
2
入力例 4
5 abcde bbbbb
出力例 4
-1