実行時間制限: 1 sec / メモリ制限: 256 MiB
配点 : 300 点
問題文
文字列 X が与えられます。X の長さは偶数であり、半分は S 、もう半分は T からなります。
高橋君は ST という文字列が苦手です。なので以下の操作を 10^{10000} 回行うことにしました。
- X の(連続な)部分文字列で
STとなるもののうち、最も左側にあるものを取り除く。存在しないならば何もしない。
最終的に X は何文字になるかを求めてください。
制約
- 2 ≦ |X| ≦ 200,000
- X の長さは偶数
- X を構成する文字のうち半分は
Sであり、もう半分はTである
部分点
- 200 点分のデータセットでは |X| ≦ 200 が成り立つ
入力
入力は以下の形式で標準入力から与えられる。
X
出力
1 行に問題の答えを出力する。
入力例 1
TSTTSS
出力例 1
4
1 回目の操作では TSTTSS の 2,3 文字目が ST なので取り除きます。
X は TTSS になり、もう ST はないため残り 10^{10000}-1 回は何もしません。
よって答えは 4 となります。
入力例 2
SSTTST
出力例 2
0
SSTTST ⇒ STST ⇒ ST ⇒ `` となり、最終的に空文字列になります。
入力例 3
TSSTTTSS
出力例 3
4
TSSTTTSS ⇒ TSTTSS ⇒ TTSS となります。
Score : 300 points
Problem Statement
We have a string X, which has an even number of characters. Half the characters are S, and the other half are T.
Takahashi, who hates the string ST, will perform the following operation 10^{10000} times:
- Among the occurrences of
STin X as (contiguous) substrings, remove the leftmost one. If there is no occurrence, do nothing.
Find the eventual length of X.
Constraints
- 2 ≦ |X| ≦ 200,000
- The length of X is even.
- Half the characters in X are
S, and the other half areT.
Partial Scores
- In test cases worth 200 points, |X| ≦ 200.
Input
The input is given from Standard Input in the following format:
X
Output
Print the eventual length of X.
Sample Input 1
TSTTSS
Sample Output 1
4
In the 1-st operation, the 2-nd and 3-rd characters of TSTTSS are removed.
X becomes TTSS, and since it does not contain ST anymore, nothing is done in the remaining 10^{10000}-1 operations.
Thus, the answer is 4.
Sample Input 2
SSTTST
Sample Output 2
0
X will eventually become an empty string: SSTTST ⇒ STST ⇒ ST ⇒ ``.
Sample Input 3
TSSTTTSS
Sample Output 3
4
X will become: TSSTTTSS ⇒ TSTTSS ⇒ TTSS.
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 400 点
問題文
すぬけ君はある日友人から長さ N の順列 a_1, a_2, ..., a_N を貰いました。
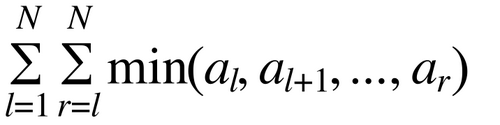
を求めてください。
制約
- 1 ≦ N ≦ 200,000
- (a_1, a_2, ..., a_N) は (1, 2, ..., N) を並び替えたものである
入力
入力は以下の形式で標準入力から与えられる。
N a_1 a_2 ... a_N
出力
1 行に答えを出力する。
なお、32bit整数型に答えが収まるとは限らないことに注意すること。
入力例 1
3 2 1 3
出力例 1
9
入力例 2
4 1 3 2 4
出力例 2
19
入力例 3
8 5 4 8 1 2 6 7 3
出力例 3
85
Score : 400 points
Problem Statement
One day, Snuke was given a permutation of length N, a_1, a_2, ..., a_N, from his friend.
Find the following:
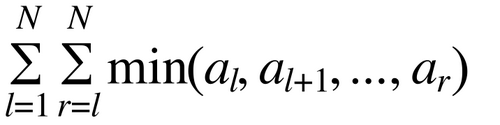
Constraints
- 1 ≦ N ≦ 200,000
- (a_1, a_2, ..., a_N) is a permutation of (1, 2, ..., N).
Input
The input is given from Standard Input in the following format:
N a_1 a_2 ... a_N
Output
Print the answer.
Note that the answer may not fit into a 32-bit integer.
Sample Input 1
3 2 1 3
Sample Output 1
9
Sample Input 2
4 1 3 2 4
Sample Output 2
19
Sample Input 3
8 5 4 8 1 2 6 7 3
Sample Output 3
85
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 700 点
問題文
青木君は数列と木が大好きです。
青木君はある日高橋くんから長さ N の数列 a_1, a_2, ..., a_N を貰いました。そしてこの数列を見て、木を作りたくなりました。
青木君が作りたいのは、頂点数が N で、全ての i = 1,2,...,N について頂点 i と最も遠い頂点の距離が a_i となる木です。なお、辺の長さは全て 1 とします。
これを満たす木が存在するか判定してください。
制約
- 2 ≦ N ≦ 100
- 1 ≦ a_i ≦ N-1
入力
入力は以下の形式で標準入力から与えられる。
N a_1 a_2 ... a_N
出力
条件を満たす木が存在するならば Possible、しないならば Impossible と出力する。
入力例 1
5 3 2 2 3 3
出力例 1
Possible
上図は条件を見たす木の一例です。赤い矢印は最も遠い頂点への経路を表します。
入力例 2
3 1 1 2
出力例 2
Impossible
入力例 3
10 1 2 2 2 2 2 2 2 2 2
出力例 3
Possible
入力例 4
10 1 1 2 2 2 2 2 2 2 2
出力例 4
Impossible
入力例 5
6 1 1 1 1 1 5
出力例 5
Impossible
入力例 6
5 4 3 2 3 4
出力例 6
Possible
Score : 700 points
Problem Statement
Aoki loves numerical sequences and trees.
One day, Takahashi gave him an integer sequence of length N, a_1, a_2, ..., a_N, which made him want to construct a tree.
Aoki wants to construct a tree with N vertices numbered 1 through N, such that for each i = 1,2,...,N, the distance between vertex i and the farthest vertex from it is a_i, assuming that the length of each edge is 1.
Determine whether such a tree exists.
Constraints
- 2 ≦ N ≦ 100
- 1 ≦ a_i ≦ N-1
Input
The input is given from Standard Input in the following format:
N a_1 a_2 ... a_N
Output
If there exists a tree that satisfies the condition, print Possible. Otherwise, print Impossible.
Sample Input 1
5 3 2 2 3 3
Sample Output 1
Possible

The diagram above shows an example of a tree that satisfies the conditions. The red arrows show paths from each vertex to the farthest vertex from it.
Sample Input 2
3 1 1 2
Sample Output 2
Impossible
Sample Input 3
10 1 2 2 2 2 2 2 2 2 2
Sample Output 3
Possible
Sample Input 4
10 1 1 2 2 2 2 2 2 2 2
Sample Output 4
Impossible
Sample Input 5
6 1 1 1 1 1 5
Sample Output 5
Impossible
Sample Input 6
5 4 3 2 3 4
Sample Output 6
Possible
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 900 点
問題文
すぬけ君は順列が大好きなので、長さ N の順列を作ることにしました。
ただしすぬけ君は整数 K が嫌いなので、以下の条件を満たす順列を作ることにしました。
- 順列を a_1, a_2, ..., a_N とする。全ての i = 1,2,...,N について、|a_i - i| \neq K を満たす
長さ N の順列は N! 通りありますが、そのうち条件をみたすものは何個あるかを求めてください。
ただし答えは非常に大きくなることがあるので、答えを 924844033(素数) で割ったあまりを求めてください。
制約
- 2 ≦ N ≦ 2000
- 1 ≦ K ≦ N-1
入力
入力は以下の形式で標準入力から与えられる。
N K
出力
1 行に答えを 924844033 で割ったあまりを出力する。
入力例 1
3 1
出力例 1
2
(1, 2, 3), (3, 2, 1) の 2 つが条件を満たす。
入力例 2
4 1
出力例 2
5
(1, 2, 3, 4), (1, 4, 3, 2), (3, 2, 1, 4), (3, 4, 1, 2), (4, 2, 3, 1) の 5 つが条件を満たす。
入力例 3
4 2
出力例 3
9
入力例 4
4 3
出力例 4
14
入力例 5
425 48
出力例 5
756765083
Score : 900 points
Problem Statement
Snuke loves permutations. He is making a permutation of length N.
Since he hates the integer K, his permutation will satisfy the following:
- Let the permutation be a_1, a_2, ..., a_N. For each i = 1,2,...,N, |a_i - i| \neq K.
Among the N! permutations of length N, how many satisfies this condition?
Since the answer may be extremely large, find the answer modulo 924844033(prime).
Constraints
- 2 ≦ N ≦ 2000
- 1 ≦ K ≦ N-1
Input
The input is given from Standard Input in the following format:
N K
Output
Print the answer modulo 924844033.
Sample Input 1
3 1
Sample Output 1
2
2 permutations (1, 2, 3), (3, 2, 1) satisfy the condition.
Sample Input 2
4 1
Sample Output 2
5
5 permutations (1, 2, 3, 4), (1, 4, 3, 2), (3, 2, 1, 4), (3, 4, 1, 2), (4, 2, 3, 1) satisfy the condition.
Sample Input 3
4 2
Sample Output 3
9
Sample Input 4
4 3
Sample Output 4
14
Sample Input 5
425 48
Sample Output 5
756765083
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1400 点
問題文
しぐま君とすぎむ君はゲームをすることにしました。
このゲームは N 頂点のグラフの上で行います。頂点には 1,2,...,N と番号がついています。グラフには N-1 本の赤い辺と N-1 本の青い辺があり、どちらも木となっています。赤い辺は (a_i, b_i) で表し、青い辺は (c_i, d_i) で表します。
二人はそれぞれ駒を 1 個ずつ持っており、しぐま君の駒の初期位置は頂点 X、すぎむ君の駒の初期位置は頂点 Y です。
このゲームはターン制で、ターン 1, ターン 2, ターン 3, ... と進んでいきます。そして、ターン 1, 3, 5, ... はしぐま君、ターン 2, 4, 6, ... はすぎむ君の手番です。
二人は自分の手番では、自分の駒を動かすかパスをします。ただし動かせる頂点には制限があり、しぐま君は赤い辺、すぎむ君は青い辺で隣り合った頂点のみに駒を動かせます。
もし二つの駒が同じ頂点に来るとその時点でゲームは終了します。そしてターン i での操作の後にゲームが終了したならば、i を総ターン数とします。
しぐま君は総ターン数を出来る限り大きく、すぎむ君は出来る限り小さくしたいです。
二人はこの目的のもとで最適に行動をすると仮定したとき、ゲームは終了するかを判定し、終了する場合は総ターン数はいくつになるか求めてください。
制約
- 2 ≦ N ≦ 200,000
- 1 ≦ X, Y ≦ N
- X \neq Y
- 1 ≦ a_i, b_i, c_i, d_i ≦ N
- 赤い辺と青い辺はそれぞれ木である
入力
入力は以下の形式で標準入力から与えられる。
N X Y
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
c_1 d_1
c_2 d_2
:
c_{N-1} d_{N-1}
出力
1 行に答えを出力する。
ただし、いつまでもゲームが終了しない場合は -1 を出力する。
入力例 1
4 1 2 1 2 1 3 1 4 2 1 2 3 1 4
出力例 1
4
入力例 2
3 3 1 1 2 2 3 1 2 2 3
出力例 2
4
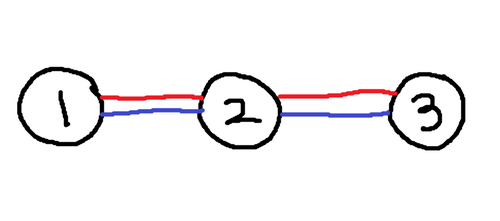
入力例 3
4 1 2 1 2 3 4 2 4 1 2 3 4 1 3
出力例 3
2
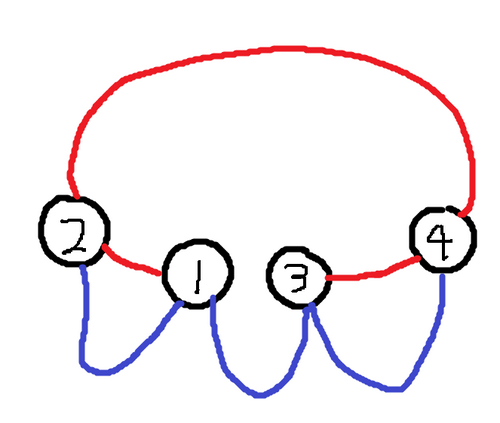
入力例 4
4 2 1 1 2 3 4 2 4 1 2 3 4 1 3
出力例 4
-1
入力例 5
5 1 2 1 2 1 3 1 4 4 5 2 1 1 3 1 5 5 4
出力例 5
6
Score : 1400 points
Problem Statement
Sigma and Sugim are playing a game.
The game is played on a graph with N vertices numbered 1 through N. The graph has N-1 red edges and N-1 blue edges, and the N-1 edges in each color forms a tree. The red edges are represented by pairs of integers (a_i, b_i), and the blue edges are represented by pairs of integers (c_i, d_i).
Each player has his own piece. Initially, Sigma's piece is at vertex X, and Sugim's piece is at vertex Y.
The game is played in turns, where turns are numbered starting from turn 1. Sigma takes turns 1, 3, 5, ..., and Sugim takes turns 2, 4, 6, ....
In each turn, the current player either moves his piece, or does nothing. Here, Sigma can only move his piece to a vertex that is directly connected to the current vertex by a red edge. Similarly, Sugim can only move his piece to a vertex that is directly connected to the current vertex by a blue edge.
When the two pieces come to the same vertex, the game ends immediately. If the game ends just after the operation in turn i, let i be the total number of turns in the game.
Sigma's objective is to make the total number of turns as large as possible, while Sugim's objective is to make it as small as possible.
Determine whether the game will end in a finite number of turns, assuming both players plays optimally to achieve their respective objectives. If the answer is positive, find the number of turns in the game.
Constraints
- 2 ≦ N ≦ 200,000
- 1 ≦ X, Y ≦ N
- X \neq Y
- 1 ≦ a_i, b_i, c_i, d_i ≦ N
- The N-1 edges in each color (red and blue) forms a tree.
Input
The input is given from Standard Input in the following format:
N X Y
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
c_1 d_1
c_2 d_2
:
c_{N-1} d_{N-1}
Output
If the game will end in a finite number of turns, print the number of turns.
Otherwise, print -1.
Sample Input 1
4 1 2 1 2 1 3 1 4 2 1 2 3 1 4
Sample Output 1
4

Sample Input 2
3 3 1 1 2 2 3 1 2 2 3
Sample Output 2
4

Sample Input 3
4 1 2 1 2 3 4 2 4 1 2 3 4 1 3
Sample Output 3
2

Sample Input 4
4 2 1 1 2 3 4 2 4 1 2 3 4 1 3
Sample Output 4
-1
Sample Input 5
5 1 2 1 2 1 3 1 4 4 5 2 1 1 3 1 5 5 4
Sample Output 5
6
実行時間制限: 5 sec / メモリ制限: 512 MiB
配点 : 1900 点
問題文
高橋君はある日青木君から以下の様な問題を貰いました。
- N 頂点の木と、整数 K が与えられる。木の頂点は 1,2,...,N と番号がついているものとし、辺は (a_i, b_i) で表す。
- 頂点の集合 S について f(S) を、S をすべて含む部分木の頂点数の最小値とする
- 木から K 個の頂点を選ぶ方法は _NC_K 通りあるが、それぞれについて選んだ頂点を S とし、 f(S) の総和を求める
- 答えは大きくなることがあるので、924844033(素数) で割ったあまりを出力する
高橋君にとってこの問題は簡単すぎました。なので K = 1,2,...,N 全てについてこの問題を解くことにしました。
制約
- 2 ≦ N ≦ 200,000
- 1 ≦ a_i, b_i ≦ N
- 与えられるグラフは木である
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
出力
N 行出力する。i 行目には、K=i の時の問題の答えを 924844033 で割ったあまりを出力する。
入力例 1
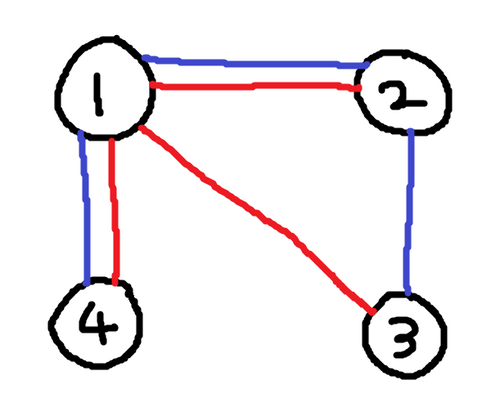
3 1 2 2 3
出力例 1
3 7 3
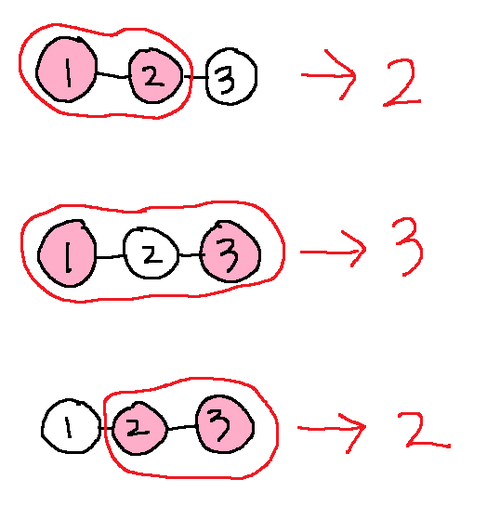
上図は、K=2 の場合を図示している。ピンク色の頂点が選んだ頂点で、赤く囲われたのが頂点数最小の部分木である。
入力例 2
4 1 2 1 3 1 4
出力例 2
4 15 13 4
入力例 3
7 1 2 2 3 2 4 4 5 4 6 6 7
出力例 3
7 67 150 179 122 45 7
Score : 1900 points
Problem Statement
One day, Takahashi was given the following problem from Aoki:
- You are given a tree with N vertices and an integer K. The vertices are numbered 1 through N. The edges are represented by pairs of integers (a_i, b_i).
- For a set S of vertices in the tree, let f(S) be the minimum number of the vertices in a subtree of the given tree that contains all vertices in S.
- There are
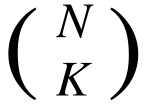 ways to choose K vertices from the trees. For each of them, let S be the set of the chosen vertices, and find the sum of f(S) over all
ways to choose K vertices from the trees. For each of them, let S be the set of the chosen vertices, and find the sum of f(S) over all 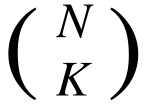 ways.
ways. - Since the answer may be extremely large, print it modulo 924844033(prime).
Since it was too easy for him, he decided to solve this problem for all K = 1,2,...,N.
Constraints
- 2 ≦ N ≦ 200,000
- 1 ≦ a_i, b_i ≦ N
- The given graph is a tree.
Input
The input is given from Standard Input in the following format:
N
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
Output
Print N lines. The i-th line should contain the answer to the problem where K=i, modulo 924844033.
Sample Input 1
3 1 2 2 3
Sample Output 1
3 7 3

The diagram above illustrates the case where K=2. The chosen vertices are colored pink, and the subtrees with the minimum number of vertices are enclosed by red lines.
Sample Input 2
4 1 2 1 3 1 4
Sample Output 2
4 15 13 4
Sample Input 3
7 1 2 2 3 2 4 4 5 4 6 6 7
Sample Output 3
7 67 150 179 122 45 7