Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
高橋君には N 人の友達がいます。N 人の友達はそれぞれ、友達 1 、友達 2 、\ldots 、友達 N というあだ名で呼ばれています。
ある日、高橋君はある恥ずかしい秘密を、友達の一人である友達 X に知られてしまいました。
i = 1, 2, \ldots, N について、友達 i が高橋君の秘密を知ったとき、友達 A_i がまだ高橋君の秘密を知らなければ、友達 i は高橋君の秘密を友達 A_i にも教えてしまいます。
高橋君の秘密は最終的に何人の友達に知られることになるでしょうか?
制約
- 2 \leq N \leq 10^5
- 1 \leq X \leq N
- 1 \leq A_i \leq N
- A_i \neq i
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N X A_1 A_2 \cdots A_N
出力
答えを出力せよ。
入力例 1
4 2 3 1 1 2
出力例 1
3
高橋君の秘密は以下の流れで友達 1 、友達 2 、友達 3 の 3 人に知れ渡ります。
- ある日、高橋君は秘密を友達 2 に知られてしまいました。
- 秘密を知った友達 2 は、その秘密を友達 1 に教えます。
- 秘密を知った友達 1 は、その秘密を友達 3 に教えます。
高橋君の秘密は最終的に 3 人の友達に知られることになるため、3 を出力します。
入力例 2
20 12 7 11 10 1 7 20 14 2 17 3 2 5 19 20 8 14 18 2 10 10
出力例 2
7
Score : 200 points
Problem Statement
Takahashi has N friends. They have nicknames: Friend 1, Friend 2, \ldots, Friend N.
One day, Takahashi accidentally let one of his friends, Friend X, learn his shameful secret.
For each i = 1, 2, \ldots, N, when Friend i learns the secret, he/she will share it with Friend A_i, if Friend A_i has not already learned it.
How many of Takahashi's friends will learn the secret in the end?
Constraints
- 2 \leq N \leq 10^5
- 1 \leq X \leq N
- 1 \leq A_i \leq N
- A_i \neq i
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N X A_1 A_2 \cdots A_N
Output
Print the answer.
Sample Input 1
4 2 3 1 1 2
Sample Output 1
3
Takahashi's secret will be learned by Friend 1, Friend 2, and Friend 3, as follows.
- One day, Takahashi let Friend 2 learn the secret.
- Friend 2 shares it with Friend 1.
- Friend 1 shares it with Friend 3.
In the end, three of his friends learn the secret, so we print 3.
Sample Input 2
20 12 7 11 10 1 7 20 14 2 17 3 2 5 19 20 8 14 18 2 10 10
Sample Output 2
7
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
縦 H 行横 W 列のマス目があります。上から i 行目、左から j 列目のマスをマス (i,j) と表します。
マス (i,j) は S_{i,j} が # のとき通行不可能、. のとき通行可能であり家が建っていない、@ のとき通行可能であり家が建っていることを表します。
最初、マス (X,Y) にサンタクロースがいます。サンタクロースは文字列 T に従って以下の行動を行います。
- 文字列 T の長さを |T| とする。i=1,2,\ldots,|T| の順に以下のように移動する。
- 現在サンタクロースがいるマスを (x,y) とする。
- T_i が
Uかつマス (x-1,y) が通行可能ならマス (x-1,y) に移動する。 - T_i が
Dかつマス (x+1,y) が通行可能ならマス (x+1,y) に移動する。 - T_i が
Lかつマス (x,y-1) が通行可能ならマス (x,y-1) に移動する。 - T_i が
Rかつマス (x,y+1) が通行可能ならマス (x,y+1) に移動する。 - それ以外の場合、マス (x,y) に留まる。
- T_i が
- 現在サンタクロースがいるマスを (x,y) とする。
行動を終えたあとにサンタクロースがいるマスと、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。
制約
- 3 \leq H,W \leq 100
- 1 \leq X \leq H
- 1 \leq Y \leq W
- 与えられる数値は全て整数である
- S_{i,j} は
#,.,@のいずれか - 全ての 1 \leq i \leq H について S_{i,1},S_{i,W} は
# - 全ての 1 \leq j \leq W について S_{1,j},S_{H,j} は
# - S_{X,Y}=
. - T は
U,D,L,Rのいずれかからなる長さ 1 以上 10^4 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
H W X Y
S_{1,1}S_{1,2}\ldots S_{1,W}
\dots
S_{H,1}S_{H,2}\ldots S_{H,W}
T
出力
行動を終えたあとサンタクロースがいるマスを (X,Y)、行動により通過または到達した家の数を C とするとき、X,Y,C をこの順に空白区切りで出力せよ。
入力例 1
5 5 3 4 ##### #...# #.@.# #..@# ##### LLLDRUU
出力例 1
2 3 1
サンタクロースは以下のように行動します。
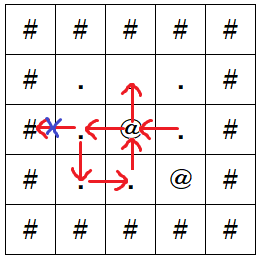
- T_1=
Lなのでマス (3,4) からマス (3,3) に移動する。これにより家を通過する。 - T_2=
Lなのでマス (3,3) からマス (3,2) に移動する。 - T_3=
Lだがマス (3,1) は通行不可能なので、マス (3,2) に留まる。 - T_4=
Dなのでマス (3,2) からマス (4,2) に移動する。 - T_5=
Rなのでマス (4,2) からマス (4,3) に移動する。 - T_6=
Uなのでマス (4,3) からマス (3,3) に移動する。これにより家を通過するが、この家はすでに通過したことがある家である。 - T_7=
Uなのでマス (3,3) からマス (2,3) に移動する。
行動により通過または到達した家の数は 1 です。
入力例 2
6 13 4 6 ############# #@@@@@@@@@@@# #@@@@@@@@@@@# #@@@@.@@@@@@# #@@@@@@@@@@@# ############# UURUURLRLUUDDURDURRR
出力例 2
3 11 11
入力例 3
12 35 7 10 ################################### #.................................# #..........@......................# #......@................@.........# #.............##............@.....# #...##........##....##............# #...##........##....##.......##...# #....##......##......##....##.....# #....##......##......##..##.......# #.....#######.........###.........# #.................................# ################################### LRURRRUUDDULUDUUDLRLRDRRLULRRUDLDRU
出力例 3
4 14 1
Score : 200 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
If S_{i,j} is #, the cell (i,j) is impassable; if it is ., the cell is passable and contains no house; if it is @, the cell is passable and contains a house.
Initially, Santa Claus is in cell (X,Y). He will act according to the string T as follows.
- Let |T| be the length of the string T. For i=1,2,\ldots,|T|, he moves as follows.
- Let (x,y) be the cell he is currently in.
- If T_i is
Uand cell (x-1,y) is passable, move to cell (x-1,y). - If T_i is
Dand cell (x+1,y) is passable, move to cell (x+1,y). - If T_i is
Land cell (x,y-1) is passable, move to cell (x,y-1). - If T_i is
Rand cell (x,y+1) is passable, move to cell (x,y+1). - Otherwise, stay in cell (x,y).
- If T_i is
- Let (x,y) be the cell he is currently in.
Find the cell where he is after completing all actions, and the number of distinct houses that he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.
Constraints
- 3 \leq H,W \leq 100
- 1 \leq X \leq H
- 1 \leq Y \leq W
- All given numbers are integers.
- Each S_{i,j} is one of
#,.,@. - S_{i,1} and S_{i,W} are
#for every 1 \leq i \leq H. - S_{1,j} and S_{H,j} are
#for every 1 \leq j \leq W. - S_{X,Y}=
. - T is a string of length at least 1 and at most 10^4, consisting of
U,D,L,R.
Input
The Input is given from Standard Input in the following format:
H W X Y
S_{1,1}S_{1,2}\ldots S_{1,W}
\dots
S_{H,1}S_{H,2}\ldots S_{H,W}
T
Output
Let (X,Y) be the cell where he is after completing all actions, and C be the number of distinct houses he passed through or arrived at during his actions. Print X,Y,C in this order separated by spaces.
Sample Input 1
5 5 3 4 ##### #...# #.@.# #..@# ##### LLLDRUU
Sample Output 1
2 3 1
Santa Claus behaves as follows:

- T_1=
L, so he moves from (3,4) to (3,3). A house is passed. - T_2=
L, so he moves from (3,3) to (3,2). - T_3=
L, but cell (3,1) is impassable, so he stays at (3,2). - T_4=
D, so he moves from (3,2) to (4,2). - T_5=
R, so he moves from (4,2) to (4,3). - T_6=
U, so he moves from (4,3) to (3,3). A house is passed, but it has already been passed. - T_7=
U, so he moves from (3,3) to (2,3).
The number of houses he passed or arrived during his actions is 1.
Sample Input 2
6 13 4 6 ############# #@@@@@@@@@@@# #@@@@@@@@@@@# #@@@@.@@@@@@# #@@@@@@@@@@@# ############# UURUURLRLUUDDURDURRR
Sample Output 2
3 11 11
Sample Input 3
12 35 7 10 ################################### #.................................# #..........@......................# #......@................@.........# #.............##............@.....# #...##........##....##............# #...##........##....##.......##...# #....##......##......##....##.....# #....##......##......##..##.......# #.....#######.........###.........# #.................................# ################################### LRURRRUUDDULUDUUDLRLRDRRLULRRUDLDRU
Sample Output 3
4 14 1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 250 点
問題文
1 から N の番号がついた N 個の箱と 1 から N の番号がついた N 個の荷物があります。荷物 i (1 \leq i \leq N) は箱 A_i の中にあり、重さは W_i です。
あなたは荷物を一つ選び、他の箱の中に移動させる操作を 0 回以上繰り返し行うことができます。1 回の操作で移動させる荷物の重さが w であるとき、w のコストがかかります。
全ての箱に荷物が 1 つずつ入っている状態にするためにかかるコストの総和の最小値を求めてください。
制約
- 1 \leq N \leq 10^{5}
- 1 \leq A_i \leq N (1 \leq i \leq N)
- 1 \leq W_i \leq 10^{4} (1 \leq i \leq N)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N W_1 W_2 \ldots W_N
出力
全ての箱に荷物が 1 つずつ入っている状態にするためにかかるコストの総和の最小値を出力せよ。
入力例 1
5 2 2 3 3 5 33 40 2 12 16
出力例 1
35
以下の 2 回の荷物の移動で、すべての箱に荷物が 1 つずつ入っている状態にすることができます。
- 荷物 1 を箱 2 から箱 1 に移す。このとき、コストは 33 である。
- 荷物 3 を箱 3 から箱 4 に移す。このとき、コストは 2 である。
この 2 回の荷物の移動は合計 35 のコストかかります。 35 未満のコストですべての箱に荷物が 1 つずつ入っている状態にすることはできないため、 35 を出力します。
入力例 2
12 3 6 7 4 12 4 8 11 11 1 8 11 3925 9785 9752 3587 4013 1117 3937 7045 6437 6208 3391 6309
出力例 2
17254
Score : 250 points
Problem Statement
There are N boxes numbered 1 to N and N items numbered 1 to N. Item i (1 \leq i \leq N) is in box A_i and has a weight of W_i.
You can repeatedly perform the operation of choosing an item and moving it to another box zero or more times. If the weight of the item being moved is w, the cost of the operation is w.
Find the minimum total cost required to make each box contain exactly one item.
Constraints
- 1 \leq N \leq 10^{5}
- 1 \leq A_i \leq N (1 \leq i \leq N)
- 1 \leq W_i \leq 10^{4} (1 \leq i \leq N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N W_1 W_2 \ldots W_N
Output
Print the minimum total cost required to make each box contain exactly one item.
Sample Input 1
5 2 2 3 3 5 33 40 2 12 16
Sample Output 1
35
With the following two moves, you can make each box contain exactly one item:
- Move item 1 from box 2 to box 1. The cost is 33.
- Move item 3 from box 3 to box 4. The cost is 2.
The total cost of these two moves is 35. It is impossible to make each box contain exactly one item with a cost less than 35, so print 35.
Sample Input 2
12 3 6 7 4 12 4 8 11 11 1 8 11 3925 9785 9752 3587 4013 1117 3937 7045 6437 6208 3391 6309
Sample Output 2
17254
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
10^{100} 行 7 列の行列 A があり、任意の整数対 (i,j)\ (1 \leq i \leq 10^{100}, 1 \leq j \leq 7) についてその (i,j) 成分は (i-1) \times 7 + j です。
N 行 M 列の行列 B が与えられるので、B が A から一部の矩形領域を(向きを変えずに)切り出したものであるかを判定してください。
制約
- 1 \leq N \leq 10^4
- 1 \leq M \leq 7
- 1 \leq B_{i,j} \leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M
B_{1,1} B_{1,2} \ldots B_{1,M}
B_{2,1} B_{2,2} \ldots B_{2,M}
\hspace{1.6cm}\vdots
B_{N,1} B_{N,2} \ldots B_{N,M}
出力
B が A から一部の矩形領域を切り出したものであれば Yes と、そうでないなら No と出力せよ。
入力例 1
2 3 1 2 3 8 9 10
出力例 1
Yes
与えられる B は、A の左上 2 行 3 列を切り出したものとなっています。
入力例 2
2 1 1 2
出力例 2
No
与えられる B を 90 度回転させると A の左上 1 行 2 列と一致しますが、問題文中に「向きを変えずに」とある通り回転による一致は認められていないため、答えは No となります。
入力例 3
10 4 1346 1347 1348 1349 1353 1354 1355 1356 1360 1361 1362 1363 1367 1368 1369 1370 1374 1375 1376 1377 1381 1382 1383 1384 1388 1389 1390 1391 1395 1396 1397 1398 1402 1403 1404 1405 1409 1410 1411 1412
出力例 3
Yes
Score : 300 points
Problem Statement
There is a 10^{100} \times 7 matrix A, where the (i,j)-th entry is (i-1) \times 7 + j for every pair of integers (i,j)\ (1 \leq i \leq 10^{100}, 1 \leq j \leq 7).
Given an N \times M matrix B, determine whether B is some (unrotated) rectangular part of A.
Constraints
- 1 \leq N \leq 10^4
- 1 \leq M \leq 7
- 1 \leq B_{i,j} \leq 10^9
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N M
B_{1,1} B_{1,2} \ldots B_{1,M}
B_{2,1} B_{2,2} \ldots B_{2,M}
\hspace{1.6cm}\vdots
B_{N,1} B_{N,2} \ldots B_{N,M}
Output
If B is some rectangular part of A, print Yes; otherwise, print No.
Sample Input 1
2 3 1 2 3 8 9 10
Sample Output 1
Yes
The given matrix B is the top-left 2 \times 3 submatrix of A.
Sample Input 2
2 1 1 2
Sample Output 2
No
Although the given matrix B would match the top-left 1 \times 2 submatrix of A after rotating 90 degrees, the Problem Statement asks whether B is an unrotated part of A, so the answer is No.
Sample Input 3
10 4 1346 1347 1348 1349 1353 1354 1355 1356 1360 1361 1362 1363 1367 1368 1369 1370 1374 1375 1376 1377 1381 1382 1383 1384 1388 1389 1390 1391 1395 1396 1397 1398 1402 1403 1404 1405 1409 1410 1411 1412
Sample Output 3
Yes
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
AtCoder 国には動物園が N 園あり、1 から N の番号がついています。動物園 i の入園料は C_i 円です。
鈴木さんは M 種類の動物、動物 1,\ldots,M が好きです。
動物 i は K_i 園の動物園 A_{i,1},\dots, A_{i,K_i} で見ることができます。
M 種類の動物全てを 2 度以上ずつ見るために必要な入園料の合計の最小値を求めてください。
なお、同じ動物園を複数回訪れた場合、その動物園の動物は訪れた回数だけ見たとみなします。
制約
- 1\leq N \leq 10
- 1\leq M \leq 100
- 0\leq C_i \leq 10^9
- 1\leq K_i \leq N
- 1 \leq A_{i,j} \leq N
- j \neq j' \Longrightarrow A_{i,j}\neq A_{i,j'}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M
C_1 \dots C_N
K_1 A_{1,1} \dots A_{1,K_1}
\vdots
K_M A_{M,1} \dots A_{M,K_M}
出力
答えを出力せよ。
入力例 1
4 3 1000 300 700 200 3 1 3 4 3 1 2 4 2 1 3
出力例 1
1800
以下のようにすることで、1800 円で動物 1,2,3 を 2 度以上ずつ見ることができます。
- 動物園 3 に行く。入園料 700 円を払い、動物 1,3 を見る。
- 動物園 3 に行く。入園料 700 円を払い、動物 1,3 を見る。
- 動物園 4 に行く。入園料 200 円を払い、動物 1,2 を見る。
- 動物園 4 に行く。入園料 200 円を払い、動物 1,2 を見る。
入力例 2
7 6 500 500 500 500 500 500 1000 3 1 2 7 3 2 3 7 3 3 4 7 3 4 5 7 3 5 6 7 3 6 1 7
出力例 2
2000
動物園 7 に 2 度行くことで、合計 2000 円で動物 1,2,3,4,5,6 を 2 度ずつ見ることができます。
Score : 400 points
Problem Statement
In the country of AtCoder there are N zoos, numbered 1 to N. The admission fee for zoo i is C_i yen.
Mr. Suzuki likes M kinds of animals, animals 1,\dots,M.
Animal i can be seen at K_i zoos, namely zoos A_{i,1},\dots,A_{i,K_i}.
Find the minimum total admission fee required to see all M kinds of animals at least twice each.
If you visit the same zoo multiple times, the animals there are considered seen once per every visit.
Constraints
- 1 \le N \le 10
- 1 \le M \le 100
- 0 \le C_i \le 10^9
- 1 \le K_i \le N
- 1 \le A_{i,j} \le N
- j \neq j' \Longrightarrow A_{i,j} \neq A_{i,j'}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M
C_1 \dots C_N
K_1 A_{1,1} \dots A_{1,K_1}
\vdots
K_M A_{M,1} \dots A_{M,K_M}
Output
Output the minimum total admission fee.
Sample Input 1
4 3 1000 300 700 200 3 1 3 4 3 1 2 4 2 1 3
Sample Output 1
1800
For example, the following schedule achieves seeing animals 1,2,3 at least twice each for a total of 1800 yen:
- Go to zoo 3. Pay 700 yen and see animals 1 and 3.
- Go to zoo 3. Pay 700 yen and see animals 1 and 3.
- Go to zoo 4. Pay 200 yen and see animals 1 and 2.
- Go to zoo 4. Pay 200 yen and see animals 1 and 2.
Sample Input 2
7 6 500 500 500 500 500 500 1000 3 1 2 7 3 2 3 7 3 3 4 7 3 4 5 7 3 5 6 7 3 6 1 7
Sample Output 2
2000
By visiting zoo 7 twice, you can see animals 1,2,3,4,5,6 twice each for a total of 2000 yen.