Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
ここに円形のピザが 1 枚あります。
高橋くんは長さ N の数列 A を使ってこのピザを以下の手順で切り分けます。
- 最初に、円の中心から 12 時の方向に切れ込みをひとつ入れます。
- 次に、以下の操作を N 回繰り返します。 i 回目の操作では以下を行います。
- まず、ピザを時計回りに A_i 度回転させる。
- 次に、円の中心から 12 時の方向に切れ込みをひとつ入れる。
例えば、A=(90,180,45,195) として手順を行うと、下図のようになります。

このとき、最も大きなピザの中心角が何度であるか求めてください。
制約
- 入力は全て整数
- 1 \le N \le 359
- 1 \le A_i \le 359
- 同じ場所に複数回切れ込みが入ることはない。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \dots A_N
出力
答えを整数として出力せよ。
入力例 1
4 90 180 45 195
出力例 1
120
この入力は問題文中の例と一致します。
最も大きなピザの中心角は 120 度です。
入力例 2
1 1
出力例 2
359
入力例 3
10 215 137 320 339 341 41 44 18 241 149
出力例 3
170
Score : 200 points
Problem Statement
We have a circular pizza.
Takahashi will cut this pizza using a sequence A of length N, according to the following procedure.
- First, make a cut from the center in the 12 o'clock direction.
- Next, do N operations. The i-th operation is as follows.
- Rotate the pizza A_i degrees clockwise.
- Then, make a cut from the center in the 12 o'clock direction.
For example, if A=(90,180,45,195), the procedure cuts the pizza as follows.

Find the center angle of the largest pizza after the procedure.
Constraints
- All values in input are integers.
- 1 \le N \le 359
- 1 \le A_i \le 359
- There will be no multiple cuts at the same position.
Input
Input is given from Standard Input in the following format:
N A_1 A_2 \dots A_N
Output
Print the answer as an integer.
Sample Input 1
4 90 180 45 195
Sample Output 1
120
This input coincides with the example in the Problem Statement.
The center angle of the largest pizza is 120 degrees.
Sample Input 2
1 1
Sample Output 2
359
Sample Input 3
10 215 137 320 339 341 41 44 18 241 149
Sample Output 3
170
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
1 から N までの番号がついた N 人の参加者が、1 から M までの番号がついた M 問からなるコンテストに参加します。
1 以上 N 以下の整数 i 、1 以上 M 以下の整数 j について、S_i の j 番目の文字が o のとき参加者 i は問題 j を解くことが可能で、S_i の j 番目の文字が x のとき参加者 i は問題 j を解くことが不可能です。
このコンテストは、二人の参加者でペアを組んで参加します。二人が協力することで M 問全てを解くことが可能であるようなペアの個数を答えてください。
より厳密には、1\leq x < y\leq N を満たす整数の組 (x,y) であって、 1 以上 M 以下の任意の整数 j について、参加者 x か参加者 y の少なくとも一方は問題 j を解くことが可能であるという条件を満たすものの個数を答えてください。
制約
- N は 2 以上 30 以下の整数
- M は 1 以上 30 以下の整数
- S_i は
o,xからなる長さ M の文字列
入力
入力は以下の形式で標準入力から与えられる。
N M S_1 S_2 \vdots S_N
出力
答えを出力せよ。
入力例 1
5 5 ooooo oooxx xxooo oxoxo xxxxx
出力例 1
5
参加者 1 と 2 のペア、参加者 1 と 3 のペア、参加者 1 と 4 のペア、参加者 1 と 5 のペア、参加者 2 と 3 のペアの 5 個のペアが条件を満たします。
例えば参加者 2 と 4 のペアは、問題 4 が解けないので条件を満たしません。
入力例 2
3 2 ox xo xx
出力例 2
1
入力例 3
2 4 xxxx oxox
出力例 3
0
Score : 200 points
Problem Statement
N participants, numbered 1 to N, will participate in a contest with M problems, numbered 1 to M.
For an integer i between 1 and N and an integer j between 1 and M, participant i can solve problem j if the j-th character of S_i is o, and cannot solve it if that character is x.
The participants must be in pairs. Print the number of ways to form a pair of participants who can collectively solve all the M problems.
More formally, print the number of pairs (x,y) of integers satisfying 1\leq x < y\leq N such that for any integer j between 1 and M, at least one of participant x and participant y can solve problem j.
Constraints
- N is an integer between 2 and 30, inclusive.
- M is an integer between 1 and 30, inclusive.
- S_i is a string of length M consisting of
oandx.
Input
The input is given from Standard Input in the following format:
N M S_1 S_2 \vdots S_N
Output
Print the answer.
Sample Input 1
5 5 ooooo oooxx xxooo oxoxo xxxxx
Sample Output 1
5
The following five pairs satisfy the condition: participants 1 and 2, participants 1 and 3, participants 1 and 4, participants 1 and 5, and participants 2 and 3.
On the other hand, the pair of participants 2 and 4, for instance, does not satisfy the condition because they cannot solve problem 4.
Sample Input 2
3 2 ox xo xx
Sample Output 2
1
Sample Input 3
2 4 xxxx oxox
Sample Output 3
0
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
長さ N の非負整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
A の異なる 2 要素の和として表せる値の中に偶数が存在するか判定し、存在する場合その最大値を求めてください。
制約
- 2\leq N \leq 2\times 10^5
- 0\leq A_i\leq 10^9
- A の要素は相異なる
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
A の異なる 2 要素の和として表せる値の中に偶数が存在しない場合、-1 を出力せよ。
偶数が存在する場合、その最大値を出力せよ。
入力例 1
3 2 3 4
出力例 1
6
A の異なる 2 要素の和として表せる値は 5,6,7 です。この中に偶数は存在し、その最大値は 6 です。
入力例 2
2 1 0
出力例 2
-1
A の異なる 2 要素の和として表せる値は 1 です。この中に偶数は存在しないので、 -1 を出力してください。
Score : 300 points
Problem Statement
You are given a sequence A=(A_1,A_2,\ldots,A_N) of length N consisting of non-negative integers.
Determine if there is an even number represented as the sum of two different elements of A. If it exists, find the maximum such number.
Constraints
- 2\leq N \leq 2\times 10^5
- 0\leq A_i\leq 10^9
- The elements of A are distinct.
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Print -1 if there is no even number represented as the sum of two different elements of A.
If such an even number exists, print the maximum such number.
Sample Input 1
3 2 3 4
Sample Output 1
6
The values represented as the sum of two distinct elements of A are 5, 6, and 7. We have an even number here, and the maximum is 6.
Sample Input 2
2 1 0
Sample Output 2
-1
The value represented as the sum of two distinct elements of A is 1. We have no even number here, so -1 should be printed.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
頂点 1, 頂点 2,\ldots, 頂点 N の N 個の頂点からなる単純無向グラフ G,H が与えられます。 G には M _ G 本の辺があり、i 本目 (1\leq i\leq M _ G) の辺は頂点 u _ i と頂点 v _ i を結んでいます。 H には M _ H 本の辺があり、i 本目 (1\leq i\leq M _ H) の辺は頂点 a _ i と頂点 b _ i を結んでいます。
あなたは、グラフ H に対して次の操作を 0 回以上の好きな回数繰り返すことができます。
- 1\leq i\lt j\leq N を満たす整数の組 (i,j) をひとつ選ぶ。A _ {i,j} 円を支払って、頂点 i と頂点 j を結ぶ辺がなければ追加し、あれば取り除く。
G と H を同型にするために少なくとも何円支払う必要があるか求めてください。
単純無向グラフとは?
単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。
グラフの同型とは?
N 頂点のグラフ G と H が同型であるとは、ある (1,2,\ldots,N) の並べ替え (P _ 1,P _ 2,\ldots,P _ N) が存在して、どの 1\leq i\lt j\leq N に対しても
- G に頂点 i, 頂点 j を結ぶ辺が存在するとき、かつそのときに限り H に頂点 P _ i, 頂点 P _ j を結ぶ辺が存在する
制約
- 1\leq N\leq8
- 0\leq M _ G\leq\dfrac{N(N-1)}2
- 0\leq M _ H\leq\dfrac{N(N-1)}2
- 1\leq u _ i\lt v _ i\leq N\ (1\leq i\leq M _ G)
- (u _ i,v _ i)\neq(u _ j,v _ j)\ (1\leq i\lt j\leq M _ G)
- 1\leq a _ i\lt b _ i\leq N\ (1\leq i\leq M _ H)
- (a _ i,b _ i)\neq(a _ j,b _ j)\ (1\leq i\lt j\leq M _ H)
- 1\leq A _ {i,j}\leq 10 ^ 6\ (1\leq i\lt j\leq N)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N
M _ G
u _ 1 v _ 1
u _ 2 v _ 2
\vdots
u _ {M _ G} v _ {M _ G}
M _ H
a _ 1 b _ 1
a _ 2 b _ 2
\vdots
a _ {M _ H} b _ {M _ H}
A _ {1,2} A _ {1,3} \ldots A _ {1,N}
A _ {2,3} \ldots A _ {2,N}
\vdots
A _ {N-1,N}
出力
答えを出力せよ。
入力例 1
5 4 1 2 2 3 3 4 4 5 4 1 2 1 3 1 4 1 5 3 1 4 1 5 9 2 6 5 3
出力例 1
9
与えられたグラフはそれぞれ以下のようになります。

たとえば、H に対して次のような 4 つの操作を順に行うことで、9 円を支払ってG と H を同型にすることができます。
- (i,j)=(1,3) として操作を行う。H には頂点 1 と頂点 3 を結ぶ辺があるので、1 円を支払ってこれを取り除く。
- (i,j)=(2,5) として操作を行う。H には頂点 2 と頂点 5 を結ぶ辺はないので、2 円を支払ってこれを追加する。
- (i,j)=(1,5) として操作を行う。H には頂点 1 と頂点 5 を結ぶ辺があるので、1 円を支払ってこれを取り除く。
- (i,j)=(3,5) として操作を行う。H には頂点 3 と頂点 5 を結ぶ辺はないので、5 円を支払ってこれを追加する。
操作の結果、H は以下のようになります。

支払う金額を 8 円以下にして G と H を同型にすることはできないため、9 を出力してください。
入力例 2
5 3 1 2 2 3 3 4 4 1 2 2 3 3 4 4 5 9 1 1 1 1 1 1 1 1 9
出力例 2
3
たとえば、(i,j)=(2,3),(2,4),(3,4) とした 3 回の操作を行うことで G と H を同型にすることができます。
入力例 3
5 3 1 2 2 3 3 4 4 1 2 2 3 3 4 4 5 5 4 4 4 4 4 4 4 4 5
出力例 3
5
たとえば、(i,j)=(4,5) とした 1 回の操作を行うことで G と H を同型にすることができます。
入力例 4
2 0 0 371
出力例 4
0
G や H には辺が含まれていないこともあります。 また、一度も操作をする必要がないこともあります。
入力例 5
8 13 1 8 5 7 4 6 1 5 7 8 1 6 1 2 5 8 2 6 5 6 6 7 3 7 4 8 15 3 5 1 7 4 6 3 8 7 8 1 2 5 6 1 6 1 5 1 4 2 8 2 6 2 4 4 7 1 3 7483 1694 5868 3296 9723 5299 4326 5195 4088 5871 1384 2491 6562 1149 6326 2996 9845 7557 4041 7720 1554 5060 8329 8541 3530 4652 3874 3748
出力例 5
21214
Score : 300 points
Problem Statement
You are given simple undirected graphs G and H, each with N vertices: vertices 1, 2, \ldots, N. Graph G has M_G edges, and its i-th edge (1\leq i\leq M_G) connects vertices u_i and v_i. Graph H has M_H edges, and its i-th edge (1\leq i\leq M_H) connects vertices a_i and b_i.
You can perform the following operation on graph H any number of times, possibly zero.
- Choose a pair of integers (i,j) satisfying 1\leq i<j\leq N. Pay A_{i,j} yen, and if there is no edge between vertices i and j in H, add one; if there is, remove it.
Find the minimum total cost required to make G and H isomorphic.
What is a simple undirected graph?
A simple undirected graph is a graph without self-loops or multi-edges, where edges have no direction.
What does it mean for graphs to be isomorphic?
Two graphs G and H with N vertices are isomorphic if and only if there exists a permutation (P_1,P_2,\ldots,P_N) of (1,2,\ldots,N) such that for all 1\leq i\lt j\leq N:
- an edge exists between vertices i and j in G if and only if an edge exists between vertices P_i and P_j in H.
Constraints
- 1\leq N\leq8
- 0\leq M _ G\leq\dfrac{N(N-1)}2
- 0\leq M _ H\leq\dfrac{N(N-1)}2
- 1\leq u _ i\lt v _ i\leq N\ (1\leq i\leq M _ G)
- (u _ i,v _ i)\neq(u _ j,v _ j)\ (1\leq i\lt j\leq M _ G)
- 1\leq a _ i\lt b _ i\leq N\ (1\leq i\leq M _ H)
- (a _ i,b _ i)\neq(a _ j,b _ j)\ (1\leq i\lt j\leq M _ H)
- 1\leq A _ {i,j}\leq 10 ^ 6\ (1\leq i\lt j\leq N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
M _ G
u _ 1 v _ 1
u _ 2 v _ 2
\vdots
u _ {M _ G} v _ {M _ G}
M _ H
a _ 1 b _ 1
a _ 2 b _ 2
\vdots
a _ {M _ H} b _ {M _ H}
A _ {1,2} A _ {1,3} \ldots A _ {1,N}
A _ {2,3} \ldots A _ {2,N}
\vdots
A _ {N-1,N}
Output
Print the answer.
Sample Input 1
5 4 1 2 2 3 3 4 4 5 4 1 2 1 3 1 4 1 5 3 1 4 1 5 9 2 6 5 3
Sample Output 1
9
The given graphs are as follows:

For example, you can perform the following four operations on H to make it isomorphic to G at a cost of 9 yen.
- Choose (i,j)=(1,3). There is an edge between vertices 1 and 3 in H, so pay 1 yen to remove it.
- Choose (i,j)=(2,5). There is no edge between vertices 2 and 5 in H, so pay 2 yen to add it.
- Choose (i,j)=(1,5). There is an edge between vertices 1 and 5 in H, so pay 1 yen to remove it.
- Choose (i,j)=(3,5). There is no edge between vertices 3 and 5 in H, so pay 5 yen to add it.
After these operations, H becomes:

You cannot make G and H isomorphic at a cost less than 9 yen, so print 9.
Sample Input 2
5 3 1 2 2 3 3 4 4 1 2 2 3 3 4 4 5 9 1 1 1 1 1 1 1 1 9
Sample Output 2
3
For example, performing the operations (i,j)=(2,3),(2,4),(3,4) on H will make it isomorphic to G.
Sample Input 3
5 3 1 2 2 3 3 4 4 1 2 2 3 3 4 4 5 5 4 4 4 4 4 4 4 4 5
Sample Output 3
5
For example, performing the operation (i,j)=(4,5) once will make G and H isomorphic.
Sample Input 4
2 0 0 371
Sample Output 4
0
Note that G and H may have no edges.
Also, it is possible that no operations are needed.
Sample Input 5
8 13 1 8 5 7 4 6 1 5 7 8 1 6 1 2 5 8 2 6 5 6 6 7 3 7 4 8 15 3 5 1 7 4 6 3 8 7 8 1 2 5 6 1 6 1 5 1 4 2 8 2 6 2 4 4 7 1 3 7483 1694 5868 3296 9723 5299 4326 5195 4088 5871 1384 2491 6562 1149 6326 2996 9845 7557 4041 7720 1554 5060 8329 8541 3530 4652 3874 3748
Sample Output 5
21214
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
無限に広い 2 次元グリッドがあり、このグリッドの座標 (0,0) に焚き火があります。
時刻 t=0 では、マス (0,0) にのみ煙が存在します。
N, W, S, E からなる長さ N の文字列 S が与えられ、時刻 t=1,2,\dots,N では次の現象が順番に発生します。
- 風が吹き、現時点で存在する全ての煙が以下の通りに移動する。
- S の t 文字目が
Nであるとき、マス (r,c) にある煙がマス (r-1,c) に移動する。 - S の t 文字目が
Wであるとき、マス (r,c) にある煙がマス (r,c-1) に移動する。 - S の t 文字目が
Sであるとき、マス (r,c) にある煙がマス (r+1,c) に移動する。 - S の t 文字目が
Eであるとき、マス (r,c) にある煙がマス (r,c+1) に移動する。
- S の t 文字目が
- マス (0,0) に煙が存在しない場合、新たな煙がマス (0,0) に生成される。
高橋君はマス (R,C) に立っています。
整数 1 \le t \le N について、時刻 t+0.5 においてマス (R,C) に煙が存在するか判定し、出力欄の形式に従って出力してください。
制約
- N は 1 以上 200000 以下の整数
- S は
N,W,S,Eからなる長さ N の文字列 - R,C は -N 以上 N 以下の整数
- (R,C) \neq (0,0)
入力
入力は以下の形式で標準入力から与えられる。
N R C S
出力
答えを N 文字の 0, 1 からなる文字列として出力せよ。
出力する文字列のうち t 文字目 (1 \le t \le N) は次の通りにせよ。
- 時刻 t+0.5 においてマス (R,C) に煙が存在するなら
1 - 時刻 t+0.5 においてマス (R,C) に煙が存在しないなら
0
入力例 1
6 -2 1 NNEEWS
出力例 1
001010
時刻 1.5,2.5,4.5,6.5 ではマス (-2,1) には煙が存在せず、時刻 3.5,5.5 ではマス (-2,1) に煙が存在します。
よって、 001010 と出力します。
図では焚き火のあるマス (0,0) を基準として、マス (r,c) を
- r < 0 なら -r マス上に
- r \ge 0 なら r マス下に
- c < 0 なら -c マス左に
- c \ge 0 なら c マス右に
描画します。
時刻 0.5 でのグリッドの状態は次の通りです。
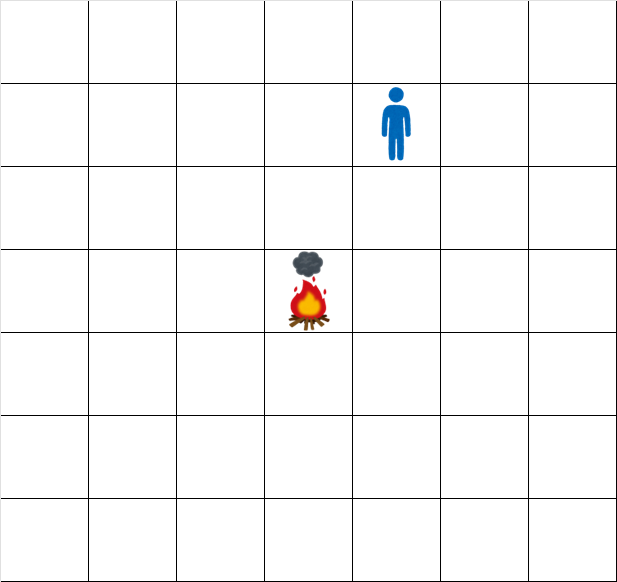
時刻 1.5 でのグリッドの状態は次の通りです。
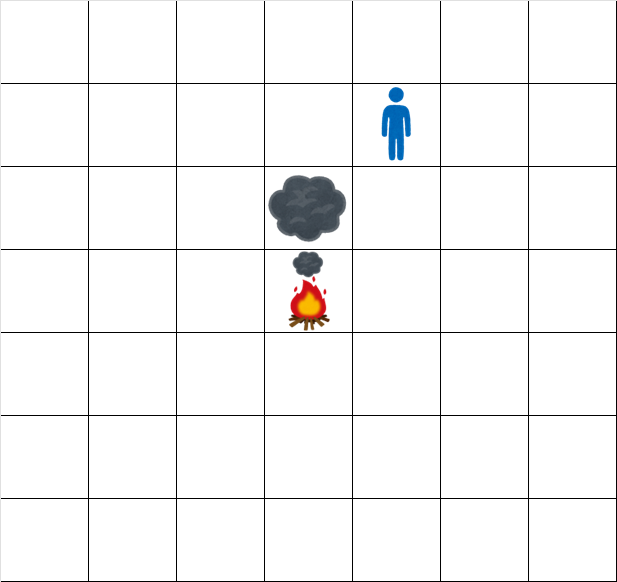
時刻 2.5 でのグリッドの状態は次の通りです。
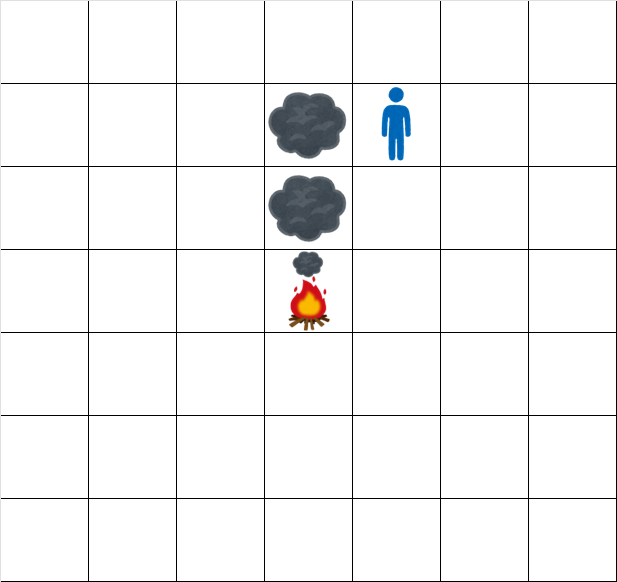
時刻 3.5 でのグリッドの状態は次の通りです。
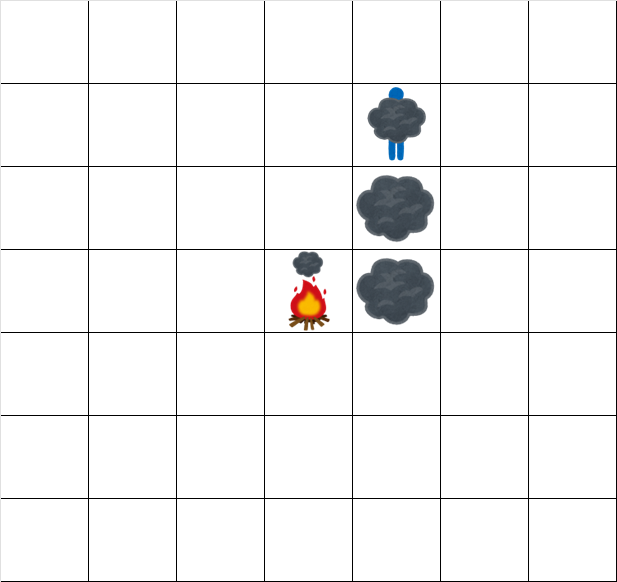
時刻 4.5 でのグリッドの状態は次の通りです。
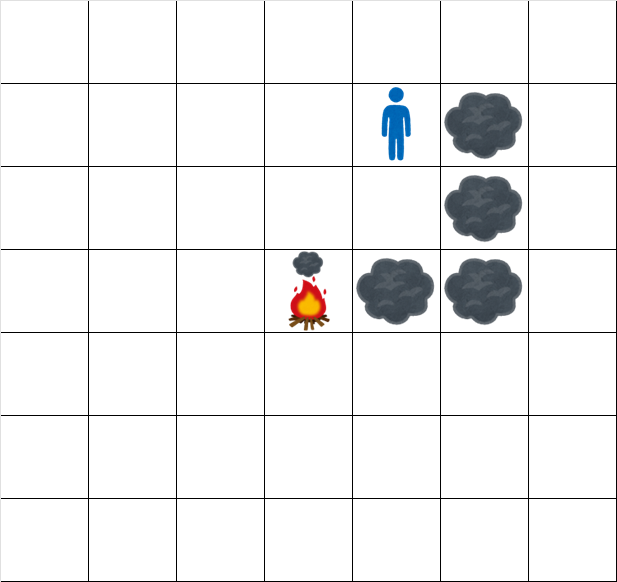
時刻 5.5 でのグリッドの状態は次の通りです。
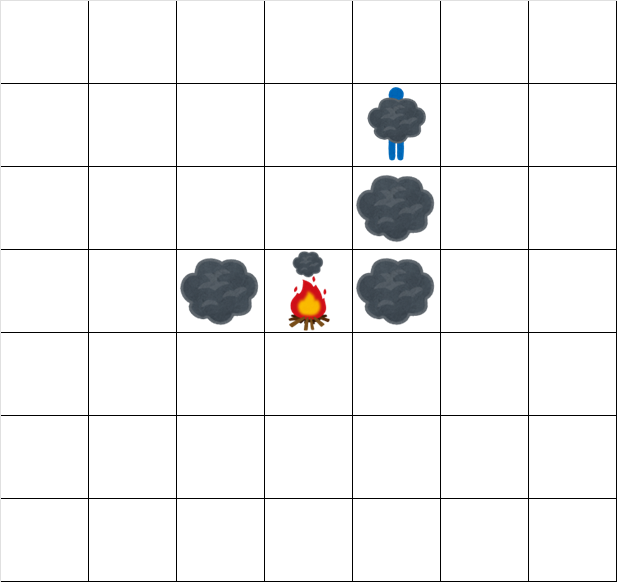
時刻 6.5 でのグリッドの状態は次の通りです。
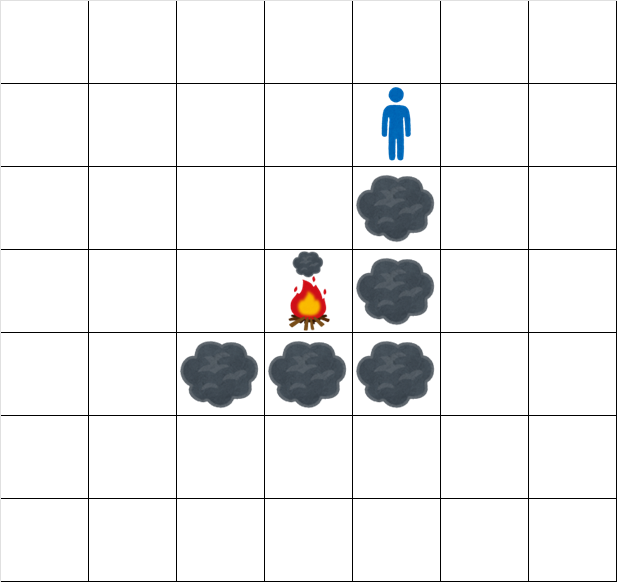
入力例 2
10 1 2 NEESESWEES
出力例 2
0001101011
入力例 3
20 -1 -2 WWNNWSWEWNSWWENSNWWN
出力例 3
00100111111000101111
Score : 425 points
Problem Statement
There is an infinitely large two-dimensional grid, with a campfire at coordinate (0,0).
At time t=0, smoke exists only at cell (0,0).
You are given a length-N string S consisting of N, W, S, E. At times t=1,2,\dots,N, the following happen in order:
- Wind blows, and all the smoke present at that time moves as follows:
- If the t-th character of S is
N, smoke in cell (r,c) moves to cell (r-1,c). - If it is
W, smoke in cell (r,c) moves to cell (r,c-1). - If it is
S, smoke in cell (r,c) moves to cell (r+1,c). - If it is
E, smoke in cell (r,c) moves to cell (r,c+1).
- If the t-th character of S is
- If there is no smoke in cell (0,0), new smoke is generated at cell (0,0).
Takahashi is standing at cell (R,C).
For each integer 1 \le t \le N, determine if smoke exists at cell (R,C) at time t+0.5, and print the response according to the required format.
Constraints
- N is an integer between 1 and 200000, inclusive.
- S is a length N string consisting of
N,W,S,E. - R and C are integers between -N and N, inclusive.
- (R,C) \neq (0,0)
Input
The input is given from Standard Input in the following format:
N R C S
Output
Print an N-character string consisting of 0 and 1.
The t-th character (1 \le t \le N) should be:
1if smoke exists at cell (R,C) at time t+0.5, and0otherwise.
Sample Input 1
6 -2 1 NNEEWS
Sample Output 1
001010
At times 1.5,2.5,4.5,6.5, there is no smoke at cell (-2,1). At times 3.5,5.5, there is smoke at cell (-2,1).
Hence, output 001010.
In the figures below, taking cell (0,0) with the campfire as a reference, cell (r,c) is drawn:
- -r cells up if r < 0,
- r cells down if r \ge 0,
- -c cells left if c < 0,
- c cells right if c \ge 0.
The grid at time 0.5 looks like:

The grid at time 1.5 looks like:

The grid at time 2.5 looks like:

The grid at time 3.5 looks like:

The grid at time 4.5 looks like:

The grid at time 5.5 looks like:

The grid at time 6.5 looks like:

Sample Input 2
10 1 2 NEESESWEES
Sample Output 2
0001101011
Sample Input 3
20 -1 -2 WWNNWSWEWNSWWENSNWWN
Sample Output 3
00100111111000101111