AtCoder Daily Training MEDIUM 2025/08/19 15:30start

C - Not All

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 200 点

問題文

長さ N の整数列 A=(A_1,A_2,\dots,A_N) および正整数 M が与えられます。

A の末尾の要素を削除するという操作を 0 回以上 N 回以下行うことで、以下の条件が満たされないようにしたいです。

条件：A には 1 以上 M 以下の整数がすべて含まれている。

必要な操作回数の最小値を求めてください。

なお、本問題の制約下において、操作を 0 回以上 N 回以下行うことで上述の条件が満たされないようにすることが必ず可能であることが証明できます。

制約

1\leq M \leq N \leq 100
1\leq A_i \leq M
入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 A_2 \dots A_N

出力

条件が満たされなくなるために必要な操作回数の最小値を出力せよ。

入力例 1

5 3
3 2 3 1 2

出力例 1

最初、A=(3,2,3,1,2) です。このとき、A には 1 以上 3 以下の整数がすべて含まれるため条件を満たします。

A の末尾の要素を削除する操作を 1 回行うと、A=(3,2,3,1) となります。このとき、A には 1 以上 3 以下の整数がすべて含まれるため条件を満たします。

A の末尾の要素を削除する操作をもう 1 回行うと、A=(3,2,3) となります。このとき、A には 1 が含まれないため条件を満たしません。

よって、条件が満たされなくなるために必要な操作回数の最小値は 2 です。

入力例 2

4 3
1 3 1 3

出力例 2

A には最初から 2 が含まれず条件を満たさないため、操作を 1 回も行う必要がありません。

入力例 3

10 4
1 3 3 4 2 1 3 1 2 4

出力例 3

Score : 200 points

Problem Statement

You are given an integer sequence A = (A_1, A_2, \dots, A_N) of length N and a positive integer M.

Your goal is to make the following condition false by performing this operation between 0 and N times (inclusive): remove the last element of A.

Condition: A contains every integer from 1 through M.

Find the minimum number of operations required.

Under the constraints of this problem, it can be proved that it is always possible to make the condition false by performing the operation between 0 and N times.

Constraints

1 \le M \le N \le 100
1 \le A_i \le M
All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 A_2 \dots A_N

Output

Output the minimum number of operations required to make the condition false.

Sample Input 1

5 3
3 2 3 1 2

Sample Output 1

Initially, A = (3,2,3,1,2). Since A contains every integer from 1 through 3, the condition holds.

If you perform the operation once, A = (3,2,3,1). The condition still holds.

If you perform the operation once more, A = (3,2,3). The integer 1 is missing, so the condition no longer holds.

Therefore, the minimum required number of operations is 2.

Sample Input 2

4 3
1 3 1 3

Sample Output 2

Since A initially lacks the integer 2, the condition is already false, so no operation is needed.

Sample Input 3

10 4
1 3 3 4 2 1 3 1 2 4

Sample Output 3

D - Distance Table

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 200 点

問題文

N 個の駅、駅 1, 駅 2, \ldots, 駅 N が直線上にこの順に並んでいます。
ここで、1\leq i\leq N-1 について、駅 i と駅 (i+1) の間の距離は D_i です。

1\leq i<j\leq N をみたす整数の組 (i,j) それぞれについて、駅 i と駅 j の間の距離を求めてください。
なお、出力形式については出力の欄を参照してください。

制約

2 \leq N \leq 50
1 \leq D_i \leq 100
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられる。

N
D_1 D_2 \ldots D_{N-1}

出力

N-1 行出力せよ。
i 行目 (1\leq i\leq N-1) には、(N-i) 個の整数を空白区切りで出力せよ。
i 行目の j 番目 (1\leq j\leq N-i) には、駅 i と駅 (i+j) の間の距離を出力せよ。

入力例 1

5
5 10 2 3

出力例 1

各駅の間の距離は次のようになります。

駅 1 と駅 2 の間の距離は 5 です。
駅 1 と駅 3 の間の距離は 5+10=15 です。
駅 1 と駅 4 の間の距離は 5+10+2=17 です。
駅 1 と駅 5 の間の距離は 5+10+2+3=20 です。
駅 2 と駅 3 の間の距離は 10 です。
駅 2 と駅 4 の間の距離は 10+2=12 です。
駅 2 と駅 5 の間の距離は 10+2+3=15 です。
駅 3 と駅 4 の間の距離は 2 です。
駅 3 と駅 5 の間の距離は 2+3=5 です。
駅 4 と駅 5 の間の距離は 3 です。

よって、上記のように出力します。

入力例 2

2
100

出力例 2

Score : 200 points

Problem Statement

There are N stations, station 1, station 2, \ldots, station N, arranged in this order on a straight line.
Here, for 1\leq i\leq N-1, the distance between stations i and (i+1) is D_i.

For each pair of integers (i,j) satisfying 1\leq i<j\leq N, find the distance between stations i and j.
For the output format, refer to the Output section.

Constraints

2 \leq N \leq 50
1 \leq D_i \leq 100
All input values are integers.

Input

The input is given from Standard Input in the following format:

N
D_1 D_2 \ldots D_{N-1}

Output

Output N-1 lines.
On the i-th line (1\leq i\leq N-1), output (N-i) integers, separated by spaces.
The j-th integer on the i-th line (1\leq j\leq N-i) should be the distance between stations i and (i+j).

Sample Input 1

5
5 10 2 3

Sample Output 1

The distances between stations are as follows:

The distance between stations 1 and 2 is 5.
The distance between stations 1 and 3 is 5+10=15.
The distance between stations 1 and 4 is 5+10+2=17.
The distance between stations 1 and 5 is 5+10+2+3=20.
The distance between stations 2 and 3 is 10.
The distance between stations 2 and 4 is 10+2=12.
The distance between stations 2 and 5 is 10+2+3=15.
The distance between stations 3 and 4 is 2.
The distance between stations 3 and 5 is 2+3=5.
The distance between stations 4 and 5 is 3.

Thus, output as shown above.

Sample Input 2

2
100

Sample Output 2

E - Cycle Graph?

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 300 点

問題文

N 頂点 M 辺の単純無向グラフが与えられます。頂点には 1,2,\dots,N の番号が、辺には 1,2,\dots,M の番号がつけられており、辺 i は頂点 A_i と頂点 B_i を結んでいます。

このグラフがサイクルグラフであるか判定してください。

単純無向グラフとは

単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。

サイクルグラフとは

頂点に 1, 2, \dots, N の番号が付けられた N 頂点のグラフがサイクルグラフであるとは、(1, 2, \dots, N) を並べ変えて得られる数列 (v_1, v_2, \dots, v_N) であって、以下の条件を満たすものが存在することをいいます。

i = 1, 2, \dots, N-1 に対して、頂点 v_i と v_{i+1} を結ぶ辺が存在する
頂点 v_N と v_1 を結ぶ辺が存在する
それら以外の辺は存在しない

制約

3\leq N \leq 2\times 10^5
0 \leq M \leq 2\times 10^5
1 \leq A_i, B_i \leq N
与えられるグラフは単純
入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 B_1
\vdots
A_M B_M

出力

与えられたグラフがサイクルグラフであるなら Yes、そうでないなら No と出力せよ。

入力例 1

出力例 1

Yes

与えられたグラフは以下の通りであり、これはサイクルグラフです。

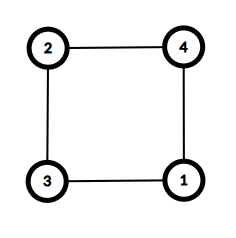
入力例 2

出力例 2

No

与えられたグラフは以下の通りであり、これはサイクルグラフではありません。

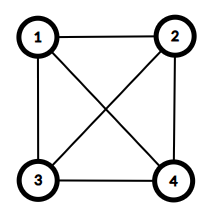
Score : 300 points

Problem Statement

You are given a simple undirected graph with N vertices and M edges. The vertices are numbered 1,2,\dots,N and the edges are numbered 1,2,\dots,M. Edge i connects vertices A_i and B_i.

Determine whether this graph is a cycle graph.

Definition of simple undirected graph

A simple undirected graph is a graph with undirected edges without self-loops or multi-edges.

Definition of cycle graph

An N-vertex graph with vertices labeled 1,2,\dots,N is a cycle graph when there exists a permutation (v_1,v_2,\dots,v_N) of (1,2,\dots,N) such that:

For each i = 1,2,\dots,N-1, there is an edge between vertices v_i and v_{i+1}.
There is an edge between vertices v_N and v_1.
No other edges exist.

Constraints

3 \le N \le 2\times 10^5
0 \le M \le 2\times 10^5
1 \le A_i, B_i \le N
The given graph is simple.
All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 B_1
\vdots
A_M B_M

Output

Output Yes if the given graph is a cycle graph; otherwise, print No.

Sample Input 1

Sample Output 1

Yes

The given graph is as follows, and this is a cycle graph.

Sample Input 2

Sample Output 2

No

The given graph is as follows, and this is not a cycle graph.

F - Palindromic in Both Bases

Time Limit: 3 sec / Memory Limit: 1024 MiB

配点 : 350 点

問題文

414 の十進法での表記は 414 であり、これは回文です。また、414 の八進法での表記は 636 であり、これも回文です。これを踏まえて、以下の問題を解いてください。

正の整数 A, N が与えられます。 1 以上 N 以下の整数のうち、十進法での表記も A 進法での表記も回文であるようなものの総和を求めてください。

なお、この問題の制約下で答えは 2^{63} 未満であることが証明できます。

制約

2 \leq A \leq 9
1 \leq N \le 10^{12}
入力される数値は全て整数である。

入力

入力は以下の形式で標準入力から与えられる。

A
N

出力

答えを 1 行で出力せよ。

入力例 1

8
1000

出力例 1

条件を満たす整数は 1,2,3,4,5,6,7,9,121,292,333,373,414,585 の 14 個であり、その総和は 2155 です。

入力例 2

8
999999999999

出力例 2

914703021014

入力例 3

6
999999999999

出力例 3

283958331810

Score : 350 points

Problem Statement

The decimal representation of 414 is 414, which is a palindrome. Also, the octal representation of 414 is 636, which is also a palindrome. Based on this, solve the following problem.

You are given positive integers A and N. Find the sum of all integers between 1 and N, inclusive, whose decimal representation and base-A representation are both palindromes.

Under the constraints of this problem, it can be proved that the answer is less than 2^{63}.

Constraints

2 \leq A \leq 9
1 \leq N \le 10^{12}
All input values are integers.

Input

The input is given from Standard Input in the following format:

A
N

Output

Output the answer in one line.

Sample Input 1

8
1000

Sample Output 1

The integers satisfying the condition are 1,2,3,4,5,6,7,9,121,292,333,373,414,585 (14 integers), and their sum is 2155.

Sample Input 2

8
999999999999

Sample Output 2

914703021014

Sample Input 3

6
999999999999

Sample Output 3

283958331810

G - String Rotation

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 400 点

問題文

長さ N の英小文字からなる文字列 S=S_1S_2\dots S_N が与えられます。あなたは、S に対して以下の操作をちょうど 1 回行います。

S の長さ 1 以上の連続部分文字列を選んで、左に 1 だけ巡回シフトする。すなわち、整数 1 \leq \ell \leq r \leq N を選んで、S の r 文字目の右に S_\ell を挿入したのち、S の \ell 番目の文字を削除する。

操作後の S としてありえる文字列のうち、辞書順最小のものを求めてください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

1 \leq T \leq 10^5
1 \leq N \leq 10^5
S は英小文字からなる長さ N の文字列
T,N は整数
1 つの入力ファイルに含まれる N の総和は 10^5 以下

入力

入力は以下の形式で標準入力から与えられる。

T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T

各テストケース \mathrm{case}_i\;(1 \leq i \leq T) は以下の形式で与えられる。

N
S

出力

T 行出力せよ。i \; (1 \leq i \leq T) 行目には、\mathrm{case}_i に対する答えを出力せよ。

入力例 1

3
7
atcoder
1
x
5
snuke

出力例 1

acodert
x
nsuke

1 番目のテストケースでは、2 文字目から 7 文字目を巡回シフトして acodert とするのが辞書順最小です。
2 番目のテストケースでは、どのように操作しても x が得られます。
3 番目のテストケースでは、1 文字目から 2 文字目を巡回シフトして nsuke とするのが辞書順最小です。

Score : 400 points

Problem Statement

You are given a string S=S_1S_2\dots S_N of length N consisting of lowercase English letters. You will perform the following operation on S exactly once:

Choose a contiguous substring of S with length at least 1 and cyclically shift it to the left by 1. That is, choose integers 1 \leq \ell \leq r \leq N, insert S_\ell to the right of the r-th character of S, and then delete the \ell-th character of S.

Find the lexicographically smallest string among all possible strings that S can become after the operation.

You are given T test cases, so solve each of them.

Constraints

1 \leq T \leq 10^5
1 \leq N \leq 10^5
S is a string of length N consisting of lowercase English letters.
T and N are integers.
The sum of N over all test cases in a single input file is at most 10^5.

Input

The input is given from Standard Input in the following format:

T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T

Each test case \mathrm{case}_i\;(1 \leq i \leq T) is given in the following format:

N
S

Output

Output T lines. The i-th (1 \leq i \leq T) line should contain the answer for \mathrm{case}_i.

Sample Input 1

3
7
atcoder
1
x
5
snuke

Sample Output 1

acodert
x
nsuke

In the first test case, cyclically shifting from the 2nd to the 7th character gives acodert, which is lexicographically smallest.
In the second test case, no matter how you operate, you get x.
In the third test case, cyclically shifting from the 1st to the 2nd character gives nsuke, which is lexicographically smallest.