Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
次の図に示す、各マスが黒または白に塗られた縦 15 行 \times 横 15 列のグリッドにおいて、 上から R 行目、左から C 列目のマスが何色かを出力して下さい。

制約
- 1 \leq R, C \leq 15
- R, C は整数
入力
入力は以下の形式で標準入力から与えられる。
R C
出力
図のグリッドにおいて上から R 行目、左から C 列目のマスが黒色の場合は black と、白色の場合は white と出力せよ。
ジャッジは英小文字と英大文字を厳密に区別することに注意せよ。
入力例 1
3 5
出力例 1
black
図のグリッドにおいて上から 3 行目、左から 5 列目のマスは黒色です。
よって、black と出力します。
入力例 2
4 5
出力例 2
white
図のグリッドにおいて上から 4 行目、左から 5 列目のマスは白色です。
よって、white と出力します。
Score : 200 points
Problem Statement
Print the color of the cell at the R-th row from the top and C-th column from the left in the following grid with 15 vertical rows and 15 horizontal columns.

Constraints
- 1 \leq R, C \leq 15
- R and C are integers.
Input
Input is given from Standard Input in the following format:
R C
Output
In the grid above, if the color of the cell at the R-th row from the top and C-th column from the left is black, then print black; if the cell is white, then print white. Note that the judge is case-sensitive.
Sample Input 1
3 5
Sample Output 1
black
In the grid above, the cell at the 3-rd row from the top and 5-th column from the left is black. Thus, black should be printed.
Sample Input 2
4 5
Sample Output 2
white
In the grid above, the cell at the 4-th row from the top and 5-th column from the left is white. Thus, white should be printed.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
N 個の台が一列に並んでおり、左から i 番目の台の高さは H_i です。
高橋君は最初、左端の台の上に立っています。
高橋君は高い所が好きなので、次のルールで可能な限り移動を繰り返します。
- いま立っているのが右端の台ではなく、かつ、右隣にある台の高さが自分がいま立っている台より高いとき、右隣の台に移動する
最終的に高橋君が立っている台の高さを求めてください。
制約
- 2 \leq N \leq 10^5
- 1 \leq H_i \leq 10^9
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N H_1 \ldots H_N
出力
答えを出力せよ。
入力例 1
5 1 5 10 4 2
出力例 1
10
最初、高橋君は左端にある高さ 1 の台に立っています。右隣の台の高さは 5 であり、いま立っている台より高いので、右隣の台に移動します。
移動後、高橋君は左から 2 番目にある高さ 5 の台に立っています。右隣の台の高さは 10 であり、いま立っている台より高いので、右隣の台に移動します。
移動後、高橋君は左から 3 番目にある高さ 10 の台に立っています。右隣の台の高さは 4 であり、いま立っている台より低いので、高橋君は移動をやめます。
よって、最終的に高橋君が立っている台の高さは 10 です。
入力例 2
3 100 1000 100000
出力例 2
100000
入力例 3
4 27 1828 1828 9242
出力例 3
1828
Score : 200 points
Problem Statement
There are N platforms arranged in a row. The height of the i-th platform from the left is H_i.
Takahashi is initially standing on the leftmost platform.
Since he likes heights, he will repeat the following move as long as possible.
- If the platform he is standing on is not the rightmost one, and the next platform to the right has a height greater than that of the current platform, step onto the next platform.
Find the height of the final platform he will stand on.
Constraints
- 2 \leq N \leq 10^5
- 1 \leq H_i \leq 10^9
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N H_1 \ldots H_N
Output
Print the answer.
Sample Input 1
5 1 5 10 4 2
Sample Output 1
10
Takahashi is initially standing on the leftmost platform, whose height is 1. The next platform to the right has a height of 5 and is higher than the current platform, so he steps onto it.
He is now standing on the 2-nd platform from the left, whose height is 5. The next platform to the right has a height of 10 and is higher than the current platform, so he steps onto it.
He is now standing on the 3-rd platform from the left, whose height is 10. The next platform to the right has a height of 4 and is lower than the current platform, so he stops moving.
Thus, the height of the final platform Takahashi will stand on is 10.
Sample Input 2
3 100 1000 100000
Sample Output 2
100000
Sample Input 3
4 27 1828 1828 9242
Sample Output 3
1828
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
正の整数 X は、次の条件をみたすときかつその時に限り、良い整数と呼ばれます。
- 正の整数の組 (a,b) を用いて、X=2^a\times b^2 と書ける。
例えば、400 は 400=2^2\times 10^2 と書けるため、良い整数です。
正の整数 N が与えられるので、1 以上 N 以下の良い整数の個数を求めてください。
制約
- 1 \leq N \leq 10^{18}
- N は整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
1 以上 N 以下の良い整数の個数を出力せよ。
入力例 1
20
出力例 1
5
1 以上 20 以下の良い整数は 2,4,8,16,18 の 5 つです。
よって、5 を出力します。
入力例 2
400
出力例 2
24
入力例 3
1234567890
出力例 3
42413
入力が 32bit 整数型に収まるとは限らないことに注意してください。
Score : 350 points
Problem Statement
A positive integer X is called a good integer if and only if it satisfies the following condition:
- There exists a pair of positive integers (a,b) such that X = 2^a \times b^2.
For example, 400 is a good integer because 400 = 2^2 \times 10^2.
Given a positive integer N, find the number of good integers between 1 and N, inclusive.
Constraints
- 1 \leq N \leq 10^{18}
- N is an integer.
Input
The input is given from Standard Input in the following format:
N
Output
Print the number of good integers between 1 and N, inclusive.
Sample Input 1
20
Sample Output 1
5
There are five good integers between 1 and 20: 2, 4, 8, 16, and 18.
Thus, print 5.
Sample Input 2
400
Sample Output 2
24
Sample Input 3
1234567890
Sample Output 3
42413
Note that the input might not fit in a 32-bit integer type.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
2 次元グリッド上に 2 つの図形 S と T があります。グリッドは正方形のマスからなります。
S は N 行 N 列のグリッド内にあり、S_{i,j} が # であるようなマス全体からなります。
T も N 行 N 列のグリッド内にあり、T_{i,j} が # であるようなマス全体からなります。
S と T を 90 度回転及び平行移動の繰り返しによって一致させることができるか判定してください。
制約
- 1 \leq N \leq 200
- S,T は
#と.のみからなる - S,T は 1 つ以上
#を含む
入力
入力は以下の形式で標準入力から与えられる。
N
S_{1,1}S_{1,2}\ldots S_{1,N}
\vdots
S_{N,1}S_{N,2}\ldots S_{N,N}
T_{1,1}T_{1,2}\ldots T_{1,N}
\vdots
T_{N,1}T_{N,2}\ldots T_{N,N}
出力
S と T を90 度回転及び平行移動の繰り返しによって一致させることができるとき Yes を、そうでないとき No を出力せよ。
入力例 1
5 ..... ..#.. .###. ..... ..... ..... ..... ....# ...## ....#
出力例 1
Yes
S を左回りに 90 度回転させ、平行移動することで T に一致させることができます。
入力例 2
5 ##### ##..# #..## ##### ..... ##### #..## ##..# ##### .....
出力例 2
No
90 度回転と平行移動の繰り返しによって一致させることはできません。
入力例 3
4 #... ..#. ..#. .... #... #... ..#. ....
出力例 3
Yes
S 及び T は連結とは限りません。
入力例 4
4 #... .##. ..#. .... ##.. #... ..#. ....
出力例 4
No
回転や移動の操作は連結成分ごとにできるわけではなく、S,T 全体に対して行うことに注意してください。
Score : 300 points
Problem Statement
We have two figures S and T on a two-dimensional grid with square cells.
S lies within a grid with N rows and N columns, and consists of the cells where S_{i,j} is #.
T lies within the same grid with N rows and N columns, and consists of the cells where T_{i,j} is #.
Determine whether it is possible to exactly match S and T by 90-degree rotations and translations.
Constraints
- 1 \leq N \leq 200
- Each of S and T consists of
#and.. - Each of S and T contains at least one
#.
Input
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}\ldots S_{1,N}
\vdots
S_{N,1}S_{N,2}\ldots S_{N,N}
T_{1,1}T_{1,2}\ldots T_{1,N}
\vdots
T_{N,1}T_{N,2}\ldots T_{N,N}
Output
Print Yes if it is possible to exactly match S and T by 90-degree rotations and translations, and No otherwise.
Sample Input 1
5 ..... ..#.. .###. ..... ..... ..... ..... ....# ...## ....#
Sample Output 1
Yes
We can match S to T by rotating it 90-degrees counter-clockwise and translating it.
Sample Input 2
5 ##### ##..# #..## ##### ..... ##### #..## ##..# ##### .....
Sample Output 2
No
It is impossible to match them by 90-degree rotations and translations.
Sample Input 3
4 #... ..#. ..#. .... #... #... ..#. ....
Sample Output 3
Yes
Each of S and T may not be connected.
Sample Input 4
4 #... .##. ..#. .... ##.. #... ..#. ....
Sample Output 4
No
Note that it is not allowed to rotate or translate just a part of a figure; it is only allowed to rotate or translate a whole figure.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
10^9 行 W 列のグリッドがあります。左から x 列目、下から y 行目のマスを (x,y) と表します。
N 個のブロックがあります。各ブロックは 1 \times 1 の正方形で、ブロック i (1 \leq i \leq N) は時刻 0 にマス (X_i,Y_i) にあります。
時刻 t=1,2,\dots,10^{100} に、以下のルールに従ってブロックを動かします。
- グリッドの下から 1 行目がすべてブロックで埋まっているならば、下から 1 行目にあるブロックをすべて消滅させる。
- 残っているブロックについて、下にあるブロックから順番に、以下の操作を行う。
- ブロックが一番下の行にある、またはそのブロックの 1 つ下のマスにもブロックがあるならば、何もしない
- そうでなければ、ブロックを 1 つ下のマスに動かす。
Q 個の質問が与えられます。j 番目 (1 \leq j \leq Q) の質問では、時刻 T_j+0.5 にブロック A_j が存在するかどうか答えてください。
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq W \leq N
- 1 \leq X_i \leq W
- 1 \leq Y_i \leq 10^9
- i \neq j なら (X_i,Y_i) \neq (X_j,Y_j)
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_j \leq 10^9
- 1 \leq A_j \leq N
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N Q T_1 A_1 T_2 A_2 \vdots T_Q A_Q
出力
Q 行出力せよ。i 行目には、時刻 T_i+0.5 にブロック A_i が存在するならば Yes を、存在しないならば No を出力せよ。
入力例 1
5 3 1 1 1 2 2 2 3 2 2 3 6 1 1 1 2 2 3 2 5 3 4 3 5
出力例 1
Yes Yes No Yes No Yes
ブロックの位置は以下のように変化します。
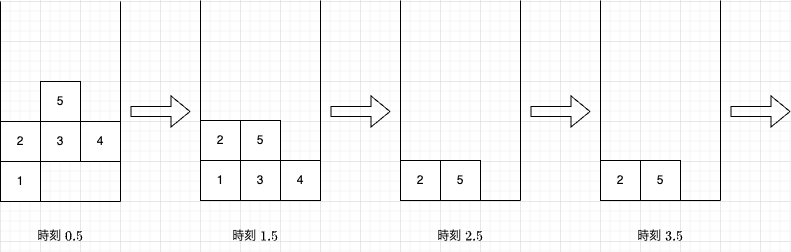
- 質問 1: 時刻 1.5 にブロック 1 は存在するので、答えは
Yesです。 - 質問 2: 時刻 1.5 にブロック 2 は存在するので、答えは
Yesです。 - 質問 3: ブロック 3 は時刻 2 に消滅します。よって、時刻 2.5 にブロック 3 は存在しないので、答えは
Noです。
入力例 2
3 2 1 1 2 1 1 2 4 1 1 1 2 1 3 2 3
出力例 2
No No Yes Yes
Score : 400 points
Problem Statement
There is a grid with 10^9 rows and W columns. The cell at the x-th column from the left and the y-th row from the bottom is denoted by (x,y).
There are N blocks. Each block is a 1 \times 1 square, and block i-th (1 \leq i \leq N) is located at cell (X_i,Y_i) at time 0.
At times t=1,2,\dots,10^{100}, the blocks are moved according to the following rules:
- If the entire bottom row is filled with blocks, then all blocks in the bottom row are removed.
- For each remaining block, in order from bottom to top, perform the following:
- If the block is in the bottom row, or if there is a block in the cell immediately below it, do nothing.
- Otherwise, move the block one cell downward.
You are given Q queries. For the j-th query (1 \leq j \leq Q), answer whether block A_j exists at time T_j+0.5.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq W \leq N
- 1 \leq X_i \leq W
- 1 \leq Y_i \leq 10^9
- (X_i,Y_i) \neq (X_j,Y_j) if i \neq j.
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_j \leq 10^9
- 1 \leq A_j \leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N Q T_1 A_1 T_2 A_2 \vdots T_Q A_Q
Output
Print Q lines. The i-th line should contain Yes if block A_i exists at time T_i+0.5, and No otherwise.
Sample Input 1
5 3 1 1 1 2 2 2 3 2 2 3 6 1 1 1 2 2 3 2 5 3 4 3 5
Sample Output 1
Yes Yes No Yes No Yes
The positions of the blocks change as follows: ("時刻" means "time.")

- Query 1: At time 1.5, block 1 exists, so the answer is
Yes. - Query 2: At time 1.5, block 2 exists, so the answer is
Yes. - Query 3: Block 3 disappears at time 2, so it does not exist at time 2.5, and the answer is
No.
Sample Input 2
3 2 1 1 2 1 1 2 4 1 1 1 2 1 3 2 3
Sample Output 2
No No Yes Yes