Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
高橋君は容量が G ml のグラスと、容量が M ml のマグカップを 1 つずつ持っています。
ここで、G,M は G<M をみたします。
最初、グラスとマグカップはいずれも空です。
以下の操作を K 回繰り返した後で、グラスとマグカップに水がそれぞれ何 ml ずつ入っているか求めてください。
- グラスが水で満たされているとき、すなわちグラスにちょうど G ml 入っているとき、グラスの水をすべて捨てる。
- そうでなく、マグカップが空であるとき、マグカップを水で満たす。
- 上のいずれでもないとき、マグカップが空になるかグラスが水で満たされるまで、マグカップからグラスに水を移す。
制約
- 1\leq K\leq 100
- 1\leq G<M\leq 1000
- G,M,K は整数
入力
入力は以下の形式で標準入力から与えられる。
K G M
出力
操作を K 回行った後で、グラスとマグカップに水がそれぞれ何 ml ずつ入っているか、この順に空白区切りで出力せよ。
入力例 1
5 300 500
出力例 1
200 500
操作は次の順で行われます。最初、グラスとマグカップはいずれも空です。
- マグカップを水で満たす。グラスには 0 ml, マグカップには 500 ml 入った状態になる。
- グラスが満たされるまでマグカップからグラスに水を移す。グラスには 300 ml, マグカップには 200 ml 入った状態になる。
- グラスの水をすべて捨てる。グラスには 0 ml, マグカップには 200 ml 入った状態になる。
- マグカップが空になるまでマグカップからグラスに水を移す。グラスには 200 ml, マグカップには 0 ml 入った状態になる。
- マグカップを水で満たす。グラスには 200 ml, マグカップには 500 ml 入った状態になる。
よって、5 回の操作の後でグラスには 200 ml, マグカップには 500 ml 入った状態になります。 ゆえに、200, 500 を空白区切りでこの順に出力します。
入力例 2
5 100 200
出力例 2
0 0
Score : 200 points
Problem Statement
AtCoder Inc. sells glasses and mugs.
Takahashi has a glass with a capacity of G milliliters and a mug with a capacity of M milliliters.
Here, G<M.
Initially, both the glass and the mug are empty.
After performing the following operation K times, determine how many milliliters of water are in the glass and the mug, respectively.
- When the glass is filled with water, that is, the glass contains exactly G milliliters of water, discard all the water from the glass.
- Otherwise, if the mug is empty, fill the mug with water.
- Otherwise, transfer water from the mug to the glass until the mug is empty or the glass is filled with water.
Constraints
- 1\leq K\leq 100
- 1\leq G<M\leq 1000
- G, M, and K are integers.
Input
The input is given from Standard Input in the following format:
K G M
Output
Print the amounts, in milliliters, of water in the glass and the mug, in this order, separated by a space, after performing the operation K times.
Sample Input 1
5 300 500
Sample Output 1
200 500
The operation will be performed as follows. Initially, both the glass and the mug are empty.
- Fill the mug with water. The glass has 0 milliliters, and the mug has 500 milliliters of water.
- Transfer water from the mug to the glass until the glass is filled. The glass has 300 milliliters, and the mug has 200 milliliters of water.
- Discard all the water from the glass. The glass has 0 milliliters, and the mug has 200 milliliters of water.
- Transfer water from the mug to the glass until the mug is empty. The glass has 200 milliliters, and the mug has 0 milliliters of water.
- Fill the mug with water. The glass has 200 milliliters, and the mug has 500 milliliters of water.
Thus, after five operations, the glass has 200 milliliters, and the mug has 500 milliliters of water. Hence, print 200 and 500 in this order, separated by a space.
Sample Input 2
5 100 200
Sample Output 2
0 0
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
1,\ldots,N の番号のついた N 人の選手がゲームを行いました。選手 i のスコアは A_i であり、スコアが小さい方が上位になります。
ブービー賞に該当する選手、すなわち、下位から 2 番目の選手の番号を求めてください。
制約
- 2 \leq N \leq 2\times 10^5
- 1 \leq A_i \leq 10^9
- A_i は相異なる
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N A_1 \ldots A_N
出力
答えを出力せよ。
入力例 1
6 1 123 12345 12 1234 123456
出力例 1
3
6 人中 5 位になるのは、選手 3 です。
入力例 2
5 3 1 4 15 9
出力例 2
5
Score : 200 points
Problem Statement
N players, who are numbered 1, \ldots, N, have played a game. Player i has scored A_i, and a player with a smaller score ranks higher.
The player who ranks the second lowest will receive a booby prize. Who is this player? Answer with an integer representing the player.
Constraints
- 2 \leq N \leq 2\times 10^5
- 1 \leq A_i \leq 10^9
- A_i are distinct.
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N A_1 \ldots A_N
Output
Print the answer.
Sample Input 1
6 1 123 12345 12 1234 123456
Sample Output 1
3
It is Player 3 who ranks fifth among the six players.
Sample Input 2
5 3 1 4 15 9
Sample Output 2
5
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
N 頂点 M 辺の単純無向グラフが与えられます。頂点には 1, 2, \dots, N の番号が、辺には 1, 2, \dots, M の番号が付けられています。
辺 i \, (i = 1, 2, \dots, M) は頂点 u_i, v_i を結んでいます。
このグラフがパスグラフであるか判定してください。
単純無向グラフとは
単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。
パスグラフとは
頂点に 1, 2, \dots, N の番号が付けられたN 頂点のグラフがパスグラフであるとは、(1, 2, \dots, N) を並べ変えて得られる数列 (v_1, v_2, \dots, v_N) であって、以下の条件を満たすものが存在することをいいます。
制約
- 2 \leq N \leq 2 \times 10^5
- 0 \leq M \leq 2 \times 10^5
- 1 \leq u_i, v_i \leq N \, (i = 1, 2, \dots, M)
- 入力される値は全て整数
- 入力で与えられるグラフは単純
入力
入力は以下の形式で標準入力から与えられる。
N M u_1 v_1 u_2 v_2 \vdots u_M v_M
出力
与えられたグラフがパスグラフなら Yes、そうでないなら No と出力せよ。
入力例 1
4 3 1 3 4 2 3 2
出力例 1
Yes
与えらえたグラフは下図のようであり、これはパスグラフです。

入力例 2
2 0
出力例 2
No
与えらえたグラフは下図のようであり、これはパスグラフではありません。

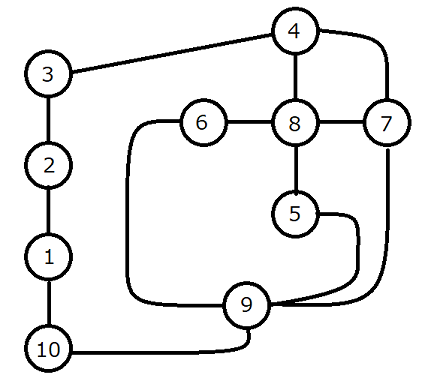
入力例 3
5 5 1 2 2 3 3 4 4 5 5 1
出力例 3
No
与えらえたグラフは下図のようであり、これはパスグラフではありません。

Score : 300 points
Problem Statement
You are given a simple undirected graph with N vertices and M edges. The vertices are numbered 1, 2, \dots, N, and the edges are numbered 1, 2, \dots, M.
Edge i \, (i = 1, 2, \dots, M) connects vertices u_i and v_i.
Determine if this graph is a path graph.
What is a simple undirected graph?
A simple undirected graph is a graph without self-loops or multiple edges whose edges do not have a direction.
What is a path graph?
A graph with N vertices numbered 1, 2, \dots, N is said to be a path graph if and only if there is a sequence (v_1, v_2, \dots, v_N) that is a permutation of (1, 2, \dots, N) and satisfies the following conditions:
Constraints
- 2 \leq N \leq 2 \times 10^5
- 0 \leq M \leq 2 \times 10^5
- 1 \leq u_i, v_i \leq N \, (i = 1, 2, \dots, M)
- All values in the input are integers.
- The graph given in the input is simple.
Input
The input is given from Standard Input in the following format:
N M u_1 v_1 u_2 v_2 \vdots u_M v_M
Output
Print Yes if the given graph is a path graph; print No otherwise.
Sample Input 1
4 3 1 3 4 2 3 2
Sample Output 1
Yes
Illustrated below is the given graph, which is a path graph.

Sample Input 2
2 0
Sample Output 2
No
Illustrated below is the given graph, which is not a path graph.

Sample Input 3
5 5 1 2 2 3 3 4 4 5 5 1
Sample Output 3
No
Illustrated below is the given graph, which is not a path graph.

Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
ある地方に、1 から N の番号がついた N 個の街と、1 から M の番号がついた M 本の道路があります。
i 番目の道路は街 A_i と街 B_i を双方向に結び、長さは C_i です。
好きな街からスタートして同じ街を二度以上通らずに別の街へ移動するときの、通る道路の長さの和としてありえる最大値を求めてください。
制約
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1\leq A_i < B_i \leq N
- (A_i,B_i) は相異なる
- 1\leq C_i \leq 10^8
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 C_1 \vdots A_M B_M C_M
出力
答えを出力せよ。
入力例 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
出力例 1
1110
4\to 1\to 3\to 2 と移動すると、通る道路の長さの和は 1110 となります。
入力例 2
10 1 5 9 1
出力例 2
1
道路と繋がっていない街が存在するかもしれません。
入力例 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
出力例 3
20
Score : 300 points
Problem Statement
A region has N towns numbered 1 to N, and M roads numbered 1 to M.
The i-th road connects town A_i and town B_i bidirectionally with length C_i.
Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.
Constraints
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1 \leq A_i < B_i \leq N
- The pairs (A_i,B_i) are distinct.
- 1\leq C_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 C_1 \vdots A_M B_M C_M
Output
Print the answer.
Sample Input 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
Sample Output 1
1110
If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.
Sample Input 2
10 1 5 9 1
Sample Output 2
1
There may be a town that is not connected to a road.
Sample Input 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
Sample Output 3
20

Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
N 以下の正整数のうち、 a<b<c なる 素数 a,b,c を用いて a^2 \times b \times c^2 と表せるものはいくつありますか?
制約
- N は 300 \le N \le 10^{12} を満たす整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを整数として出力せよ。
入力例 1
1000
出力例 1
3
1000 以下で条件を満たす整数は以下の 3 つです。
- 300 = 2^2 \times 3 \times 5^2
- 588 = 2^2 \times 3 \times 7^2
- 980 = 2^2 \times 5 \times 7^2
入力例 2
1000000000000
出力例 2
2817785
Score : 400 points
Problem Statement
How many positive integers no greater than N can be represented as a^2 \times b \times c^2 with three primes a,b, and c such that a<b<c?
Constraints
- N is an integer satisfying 300 \le N \le 10^{12}.
Input
The input is given from Standard Input in the following format:
N
Output
Print the answer as an integer.
Sample Input 1
1000
Sample Output 1
3
The conforming integers no greater than 1000 are the following three.
- 300 = 2^2 \times 3 \times 5^2
- 588 = 2^2 \times 3 \times 7^2
- 980 = 2^2 \times 5 \times 7^2
Sample Input 2
1000000000000
Sample Output 2
2817785