実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
縦 H 行横 W 列のマス目があります。上から i 行目、左から j 列目のマスをマス (i,j) と表します。
マス (i,j) は S_{i,j} が # のとき通行不可能、. のとき通行可能であり家が建っていない、@ のとき通行可能であり家が建っていることを表します。
最初、マス (X,Y) にサンタクロースがいます。サンタクロースは文字列 T に従って以下の行動を行います。
- 文字列 T の長さを |T| とする。i=1,2,\ldots,|T| の順に以下のように移動する。
- 現在サンタクロースがいるマスを (x,y) とする。
- T_i が
Uかつマス (x-1,y) が通行可能ならマス (x-1,y) に移動する。 - T_i が
Dかつマス (x+1,y) が通行可能ならマス (x+1,y) に移動する。 - T_i が
Lかつマス (x,y-1) が通行可能ならマス (x,y-1) に移動する。 - T_i が
Rかつマス (x,y+1) が通行可能ならマス (x,y+1) に移動する。 - それ以外の場合、マス (x,y) に留まる。
- T_i が
- 現在サンタクロースがいるマスを (x,y) とする。
行動を終えたあとにサンタクロースがいるマスと、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。
制約
- 3 \leq H,W \leq 100
- 1 \leq X \leq H
- 1 \leq Y \leq W
- 与えられる数値は全て整数である
- S_{i,j} は
#,.,@のいずれか - 全ての 1 \leq i \leq H について S_{i,1},S_{i,W} は
# - 全ての 1 \leq j \leq W について S_{1,j},S_{H,j} は
# - S_{X,Y}=
. - T は
U,D,L,Rのいずれかからなる長さ 1 以上 10^4 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
H W X Y
S_{1,1}S_{1,2}\ldots S_{1,W}
\dots
S_{H,1}S_{H,2}\ldots S_{H,W}
T
出力
行動を終えたあとサンタクロースがいるマスを (X,Y)、行動により通過または到達した家の数を C とするとき、X,Y,C をこの順に空白区切りで出力せよ。
入力例 1
5 5 3 4 ##### #...# #.@.# #..@# ##### LLLDRUU
出力例 1
2 3 1
サンタクロースは以下のように行動します。
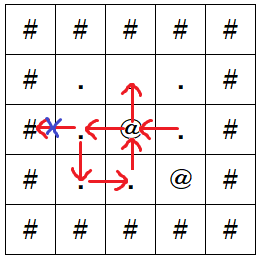
- T_1=
Lなのでマス (3,4) からマス (3,3) に移動する。これにより家を通過する。 - T_2=
Lなのでマス (3,3) からマス (3,2) に移動する。 - T_3=
Lだがマス (3,1) は通行不可能なので、マス (3,2) に留まる。 - T_4=
Dなのでマス (3,2) からマス (4,2) に移動する。 - T_5=
Rなのでマス (4,2) からマス (4,3) に移動する。 - T_6=
Uなのでマス (4,3) からマス (3,3) に移動する。これにより家を通過するが、この家はすでに通過したことがある家である。 - T_7=
Uなのでマス (3,3) からマス (2,3) に移動する。
行動により通過または到達した家の数は 1 です。
入力例 2
6 13 4 6 ############# #@@@@@@@@@@@# #@@@@@@@@@@@# #@@@@.@@@@@@# #@@@@@@@@@@@# ############# UURUURLRLUUDDURDURRR
出力例 2
3 11 11
入力例 3
12 35 7 10 ################################### #.................................# #..........@......................# #......@................@.........# #.............##............@.....# #...##........##....##............# #...##........##....##.......##...# #....##......##......##....##.....# #....##......##......##..##.......# #.....#######.........###.........# #.................................# ################################### LRURRRUUDDULUDUUDLRLRDRRLULRRUDLDRU
出力例 3
4 14 1
Score : 200 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
If S_{i,j} is #, the cell (i,j) is impassable; if it is ., the cell is passable and contains no house; if it is @, the cell is passable and contains a house.
Initially, Santa Claus is in cell (X,Y). He will act according to the string T as follows.
- Let |T| be the length of the string T. For i=1,2,\ldots,|T|, he moves as follows.
- Let (x,y) be the cell he is currently in.
- If T_i is
Uand cell (x-1,y) is passable, move to cell (x-1,y). - If T_i is
Dand cell (x+1,y) is passable, move to cell (x+1,y). - If T_i is
Land cell (x,y-1) is passable, move to cell (x,y-1). - If T_i is
Rand cell (x,y+1) is passable, move to cell (x,y+1). - Otherwise, stay in cell (x,y).
- If T_i is
- Let (x,y) be the cell he is currently in.
Find the cell where he is after completing all actions, and the number of distinct houses that he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.
Constraints
- 3 \leq H,W \leq 100
- 1 \leq X \leq H
- 1 \leq Y \leq W
- All given numbers are integers.
- Each S_{i,j} is one of
#,.,@. - S_{i,1} and S_{i,W} are
#for every 1 \leq i \leq H. - S_{1,j} and S_{H,j} are
#for every 1 \leq j \leq W. - S_{X,Y}=
. - T is a string of length at least 1 and at most 10^4, consisting of
U,D,L,R.
Input
The Input is given from Standard Input in the following format:
H W X Y
S_{1,1}S_{1,2}\ldots S_{1,W}
\dots
S_{H,1}S_{H,2}\ldots S_{H,W}
T
Output
Let (X,Y) be the cell where he is after completing all actions, and C be the number of distinct houses he passed through or arrived at during his actions. Print X,Y,C in this order separated by spaces.
Sample Input 1
5 5 3 4 ##### #...# #.@.# #..@# ##### LLLDRUU
Sample Output 1
2 3 1
Santa Claus behaves as follows:

- T_1=
L, so he moves from (3,4) to (3,3). A house is passed. - T_2=
L, so he moves from (3,3) to (3,2). - T_3=
L, but cell (3,1) is impassable, so he stays at (3,2). - T_4=
D, so he moves from (3,2) to (4,2). - T_5=
R, so he moves from (4,2) to (4,3). - T_6=
U, so he moves from (4,3) to (3,3). A house is passed, but it has already been passed. - T_7=
U, so he moves from (3,3) to (2,3).
The number of houses he passed or arrived during his actions is 1.
Sample Input 2
6 13 4 6 ############# #@@@@@@@@@@@# #@@@@@@@@@@@# #@@@@.@@@@@@# #@@@@@@@@@@@# ############# UURUURLRLUUDDURDURRR
Sample Output 2
3 11 11
Sample Input 3
12 35 7 10 ################################### #.................................# #..........@......................# #......@................@.........# #.............##............@.....# #...##........##....##............# #...##........##....##.......##...# #....##......##......##....##.....# #....##......##......##..##.......# #.....#######.........###.........# #.................................# ################################### LRURRRUUDDULUDUUDLRLRDRRLULRRUDLDRU
Sample Output 3
4 14 1
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
26 個のキーが数直線上に並んだキーボードがあります。
このキーボードの配列は ABCDEFGHIJKLMNOPQRSTUVWXYZ を並べ替えた文字列 S で表されます。
文字 S_x に対応するキーが座標 x (1 \leq x \leq 26) にあります。 ここで、S_x は S の x 文字目を表します。
あなたはこのキーボードを使って ABCDEFGHIJKLMNOPQRSTUVWXYZ をこの順で右手人差し指で一度だけ入力します。
ある文字を入力するためには、その文字に対応するキーの座標に指を移動させてキーを押す必要があります。
はじめ、指は A に対応するキーの座標にあります。A に対応するキーを押してから、Z に対応するキーを押すまでの指の移動距離の合計として考えられる最小値を求めてください。ただし、
キーを押す動作は移動距離に含まれません。
制約
- S は
ABCDEFGHIJKLMNOPQRSTUVWXYZを並べ替えた文字列である。
入力
入力は以下の形式で標準入力から与えられる。
S
出力
答えを出力せよ。
入力例 1
ABCDEFGHIJKLMNOPQRSTUVWXYZ
出力例 1
25
A のキーを押してから Z のキーを押すまで指を 1 ずつ正の方向に移動させる必要があり、このときの移動距離の合計は 25 です。25 未満の総移動距離でキーを全て入力することはできないため、25 と出力します。
入力例 2
MGJYIZDKSBHPVENFLQURTCWOAX
出力例 2
223
Score : 200 points
Problem Statement
There is a keyboard with 26 keys arranged on a number line.
The arrangement of this keyboard is represented by a string S, which is a permutation of ABCDEFGHIJKLMNOPQRSTUVWXYZ.
The key corresponding to the character S_x is located at coordinate x (1 \leq x \leq 26). Here, S_x denotes the x-th character of S.
You will use this keyboard to input ABCDEFGHIJKLMNOPQRSTUVWXYZ in this order, typing each letter exactly once with your right index finger.
To input a character, you need to move your finger to the coordinate of the key corresponding to that character and press the key.
Initially, your finger is at the coordinate of the key corresponding to A. Find the minimal possible total traveled distance of your finger from pressing the key for A to pressing the key for Z. Here, pressing a key does not contribute to the distance.
Constraints
- S is a permutation of
ABCDEFGHIJKLMNOPQRSTUVWXYZ.
Input
The input is given from Standard Input in the following format:
S
Output
Print the answer.
Sample Input 1
ABCDEFGHIJKLMNOPQRSTUVWXYZ
Sample Output 1
25
From pressing the key for A to pressing the key for Z, you need to move your finger 1 unit at a time in the positive direction, resulting in a total traveled distance of 25. It is impossible to press all keys with a total traveled distance less than 25, so print 25.
Sample Input 2
MGJYIZDKSBHPVENFLQURTCWOAX
Sample Output 2
223
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
長さ N の正整数列 A=(A_1,A_2,\dots,A_N) が与えられます。
1\leq l\leq r\leq N を満たす整数の組 (l,r) であって、数列 (A_l,A_{l+1},\dots,A_r) が等差数列であるようなものが何通りあるか求めてください。
なお、数列 (x_1,x_2,\dots,x_{|x|}) が等差数列であるとは、ある d が存在して x_{i+1}-x_i=d\ (1\leq i < |x|) であることをいいます。 特に、長さ 1 の数列は常に等差数列です。
制約
- 1\leq N \leq 2\times 10^5
- 1\leq A_i \leq 10^9
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \dots A_N
出力
答えを出力せよ。
入力例 1
4 3 6 9 3
出力例 1
8
条件を満たす整数の組 (l,r) は (1,1),(2,2),(3,3),(4,4),(1,2),(2,3),(3,4),(1,3) の 8 通りです。
実際、(l,r)=(1,3) のとき (A_l,\dots,A_r)=(3,6,9) は等差数列なので条件を満たしますが、 (l,r)=(2,4) のとき (A_l,\dots,A_r)=(6,9,3) は等差数列ではないので条件を満たしません。
入力例 2
5 1 1 1 1 1
出力例 2
15
すべての整数の組 (l,r)\ (1\leq l\leq r\leq 5) が条件を満たします。
入力例 3
8 87 42 64 86 72 58 44 30
出力例 3
22
Score : 300 points
Problem Statement
You are given a sequence of N positive integers A=(A_1,A_2,\dots,A_N).
Find the number of pairs of integers (l,r) satisfying 1\leq l\leq r\leq N such that the subsequence (A_l,A_{l+1},\dots,A_r) forms an arithmetic progression.
A sequence (x_1,x_2,\dots,x_{|x|}) is an arithmetic progression if and only if there exists a d such that x_{i+1}-x_i=d\ (1\leq i < |x|). In particular, a sequence of length 1 is always an arithmetic progression.
Constraints
- 1\leq N \leq 2\times 10^5
- 1\leq A_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \dots A_N
Output
Print the answer.
Sample Input 1
4 3 6 9 3
Sample Output 1
8
There are eight pairs of integers (l,r) satisfying the condition: (1,1),(2,2),(3,3),(4,4),(1,2),(2,3),(3,4),(1,3).
Indeed, when (l,r)=(1,3), (A_l,\dots,A_r)=(3,6,9) is an arithmetic progression, so it satisfies the condition. However, when (l,r)=(2,4), (A_l,\dots,A_r)=(6,9,3) is not an arithmetic progression, so it does not satisfy the condition.
Sample Input 2
5 1 1 1 1 1
Sample Output 2
15
All pairs of integers (l,r)\ (1\leq l\leq r\leq 5) satisfy the condition.
Sample Input 3
8 87 42 64 86 72 58 44 30
Sample Output 3
22
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
人 1, 人 2,\ldots, 人 N の N 人が一列に並んでいます。
並び方の情報が長さ N の数列 A=(A _ 1,A _ 2,\ldots,A _ N) として与えられます。
A _ i\ (1\leq i\leq N) は次のような情報を表しています。
- A _ i=-1 のとき、人 i は先頭に並んでいる。
- A _ i\neq -1 のとき、人 i は人 A _ i のすぐ後ろに並んでいる。
列に並んでいる人の番号を先頭から順番に出力してください。
制約
- 1\leq N\leq3\times10 ^ 5
- A _ i=-1 もしくは 1\leq A _ i\leq N\ (1\leq i\leq N)
- 情報と矛盾しないような N 人の並び方がただ 1 通り存在する
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A _ 1 A _ 2 \ldots A _ N
出力
人 s _ 1, 人 s _ 2,\ldots, 人 s _ N がこの順に列に並んでいるとき、s _ 1,s _ 2,\ldots,s _ N をこの順に空白を区切りとして出力せよ。
入力例 1
6 4 1 -1 5 3 2
出力例 1
3 5 4 1 2 6
先頭から、人 3, 人 5, 人 4, 人 1, 人 2, 人 6 がこの順に列に並んでいるとき、与えられた情報と一致しています。
実際、
- 人 1 は人 4 のすぐ後ろに並んでいます。
- 人 2 は人 1 のすぐ後ろに並んでいます。
- 人 3 は先頭に並んでいます。
- 人 4 は人 5 のすぐ後ろに並んでいます。
- 人 5 は人 3 のすぐ後ろに並んでいます。
- 人 6 は人 2 のすぐ後ろに並んでいます。
となり、与えられた情報と一致していることが確認できます。
よって、3,5,4,1,2,6 をこの順に空白区切りで出力してください。
入力例 2
10 -1 1 2 3 4 5 6 7 8 9
出力例 2
1 2 3 4 5 6 7 8 9 10
入力例 3
30 3 25 20 6 18 12 26 1 29 -1 21 17 23 9 8 30 10 15 22 27 4 13 5 11 16 24 28 2 19 7
出力例 3
10 17 12 6 4 21 11 24 26 7 30 16 25 2 28 27 20 3 1 8 15 18 5 23 13 22 19 29 9 14
Score: 300 points
Problem Statement
There are N people standing in a line: person 1, person 2, \ldots, person N.
You are given the arrangement of the people as a sequence A=(A _ 1,A _ 2,\ldots,A _ N) of length N.
A _ i\ (1\leq i\leq N) represents the following information:
- if A _ i=-1, person i is at the front of the line;
- if A _ i\neq -1, person i is right behind person A _ i.
Print the people's numbers in the line from front to back.
Constraints
- 1\leq N\leq3\times10 ^ 5
- A _ i=-1 or 1\leq A _ i\leq N\ (1\leq i\leq N)
- There is exactly one way to arrange the N people consistent with the information given.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A _ 1 A _ 2 \ldots A _ N
Output
If person s _ 1, person s _ 2, \ldots, person s _ N are standing in the line in this order, print s _ 1, s _ 2, \ldots, and s _ N in this order, separated by spaces.
Sample Input 1
6 4 1 -1 5 3 2
Sample Output 1
3 5 4 1 2 6
If person 3, person 5, person 4, person 1, person 2, and person 6 stand in line in this order from front to back, the arrangement matches the given information.
Indeed, it can be seen that:
- person 1 is standing right behind person 4,
- person 2 is standing right behind person 1,
- person 3 is at the front of the line,
- person 4 is standing right behind person 5,
- person 5 is standing right behind person 3, and
- person 6 is standing right behind person 2.
Thus, print 3, 5, 4, 1, 2, and 6 in this order, separated by spaces.
Sample Input 2
10 -1 1 2 3 4 5 6 7 8 9
Sample Output 2
1 2 3 4 5 6 7 8 9 10
Sample Input 3
30 3 25 20 6 18 12 26 1 29 -1 21 17 23 9 8 30 10 15 22 27 4 13 5 11 16 24 28 2 19 7
Sample Output 3
10 17 12 6 4 21 11 24 26 7 30 16 25 2 28 27 20 3 1 8 15 18 5 23 13 22 19 29 9 14
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
高橋君はすぬけ君たちを捕まえようとしています。
数直線上の座標 0,1,2,3,4 の 5 箇所に穴があり、すぬけ君たちの巣につながっています。
これから N 匹のすぬけ君が穴から出てきます。i 番目のすぬけ君は時刻 T_i に座標 X_i の穴から出てきて、大きさは A_i であることがわかっています。
高橋君は時刻 0 に座標 0 におり、数直線上を単位時間あたり 1 以下の速さで移動することができます。
すぬけ君が穴から出てきたのと同じ時刻に同じ座標に高橋君がいるとき、かつ、そのときに限り、高橋君はすぬけ君を捕まえることができます。
すぬけ君を捕まえるのにかかる時間は無視できます。
高橋君が適切に行動したとき、捕まえることができるすぬけ君の大きさの合計の最大値を求めてください。
制約
- 1 \leq N \leq 10^5
- 0 < T_1 < T_2 < \ldots < T_N \leq 10^5
- 0 \leq X_i \leq 4
- 1 \leq A_i \leq 10^9
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N T_1 X_1 A_1 T_2 X_2 A_2 \vdots T_N X_N A_N
出力
答えを整数として出力せよ。
入力例 1
3 1 0 100 3 3 10 5 4 1
出力例 1
101
次のように行動するのが最適です。
- 座標 0 で待機し、時刻 1 に 1 番目のすぬけ君を捕まえる
- 座標 4 へ移動し、時刻 5 に 3 番目のすぬけ君を捕まえる
1 番目と 2 番目のすぬけ君を両方とも捕まえることはできないので、これが最大です。
入力例 2
3 1 4 1 2 4 1 3 4 1
出力例 2
0
高橋君はすぬけ君を 1 匹も捕まえることができません。
入力例 3
10 1 4 602436426 2 1 623690081 3 3 262703497 4 4 628894325 5 3 450968417 6 1 161735902 7 1 707723857 8 2 802329211 9 0 317063340 10 2 125660016
出力例 3
2978279323
Score : 400 points
Problem Statement
Takahashi is trying to catch many Snuke.
There are five pits at coordinates 0, 1, 2, 3, and 4 on a number line, connected to Snuke's nest.
Now, N Snuke will appear from the pits. It is known that the i-th Snuke will appear from the pit at coordinate X_i at time T_i, and its size is A_i.
Takahashi is at coordinate 0 at time 0 and can move on the line at a speed of at most 1.
He can catch a Snuke appearing from a pit if and only if he is at the coordinate of that pit exactly when it appears.
The time it takes to catch a Snuke is negligible.
Find the maximum sum of the sizes of Snuke that Takahashi can catch by moving optimally.
Constraints
- 1 \leq N \leq 10^5
- 0 < T_1 < T_2 < \ldots < T_N \leq 10^5
- 0 \leq X_i \leq 4
- 1 \leq A_i \leq 10^9
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N T_1 X_1 A_1 T_2 X_2 A_2 \vdots T_N X_N A_N
Output
Print the answer as an integer.
Sample Input 1
3 1 0 100 3 3 10 5 4 1
Sample Output 1
101
The optimal strategy is as follows.
- Wait at coordinate 0 to catch the first Snuke at time 1.
- Go to coordinate 4 to catch the third Snuke at time 5.
It is impossible to catch both the first and second Snuke, so this is the best he can.
Sample Input 2
3 1 4 1 2 4 1 3 4 1
Sample Output 2
0
Takahashi cannot catch any Snuke.
Sample Input 3
10 1 4 602436426 2 1 623690081 3 3 262703497 4 4 628894325 5 3 450968417 6 1 161735902 7 1 707723857 8 2 802329211 9 0 317063340 10 2 125660016
Sample Output 3
2978279323