Problem Statement

You are given a sequence of length N consisting of integers: A=(A_1,\ldots,A_N).

Find the smallest non-negative integer not in (A_1,\ldots,A_N).

Constraints

• 1 \leq N \leq 2000
• 0 \leq A_i \leq 2000
• All values in input are integers.

Sample Input 1

8
0 3 2 6 2 1 0 0

Sample Output 1

4

The non-negative integers are 0,1,2,3,4,\ldots.
We have 0,1,2,3 in A, but not 4, so the answer is 4.

Sample Input 2

3
2000 2000 2000

Sample Output 2

0

Problem Statement

Keyence has N bases worldwide, numbered 1 to N. Base i has W_i employees, and at 0 o'clock in Coordinated Universal Time (UTC), it is X_i o'clock at base i.

You want to hold a one-hour meeting across the entire company. Each employee can only participate in the meeting if the meeting time is completely within the 9:00-18:00 time slot at their base. Find the maximum number of employees who can participate when deciding the meeting time to allow as many employees as possible to participate.

Constraints

• 1\leq N \leq 1000
• 1\leq W_i \leq 10^6
• 0\leq X_i < 24
• All input values are integers.

Sample Input 1

3
5 0
3 3
2 18

Sample Output 1

8

Consider holding the meeting from 14:00 to 15:00 in UTC.

• The meeting is held from 14:00 to 15:00 at base 1, so the 5 employees at base 1 can participate in the meeting.
• The meeting is held from 17:00 to 18:00 at base 2, so the 3 employees at base 2 can participate in the meeting.
• The meeting is held from 8:00 to 9:00 at base 3, so the 2 employees at base 3 cannot participate in the meeting.

Thus, a total of 5+3=8 employees can participate in the meeting. No meeting time allows more employees to participate.

Sample Input 2

2
1 10
1000000 20

Sample Output 2

1000000

Sample Input 3

6
31 3
20 8
11 5
4 3
47 14
1 18

Sample Output 3

67

Problem Statement

A region has N towns numbered 1 to N, and M roads numbered 1 to M.

The i-th road connects town A_i and town B_i bidirectionally with length C_i.

Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.

Constraints

• 2 \leq N \leq 10
• 1 \leq M \leq \frac{N(N-1)}{2}
• 1 \leq A_i < B_i \leq N
• The pairs (A_i,B_i) are distinct.
• 1\leq C_i \leq 10^8
• All input values are integers.

Sample Input 1

4 4
1 2 1
2 3 10
1 3 100
1 4 1000

Sample Output 1

1110

If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.

Sample Input 2

10 1
5 9 1

Sample Output 2

1

There may be a town that is not connected to a road.

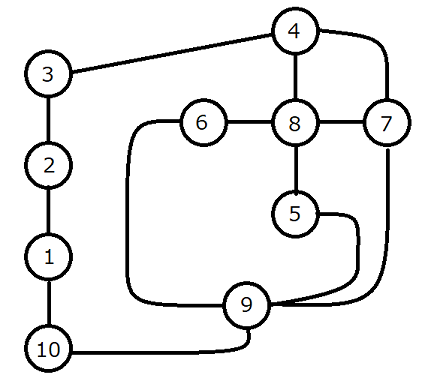
Sample Input 3

10 13
1 2 1
1 10 1
2 3 1
3 4 4
4 7 2
4 8 1
5 8 1
5 9 3
6 8 1
6 9 5
7 8 1
7 9 4
9 10 3

Sample Output 3

20

Problem Statement

Among the positive integers that consist of 0's and 2's when written in base 10, find the K-th smallest integer.

Constraints

• K is an integer between 1 and 10^{18} (inclusive).

Sample Input 1

3

Sample Output 1

22

The positive integers that consist of 0's and 2's when written in base 10 are 2,20,22,\dots in ascending order.
The (K=) 3-rd of them, which is 22, should be printed.

Sample Input 2

11

Sample Output 2

2022

Sample Input 3

923423423420220108

Sample Output 3

220022020000202020002022022000002020002222002200002022002200

Note that the exact value of the answer must be printed as an integer, even if it is big.

Problem Statement

Takahashi has N balls. Each ball has an integer not less than 2 written on it. He will insert them in a cylinder one by one. The integer written on the i-th ball is a_i.

The balls are made of special material. When k balls with k (k \geq 2) written on them line up in a row, all these k balls will disappear.

For each i (1 \leq i \leq N), find the number of balls after inserting the i-th ball.

Constraints

• 1 \leq N \leq 2 \times 10^5
• 2 \leq a_i \leq 2 \times 10^5 \, (1 \leq i \leq N)
• All values in input are integers.

Sample Input 1

5
3 2 3 2 2

Sample Output 1

1
2
3
4
3

The content of the cylinder changes as follows.

• After inserting the 1-st ball, the cylinder contains the ball with 3.
• After inserting the 2-nd ball, the cylinder contains 3, 2 from bottom to top.
• After inserting the 3-rd ball, the cylinder contains 3, 2, 3 from bottom to top.
• After inserting the 4-th ball, the cylinder contains 3, 2, 3, 2 from bottom to top.
• After inserting the 5-th ball, the cylinder momentarily has 3, 2, 3, 2, 2 from bottom to top. The two consecutive balls with 2 disappear, and the cylinder eventually contains 3, 2, 3 from bottom to top.

Sample Input 2

10
2 3 2 3 3 3 2 3 3 2

Sample Output 2

1
2
3
4
5
3
2
3
1
0