実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
A, B, C からなる長さ N の文字列 S が与えられます。
S の中で ABC が(連続な)部分文字列として初めて現れる位置を答えてください。すなわち、以下の条件を全て満たす整数 n のうち最小のものを答えてください。
- 1 \leq n \leq N - 2
- S の n 文字目から n+2 文字目までを取り出して出来る文字列は
ABCである。
ただし、ABC が S に現れない場合は -1 を出力してください。
制約
- 3 \leq N \leq 100
- S は
A,B,Cからなる長さ N の文字列
入力
入力は以下の形式で標準入力から与えられる。
N S
出力
S の中で ABC が部分文字列として初めて現れる位置を出力せよ。ただし、ABC が S に現れない場合は -1 を出力せよ。
入力例 1
8 ABABCABC
出力例 1
3
S の中で ABC が初めて現れるのは 3 文字目から 5 文字目までの位置です。よって 3 が答えになります。
入力例 2
3 ACB
出力例 2
-1
ABC が S に現れない場合は -1 を出力してください。
入力例 3
20 BBAAABBACAACABCBABAB
出力例 3
13
Score : 100 points
Problem Statement
You are given a string S of length N consisting of A, B, and C.
Find the position where ABC first appears as a (contiguous) substring in S. In other words, find the smallest integer n that satisfies all of the following conditions.
- 1 \leq n \leq N - 2.
- The string obtained by extracting the n-th through (n+2)-th characters of S is
ABC.
If ABC does not appear in S, print -1.
Constraints
- 3 \leq N \leq 100
- S is a string of length N consisting of
A,B, andC.
Input
The input is given from Standard Input in the following format:
N S
Output
Print the position where ABC first appears as a substring in S, or -1 if it does not appear in S.
Sample Input 1
8 ABABCABC
Sample Output 1
3
ABC first appears in S at the 3-rd through 5-th characters of S. Therefore, the answer is 3.
Sample Input 2
3 ACB
Sample Output 2
-1
If ABC does not appear in S, print -1.
Sample Input 3
20 BBAAABBACAACABCBABAB
Sample Output 3
13
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
0 以上 9999 以下の整数 N が与えられます。
N の先頭に必要なだけ 0 をつけ、4 桁の文字列にしたものを出力してください。
制約
- 0 \leq N \leq 9999
- N は整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを出力せよ。
入力例 1
321
出力例 1
0321
321 は 3 桁なので、先頭に 1 つ 0 をつけると 4 桁になります。
入力例 2
7777
出力例 2
7777
入力例 3
1
出力例 3
0001
Score : 100 points
Problem Statement
You are given an integer N between 0 and 9999 (inclusive).
Print it as a four-digit string after appending to it the necessary number of leading zeros.
Constraints
- 0 \leq N \leq 9999
- N is an integer.
Input
Input is given from Standard Input in the following format:
N
Output
Print the answer.
Sample Input 1
321
Sample Output 1
0321
321 has three digits, so we need to add one leading zero to it to make it have four digits.
Sample Input 2
7777
Sample Output 2
7777
Sample Input 3
1
Sample Output 3
0001
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
長さ N の正整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
A が等比数列であるか判定してください。
制約
- 2\leq N\leq 100
- 1\leq A_i\leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
A が 等比数列ならば Yes を、そうでないならば No を出力せよ。
入力例 1
5 3 6 12 24 48
出力例 1
Yes
A=(3,6,12,24,48) です。
A は初項 3, 公比 2, 項数 5 の等比数列となっています。
よって、Yes を出力します。
入力例 2
3 1 2 3
出力例 2
No
A=(1,2,3) です。
A_1:A_2=1:2\neq 2:3=A_2:A_3 より、A は等比数列ではありません。
よって、No を出力します。
入力例 3
2 10 8
出力例 3
Yes
A は初項 10, 公比 0.8, 項数 2 の等比数列となっています。
よって、Yes を出力します。
Score : 200 points
Problem Statement
You are given a length-N sequence A=(A_1,A_2,\ldots,A_N) of positive integers.
Determine whether A is a geometric progression.
Constraints
- 2 \leq N \leq 100
- 1 \leq A_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
If A is a geometric progression, print Yes; otherwise, print No.
Sample Input 1
5 3 6 12 24 48
Sample Output 1
Yes
A=(3,6,12,24,48).
A is a geometric progression with first term 3, common ratio 2, and five terms.
Therefore, print Yes.
Sample Input 2
3 1 2 3
Sample Output 2
No
A=(1,2,3).
Since A_1 : A_2 = 1 : 2 \neq 2 : 3 = A_2 : A_3, A is not a geometric progression.
Therefore, print No.
Sample Input 3
2 10 8
Sample Output 3
Yes
A is a geometric progression with first term 10, common ratio 0.8, and two terms.
Therefore, print Yes.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
1 から N の番号がついた N 人の人がいます。
人 i はキーエンス本社ビルの建築面積を S_i 平方メートルであると予想しました。
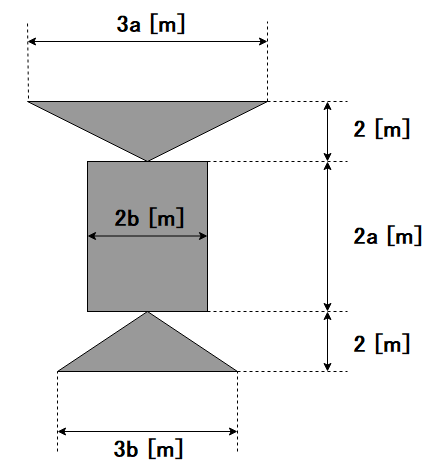
キーエンス本社ビルは下図のような形をしています。ただし、a,b はある 正の整数 です。
つまり、キーエンス本社ビルの建築面積は 4ab+3a+3b 平方メートルと表されます。
N 人のうち、この情報のみによって、予想した面積が確実に誤りであるとわかる人数を求めてください。
制約
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N S_1 \ldots S_N
出力
答えを出力せよ。
入力例 1
3 10 20 39
出力例 1
1
a=1,b=1 のとき面積は 10 平方メートル、a=2,b=3 のとき面積は 39 平方メートルとなります。
しかし a,b がどのような正の整数であったとしても面積が 20 平方メートルになることはありません。
よって、人 2 の予想だけは確実に誤りであることがわかります。
入力例 2
5 666 777 888 777 666
出力例 2
3
Score : 200 points
Problem Statement
There are N people numbered 1 to N.
Person i guessed the building area of KEYENCE headquarters building to be S_i square meters.
The shape of KEYENCE headquarters building is shown below, where a and b are some positive integers.
That is, the building area of the building can be represented as 4ab+3a+3b.
Based on just this information, how many of the N people are guaranteed to be wrong in their guesses?

Constraints
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N S_1 \ldots S_N
Output
Print the answer.
Sample Input 1
3 10 20 39
Sample Output 1
1
The area would be 10 square meters if a=1,b=1, and 39 square meters if a=2,b=3.
However, no pair of positive integers a and b would make the area 20 square meters.
Thus, we can only be sure that Person 2 guessed wrong.
Sample Input 2
5 666 777 888 777 666
Sample Output 2
3
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
英小文字のみからなる N 個の文字列 S_1,S_2,\dots,S_N が与えられます。
S_1,S_2,\dots,S_N から文字列を好きな個数選ぶことを考えます。
このとき、「選んだ文字列の中でちょうど K 個の文字列に登場する英小文字」の種類数としてあり得る最大値を求めてください。
制約
- 1 \le N \le 15
- 1 \le K \le N
- N,K は整数
- S_i は英小文字からなる空でない文字列である。
- 1 \le i \le N を満たす整数 i に対し、S_i に同じ文字は 2 個以上含まれない。
- i \neq j ならば S_i \neq S_j である。
入力
入力は以下の形式で標準入力から与えられる。
N K S_1 S_2 \vdots S_N
出力
答えを出力せよ。
入力例 1
4 2 abi aef bc acg
出力例 1
3
S_1,S_3,S_4 を選んだ場合、a,b,c がちょうど 2 個の文字列に含まれます。
4 個以上の文字がちょうど 2 個の文字列に含まれるような選び方は存在しないため、答えは 3 です。
入力例 2
2 2 a b
出力例 2
0
同じ文字列を複数回選ぶことはできません。
入力例 3
5 2 abpqxyz az pq bc cy
出力例 3
7
Score : 300 points
Problem Statement
You are given N strings S_1,S_2,\dots,S_N consisting of lowercase English alphabets.
Consider choosing some number of strings from S_1,S_2,\dots,S_N.
Find the maximum number of distinct alphabets that satisfy the following condition: "the alphabet is contained in exactly K of the chosen strings."
Constraints
- 1 \le N \le 15
- 1 \le K \le N
- N and K are integers.
- S_i is a non-empty string consisting of lowercase English alphabets.
- For each integer i such that 1 \le i \le N, S_i does not contain two or more same alphabets.
- If i \neq j, then S_i \neq S_j.
Input
Input is given from Standard Input in the following format:
N K S_1 S_2 \vdots S_N
Output
Print the answer.
Sample Input 1
4 2 abi aef bc acg
Sample Output 1
3
When S_1,S_3, and S_4 are chosen, a,b, and c occur in exactly two of the strings.
There is no way to choose strings so that 4 or more alphabets occur in exactly 2 of the strings, so the answer is 3.
Sample Input 2
2 2 a b
Sample Output 2
0
You cannot choose the same string more than once.
Sample Input 3
5 2 abpqxyz az pq bc cy
Sample Output 3
7