Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
チーム高橋とチーム青木が N 回の試合を行いました。 i 回め (1\leq i\leq N) の試合ではチーム高橋が X _ i 点、チーム青木が Y _ i 点を獲得しました。
N 回の試合で獲得した得点の合計がより多いチームの勝ちです。
どちらのチームが勝ったか出力してください。 ただし、獲得した得点の合計が等しい場合は引き分けとなります。
制約
- 1\leq N\leq 100
- 0\leq X _ i\leq 100\ (1\leq i\leq N)
- 0\leq Y _ i\leq 100\ (1\leq i\leq N)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N X _ 1 Y _ 1 X _ 2 Y _ 2 \vdots X _ N Y _ N
出力
チーム高橋が勝った場合 Takahashi を、チーム青木が勝った場合 Aoki を、引き分けの場合 Draw を出力せよ。
入力例 1
4 10 2 10 1 10 2 3 2
出力例 1
Takahashi
4 回の試合で、チーム高橋は 33 点、チーム青木は 7 点を獲得しました。
チーム高橋が勝ったため、Takahashi を出力してください。
入力例 2
6 5 4 4 5 2 4 1 6 7 1 3 2
出力例 2
Draw
いずれのチームも 22 点を獲得しました。
引き分けなので、Draw を出力してください。
入力例 3
4 0 0 10 10 50 50 0 100
出力例 3
Aoki
一方もしくは両方のチームが、一試合のうちに 1 点も取れない場合もあります。
Score: 100 points
Problem Statement
Team Takahashi and Team Aoki played N matches. In the i-th match (1\leq i\leq N), Team Takahashi scored X _ i points, and Team Aoki scored Y _ i points.
The team with the higher total score from the N matches wins.
Print the winner. If the two teams have the same total score, it is a draw.
Constraints
- 1\leq N\leq 100
- 0\leq X _ i\leq 100\ (1\leq i\leq N)
- 0\leq Y _ i\leq 100\ (1\leq i\leq N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X _ 1 Y _ 1 X _ 2 Y _ 2 \vdots X _ N Y _ N
Output
If Team Takahashi wins, print Takahashi; if Team Aoki wins, print Aoki; if it is a draw, print Draw.
Sample Input 1
4 10 2 10 1 10 2 3 2
Sample Output 1
Takahashi
In four matches, Team Takahashi scored 33 points, and Team Aoki scored 7 points.
Team Takahashi wins, so print Takahashi.
Sample Input 2
6 5 4 4 5 2 4 1 6 7 1 3 2
Sample Output 2
Draw
Both teams scored 22 points.
It is a draw, so print Draw.
Sample Input 3
4 0 0 10 10 50 50 0 100
Sample Output 3
Aoki
One or both teams may score no points in a match.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
英小文字からなる文字列 S が与えられます。
S に a が現れるならば最後に現れるのが何文字目かを出力し、現れないならば -1 を出力してください。
制約
- S は英小文字からなる長さ 1 以上 100 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
S
出力
答えを出力せよ。
入力例 1
abcdaxayz
出力例 1
7
S に a は 3 回現れますが、最後に現れるのは 7 文字目なので、7 を出力します。
入力例 2
bcbbbz
出力例 2
-1
S に a は現れないので、-1 を出力します。
入力例 3
aaaaa
出力例 3
5
Score : 100 points
Problem Statement
You are given a string S consisting of lowercase English letters.
If a appears in S, print the last index at which it appears; otherwise, print -1. (The index starts at 1.)
Constraints
- S is a string of length between 1 and 100 (inclusive) consisting of lowercase English letters.
Input
The input is given from Standard Input in the following format:
S
Output
Print the answer.
Sample Input 1
abcdaxayz
Sample Output 1
7
a appears three times in S. The last occurrence is at index 7, so you should print 7.
Sample Input 2
bcbbbz
Sample Output 2
-1
a does not appear in S, so you should print -1.
Sample Input 3
aaaaa
Sample Output 3
5
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
縦 8 マス、横 8 マスの 64 マスからなるマス目があります。 上から i 行目 (1\leq i\leq8) 、左から j 列目 (1\leq j\leq8) のマスをマス (i,j) と呼ぶことにします。
それぞれのマスは、空マスであるかコマが置かれているかのどちらかです。
マスの状態は長さ 8 の文字列からなる長さ 8 の列 (S _ 1,S _ 2,S _ 3,\ldots,S _ 8) で表されます。
マス (i,j) (1\leq i\leq8,1\leq j\leq8) は、S _ i の j 文字目が . のとき空マスで、# のときコマが置かれています。
あなたは、すでに置かれているどのコマにも取られないように、いずれかの空マスに自分のコマを置きたいです。
マス (i,j) に置かれているコマは、次のどちらかの条件を満たすコマを取ることができます。
- i 行目のマスに置かれている
- j 列目のマスに置かれている
たとえば、マス (4,4) に置かれているコマは、以下の図で青く示されたマスに置かれているコマを取ることができます。

あなたがコマを置くことができるマスがいくつあるか求めてください。
制約
- S _ i は
.,#からなる長さ 8 の文字列 (1\leq i\leq 8)
入力
入力は以下の形式で標準入力から与えられる。
S _ 1 S _ 2 S _ 3 S _ 4 S _ 5 S _ 6 S _ 7 S _ 8
出力
すでに置かれているコマに取られずに自分のコマを置くことができる空マスの個数を出力せよ。
入力例 1
...#.... #....... .......# ....#... .#...... ........ ........ ..#.....
出力例 1
4
すでに置かれているコマは、以下の図で青く示されたマスに置かれたコマを取ることができます。

よって、あなたがすでに置かれているコマに取られないように自分のコマを置くことができるマスはマス (6,6), マス (6,7), マス (7,6), マス (7,7) の 4 マスです。
入力例 2
........ ........ ........ ........ ........ ........ ........ ........
出力例 2
64
コマがひとつも置かれていないこともあります。
入力例 3
.#...... ..#..#.. ....#... ........ ..#....# ........ ...#.... ....#...
出力例 3
4
Score : 200 points
Problem Statement
There is a grid of 64 squares with 8 rows and 8 columns. Let (i,j) denote the square at the i-th row from the top (1\leq i\leq8) and j-th column from the left (1\leq j\leq8).
Each square is either empty or has a piece placed on it.
The state of the squares is represented by a sequence (S_1,S_2,S_3,\ldots,S_8) of 8 strings of length 8.
Square (i,j) (1\leq i\leq8,1\leq j\leq8) is empty if the j-th character of S_i is ., and has a piece if it is #.
You want to place your piece on an empty square in such a way that it cannot be captured by any of the existing pieces.
A piece placed on square (i,j) can capture pieces that satisfy either of the following conditions:
- Placed on a square in row i
- Placed on a square in column j
For example, a piece placed on square (4,4) can capture pieces placed on the squares shown in blue in the following figure:

How many squares can you place your piece on?
Constraints
- Each S_i is a string of length 8 consisting of
.and#(1\leq i\leq 8).
Input
The input is given from Standard Input in the following format:
S_1 S_2 S_3 S_4 S_5 S_6 S_7 S_8
Output
Print the number of empty squares where you can place your piece without it being captured by any existing pieces.
Sample Input 1
...#.... #....... .......# ....#... .#...... ........ ........ ..#.....
Sample Output 1
4
The existing pieces can capture pieces placed on the squares shown in blue in the following figure:

Therefore, you can place your piece without it being captured on 4 squares: square (6,6), square (6,7), square (7,6), and square (7,7).
Sample Input 2
........ ........ ........ ........ ........ ........ ........ ........
Sample Output 2
64
There may be no pieces on the grid.
Sample Input 3
.#...... ..#..#.. ....#... ........ ..#....# ........ ...#.... ....#...
Sample Output 3
4
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
長さ N の整数からなる数列 A=(A_1,\ldots,A_N) が与えられます。
A_1,\ldots,A_N に含まれない最小の非負整数を求めてください。
制約
- 1 \leq N \leq 2000
- 0 \leq A_i \leq 2000
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N A_1 \ldots A_N
出力
答えを出力せよ。
入力例 1
8 0 3 2 6 2 1 0 0
出力例 1
4
非負整数は 0,1,2,3,4,\ldots と続きます。
0,1,2,3 は A に含まれ、4 は A に含まれないので、答えは 4 です。
入力例 2
3 2000 2000 2000
出力例 2
0
Score : 200 points
Problem Statement
You are given a sequence of length N consisting of integers: A=(A_1,\ldots,A_N).
Find the smallest non-negative integer not in (A_1,\ldots,A_N).
Constraints
- 1 \leq N \leq 2000
- 0 \leq A_i \leq 2000
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N A_1 \ldots A_N
Output
Print the answer.
Sample Input 1
8 0 3 2 6 2 1 0 0
Sample Output 1
4
The non-negative integers are 0,1,2,3,4,\ldots.
We have 0,1,2,3 in A, but not 4, so the answer is 4.
Sample Input 2
3 2000 2000 2000
Sample Output 2
0
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
ある地方に、1 から N の番号がついた N 個の街と、1 から M の番号がついた M 本の道路があります。
i 番目の道路は街 A_i と街 B_i を双方向に結び、長さは C_i です。
好きな街からスタートして同じ街を二度以上通らずに別の街へ移動するときの、通る道路の長さの和としてありえる最大値を求めてください。
制約
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1\leq A_i < B_i \leq N
- (A_i,B_i) は相異なる
- 1\leq C_i \leq 10^8
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 C_1 \vdots A_M B_M C_M
出力
答えを出力せよ。
入力例 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
出力例 1
1110
4\to 1\to 3\to 2 と移動すると、通る道路の長さの和は 1110 となります。
入力例 2
10 1 5 9 1
出力例 2
1
道路と繋がっていない街が存在するかもしれません。
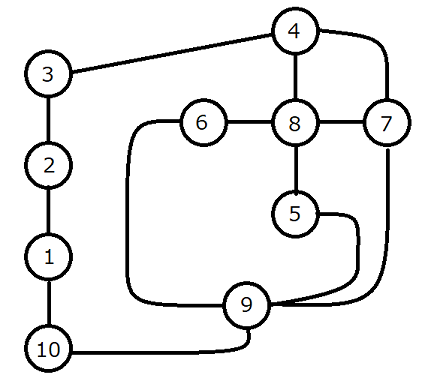
入力例 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
出力例 3
20
Score : 300 points
Problem Statement
A region has N towns numbered 1 to N, and M roads numbered 1 to M.
The i-th road connects town A_i and town B_i bidirectionally with length C_i.
Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.
Constraints
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1 \leq A_i < B_i \leq N
- The pairs (A_i,B_i) are distinct.
- 1\leq C_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 C_1 \vdots A_M B_M C_M
Output
Print the answer.
Sample Input 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
Sample Output 1
1110
If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.
Sample Input 2
10 1 5 9 1
Sample Output 2
1
There may be a town that is not connected to a road.
Sample Input 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
Sample Output 3
20
