Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
キーエンスでは、役割や年齢、立場の違いに関係なく「さん」付けして呼ぶという文化があります。
英小文字のみからなる文字列 S が与えられます。
S が san で終わっているならば Yes を、終わっていないならば No を出力してください。
制約
- S は英小文字のみからなる長さ 4 以上 30 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
S
出力
S が san で終わっているならば Yes を、終わっていないならば No を出力せよ。
入力例 1
takahashisan
出力例 1
Yes
文字列 S=takahashisan は san で終わっているため、 Yes を出力します。
入力例 2
aokikun
出力例 2
No
文字列 S=aokikun は san で終わっていないため、 No を出力します。
Score : 100 points
Problem Statement
KEYENCE has a culture of addressing everyone with the suffix "-san," regardless of roles, age, or positions.
You are given a string S consisting of lowercase English letters.
If S ends with san, print Yes; otherwise, print No.
Constraints
- S is a string of length between 4 and 30, inclusive, consisting of lowercase English letters.
Input
The input is given from Standard Input in the following format:
S
Output
If S ends with san, print Yes; otherwise, print No.
Sample Input 1
takahashisan
Sample Output 1
Yes
The string S= takahashisan ends with san, so print Yes.
Sample Input 2
aokikun
Sample Output 2
No
The string S= aokikun does not end with san, so print No.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
長さ N の正整数列 A=(A_1,A_2,\dots,A_N) が与えられます。
A の奇数番目の要素の総和を求めてください。すなわち、N 以下の最大の奇数を m としたとき A_1+A_3+A_5+\ldots+A_m を求めてください。
制約
- 1\leq N\leq 100
- 1\leq A_i\leq 100
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
答えを出力せよ。
入力例 1
7 3 1 4 1 5 9 2
出力例 1
14
A の奇数番目の要素の総和は A_1+A_3+A_5+A_7=3+4+5+2=14 です。
入力例 2
1 100
出力例 2
100
入力例 3
14 100 10 1 10 100 10 1 10 100 10 1 10 100 10
出力例 3
403
Score : 100 points
Problem Statement
You are given a sequence of positive integers of length N: A=(A_1,A_2,\dots,A_N).
Find the sum of the odd-indexed elements of A. That is, find A_1 + A_3 + A_5 + \dots + A_m, where m is the largest odd number not exceeding N.
Constraints
- 1 \le N \le 100
- 1 \le A_i \le 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \dots A_N
Output
Print the answer.
Sample Input 1
7 3 1 4 1 5 9 2
Sample Output 1
14
The sum of the odd-indexed elements of A is A_1+A_3+A_5+A_7=3+4+5+2=14.
Sample Input 2
1 100
Sample Output 2
100
Sample Input 3
14 100 10 1 10 100 10 1 10 100 10 1 10 100 10
Sample Output 3
403
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
高橋君はゲームの中で洞窟を探索しています。
洞窟は N 個の部屋が一列に並んだ構造であり、入り口から順に部屋 1,2,\ldots,N と番号がついています。
最初、高橋君は部屋 1 におり、持ち時間 は T です。
各 1 \leq i \leq N-1 について、持ち時間を A_i 消費することで、部屋 i から部屋 i+1 へ移動することができます。これ以外に部屋を移動する方法はありません。
また、持ち時間が 0 以下になるような移動は行うことができません。
洞窟内には M 個のボーナス部屋があります。i 番目のボーナス部屋は部屋 X_i であり、この部屋に到達すると持ち時間が Y_i 増加します。
高橋君は部屋 N にたどりつくことができますか?
制約
- 2 \leq N \leq 10^5
- 0 \leq M \leq N-2
- 1 \leq T \leq 10^9
- 1 \leq A_i \leq 10^9
- 1 < X_1 < \ldots < X_M < N
- 1 \leq Y_i \leq 10^9
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M T
A_1 A_2 \ldots A_{N-1}
X_1 Y_1
X_2 Y_2
\vdots
X_M Y_M
出力
高橋君が部屋 N にたどりつくことができるなら Yes を、できないなら No を出力せよ。
入力例 1
4 1 10 5 7 5 2 10
出力例 1
Yes
- 高橋君は最初、部屋 1 にいて持ち時間は 10 です。
- 持ち時間を 5 消費して部屋 2 に移動します。持ち時間は 5 になります。その後、持ち時間が 10 増え 15 になります。
- 持ち時間を 7 消費して部屋 3 に移動します。持ち時間は 8 になります。
- 持ち時間を 5 消費して部屋 4 に移動します。持ち時間は 3 になります。
入力例 2
4 1 10 10 7 5 2 10
出力例 2
No
部屋 1 から部屋 2 へ移動することができません。
Score : 200 points
Problem Statement
Takahashi is exploring a cave in a video game.
The cave consists of N rooms arranged in a row. The rooms are numbered Room 1,2,\ldots,N from the entrance.
Takahashi is initially in Room 1, and the time limit is T.
For each 1 \leq i \leq N-1, he may consume a time of A_i to move from Room i to Room (i+1). There is no other way to move between rooms.
He cannot make a move that makes the time limit 0 or less.
There are M bonus rooms in the cave. The i-th bonus room is Room X_i; when he arrives at the room, the time limit increases by Y_i.
Can Takahashi reach Room N?
Constraints
- 2 \leq N \leq 10^5
- 0 \leq M \leq N-2
- 1 \leq T \leq 10^9
- 1 \leq A_i \leq 10^9
- 1 < X_1 < \ldots < X_M < N
- 1 \leq Y_i \leq 10^9
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N M T
A_1 A_2 \ldots A_{N-1}
X_1 Y_1
X_2 Y_2
\vdots
X_M Y_M
Output
If Takahashi can reach Room N, print Yes; otherwise, print No.
Sample Input 1
4 1 10 5 7 5 2 10
Sample Output 1
Yes
- Takahashi is initially in Room 1, and the time limit is 10.
- He consumes a time of 5 to move to Room 2. Now the time limit is 5. Then, the time limit increases by 10; it is now 15.
- He consumes a time of 7 to move to Room 3. Now the time limit is 8.
- He consumes a time of 5 to move to Room 4. Now the time limit is 3.
Sample Input 2
4 1 10 10 7 5 2 10
Sample Output 2
No
He cannot move from Room 1 to Room 2.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
1 から N までの番号がついた N 個の数列が与えられます。
数列 i は、長さが L_i で j (1 \leq j \leq L_i) 番目の要素が a_{i,j} であるような数列です。
数列 i と 数列 j は、 L_i = L_j かつすべての k (1 \leq k \leq L_i) に対して a_{i,k} = a_{j,k} が成り立つ時に同じであるとみなします。
同じ数列は 1 種類として数えるとき、数列 1 から 数列 N の中に全部で何種類の数列がありますか?
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq L_i \leq 2 \times 10^5 (1 \leq i \leq N)
- 0 \leq a_{i,j} \leq 10^{9} (1 \leq i \leq N, 1 \leq j \leq L_i)
- すべての数列の要素の個数の和、すなわち \sum_{i=1}^N L_i は 2 \times 10^5 を超えない。
- 入力はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N
L_1 a_{1,1} a_{1,2} \dots a_{1,L_1}
L_2 a_{2,1} a_{2,2} \dots a_{2,L_2}
\vdots
L_N a_{N,1} a_{N,2} \dots a_{N,L_N}
出力
数列の種類数を出力せよ。
入力例 1
4 2 1 2 2 1 1 2 2 1 2 1 2
出力例 1
3
入力例 1 で与えられている数列は以下の 4 個です。
- 数列 1 : (1, 2)
- 数列 2 : (1, 1)
- 数列 3 : (2, 1)
- 数列 4 : (1, 2)
このうち数列 1 と数列 4 は同じ数列で、それ以外は互いに異なる数列なので全部で 3 種類の数列があります。
入力例 2
5 1 1 1 1 1 2 2 1 1 3 1 1 1
出力例 2
4
入力例 2 で与えられている数列は以下の 5 個です。
- 数列 1 : (1)
- 数列 2 : (1)
- 数列 3 : (2)
- 数列 4 : (1, 1)
- 数列 5 : (1, 1, 1)
入力例 3
1 1 1
出力例 3
1
Score : 200 points
Problem Statement
You are given N sequences numbered 1 to N.
Sequence i has a length of L_i and its j-th element (1 \leq j \leq L_i) is a_{i,j}.
Sequence i and Sequence j are considered the same when L_i = L_j and a_{i,k} = a_{j,k} for every k (1 \leq k \leq L_i).
How many different sequences are there among Sequence 1 through Sequence N?
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq L_i \leq 2 \times 10^5 (1 \leq i \leq N)
- 0 \leq a_{i,j} \leq 10^{9} (1 \leq i \leq N, 1 \leq j \leq L_i)
- The total number of elements in the sequences, \sum_{i=1}^N L_i, does not exceed 2 \times 10^5.
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N
L_1 a_{1,1} a_{1,2} \dots a_{1,L_1}
L_2 a_{2,1} a_{2,2} \dots a_{2,L_2}
\vdots
L_N a_{N,1} a_{N,2} \dots a_{N,L_N}
Output
Print the number of different sequences.
Sample Input 1
4 2 1 2 2 1 1 2 2 1 2 1 2
Sample Output 1
3
Sample Input 1 contains four sequences:
- Sequence 1 : (1, 2)
- Sequence 2 : (1, 1)
- Sequence 3 : (2, 1)
- Sequence 4 : (1, 2)
Except that Sequence 1 and Sequence 4 are the same, these sequences are pairwise different, so we have three different sequences.
Sample Input 2
5 1 1 1 1 1 2 2 1 1 3 1 1 1
Sample Output 2
4
Sample Input 2 contains five sequences:
- Sequence 1 : (1)
- Sequence 2 : (1)
- Sequence 3 : (2)
- Sequence 4 : (1, 1)
- Sequence 5 : (1, 1, 1)
Sample Input 3
1 1 1
Sample Output 3
1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
N 曲からなるプレイリストがあり、曲には 1, \dots, N の番号が付けられています。
曲 i の長さは A_i 秒です。
プレイリストを再生すると、曲 1、曲 2、\ldots、曲 N の順に流れます。曲 N が流れ終わると、再び曲 1 から順に流れていきます。ある曲の途中で次の曲が流れることはなく、曲が流れ終わると、その瞬間に次の曲が流れ始めます。
プレイリストを再生してから T 秒後に流れているのはどの曲ですか?また、その曲が流れ始めてから何秒の時点ですか?
ただし、T 秒後ちょうどに曲が切り替わるような入力は与えられません。
制約
- 1 \leq N \leq 10^5
- 1 \leq T \leq 10^{18}
- 1 \leq A_i \leq 10^9
- プレイリストを再生して T 秒後ちょうどに曲が切り替わることはない
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N T A_1 \ldots A_N
出力
プレイリストを再生してから T 秒後に流れている曲の番号と、その曲が流れ始めてから何秒たったかを表す整数を空白区切りで出力せよ。
入力例 1
3 600 180 240 120
出力例 1
1 60
プレイリストを再生してからの様子は次のようになります。
- 0 秒後から 180 秒後まで曲 1 が流れる。
- 180 秒後から 420 秒後まで曲 2 が流れる。
- 420 秒後から 540 秒後まで曲 3 が流れる。
- 540 秒後から 720 秒後まで曲 1 が流れる。
- 720 秒後から 960 秒後まで曲 2 が流れる。
- \qquad\vdots
600 秒後の時点で流れているのは曲 1 であり、流れ始めて 60 秒の時点です。
入力例 2
3 281 94 94 94
出力例 2
3 93
入力例 3
10 5678912340 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
出力例 3
6 678912340
Score : 300 points
Problem Statement
We have a playlist with N songs numbered 1, \dots, N.
Song i lasts A_i seconds.
When the playlist is played, song 1, song 2, \ldots, and song N play in this order. When song N ends, the playlist repeats itself, starting from song 1 again. While a song is playing, the next song does not play; when a song ends, the next song starts immediately.
At exactly T seconds after the playlist starts playing, which song is playing? Also, how many seconds have passed since the start of that song?
There is no input where the playlist changes songs at exactly T seconds after it starts playing.
Constraints
- 1 \leq N \leq 10^5
- 1 \leq T \leq 10^{18}
- 1 \leq A_i \leq 10^9
- The playlist does not change songs at exactly T seconds after it starts playing.
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N T A_1 \ldots A_N
Output
Print an integer representing the song that is playing at exactly T seconds after the playlist starts playing, and an integer representing the number of seconds that have passed since the start of that song, separated by a space.
Sample Input 1
3 600 180 240 120
Sample Output 1
1 60
When the playlist is played, the following happens. (Assume that it starts playing at time 0.)
- From time 0 to time 180, song 1 plays.
- From time 180 to time 420, song 2 plays.
- From time 420 to time 540, song 3 plays.
- From time 540 to time 720, song 1 plays.
- From time 720 to time 960, song 2 plays.
- \qquad\vdots
At time 600, song 1 is playing, and 60 seconds have passed since the start of that song.
Sample Input 2
3 281 94 94 94
Sample Output 2
3 93
Sample Input 3
10 5678912340 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
Sample Output 3
6 678912340
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
英小文字のみからなる長さ N の文字列 S = S_1S_2\ldots S_N が与えられます。
また、S に関する Q 個の質問が与えられます。 i = 1, 2, \ldots, Q について、i 番目の質問は 2 つの整数 l_i, r_i で表される下記の質問です。
S の l_i 文字目から r_i 文字目までからなる部分文字列 S_{l_i}S_{l_i+1}\ldots S_{r_i} において、 同じ英小文字が 2 つ隣りあう箇所は何個ありますか? すなわち、l_i \leq p \leq r_i-1 かつ S_p = S_{p+1}を満たす整数 p は何個ありますか?
Q 個の質問それぞれの答えを出力してください。
制約
- N, Q は整数
- 1 \leq N, Q \leq 3 \times 10^5
- S は英小文字のみからなる長さ N の文字列
- l_i, r_i は整数
- 1 \leq l_i \leq r_i \leq N
入力
入力は以下の形式で標準入力から与えられる。
N Q S l_1 r_1 l_2 r_2 \vdots l_Q r_Q
出力
Q 行出力せよ。 i = 1, 2, \ldots, Q について、i 行目には i 番目の質問に対する答えを出力せよ。
入力例 1
11 4 mississippi 3 9 4 10 4 6 7 7
出力例 1
2 2 0 0
4 個の質問それぞれに対する答えは下記の通りです。
- 1 個目の質問に関して、S_3S_4\ldots S_9 =
ssissipで同じ英小文字が隣り合う箇所は、S_3S_4 =ssと S_6S_7 =ssの 2 個です。 - 2 個目の質問に関して、S_4S_5\ldots S_{10} =
sissippで同じ英小文字が隣り合う箇所は、S_6S_7 =ssと S_9S_{10} =ppの 2 個です。 - 3 個目の質問に関して、S_4S_5S_6 =
sisで同じ英小文字が隣り合う箇所は 0 個です。 - 4 個目の質問に関して、S_7 =
sで同じ英小文字が隣り合う箇所は 0 個です。
入力例 2
5 1 aaaaa 1 5
出力例 2
4
S_1S_2\ldots S_5 = aaaaa で同じ英小文字が隣り合う箇所は、
S_1S_2 = aa 、S_2S_3 = aa 、S_3S_4 = aa 、S_4S_5 = aa の 4 個です。
Score : 300 points
Problem Statement
You are given a string S = S_1S_2\ldots S_N of length N consisting of lowercase English letters.
Additionally, you are given Q queries about the string S. For i = 1, 2, \ldots, Q, the i-th query is represented by two integers l_i, r_i and asks the following.
In the substring S_{l_i}S_{l_i+1}\ldots S_{r_i} of S, which ranges from the l_i-th to the r_i-th character, how many places are there where the same lowercase English letter occurs twice in a row? In other words, how many integers p satisfy l_i \leq p \leq r_i-1 and S_p = S_{p+1}?
Print the answer for each of the Q queries.
Constraints
- N and Q are integers.
- 1 \leq N, Q \leq 3 \times 10^5
- S is a string of length N consisting of lowercase English letters.
- l_i and r_i are integers.
- 1 \leq l_i \leq r_i \leq N
Input
The input is given from Standard Input in the following format:
N Q S l_1 r_1 l_2 r_2 \vdots l_Q r_Q
Output
Print Q lines. For i = 1, 2, \ldots, Q, the i-th line should contain the answer to the i-th query.
Sample Input 1
11 4 mississippi 3 9 4 10 4 6 7 7
Sample Output 1
2 2 0 0
The answers to the four queries are as follows.
- For the first query, S_3S_4\ldots S_9 =
ssissiphas two places where the same lowercase English letter occurs twice in a row: S_3S_4 =ssand S_6S_7 =ss. - For the second query, S_4S_5\ldots S_{10} =
sissipphas two places where the same lowercase English letter occurs twice in a row: S_6S_7 =ssand S_9S_{10} =pp. - For the third query, S_4S_5S_6 =
sishas zero places where the same lowercase English letter occurs twice in a row. - For the fourth query, S_7 =
shas zero places where the same lowercase English letter occurs twice in a row.
Sample Input 2
5 1 aaaaa 1 5
Sample Output 2
4
S_1S_2\ldots S_5 = aaaaa has four places where the same lowercase English letter occurs twice in a row:
S_1S_2 = aa, S_2S_3 = aa, S_3S_4 = aa, and S_4S_5 = aa.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
無限に広いグリッドがあります。グリッドのあるマスはマス (0,0) と名前がついています。
マス (0,0) から下に r マス、右に c マスの移動した位置にあるマスをマス (r,c) と呼びます。
ここで、「下に r マス移動する」は r が負のときは「上に |r| マス移動する」ことを表し、「右に c マス移動する」は c が負のときには「左に |c| マス移動する」ことを表すものとします。
具体的には、マス (0,0) の周辺にあるマスは以下のようになります。
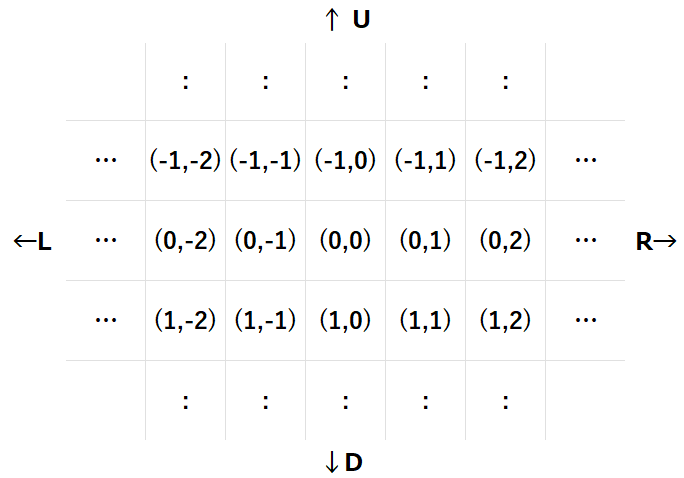
最初、高橋君はマス (R_t,C_t) に、青木君はマス (R_a,C_a) にいます。二人はそれぞれ U,D,L,R からなる長さ N の文字列 S,T に従って N 回移動を行います。
各 i について、高橋君と青木君の i 回目の移動は同時に行われます。具体的には、高橋君は S の i 文字目が U のとき上、D のとき下、L のとき左、R のとき右へ 1 マス移動し、青木君は T の i 文字目によって同様に移動します。
N 回の移動の中で、移動直後に高橋君と青木君が同じマスにいた回数を求めてください。
ただし、N は非常に大きいため S,T は ( (S'_1, A_1),\ldots(S'_M,A_M) ), ( (T'_1,B_1),\ldots,(T'_L,B_L) ) の形で与えられ、 S は「文字 S'_1 を A_1 個、\dots、文字 S'_M を A_M 個」をこの順に連結した文字列であり、T も同様です。
制約
- -10^9 \leq R_t,C_t,R_a,C_a \leq 10^9
- 1\leq N \leq 10^{14}
- 1\leq M,L \leq 10^5
- S'_i,T'_i は
U,D,L,Rのいずれか - 1 \leq A_i,B_i \leq 10^9
- A_1+\dots+A_M=B_1+\dots+B_L=N
- 与えられる数値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
R_t C_t R_a C_a N M L S'_1 A_1 \vdots S'_M A_M T'_1 B_1 \vdots T'_L B_L
出力
答えを出力せよ。
入力例 1
0 0 4 2 3 2 1 R 2 D 1 U 3
出力例 1
1
このケースでは S= RRD、T= UUU であり、移動は次のように行われます。
- 最初、高橋君はマス (0,0) に、青木君はマス (4,2) にいる。
- 1 回目の移動後、高橋君はマス (0,1)、青木君はマス (3,2) にいる。
- 2 回目の移動後、高橋君はマス (0,2)、青木君はマス (2,2) にいる。
- 3 回目の移動後、高橋君はマス (1,2)、青木君はマス (1,2) にいる。
よって、高橋君と青木君が移動直後に同じマスにいた回数は 1 です。
入力例 2
1000000000 1000000000 -1000000000 -1000000000 3000000000 3 3 L 1000000000 U 1000000000 U 1000000000 D 1000000000 R 1000000000 U 1000000000
出力例 2
1000000001
2000000000 回目の移動から 3000000000 回目の移動までの 1000000001 回で高橋君と青木君は移動直後に同じマスにいます。
入力例 3
3 3 3 2 1 1 1 L 1 R 1
出力例 3
0
入力例 4
0 0 0 0 1 1 1 L 1 R 1
出力例 4
0
Score : 425 points
Problem Statement
There is an infinitely large grid. One cell of the grid is named cell (0,0).
The cell located r cells down and c cells right from cell (0,0) is called cell (r,c).
Here, "r cells down" means "|r| cells up" when r is negative, and "c cells right" means "|c| cells left" when c is negative.
Specifically, the cells around cell (0,0) are as follows:

Initially, Takahashi is at cell (R_t,C_t) and Aoki is at cell (R_a,C_a). They will each make N moves according to strings S and T of length N consisting of U, D, L, R.
For each i, Takahashi's and Aoki's i-th moves occur simultaneously: Takahashi moves one cell up if the i-th character of S is U, down if D, left if L, and right if R; Aoki moves similarly according to the i-th character of T.
Find the number of times Takahashi and Aoki are at the same cell immediately after a move during the N moves.
Since N is very large, S and T are given in the form ((S'_1, A_1),\ldots,(S'_M,A_M)) and ((T'_1,B_1),\ldots,(T'_L,B_L)), where S is the string obtained by concatenating "A_1 copies of character S'_1, \dots, A_M copies of character S'_M" in this order, and T is given similarly.
Constraints
- -10^9 \leq R_t,C_t,R_a,C_a \leq 10^9
- 1\leq N \leq 10^{14}
- 1\leq M,L \leq 10^5
- Each of S'_i and T'_i is one of
U,D,L,R. - 1 \leq A_i,B_i \leq 10^9
- A_1+\dots+A_M=B_1+\dots+B_L=N
- All given values are integers.
Input
The input is given from Standard Input in the following format:
R_t C_t R_a C_a N M L S'_1 A_1 \vdots S'_M A_M T'_1 B_1 \vdots T'_L B_L
Output
Print the answer.
Sample Input 1
0 0 4 2 3 2 1 R 2 D 1 U 3
Sample Output 1
1
In this case, S= RRD and T= UUU, and the movements proceed as follows:
- Initially, Takahashi is at cell (0,0) and Aoki is at cell (4,2).
- After the 1st move, Takahashi is at cell (0,1) and Aoki is at cell (3,2).
- After the 2nd move, Takahashi is at cell (0,2) and Aoki is at cell (2,2).
- After the 3rd move, Takahashi is at cell (1,2) and Aoki is at cell (1,2).
Thus, the number of times Takahashi and Aoki are at the same cell immediately after a move is 1.
Sample Input 2
1000000000 1000000000 -1000000000 -1000000000 3000000000 3 3 L 1000000000 U 1000000000 U 1000000000 D 1000000000 R 1000000000 U 1000000000
Sample Output 2
1000000001
From the 2000000000-th move to the 3000000000-th move, Takahashi and Aoki are at the same cell immediately after a move for 1000000001 times.
Sample Input 3
3 3 3 2 1 1 1 L 1 R 1
Sample Output 3
0
Sample Input 4
0 0 0 0 1 1 1 L 1 R 1
Sample Output 4
0
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
AtCoder スキー場には広場 1 、広場 2 、\ldots 、広場 N の N 個の広場があり、広場 i の標高は H_i です。 また、2 つの広場を双方向に結ぶ M 本の坂があり、i (1 \leq i \leq M) 本目の坂は広場 U_i と広場 V_i を双方向に結んでいます。どの 2 つの広場の間もいくつかの坂を使って移動することができます。
高橋君は坂を使うことによってのみ広場の間を移動でき、坂を通るごとに楽しさが変化します。具体的には広場 X と広場 Y を直接結ぶ坂を使って広場 X から広場 Y まで移動したとき次のように楽しさが変化します。
- 広場 X が広場 Y より標高が真に高い場合、その標高差、すなわち H_X-H_Y だけ楽しさが増加する。
- 広場 X が広場 Y より標高が真に低い場合、その標高差の 2 倍、すなわち 2(H_Y-H_X) だけ楽しさが減少する。
- 広場 X と広場 Y の標高が等しい場合、楽しさは変化しない。
楽しさは負の値になることもあります。
最初、高橋君は広場 1 におり、楽しさは 0 です。 高橋君はいくつかの坂( 0 本でも良い)を移動した後に好きな広場で行動を終えることができるとしたとき、行動を終えた時点の高橋君の楽しさとしてありうる最大の値を求めてください。
制約
- 2 \leq N \leq 2\times 10^5
- N-1 \leq M \leq \min( 2\times 10^5,\frac{N(N-1)}{2})
- 0 \leq H_i\leq 10^8 (1 \leq i \leq N)
- 1 \leq U_i < V_i \leq N (1 \leq i \leq M)
- i \neq j ならば (U_i,V_i) \neq (U_j, V_j)
- 入力はすべて整数である。
- どの 2 つの広場の間もいくつかの坂を使って移動することができる。
入力
入力は以下の形式で標準入力から与えられる。
N M H_1 H_2 \ldots H_N U_1 V_1 U_2 V_2 \vdots U_M V_M
出力
答えを出力せよ。
入力例 1
4 4 10 8 12 5 1 2 1 3 2 3 3 4
出力例 1
3
広場 1 \to 広場 3 \to 広場 4 と移動したとき、楽しさは次のように変化します。
- 広場 1(標高 10 )から坂を使って広場 3(標高 12 )へ移動します。楽しさは 2\times (12-10)=4 だけ減少し、0-4=-4 になります。
- 広場 3(標高 12 )から坂を使って広場 4(標高 5 )へ移動します。楽しさは 12-5=7 だけ増加し、-4+7=3 になります。
ここで行動を終了したとき終了時の楽しさは 3 であり、このときが最大となります。
入力例 2
2 1 0 10 1 2
出力例 2
0
一度も移動を行わない時、楽しさが最大となります。
Score : 500 points
Problem Statement
AtCoder Ski Area has N open spaces called Space 1, Space 2, \ldots, Space N. The altitude of Space i is H_i. There are M slopes that connect two spaces bidirectionally. The i-th slope (1 \leq i \leq M) connects Space U_i and Space V_i. It is possible to travel between any two spaces using some slopes.
Takahashi can only travel between spaces by using slopes. Each time he goes through a slope, his happiness changes. Specifically, when he goes from Space X to Space Y by using the slope that directly connects them, his happiness changes as follows.
- If the altitude of Space X is strictly higher than that of Space Y, the happiness increases by their difference: H_X-H_Y.
- If the altitude of Space X is strictly lower than that of Space Y, the happiness decreases by their difference multiplied by 2: 2(H_Y-H_X).
- If the altitude of Space X is equal to that of Space Y, the happiness does not change.
The happiness may be a negative value.
Initially, Takahashi is in Space 1, and his happiness is 0. Find his maximum possible happiness after going through any number of slopes (possibly zero), ending in any space.
Constraints
- 2 \leq N \leq 2\times 10^5
- N-1 \leq M \leq \min( 2\times 10^5,\frac{N(N-1)}{2})
- 0 \leq H_i\leq 10^8 (1 \leq i \leq N)
- 1 \leq U_i < V_i \leq N (1 \leq i \leq M)
- (U_i,V_i) \neq (U_j, V_j) if i \neq j.
- All values in input are integers.
- It is possible to travel between any two spaces using some slopes.
Input
Input is given from Standard Input in the following format:
N M H_1 H_2 \ldots H_N U_1 V_1 U_2 V_2 \vdots U_M V_M
Output
Print the answer.
Sample Input 1
4 4 10 8 12 5 1 2 1 3 2 3 3 4
Sample Output 1
3
If Takahashi takes the route Space 1 \to Space 3 \to Space 4, his happiness changes as follows.
- When going from Space 1 (altitude 10) to Space 3 (altitude 12), it decreases by 2\times (12-10)=4 and becomes 0-4=-4.
- When going from Space 3 (altitude 12) to Space 4 (altitude 5), it increases by 12-5=7 and becomes -4+7=3.
If he ends the travel here, the final happiness will be 3, which is the maximum possible value.
Sample Input 2
2 1 0 10 1 2
Sample Output 2
0
His happiness is maximized by not moving at all.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 575 点
問題文
数直線上に 1 体のタコ型ロボットと N 個の宝があります。
i (1\leq i\leq N) 個目の宝はそれぞれ座標 X_i にあります。
タコ型ロボットは 1 つの頭と N 本の足を持っており、i 本目の足の長さは L_i (1\leq i\leq N) です。
タコ型ロボットが次のようにして N 個の宝すべてを掴む事ができるような整数 k の個数を求めてください。
- 頭を座標 k におく。
- i=1,2,\ldots,N の順に、「頭から距離 L_i 以下の範囲、すなわち k-L_i\leq x\leq k+L_i をみたす座標 x にまだ掴んでいない宝が存在する場合、そのうちの 1 つを選んで掴む」ことを繰り返す。
制約
- 1 \leq N\leq 200
- -10^{18} \leq X_1<X_2<\cdots<X_N\leq 10^{18}
- 1\leq L_1\leq L_2\leq\cdots\leq L_N\leq 10^{18}
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N X_1 X_2 \ldots X_N L_1 L_2 \ldots L_N
出力
問題文の条件をみたす整数 k の個数を出力せよ。
入力例 1
3 -6 0 7 3 5 10
出力例 1
6
k=-3,-2,-1,2,3,4 が条件をみたします。例えば、k=-3 のときは、次のようにして 3 個の宝をすべて掴む事ができます。
- 1 本目の足は -6\leq x\leq 0 にある宝を掴む事ができる。このうち座標 -6 にある 1 個目の宝を掴む。
- 2 本目の足は -8\leq x\leq 2 にある宝を掴む事ができる。このうち座標 0 にある 2 個目の宝を掴む。
- 3 本目の足は -13\leq x\leq 7 にある宝を掴む事ができる。このうち座標 7 にある 3 個目の宝を掴む。
入力例 2
1 0 1000000000000000000
出力例 2
2000000000000000001
-10^{18} 以上 10^{18} 以下のすべての整数が k として条件をみたします。
入力例 3
2 -100 100 1 1
出力例 3
0
条件をみたす k は存在しません。
Score : 575 points
Problem Statement
There is an octopus-shaped robot and N treasures on a number line.
The i-th treasure (1\leq i\leq N) is located at coordinate X_i.
The robot has one head and N legs, and the i-th leg (1\leq i\leq N) has a length of L_i.
Find the number of integers k such that the robot can grab all N treasures as follows.
- Place the head at coordinate k.
- Repeat the following for i=1,2,\ldots,N in this order: if there is a treasure that has not been grabbed yet within a distance of L_i from the head, that is, at a coordinate x satisfying k-L_i\leq x\leq k+L_i, choose one such treasure and grab it.
Constraints
- 1 \leq N\leq 200
- -10^{18} \leq X_1<X_2<\cdots<X_N\leq 10^{18}
- 1\leq L_1\leq L_2\leq\cdots\leq L_N\leq 10^{18}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X_1 X_2 \ldots X_N L_1 L_2 \ldots L_N
Output
Print the number of integers k that satisfy the condition in the statement.
Sample Input 1
3 -6 0 7 3 5 10
Sample Output 1
6
k=-3,-2,-1,2,3,4 satisfy the condition. For example, when k=-3, the robot can grab all three treasures as follows.
- The first leg can grab treasures at coordinates x satisfying -6\leq x\leq 0. Among them, grab the first treasure at coordinate -6.
- The second leg can grab treasures at coordinates x satisfying -8\leq x\leq 2. Among them, grab the second treasure at coordinate 0.
- The third leg can grab treasures at coordinates x satisfying -13\leq x\leq 7. Among them, grab the third treasure at coordinate 7.
Sample Input 2
1 0 1000000000000000000
Sample Output 2
2000000000000000001
All integers k from -10^{18} to 10^{18} satisfy the condition.
Sample Input 3
2 -100 100 1 1
Sample Output 3
0
No k satisfies the conditions.