Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
AtCoder 市では市長選挙が行われています。候補者は高橋氏と青木氏です。
2 人のどちらかに投じられた有効票は N 票あり、現在開票が行われています。なお、 N は奇数です。
現在の開票作業の途中経過は高橋氏に T 票、青木氏に A 票です。
現時点で勝敗が確定しているかを判定してください。
制約
- 1 \leq N \leq 99
- N は奇数
- 0 \leq T,A \leq N
- T+A \leq N
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N T A
出力
現時点で勝敗が確定しているならば Yes 、そうでなければ No と出力せよ。
入力例 1
7 4 2
出力例 1
Yes
残りの 1 票が青木氏に入っても、高橋氏は勝利します。高橋氏の勝利が確定しているため、Yes と出力します。
入力例 2
99 12 48
出力例 2
No
現時点では青木氏が多く票を獲得していますが、高橋氏が残りの 39 票を獲得すると高橋氏が勝利します。よって、No と出力します。
入力例 3
1 0 0
出力例 3
No
Score : 100 points
Problem Statement
A mayoral election is being held in AtCoder City. The candidates are Takahashi and Aoki.
There are N valid votes cast for either of the two candidates, and the counting is currently underway. Here, N is an odd number.
The current vote count is T votes for Takahashi and A votes for Aoki.
Determine if the outcome of the election is already decided at this point.
Constraints
- 1 \leq N \leq 99
- N is an odd number.
- 0 \leq T, A \leq N
- T + A \leq N
- All input values are integers.
Input
The input is given from standard input in the following format:
N T A
Output
Print Yes if the outcome of the election is already decided, and No otherwise.
Sample Input 1
7 4 2
Sample Output 1
Yes
Even if the remaining one vote goes to Aoki, Takahashi will still win. That is, his victory is decided, so print Yes.
Sample Input 2
99 12 48
Sample Output 2
No
Although Aoki currently has more votes, Takahashi would win if he receives the remaining 39 votes. Therefore, print No.
Sample Input 3
1 0 0
Sample Output 3
No
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
1 から N までの番号が付けられた N 人の人がいます。 それぞれの人にはプログラミング力という整数値が定まっており、人 i のプログラミング力は P_i です。 人 1 が最強になるためには、あといくつプログラミング力を上げる必要がありますか? すなわち、すべての i \neq 1 に対して P_1 + x > P_i を満たすような最小の非負整数 x は何ですか?
制約
- 1\leq N \leq 100
- 1\leq P_i \leq 100
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N P_1 P_2 \dots P_N
出力
答えを整数として出力せよ。
入力例 1
4 5 15 2 10
出力例 1
11
人 1 が最強になるためには、プログラミング力を 16 以上にする必要があります。 よって、答えは 16-5=11 です。
入力例 2
4 15 5 2 10
出力例 2
0
人 1 は既に最強なので、これ以上プログラミング力を上げる必要はありません。
入力例 3
3 100 100 100
出力例 3
1
Score : 100 points
Problem Statement
There are N people numbered 1 through N. Each person has a integer score called programming ability; person i's programming ability is P_i points. How many more points does person 1 need, so that person 1 becomes the strongest? In other words, what is the minimum non-negative integer x such that P_1 + x > P_i for all i \neq 1?
Constraints
- 1\leq N \leq 100
- 1\leq P_i \leq 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N P_1 P_2 \dots P_N
Output
Print the answer as an integer.
Sample Input 1
4 5 15 2 10
Sample Output 1
11
Person 1 becomes the strongest when their programming skill is 16 points or more, so the answer is 16-5=11.
Sample Input 2
4 15 5 2 10
Sample Output 2
0
Person 1 is already the strongest, so no more programming skill is needed.
Sample Input 3
3 100 100 100
Sample Output 3
1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
N 行 N 列のマス目が与えられます。上から i 行目、左から j 列目のマスには整数 A_{i,j} が書かれています。ここで、A_{i,j} は 0 か 1 であることが保証されます。
マス目の外側のマスに書かれた整数を時計回りに 1 個ずつずらしたときのマス目を出力してください。
ただし外側のマスとは、1 行目、N 行目、1 列目、N 列目のいずれか 1 つ以上に属するマスの集合のことを指します。
制約
- 2 \le N \le 100
- 0 \le A_{i,j} \le 1(1 \le i,j \le N)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
A_{1,1}A_{1,2}\dots A_{1,N}
A_{2,1}A_{2,2}\dots A_{2,N}
\vdots
A_{N,1}A_{N,2}\dots A_{N,N}
出力
マス目の外側のマスに書かれた整数を時計回りに 1 個ずつずらしたときのマス目において、上から i 行目、左から j 列目のマスに書かれている整数を B_{i,j} と置く。このとき、以下の形式で出力せよ。
B_{1,1}B_{1,2}\dots B_{1,N}
B_{2,1}B_{2,2}\dots B_{2,N}
\vdots
B_{N,1}B_{N,2}\dots B_{N,N}
入力例 1
4 0101 1101 1111 0000
出力例 1
1010 1101 0111 0001
上から i 行目、左から j 列目のマスを (i,j) と呼ぶこととします。
外側のマスは (1,1) から時計回りに列挙すると (1,1),(1,2),(1,3),(1,4),(2,4),(3,4),(4,4),(4,3),(4,2),(4,1),(3,1),(2,1) の 12 個です。
これらのマスに書かれている整数を、時計回りに 1 個ずつ動かすと出力欄のようになります。
入力例 2
2 11 11
出力例 2
11 11
入力例 3
5 01010 01001 10110 00110 01010
出力例 3
00101 11000 00111 00110 10100
Score : 200 points
Problem Statement
You are given a grid with N rows and N columns. An integer A_{i, j} is written on the square at the i-th row from the top and j-th column from the left. Here, it is guaranteed that A_{i,j} is either 0 or 1.
Shift the integers written on the outer squares clockwise by one square each, and print the resulting grid.
Here, the outer squares are those in at least one of the 1-st row, N-th row, 1-st column, and N-th column.
Constraints
- 2 \le N \le 100
- 0 \le A_{i,j} \le 1(1 \le i,j \le N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
A_{1,1}A_{1,2}\dots A_{1,N}
A_{2,1}A_{2,2}\dots A_{2,N}
\vdots
A_{N,1}A_{N,2}\dots A_{N,N}
Output
Let B_{i,j} be the integer written on the square at the i-th row from the top and j-th column from the left in the grid resulting from shifting the outer squares clockwise by one square each. Print them in the following format:
B_{1,1}B_{1,2}\dots B_{1,N}
B_{2,1}B_{2,2}\dots B_{2,N}
\vdots
B_{N,1}B_{N,2}\dots B_{N,N}
Sample Input 1
4 0101 1101 1111 0000
Sample Output 1
1010 1101 0111 0001
We denote by (i,j) the square at the i-th row from the top and j-th column from the left.
The outer squares, in clockwise order starting from (1,1), are the following 12 squares: (1,1),(1,2),(1,3),(1,4),(2,4),(3,4),(4,4),(4,3),(4,2),(4,1),(3,1), and (2,1).
The sample output shows the resulting grid after shifting the integers written on those squares clockwise by one square.
Sample Input 2
2 11 11
Sample Output 2
11 11
Sample Input 3
5 01010 01001 10110 00110 01010
Sample Output 3
00101 11000 00111 00110 10100
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
人 1 、人 2 、\ldots 、人 N と番号をつけられた N 人の人がいます。
N 人は、人 1 、人 2 、\ldots 、人 N の順番に下記の行動をちょうど 1 回ずつ行います。
- 人 i 自身がまだ一度も番号を呼ばれていないなら、人 A_i の番号を呼ぶ。
最後まで番号を一度も呼ばれない人全員の番号を昇順に列挙してください。
制約
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i \leq N
- A_i \neq i
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
下記の形式にしたがって、最後まで番号を一度も呼ばれない人全員の番号を昇順に列挙せよ。
K X_1 X_2 \ldots X_K
すなわち、まず 1 行目に、最後まで番号を一度も呼ばれない人の人数 K を出力し、 2 行目に、最後まで番号を一度も呼ばれない人全員の番号を昇順に並べた列 (X_1, X_2, \ldots, X_K) を空白区切りで出力せよ。
入力例 1
5 3 1 4 5 4
出力例 1
2 2 4
5 人の行動は下記の通りです。
- 人 1 はまだ番号を一度も呼ばれていないので、人 1 は人 3 の番号を呼びます。
- 人 2 はまだ番号を一度も呼ばれていないので、人 2 は人 1 の番号を呼びます。
- 人 3 はすでに人 1 によって番号を呼ばれているので、何もしません。
- 人 4 はまだ番号を一度も呼ばれていないので、人 4 は人 5 の番号を呼びます。
- 人 5 はすでに人 4 によって番号を呼ばれているので、何もしません。
よって、最後まで番号を一度も呼ばれないのは人 2 と人 4 です。
入力例 2
20 9 7 19 7 10 4 13 9 4 8 10 15 16 3 18 19 12 13 2 12
出力例 2
10 1 2 5 6 8 11 14 17 18 20
Score : 200 points
Problem Statement
There are N people whose IDs are 1, 2, \ldots, and N.
Each of person 1, person 2, \ldots, and person N performs the following action once in this order:
- If person i's ID has not been called out yet, call out person A_i's ID.
Enumerate the IDs of all the people whose IDs are never called out until the end in ascending order.
Constraints
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i \leq N
- A_i \neq i
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Enumerate the IDs of all the people whose IDs are not called out until the end in ascending order in the following format:
K X_1 X_2 \ldots X_K
In other words, the first line should contain the number of people, K, whose IDs are never called out until the end; the second line should contain the sequence (X_1, X_2, \ldots, X_K) of IDs of such people in ascending order, with spaces in between.
Sample Input 1
5 3 1 4 5 4
Sample Output 1
2 2 4
The five people's actions are as follows.
- Person 1's ID has not been called out yet, so person 1 calls out person 3's ID.
- Person 2's ID has not been called out yet, so person 2 calls out person 1's ID.
- Person 3's ID has already been called out by person 1, so nothing happens.
- Person 4's ID has not been called out yet, so person 4 calls out person 5's ID.
- Person 5's ID has already been called out by person 4, so nothing happens.
Therefore, person 2 and 4's IDs are not called out until the end.
Sample Input 2
20 9 7 19 7 10 4 13 9 4 8 10 15 16 3 18 19 12 13 2 12
Sample Output 2
10 1 2 5 6 8 11 14 17 18 20
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
高橋くんは、カードゲーム「AtCoder Magics」のカードを N 枚持っています。i 番目のカードをカード i と呼ぶことにします。各カードには強さとコストのパラメーターがあり、カード i の強さは A_i で、コストは C_i です。
高橋くんは、弱いカードは要らないので捨てることにしました。具体的には、以下の操作をできなくなるまで繰り返します。
- 2 つのカード x, y であって、 A_x > A_y かつ C_x < C_y であるようなものを選ぶ。カード y を捨てる。
操作ができなくなったとき、捨てられなかったカードの集合は一意に定まることが証明できます。これを求めてください。
制約
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i, C_i \leq 10^9
- A_1, A_2, \dots ,A_N は全て異なる
- C_1, C_2, \dots ,C_N は全て異なる
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 C_1 A_2 C_2 \vdots A_N C_N
出力
捨てられなかったカードは m 枚あり、それらの番号が昇順に i_1, i_2, \dots ,i_m であったとする。このとき、以下の形式で出力せよ。
m i_1 i_2 \cdots i_m
入力例 1
3 2 4 1 1 3 2
出力例 1
2 2 3
カード 1, 3 に注目すると、 A_1 < A_3 かつ C_1 > C_3 なのでカード 1 を捨てることができます。
それ以上操作をすることはできません。このときカード 2, 3 が残っているので、これらを出力します。
入力例 2
5 1 1 10 2 100 3 1000 4 10000 5
出力例 2
5 1 2 3 4 5
この場合、どのカードも捨てることができません。
入力例 3
6 32 101 65 78 2 29 46 55 103 130 52 40
出力例 3
4 2 3 5 6
Score : 350 points
Problem Statement
Takahashi has N cards from the card game "AtCoder Magics." The i-th card will be called card i. Each card has two parameters: strength and cost. Card i has a strength of A_i and a cost of C_i.
He does not like weak cards, so he will discard them. Specifically, he will repeat the following operation until it can no longer be performed:
- Choose two cards x and y such that A_x > A_y and C_x < C_y. Discard card y.
It can be proved that the set of remaining cards when the operations can no longer be performed is uniquely determined. Find this set of cards.
Constraints
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i, C_i \leq 10^9
- A_1, A_2, \dots ,A_N are all distinct.
- C_1, C_2, \dots ,C_N are all distinct.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 C_1 A_2 C_2 \vdots A_N C_N
Output
Let there be m remaining cards, cards i_1, i_2, \dots, i_m, in ascending order. Print these in the following format:
m i_1 i_2 \cdots i_m
Sample Input 1
3 2 4 1 1 3 2
Sample Output 1
2 2 3
Focusing on cards 1 and 3, we have A_1 < A_3 and C_1 > C_3, so card 1 can be discarded.
No further operations can be performed. At this point, cards 2 and 3 remain, so print them.
Sample Input 2
5 1 1 10 2 100 3 1000 4 10000 5
Sample Output 2
5 1 2 3 4 5
In this case, no cards can be discarded.
Sample Input 3
6 32 101 65 78 2 29 46 55 103 130 52 40
Sample Output 3
4 2 3 5 6
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : {400} 点
問題文
高橋君は AtCoder Land にある屋外アトラクションに K 回乗ろうとしています。このアトラクションの一回の所要時間は T です。
現在の時刻は 0 です。時刻 0 から N までの降水量が与えられます。時刻 i から時刻 i+1 までの降水量は P_i です (0\leq i\lt N)。アトラクションには時刻 0,1,…,N−T に乗ることができます。時刻 t にアトラクションに乗ると時刻 t+T にアトラクションから降りることができ、アトラクションに乗っている間に P_t+P_{t+1}+\dots+P_{t+T-1} だけ濡れます。
高橋君はアトラクションに乗っている間にできるだけ雨に濡れないようにしたいです。時刻 N までに K 回アトラクションに乗るとき、高橋君が濡れる量の総和の最小値を求めてください。ただし、乗り換えにかかる時間や待ち時間は 0 とし、アトラクションから降りた時刻に新たにアトラクションに乗ることができるものとします。
制約
- 1\leq N\leq 2\times 10^5
- 1\leq K\leq \min(N,100)
- 1\leq T\leq N/K
- 0\leq P_i\leq 10^{9}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N K T
P_0 P_1 \ldots P_{N-1}
出力
答えを出力せよ。
入力例 1
8 3 2 3 5 10 4 1 7 3 9
出力例 1
23
次のようにアトラクションに 3 回乗ることで濡れる量を合計で 23 にすることができ、これが最小です。
- アトラクションに時刻 0 に乗り、時刻 2 に降りる。この間に P_0+P_1=3+5=8 濡れる。
- アトラクションに時刻 3 に乗り、時刻 5 に降りる。この間に P_3+P_4=4+1=5 濡れる。
- アトラクションに時刻 5 に乗り、時刻 7 に降りる。この間に P_5+P_6=7+3=10 濡れる。
入力例 2
5 1 3 1000 1 10000 100 10
出力例 2
10101
入力例 3
15 5 2 401054171 63773035 986525245 157986893 799814573 139201145 649233932 351289844 409065258 406122133 957285954 529460482 21179081 795984182 727882733
出力例 3
3522058414
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
H 行 W 列のマス目があります。 上から i 行目 (1\leq i\leq H)、左から j 列目 (1\leq j\leq W) のマスをマス (i,j) と呼ぶことにします。
マス (i,j)\ (1\leq i\leq H,1\leq j\leq W) には非負整数 A _ {i,j} が書かれています。
このマス目にドミノを 0 個以上置きます。 1 つのドミノは隣り合う 2 つのマス、つまり
- 1\leq i\leq H,1\leq j\lt W に対するマス (i,j) とマス (i,j+1)
- 1\leq i\lt H,1\leq j\leq W に対するマス (i,j) とマス (i+1,j)
のどれかに置くことができます。
ただし、同じマスに対して複数のドミノを置くことはできません。
ドミノの置き方に対して、置き方のスコアをドミノが置かれていないマスに書かれた整数すべてのビットごとの排他的論理和として定めます。
ドミノの置き方のスコアとしてありうる最大値を求めてください。
ビットごとの排他的論理和とは
非負整数 A, B のビットごとの排他的論理和 A \oplus B は、以下のように定義されます。
- A \oplus B を二進表記した際の 2^k (k \geq 0) の位の数は、A, B を二進表記した際の 2^k の位の数のうち一方のみが 1 であれば 1、そうでなければ 0 である。
一般に k 個の非負整数 p_1, p_2, p_3, \dots, p_k のビット単位 \mathrm{XOR} は (\dots ((p_1 \oplus p_2) \oplus p_3) \oplus \dots \oplus p_k) と定義され、これは p_1, p_2, p_3, \dots, p_k の順番によらないことが証明できます。
制約
- 1\leq H
- 1\leq W
- HW\leq20
- 0\leq A _ {i,j}\lt 2 ^ {60}\ (1\leq i\leq H,1\leq j\leq W)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H W
A _ {1,1} A _ {1,2} \ldots A _ {1,W}
A _ {2,1} A _ {2,2} \ldots A _ {2,W}
\vdots
A _ {H,1} A _ {H,2} \ldots A _ {H,W}
出力
答えを出力せよ。
入力例 1
3 4 1 2 3 8 4 0 7 10 5 2 4 2
出力例 1
15
与えられたマス目は以下のようになります。
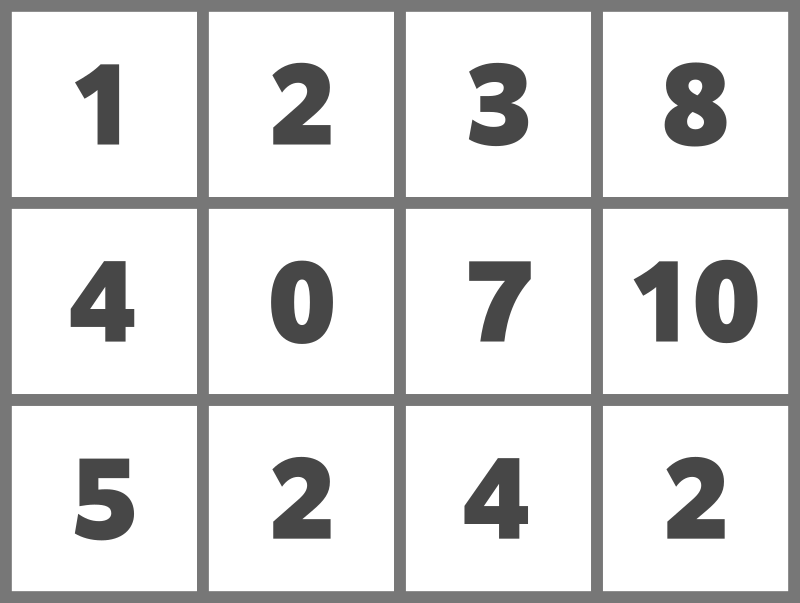
例えば、次のようにドミノを置くことでスコアを 15 とすることができます。
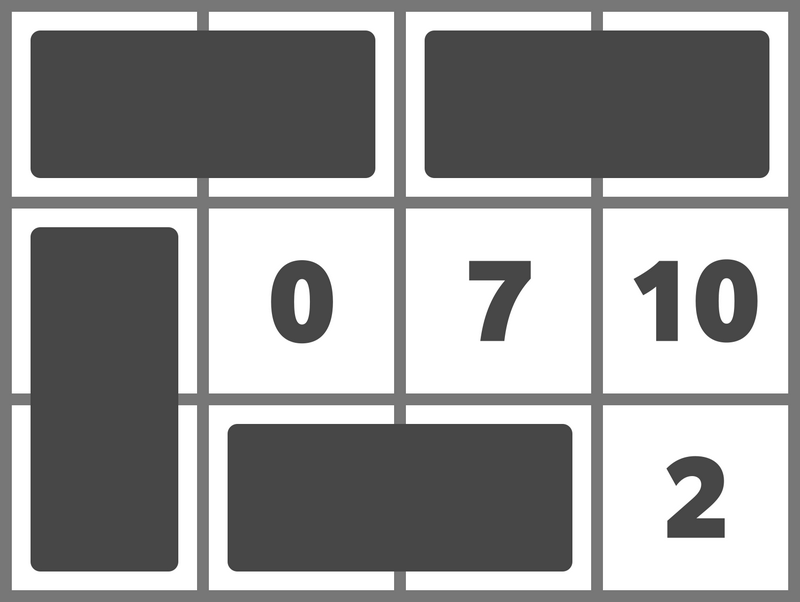
スコアを 16 以上にすることはできないため、15 を出力してください。
入力例 2
1 11 1 2 4 8 16 32 64 128 256 512 1024
出力例 2
2047
ドミノを 1 枚も置かないこともできます。
入力例 3
4 5 74832 16944 58683 32965 97236 52995 43262 51959 40883 58715 13846 24919 65627 11492 63264 29966 98452 75577 40415 77202
出力例 3
131067
Score : 425 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top (1\leq i\leq H) and the j-th column from the left (1\leq j\leq W).
Cell (i,j)\ (1\leq i\leq H,1\leq j\leq W) has a non-negative integer A_{i,j} written on it.
Let us place zero or more dominoes on the grid. A domino covers two adjacent cells, namely one of the following pairs:
- cells (i,j) and (i,j+1) for 1\leq i\leq H,1\leq j\lt W;
- cells (i,j) and (i+1,j) for 1\leq i\lt H,1\leq j\leq W.
No cell may be covered by more than one domino.
For a placement of dominoes, define its score as the bitwise XOR of all integers written in cells not covered by any domino.
Find the maximum possible score.
What is bitwise XOR?
For non-negative integers A and B, their bitwise XOR A \oplus B is defined as follows:
- In binary, the 2^k bit (k \ge 0) of A \oplus B is 1 if exactly one of A and B has 1 in that bit, and 0 otherwise.
For k non-negative integers p_1, p_2, p_3, \dots, p_k, their bitwise XOR is (\dots ((p_1 \oplus p_2) \oplus p_3) \oplus \dots \oplus p_k), which can be proved to be independent of the order of the operands.
Constraints
- 1 \le H
- 1 \le W
- HW \le 20
- 0 \le A_{i,j} < 2^{60} (1 \le i \le H,\ 1 \le j \le W)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H W
A _ {1,1} A _ {1,2} \ldots A _ {1,W}
A _ {2,1} A _ {2,2} \ldots A _ {2,W}
\vdots
A _ {H,1} A _ {H,2} \ldots A _ {H,W}
Output
Output the answer.
Sample Input 1
3 4 1 2 3 8 4 0 7 10 5 2 4 2
Sample Output 1
15
The grid is as follows:

For example, the placement below yields a score of 15.

No placement achieves a score of 16 or higher, so output 15.
Sample Input 2
1 11 1 2 4 8 16 32 64 128 256 512 1024
Sample Output 2
2047
You may also choose to place no dominoes.
Sample Input 3
4 5 74832 16944 58683 32965 97236 52995 43262 51959 40883 58715 13846 24919 65627 11492 63264 29966 98452 75577 40415 77202
Sample Output 3
131067
Time Limit: 4 sec / Memory Limit: 1024 MiB
配点 : 450 点
問題文
N 個の島と、2 つの島の間を双方向に結ぶ M 本の橋があり、
それぞれ島 1, 島 2, \ldots, 島 N および 橋 1, 橋 2, \ldots, 橋 M と番号づけられています。
橋 i は島 U_i と島 V_i を相互に結んでおり、どちらの方向に移動するにも T_i だけ時間がかかります。
ここで、橋の両端が同一の島であるような橋は存在しませんが、ある 2 つの島の間が 2 本以上の橋で直接繋がれている可能性はあります。
また、どの 2 つの島の間もいくつかの橋をわたって移動することができます。
Q 個の問題が与えられるので、各問題に対する答えを求めてください。i 番目の問題は次のようなものです。
相異なる K_i 本の橋、橋 B_{i,1}, 橋 B_{i,2}, \ldots, 橋 B_{i,K_i} が与えられます。
これらの橋をすべて 1 回以上わたり、島 1 から島 N まで移動するために必要な時間の最小値を求めてください。
ただし、島 1 から島 N までの移動において、橋をわたって島の間を移動するのにかかる時間以外は無視できるものとします。
また、与えられた橋はどの順で、またどの向きにわたってもかまいません。
制約
- 2\leq N \leq 400
- N-1\leq M \leq 2\times 10^5
- 1\leq U_i<V_i\leq N
- 1\leq T_i\leq 10^9
- 1\leq Q\leq 3000
- 1\leq K_i\leq 5
- 1\leq B_{i,1}<B_{i,2}<\cdots<B_{i,K_i}\leq M
- 入力はすべて整数
- どの 2 つの島の間もいくつかの橋をわたって移動することができる。
入力
入力は以下の形式で標準入力から与えられる。
N M
U_1 V_1 T_1
U_2 V_2 T_2
\vdots
U_M V_M T_M
Q
K_1
B_{1,1} B_{1,2} \cdots B_{1,{K_1}}
K_2
B_{2,1} B_{2,2} \cdots B_{2,{K_2}}
\vdots
K_Q
B_{Q,1} B_{Q,2} \cdots B_{Q,{K_Q}}
出力
Q 行出力せよ。i 行目(1\leq i\leq Q)には i 番目の問題に対する答えを整数で出力せよ。
入力例 1
3 5 1 2 10 1 3 20 1 3 30 2 3 15 2 3 25 2 1 1 2 3 5
出力例 1
25 70
1 番目の問題では橋 1 をわたった上で島 1 から島 3 へ移動するために必要な時間の最小値を求める必要があります。
橋 1 を使って島 1 から島 2 に移動した後に橋 4 を使って島 2 から島 3 に移動したとき時間は 10+15=25 だけかかり、このときが最小です。
よって、1 行目には 25 を出力します。
2 番目の問題では橋 3 および橋 5 をわたった上で島 1 から島 3 へ移動するために必要な時間の最小値を求める必要があります。
橋 3 を通って島 1 から島 3 に移動した後に橋 5 を使って島 2 へ移動し、橋 4 を使用して島 3 に移動したとき時間は 30+25+15=70 だけかかり、このときが最小です。よって、2 行目には 70 を出力します。
入力例 2
6 6 1 5 1 2 5 1 2 4 1 3 4 1 3 6 1 1 6 1 2 5 1 2 3 4 5 1 5
出力例 2
5 3
各問題において指定された橋をわたる際、わたる方向はどちらでも問題ありません。
入力例 3
5 5 1 2 1000000000 2 3 1000000000 3 4 1000000000 4 5 1000000000 1 5 1000000000 1 1 3
出力例 3
4000000000
答えが 32bit 整数型に収まらない可能性があることに注意してください。
Score : 450 points
Problem Statement
There are N islands and M bidirectional bridges connecting two islands. The islands and bridges are numbered 1, 2, \ldots, N and 1, 2, \ldots, M, respectively.
Bridge i connects islands U_i and V_i, and the time it takes to cross it in either direction is T_i.
No bridge connects an island to itself, but it is possible for two islands to be directly connected by more than one bridge.
One can travel between any two islands using some bridges.
You are given Q queries, so answer each of them. The i-th query is as follows:
You are given K_i distinct bridges: bridges B_{i,1}, B_{i,2}, \ldots, B_{i,K_i}.
Find the minimum time required to travel from island 1 to island N using each of these bridges at least once.
Only consider the time spent crossing bridges.
You can cross the given bridges in any order and in any direction.
Constraints
- 2 \leq N \leq 400
- N-1 \leq M \leq 2 \times 10^5
- 1 \leq U_i < V_i \leq N
- 1 \leq T_i \leq 10^9
- 1 \leq Q \leq 3000
- 1 \leq K_i \leq 5
- 1 \leq B_{i,1} < B_{i,2} < \cdots < B_{i,K_i} \leq M
- All input values are integers.
- It is possible to travel between any two islands using some bridges.
Input
The input is given from Standard Input in the following format:
N M
U_1 V_1 T_1
U_2 V_2 T_2
\vdots
U_M V_M T_M
Q
K_1
B_{1,1} B_{1,2} \cdots B_{1,{K_1}}
K_2
B_{2,1} B_{2,2} \cdots B_{2,{K_2}}
\vdots
K_Q
B_{Q,1} B_{Q,2} \cdots B_{Q,{K_Q}}
Output
Print Q lines. The i-th line (1 \leq i \leq Q) should contain the answer to the i-th query as an integer.
Sample Input 1
3 5 1 2 10 1 3 20 1 3 30 2 3 15 2 3 25 2 1 1 2 3 5
Sample Output 1
25 70
For the first query, we need to find the minimum time to travel from island 1 to island 3 while using bridge 1. The minimum time is achieved by using bridge 1 to move from island 1 to island 2, then using bridge 4 to move from island 2 to island 3. The time taken is 10 + 15 = 25. Hence, print 25 on the first line.
For the second query, we need to find the minimum time to travel from island 1 to island 3 while using both bridges 3 and 5. The minimum time is achieved by using bridge 3 to move from island 1 to island 3, then using bridge 5 to move to island 2, and finally using bridge 4 to return to island 3. The time taken is 30 + 25 + 15 = 70. Hence, print 70 on the second line.
Sample Input 2
6 6 1 5 1 2 5 1 2 4 1 3 4 1 3 6 1 1 6 1 2 5 1 2 3 4 5 1 5
Sample Output 2
5 3
For each query, you can cross the specified bridges in either direction.
Sample Input 3
5 5 1 2 1000000000 2 3 1000000000 3 4 1000000000 4 5 1000000000 1 5 1000000000 1 1 3
Sample Output 3
4000000000
Beware that the answer may not fit in a 32-bit integer.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
高橋君のタンスの中には N 色の靴下があり、色 i の靴下は A_i 枚あります。
高橋君ははじめこれらの靴下とは別に色 C の靴下を 1 枚タンスの外に持っており、操作を終える条件を満たすまで以下の操作を繰り返します。
- タンスから靴下を 1 枚一様ランダムに選んで取り出す。その後、タンスの外に持っている 2 枚の靴下が同じ色ならば操作を終える。そうでないならば、片方の靴下を選んでタンスに戻す。ただし、高橋君は常に今後の靴下を取り出す回数の期待値が最小となるようにタンスに戻す靴下を選ぶ。
操作を終えるまでに靴下を取り出す回数の期待値を \bmod\ 998244353 で求めてください。
期待値を \bmod\ 998244353 で求めるとは
この問題の制約のもとで、期待値は存在し、有理数になることが証明できます。 また、その値を既約分数 \frac{P}{Q} (Q > 0) で表したとき、Q \not\equiv 0 \pmod{998244353} となることも証明できます。 よって、R \times Q \equiv P \pmod{998244353}, 0 \leq R < 998244353 を満たす整数 R が一意に定まります。 期待値を \bmod\ 998244353 で求めるとは、この R の値を求めることを指します。
制約
- 1 \leq N \leq 3 \times 10^5
- 1 \leq C \leq N
- 1 \leq A_i \leq 3000
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N C A_1 A_2 \ldots A_N
出力
答えを出力せよ。
入力例 1
3 2 3 1 2
出力例 1
249561092
靴下を取り出す回数の期待値は \frac{15}{4} となります。
入力例 2
8 4 4 1 6 2 5 1 7 3
出力例 2
393623786
Score : 525 points
Problem Statement
In Takahashi's chest of drawers, there are socks of N colors, with A_i socks of color i.
Initially, Takahashi has one sock of color C outside the chest of drawers, separate from these socks, and repeats the following operation until the termination condition is met:
- Uniformly randomly choose and draw 1 sock from the chest of drawers. Then, if the two socks he has outside the chest of drawers are the same color, terminate the operation. Otherwise, choose one of the socks and put it back in the chest of drawers. He always chooses the sock to put back so as to minimize the expected number of future sock draws.
Find the expected number, modulo 998244353, of sock draws until the operation terminates.
Finding the expected value modulo 998244353
Under the constraints of this problem, it can be proved that the expected value exists and is a rational number. It can also be proved that when this value is expressed as an irreducible fraction \frac{P}{Q} (Q > 0), we have Q \not\equiv 0 \pmod{998244353}. Therefore, there uniquely exists an integer R satisfying R \times Q \equiv P \pmod{998244353}, 0 \leq R < 998244353. Finding the expected value modulo 998244353 means finding this value of R.
Constraints
- 1 \leq N \leq 3 \times 10^5
- 1 \leq C \leq N
- 1 \leq A_i \leq 3000
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N C A_1 A_2 \ldots A_N
Output
Output the answer.
Sample Input 1
3 2 3 1 2
Sample Output 1
249561092
The expected number of sock draws is \frac{15}{4}.
Sample Input 2
8 4 4 1 6 2 5 1 7 3
Sample Output 2
393623786