AtCoder Daily Training ALL 2025/09/02 19:30start

A - Rearranging ABC

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 100 点

問題文

長さ 3 の英大文字からなる文字列 S が与えられます。

S の各文字を並び替えることで S を文字列 ABC と一致させることができるか判定してください。

制約

S は英大文字からなる長さ 3 の文字列

入力

入力は以下の形式で標準入力から与えられる。

出力

S の各文字を並び替えることで文字列 ABC と一致させることができるなら Yes を、そうでないなら No を出力せよ。

入力例 1

BAC

出力例 1

Yes

S の 1 文字目と S の 2 文字目を入れ替えることで ABC と一致させることができます。

入力例 2

AAC

出力例 2

No

どのように並び替えても S を ABC と一致させることはできません。

入力例 3

ABC

出力例 3

Yes

入力例 4

ARC

出力例 4

No

Score : 100 points

Problem Statement

You are given a string S of length 3 consisting of uppercase English letters.

Determine whether it is possible to rearrange the characters in S to make it match the string ABC.

Constraints

S is a string of length 3 consisting of uppercase English letters.

Input

The input is given from Standard Input in the following format:

Output

Print Yes if it is possible to rearrange the characters in S to make it match the string ABC, and No otherwise.

Sample Input 1

BAC

Sample Output 1

Yes

You can make S match ABC by swapping the first and second characters of S.

Sample Input 2

AAC

Sample Output 2

No

You cannot make S match ABC no matter how you rearrange the characters.

Sample Input 3

ABC

Sample Output 3

Yes

Sample Input 4

ARC

Sample Output 4

No

B - Alternately

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 100 点

問題文

N 人が一列に並んでいます。列の状態は長さ N の文字列 S で与えられ、前から i 番目の人は S の i 文字目が M のとき男性、F のとき女性です。

男女が交互に並んでいるかどうか判定してください。

男性同士が隣り合う箇所も女性同士が隣り合う箇所も存在しないとき、かつ、そのときに限り、男女が交互に並んでいるといいます。

制約

1 \leq N \leq 100
N は整数である
S は M および F のみからなる長さ N の文字列である

入力

入力は以下の形式で標準入力から与えられる。

N
S

出力

男女が交互に並んでいるとき Yes、そうでないとき No と出力せよ。

入力例 1

6
MFMFMF

出力例 1

Yes

男性同士が隣り合う箇所も女性同士が隣り合う箇所も存在せず、男女が交互に並んでいます。

入力例 2

9
FMFMMFMFM

出力例 2

No

入力例 3

1
F

出力例 3

Yes

Score : 100 points

Problem Statement

There is a row of N people. They are described by a string S of length N. The i-th person from the front is male if the i-th character of S is M, and female if it is F.

Determine whether the men and women are alternating.

It is said that the men and women are alternating if and only if there is no position where two men or two women are adjacent.

Constraints

1 \leq N \leq 100
N is an integer.
S is a string of length N consisting of M and F.

Input

The input is given from Standard Input in the following format:

N
S

Output

Print Yes if the men and women are alternating, and No otherwise.

Sample Input 1

6
MFMFMF

Sample Output 1

Yes

There is no position where two men or two women are adjacent, so the men and women are alternating.

Sample Input 2

9
FMFMMFMFM

Sample Output 2

No

Sample Input 3

1
F

Sample Output 3

Yes

C - AtCoder Janken 2

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 200 点

問題文

N 人の AtCoder ユーザーが集まり、 AtCoderじゃんけん2 を行います。i 人目のユーザー名は S_i 、レートは C_i です。

AtCoderじゃんけん2 は以下の手順で行われます。

それぞれのユーザーに、ユーザー名の辞書順に 0, 1, \dots ,N - 1 の番号を割り当てる。
N 人のレートの総和を T とする。番号 T \bmod N を割り当てられたユーザーが勝者となる。

勝者のユーザー名を出力してください。

辞書順とは？

辞書順とは簡単に説明すると「単語が辞書に載っている順番」を意味します。より厳密な説明として、英小文字からなる相異なる文字列 S, T の大小を判定するアルゴリズムを以下に説明します。

以下では「 S の i 文字目の文字」を S_i のように表します。また、 S が T より辞書順で小さい場合は S \lt T 、大きい場合は S \gt T と表します。

S, T のうち長さが大きくない方の文字列の長さを L とします。i=1,2,\dots,L に対して S_i と T_i が一致するか調べます。
S_i \neq T_i である i が存在する場合、そのような i のうち最小のものを j とします。そして、S_j と T_j を比較して、S_j が T_j よりアルファベット順で小さい場合は S \lt T 、そうでない場合は S \gt T と決定して、アルゴリズムを終了します。
S_i \neq T_i である i が存在しない場合、S と T の長さを比較して、S が T より短い場合は S \lt T 、長い場合は S \gt T と決定して、アルゴリズムを終了します。

制約

1 \leq N \leq 100
S_i は英小文字からなる長さ 3 以上 16 以下の文字列
S_1, S_2, \dots ,S_N は全て異なる
1 \leq C_i \leq 4229
C_i は整数

入力

入力は以下の形式で標準入力から与えられる。

N
S_1 C_1
S_2 C_2
\vdots
S_N C_N

出力

答えを一行に出力せよ。

入力例 1

3
takahashi 2
aoki 6
snuke 5

出力例 1

snuke

3 人のレートの総和は 13 です。また、それぞれの名前を辞書順に並び替えると、 aoki snuke takahashi の順になるので aoki に番号 0 が、 snuke に番号 1 が、 takahashi に番号 2 が割り当てられます。

13 \bmod 3 = 1 なので、番号 1 を割り当てられた snuke を出力します。

入力例 2

3
takahashi 2813
takahashixx 1086
takahashix 4229

出力例 2

takahashix

Score : 200 points

Problem Statement

N AtCoder users have gathered to play AtCoder RPS 2. The i-th user's name is S_i and their rating is C_i.

AtCoder RPS 2 is played as follows:

Assign the numbers 0, 1, \dots, N - 1 to the users in lexicographical order of their usernames.
Let T be the sum of the ratings of the N users. The user assigned the number T \bmod N is the winner.

Print the winner's username.

What is lexicographical order?

Lexicographical order, simply put, means "the order in which words appear in a dictionary." More precisely, the algorithm to determine the order of two distinct strings S and T consisting of lowercase English letters is as follows:

Here, "the i-th character of S" is denoted as S_i. If S is lexicographically smaller than T, we write S \lt T, and if S is larger, we write S \gt T.

Let L be the length of the shorter string among S and T. Check if S_i and T_i match for i=1,2,\dots,L.
If there exists an i such that S_i \neq T_i, let j be the smallest such i. Compare S_j and T_j. If S_j is alphabetically smaller than T_j, then S \lt T. Otherwise, S \gt T. The algorithm ends here.
If there is no i such that S_i \neq T_i, compare the lengths of S and T. If S is shorter than T, then S \lt T. If S is longer, then S \gt T. The algorithm ends here.

Constraints

1 \leq N \leq 100
S_i is a string consisting of lowercase English letters with length between 3 and 16, inclusive.
S_1, S_2, \dots, S_N are all distinct.
1 \leq C_i \leq 4229
C_i is an integer.

Input

The input is given from Standard Input in the following format:

N
S_1 C_1
S_2 C_2
\vdots
S_N C_N

Output

Print the answer on a single line.

Sample Input 1

3
takahashi 2
aoki 6
snuke 5

Sample Output 1

snuke

The sum of the ratings of the three users is 13. Sorting their names in lexicographical order yields aoki, snuke, takahashi, so aoki is assigned number 0, snuke is 1, and takahashi is 2.

Since 13 \bmod 3 = 1, print snuke, who is assigned number 1.

Sample Input 2

3
takahashi 2813
takahashixx 1086
takahashix 4229

Sample Output 2

takahashix

D - Grid Rotation

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 250 点

問題文

縦 N 行横 N 列からなる 2 つのグリッド S,T があります。グリッドの上から i 行目、左から j 列目のマスをマス (i,j) と表します。

グリッド S,T の各マスは白または黒のいずれかに塗られています。S_{i,j} が . のとき S のマス (i,j) は白く、S_{i,j} が # のとき S のマス (i,j) は黒く塗られています。T についても同様です。

次の 2 種類の操作を好きな順序で好きな回数行うとき、グリッド S をグリッド T と一致させるために必要な操作回数の最小値を求めてください。

グリッド S のマスを 1 つ選び、色を変更する
グリッド S 全体を 90 度右に回転する

制約

1\leq N \leq 100
N は整数
S_{i,j},T_{i,j} は . または #

入力

入力は以下の形式で標準入力から与えられる。

N
S_{1,1}S_{1,2}\dots S_{1,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,N}
\vdots
T_{N,1}T_{N,2}\dots T_{N,N}

出力

答えを出力せよ。

入力例 1

4
###.
..#.
..#.
..#.
...#
...#
###.
....

出力例 1

下図のようにして 2 回の操作で S を T と一致させることができます。

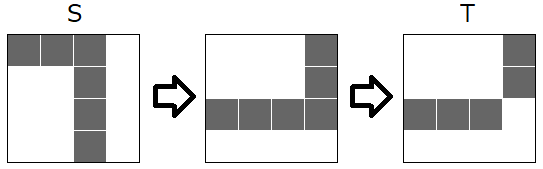
入力例 2

13
.#..###..##..
#.#.#..#.#.#.
#.#.###..#...
###.#..#.#.#.
#.#.###..##..
.............
..#...#....#.
.##..#.#..##.
#.#..#.#.#.#.
####.#.#.####
..#..#.#...#.
..#...#....#.
.............
.............
.#....#...#..
.#...#.#..#..
####.#.#.####
.#.#.###..#.#
.##....#..##.
.#....#...#..
.............
..##..###.#.#
.#.#.#..#.###
.#.#..###.#.#
.#.#.#..#.#.#
..##..###..#.

出力例 2

Score : 250 points

Problem Statement

There are two grids S and T, each with N rows and N columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.

Each cell of grids S and T is colored either white or black. Cell (i,j) of S is white if S_{i,j} is ., and black if S_{i,j} is #. The same applies to T.

You may perform the following two types of operations any number of times in any order. Find the minimum number of operations required to make grid S identical to grid T.

Choose one cell of grid S and change its color.
Rotate the entire grid S 90 degrees clockwise.

Constraints

1 \le N \le 100
N is an integer.
Each of S_{i,j} and T_{i,j} is . or #.

Input

The input is given from Standard Input in the following format:

N
S_{1,1}S_{1,2}\dots S_{1,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,N}
\vdots
T_{N,1}T_{N,2}\dots T_{N,N}

Output

Output the minimum number of operations required.

Sample Input 1

4
###.
..#.
..#.
..#.
...#
...#
###.
....

Sample Output 1

You can match S to T in two operations as shown below.

Sample Input 2

13
.#..###..##..
#.#.#..#.#.#.
#.#.###..#...
###.#..#.#.#.
#.#.###..##..
.............
..#...#....#.
.##..#.#..##.
#.#..#.#.#.#.
####.#.#.####
..#..#.#...#.
..#...#....#.
.............
.............
.#....#...#..
.#...#.#..#..
####.#.#.####
.#.#.###..#.#
.##....#..##.
.#....#...#..
.............
..##..###.#.#
.#.#.#..#.###
.#.#..###.#.#
.#.#.#..#.#.#
..##..###..#.

Sample Output 2

E - Triple Attack

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 300 点

問題文

あなたはゲームをプレイしています。

N 人の敵が一列に並んでおり、前から i 番目の敵の体力は H_i です。

あなたは 0 で初期化された変数 T を使い、全ての敵の体力が 0 以下になるまで次の行動を繰り返します。

T を 1 増やす。その後、体力が 1 以上である最も前の敵を攻撃する。このとき、T が 3 の倍数ならばその敵の体力は 3 減り、そうでないなら 1 減る。

全ての敵の体力が 0 以下になったときの T の値を求めてください。

制約

1 \leq N \leq 2\times 10^5
1 \leq H_i \leq 10^9
入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N
H_1 H_2 \ldots H_N

出力

答えを出力せよ。

入力例 1

3
6 2 2

出力例 1

行動は次のように行われます。

T=1 になる。1 番目の敵を攻撃し、その敵の体力は 6-1=5 となる。
T=2 になる。1 番目の敵を攻撃し、その敵の体力は 5-1=4 となる。
T=3 になる。1 番目の敵を攻撃し、その敵の体力は 4-3=1 となる。
T=4 になる。1 番目の敵を攻撃し、その敵の体力は 1-1=0 となる。
T=5 になる。2 番目の敵を攻撃し、その敵の体力は 2-1=1 となる。
T=6 になる。2 番目の敵を攻撃し、その敵の体力は 1-3=-2 となる。
T=7 になる。3 番目の敵を攻撃し、その敵の体力は 2-1=1 となる。
T=8 になる。3 番目の敵を攻撃し、その敵の体力は 1-1=0 となる。

入力例 2

9
1 12 123 1234 12345 123456 1234567 12345678 123456789

出力例 2

82304529

入力例 3

5
1000000000 1000000000 1000000000 1000000000 1000000000

出力例 3

3000000000

オーバーフローに注意してください。

Score : 300 points

Problem Statement

You are playing a game.

There are N enemies lined up in a row, and the i-th enemy from the front has a health of H_i.

You will repeat the following action until the healths of all enemies become 0 or less, using a variable T initialized to 0.

Increase T by 1. Then, attack the frontmost enemy with health 1 or more. If T is a multiple of 3, the enemy's health decreases by 3; otherwise, it decreases by 1.

Find the value of T when the healths of all enemies become 0 or less.

Constraints

1 \leq N \leq 2\times 10^5
1 \leq H_i \leq 10^9
All input values are integers.

Input

The input is given from Standard Input in the following format:

N
H_1 H_2 \ldots H_N

Output

Print the answer.

Sample Input 1

3
6 2 2

Sample Output 1

The actions are performed as follows:

T becomes 1. Attack the 1st enemy, and its health becomes 6-1=5.
T becomes 2. Attack the 1st enemy, and its health becomes 5-1=4.
T becomes 3. Attack the 1st enemy, and its health becomes 4-3=1.
T becomes 4. Attack the 1st enemy, and its health becomes 1-1=0.
T becomes 5. Attack the 2nd enemy, and its health becomes 2-1=1.
T becomes 6. Attack the 2nd enemy, and its health becomes 1-3=-2.
T becomes 7. Attack the 3rd enemy, and its health becomes 2-1=1.
T becomes 8. Attack the 3rd enemy, and its health becomes 1-1=0.

Sample Input 2

9
1 12 123 1234 12345 123456 1234567 12345678 123456789

Sample Output 2

82304529

Sample Input 3

5
1000000000 1000000000 1000000000 1000000000 1000000000

Sample Output 3

3000000000

Beware of integer overflow.

F - Ameba

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 300 点

問題文

あなたはアメーバの観察記録をつけました。

最初 1 匹のアメーバがおり、番号は 1 です。

観察記録は時系列順に N 個あり、i 番目の観察記録は「番号 A_i のアメーバが分裂して消滅し、新たに 2 匹のアメーバが生まれ、それらにそれぞれ 2i,2i+1 と番号をつけた」というものです。
このとき、アメーバ A_i をアメーバ 2i,2i+1 の親と呼びます。

各 k=1,\ldots,2N+1 について、アメーバ k から何代親を遡るとアメーバ 1 になるか求めてください。

制約

1 \leq N \leq 2\times 10^5
観察記録は矛盾していない。すなわち
- 1\leq A_i \leq 2i-1
- A_i は相異なる整数

入力

入力は以下の形式で標準入力から与えられる。

N
A_1 A_2 \ldots A_N

出力

2N+1 行出力せよ。k 行目にはアメーバ k から何代親を遡るとアメーバ 1 になるかを出力せよ。

入力例 1

2
1 2

出力例 1

アメーバ 1 からアメーバ 2,3 が生まれ、アメーバ 2 からアメーバ 4,5 が生まれました。

アメーバ 1 は 0 代遡るとアメーバ 1 になります。
アメーバ 2 は 1 代遡るとアメーバ 1 になります。
アメーバ 3 は 1 代遡るとアメーバ 1 になります。
アメーバ 4 は 1 代遡るとアメーバ 2 になり、2 代遡るとアメーバ 1 になります。
アメーバ 5 は 1 代遡るとアメーバ 2 になり、2 代遡るとアメーバ 1 になります。

入力例 2

4
1 3 5 2

出力例 2

Score : 300 points

Problem Statement

You observed amoebae and kept some records.

Initially, there was one amoeba, numbered 1.

You made N records. According to the i-th record, the amoeba numbered A_i disappeared by dividing itself into two new amoebae, which were then numbered 2i and 2i+1.
Here, amoeba A_i is said to be the parent of amoebae 2i and 2i+1.

For each k=1,\ldots,2N+1, how many generations away is amoeba k from amoeba 1?

Constraints

1 \leq N \leq 2\times 10^5
The records are consistent. That is:
- 1\leq A_i \leq 2i-1.
- A_i are distinct integers.

Input

The input is given from Standard Input in the following format:

N
A_1 A_2 \ldots A_N

Output

Print 2N+1 lines. The k-th line should contain the generation distance between amoeba 1 and amoeba k.

Sample Input 1

2
1 2

Sample Output 1

From amoeba 1, amoebae 2 and 3 were born. From amoeba 2, amoebae 4 and 5 were born.

Amoeba 1 is zero generations away from amoeba 1.
Amoeba 2 is one generation away from amoeba 1.
Amoeba 3 is one generation away from amoeba 1.
Amoeba 4 is one generation away from amoeba 2, and two generations away from amoeba 1.
Amoeba 5 is one generation away from amoeba 2, and two generations away from amoeba 1.

Sample Input 2

4
1 3 5 2

Sample Output 2

G - At Most 3 (Contestant ver.)

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 400 点

問題文

整数 W が与えられます。
あなたは以下の条件をすべて満たすようにいくつかのおもりを用意することにしました。

おもりの個数は 1 個以上 300 個以下である。
おもりの重さは 10^6 以下の正整数である。
1 以上 W 以下のすべての正整数は 良い整数 である。ここで、以下の条件を満たす正整数 n を良い整数と呼ぶ。
- 用意したおもりのうち \bf{3} 個以下 の異なるおもりを自由に選んで、選んだおもりの重さの和を n にすることができる。

条件を満たすようなおもりの組を 1 つ出力してください。

制約

1 \leq W \leq 10^6
W は整数

入力

入力は以下の形式で標準入力から与えられる。

出力

N をおもりの個数、A_i を i 番目のおもりの重さとして、以下の形式で出力せよ。答えが複数存在する場合、どれを出力しても正解とみなされる。

N
A_1 A_2 \dots A_N

ただし、N および A_1,A_2,\dots,A_N は以下の条件を満たす必要がある。

1 \leq N \leq 300
1 \leq A_i \leq 10^6

入力例 1

出力例 1

3
1 2 3

上の出力は重さ 1 のおもり、重さ 2 のおもり、重さ 3 のおもりの 3 個のおもりを用意しています。
この出力は条件を満たしています。特に 3 番目の条件について、以下のようにおもりを選ぶことで 1 以上 W 以下の整数すべてが良い整数であることが確認できます。

1 番目のおもりのみを選ぶと、重さの和は 1 になる。
2 番目のおもりのみを選ぶと、重さの和は 2 になる。
3 番目のおもりのみを選ぶと、重さの和は 3 になる。
1 番目と 3 番目のおもりを選ぶと、重さの和は 4 になる。
2 番目と 3 番目のおもりを選ぶと、重さの和は 5 になる。
1 番目、2 番目と 3 番目のおもりを選ぶと、重さの和は 6 になる。

入力例 2

出力例 2

6
2 5 1 2 5 1

同じ重さのおもりを 2 個以上用意しても良いです。

Score : 400 points

Problem Statement

You are given an integer W.
You are going to prepare some weights so that all of the conditions below are satisfied.

The number of weights is between 1 and 300, inclusive.
Each weight has a mass of positive integer not exceeding 10^6.
Every integer between 1 and W, inclusive, is a good integer. Here, a positive integer n is said to be a good integer if the following condition is satisfied:
- We can choose at most 3 different weights from the prepared weights with a total mass of n.

Print a combination of weights that satisfies the conditions.

Constraints

1 \leq W \leq 10^6
W is an integer.

Input

Input is given from Standard Input in the following format:

Output

Print in the following format, where N is the number of weights and A_i is the mass of the i-th weight. If multiple solutions exist, printing any of them is accepted.

N
A_1 A_2 \dots A_N

Here, N and A_1,A_2,\dots,A_N should satisfy the following conditions:

1 \leq N \leq 300
1 \leq A_i \leq 10^6

Sample Input 1

Sample Output 1

3
1 2 3

In the output above, 3 weights with masses 1, 2, and 3 are prepared.
This output satisfies the conditions. Especially, regarding the 3-rd condition, we can confirm that every integer between 1 and W, inclusive, is a good integer.

If we choose only the 1-st weight, it has a total mass of 1.
If we choose only the 2-nd weight, it has a total mass of 2.
If we choose only the 3-rd weight, it has a total mass of 3.
If we choose the 1-st and the 3-rd weights, they have a total mass of 4.
If we choose the 2-nd and the 3-rd weights, they have a total mass of 5.
If we choose the 1-st, the 2-nd, and the 3-rd weights, they have a total mass of 6.

Sample Input 2

Sample Output 2

6
2 5 1 2 5 1

You may prepare multiple weights with the same mass.

H - Chinese Restaurant (Three-Star Version)

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 500 点

問題文

回転テーブルの周りに人 0、人 1、\ldots、人 N-1 がこの順番で反時計回りに等間隔で並んでいます。また、人 i の目の前には料理 p_i が置かれています。
あなたは次の操作を 0 回以上何度でも行うことが出来ます。

回転テーブルを反時計回りに 1 周の \frac{1}{N} だけ回す。これによって、(この操作の直前に)人 i の目の前にあった料理は人 (i+1) \bmod N の目の前に移動する。

操作を完了させた後において、人 i の不満度は料理 i が人 (i-k) \bmod N、人 (i+k) \bmod N のいずれかの目の前に置かれているような最小の非負整数 k です。
N 人の不満度の総和の最小値を求めてください。

a \bmod m とは

整数 a と正整数 m に対し、a \bmod m は a-x が m の倍数となるような 0 以上 m 未満の整数 x を表します。(このような x は一意に定まることが証明できます)

制約

3 \leq N \leq 2 \times 10^5
0 \leq p_i \leq N-1
i \neq j ならば p_i \neq p_j
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられる。

N
p_0 \ldots p_{N-1}

出力

答えを出力せよ。

入力例 1

4
1 2 0 3

出力例 1

操作を 1 回行うと下の画像のようになります。

この時、不満度の総和が 2 になることを以下のように確かめられます。

人 0 の不満度は、料理 0 が人 3\ (=(0-1) \bmod 4) の目の前に置かれているので 1 です。
人 1 の不満度は、料理 1 が人 1\ (=(1+0) \bmod 4) の目の前に置かれているので 0 です。
人 2 の不満度は、料理 2 が人 2\ (=(2+0) \bmod 4) の目の前に置かれているので 0 です。
人 3 の不満度は、料理 3 が人 0\ (=(3+1) \bmod 4) の目の前に置かれているので 1 です。

不満度の総和を 2 より小さくすることは出来ないため、答えは 2 です。

入力例 2

3
0 1 2

出力例 2

入力例 3

10
3 9 6 1 7 2 8 0 5 4

出力例 3

Score : 500 points

Problem Statement

Person 0, Person 1, \ldots, and Person (N-1) are sitting around a turntable in counterclockwise order, evenly spaced. Dish p_i is in front of Person i on the table.
You may perform the following operation 0 or more times:

Rotate the turntable by one N-th of a counterclockwise turn. The dish that was in front of Person i right before the rotation is now in front of Person (i+1) \bmod N.

When you are finished, Person i gains frustration of k, where k is the minimum integer such that Dish i is in front of either Person (i-k) \bmod N or Person (i+k) \bmod N.
Find the minimum possible sum of frustration of the N people.

What is a \bmod m?

For an integer a and a positive integer m, a \bmod m denotes the integer x between 0 and (m-1) (inclusive) such that (a-x) is a multiple of m. (It can be proved that such x is unique.)

Constraints

3 \leq N \leq 2 \times 10^5
0 \leq p_i \leq N-1
p_i \neq p_j if i \neq j.
All values in input are integers.

Input

Input is given from Standard Input in the following format:

N
p_0 \ldots p_{N-1}

Output

Print the answer.

Sample Input 1

4
1 2 0 3

Sample Output 1

The figure below shows the table after one operation.

Here, the sum of their frustration is 2 because:

Person 0 gains a frustration of 1 since Dish 0 is in front of Person 3\ (=(0-1) \bmod 4);
Person 1 gains a frustration of 0 since Dish 1 is in front of Person 1\ (=(1+0) \bmod 4);
Person 2 gains a frustration of 0 since Dish 2 is in front of Person 2\ (=(2+0) \bmod 4);
Person 3 gains a frustration of 1 since Dish 3 is in front of Person 0\ (=(3+1) \bmod 4).

We cannot make the sum of their frustration less than 2, so the answer is 2.

Sample Input 2

3
0 1 2

Sample Output 2

Sample Input 3

10
3 9 6 1 7 2 8 0 5 4

Sample Output 3

I - Two Sequence Queries

実行時間制限: 5 sec / メモリ制限: 1024 MiB

配点 : 550 点

問題文

長さ N の数列 A=(A_1,A_2,\ldots,A_N), B=(B_1,B_2,\ldots,B_N) が与えられます。
Q 個のクエリが与えられるので、順に処理してください。

クエリは次の 3 種類です。

1 l r x : A_l, A_{l+1}, \ldots, A_r に x を加える。
2 l r x : B_l, B_{l+1}, \ldots, B_r に x を加える。
3 l r : \displaystyle\sum_{i=l}^r (A_i\times B_i) を 998244353 で割った余りを出力する。

制約

1\leq N,Q\leq 2\times 10^5
0\leq A_i,B_i\leq 10^9
1\leq l\leq r\leq N
1\leq x\leq 10^9
入力はすべて整数
3 種類目のクエリが 1 つ以上存在する。

入力

入力は以下の形式で標準入力から与えられる。ここで、\mathrm{query}_i (1\leq i\leq Q) は i 番目に処理するクエリである。

N Q
A_1 A_2 \ldots A_N
B_1 B_2 \ldots B_N
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q

各クエリは以下のいずれかの形式で与えられる。

1 l r x

2 l r x

3 l r

出力

3 種類目のクエリが K 個あるとき、K 行出力せよ。
i 行目 (1\leq i\leq K) には、i 個目の 3 種類目のクエリに対する出力を出力せよ。

入力例 1

出力例 1

16
25
84

最初、A=(1,3,5,6,8), B=(3,1,2,1,2) です。クエリは次の順で処理されます。

1 個目のクエリでは (1\times 3)+(3\times 1)+(5\times 2)=16 を 998244353 で割った余りである 16 を出力します。
2 個目のクエリでは A_2,A_3,A_4,A_5 に 3 を加えます。A=(1,6,8,9,11) となります。
3 個目のクエリでは (1\times 3)+(6\times 1)+(8\times 2)=25 を 998244353 で割った余りである 25 を出力します。
4 個目のクエリでは A_1,A_2,A_3 に 1 を加えます。A=(2,7,9,9,11) となります。
5 個目のクエリでは B_5 に 2 を加えます。B=(3,1,2,1,4) となります。
6 個目のクエリでは (2\times 3)+(7\times 1)+(9\times 2)+(9\times 1)+(11\times 4)=84 を 998244353 で割った余りである 84 を出力します。

よって、1, 2, 3 行目にはそれぞれ 16, 25, 84 を出力します。

入力例 2

2 3
1000000000 1000000000
1000000000 1000000000
3 1 1
1 2 2 1000000000
3 1 2

出力例 2

716070898
151723988

3 種類目のクエリでは 998244353 で割った余りを出力することに注意してください。

Score : 550 points

Problem Statement

You are given sequences of length N, A=(A_1,A_2,\ldots,A_N) and B=(B_1,B_2,\ldots,B_N).
You are also given Q queries to process in order.

There are three types of queries:

1 l r x : Add x to each of A_l, A_{l+1}, \ldots, A_r.
2 l r x : Add x to each of B_l, B_{l+1}, \ldots, B_r.
3 l r : Print the remainder of \displaystyle\sum_{i=l}^r (A_i\times B_i) when divided by 998244353.

Constraints

1\leq N,Q\leq 2\times 10^5
0\leq A_i,B_i\leq 10^9
1\leq l\leq r\leq N
1\leq x\leq 10^9
All input values are integers.
There is at least one query of the third type.

Input

The input is given from Standard Input in the following format. Here, \mathrm{query}_i (1\leq i\leq Q) is the i-th query to be processed.

N Q
A_1 A_2 \ldots A_N
B_1 B_2 \ldots B_N
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q

Each query is given in one of the following formats:

1 l r x

2 l r x

3 l r

Output

If there are K queries of the third type, print K lines.
The i-th line (1\leq i\leq K) should contain the output for the i-th query of the third type.

Sample Input 1

Sample Output 1

16
25
84

Initially, A=(1,3,5,6,8) and B=(3,1,2,1,2). The queries are processed in the following order:

For the first query, print (1\times 3)+(3\times 1)+(5\times 2)=16 modulo 998244353, which is 16.
For the second query, add 3 to A_2,A_3,A_4,A_5. Now A=(1,6,8,9,11).
For the third query, print (1\times 3)+(6\times 1)+(8\times 2)=25 modulo 998244353, which is 25.
For the fourth query, add 1 to A_1,A_2,A_3. Now A=(2,7,9,9,11).
For the fifth query, add 2 to B_5. Now B=(3,1,2,1,4).
For the sixth query, print (2\times 3)+(7\times 1)+(9\times 2)+(9\times 1)+(11\times 4)=84 modulo 998244353, which is 84.

Thus, the first, second, and third lines should contain 16, 25, and 84, respectively.

Sample Input 2

2 3
1000000000 1000000000
1000000000 1000000000
3 1 1
1 2 2 1000000000
3 1 2

Sample Output 2

716070898
151723988

Make sure to print the sum modulo 998244353 for the third type of query.