Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
ある日、学校へ行くのに疲れてしまった高橋くんは、土曜日まであと何日あるかを知りたくなりました。
その日は平日で、曜日を英語で表すと S だったことが分かっています。その日より後の直近の土曜日は何日後かを求めてください。
なお、月曜日、火曜日、水曜日、木曜日、金曜日はそれぞれ英語で Monday, Tuesday, Wednesday, Thursday, Friday です。
制約
- S は
Monday,Tuesday,Wednesday,Thursday,Fridayのいずれかである
入力
入力は以下の形式で標準入力から与えられる。
S
出力
答えを整数として出力せよ。
入力例 1
Wednesday
出力例 1
3
この日は水曜日なので、3 日後に土曜日になります。
入力例 2
Monday
出力例 2
5
Score : 100 points
Problem Statement
One day, tired from going to school, Takahashi wanted to know how many days there were until Saturday.
We know that the day was a weekday, and the name of the day of the week was S in English.
How many days were there until the first Saturday after that day (including Saturday but not the starting day)?
Constraints
- S is
Monday,Tuesday,Wednesday,Thursday, orFriday.
Input
Input is given from Standard Input in the following format:
S
Output
Print the answer as an integer.
Sample Input 1
Wednesday
Sample Output 1
3
It was Wednesday, so there were 3 days until the first Saturday after that day.
Sample Input 2
Monday
Sample Output 2
5
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
与えられる 5 つの整数 A, B, C, D, E の中に何種類の整数があるかを出力してください。
制約
- 0 \leq A, B, C, D, E \leq 100
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
A B C D E
出力
答えを出力せよ。
入力例 1
31 9 24 31 24
出力例 1
3
与えられる 5 つの整数 31, 9, 24, 31, 24 の中には、9, 24, 31 という 3 種類の整数があります。 よって、3 を出力します。
入力例 2
0 0 0 0 0
出力例 2
1
Score : 100 points
Problem Statement
Print how many distinct integers there are in given five integers A, B, C, D, and E.
Constraints
- 0 \leq A, B, C, D, E \leq 100
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
A B C D E
Output
Print the answer.
Sample Input 1
31 9 24 31 24
Sample Output 1
3
In the given five integers 31, 9, 24, 31, and 24, there are three distinct integers 9, 24, and 31. Thus, 3 should be printed.
Sample Input 2
0 0 0 0 0
Sample Output 2
1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 250 点
問題文
縦 N 行 横 N 列からなる 2 つのグリッド S,T があります。グリッドの上から i 行目、左から j 列目のマスをマス (i,j) と表します。
グリッド S,T の各マスは白または黒のいずれかに塗られています。S_{i,j} が . のとき S のマス (i,j) は白く、S_{i,j} が # のとき S のマス (i,j) は黒く塗られています。T についても同様です。
次の 2 種類の操作を好きな順序で好きな回数行うとき、グリッド S をグリッド T と一致させるために必要な操作回数の最小値を求めてください。
- グリッド S のマスを 1 つ選び、色を変更する
- グリッド S 全体を 90 度右に回転する
制約
- 1\leq N \leq 100
- N は整数
- S_{i,j},T_{i,j} は
.または#
入力
入力は以下の形式で標準入力から与えられる。
N
S_{1,1}S_{1,2}\dots S_{1,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,N}
\vdots
T_{N,1}T_{N,2}\dots T_{N,N}
出力
答えを出力せよ。
入力例 1
4 ###. ..#. ..#. ..#. ...# ...# ###. ....
出力例 1
2
下図のようにして 2 回の操作で S を T と一致させることができます。
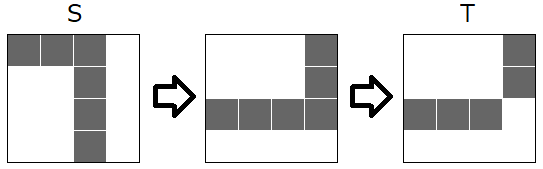
入力例 2
13 .#..###..##.. #.#.#..#.#.#. #.#.###..#... ###.#..#.#.#. #.#.###..##.. ............. ..#...#....#. .##..#.#..##. #.#..#.#.#.#. ####.#.#.#### ..#..#.#...#. ..#...#....#. ............. ............. .#....#...#.. .#...#.#..#.. ####.#.#.#### .#.#.###..#.# .##....#..##. .#....#...#.. ............. ..##..###.#.# .#.#.#..#.### .#.#..###.#.# .#.#.#..#.#.# ..##..###..#.
出力例 2
5
Score : 250 points
Problem Statement
There are two grids S and T, each with N rows and N columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
Each cell of grids S and T is colored either white or black. Cell (i,j) of S is white if S_{i,j} is ., and black if S_{i,j} is #. The same applies to T.
You may perform the following two types of operations any number of times in any order. Find the minimum number of operations required to make grid S identical to grid T.
- Choose one cell of grid S and change its color.
- Rotate the entire grid S 90 degrees clockwise.
Constraints
- 1 \le N \le 100
- N is an integer.
- Each of S_{i,j} and T_{i,j} is
.or#.
Input
The input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}\dots S_{1,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,N}
\vdots
T_{N,1}T_{N,2}\dots T_{N,N}
Output
Output the minimum number of operations required.
Sample Input 1
4 ###. ..#. ..#. ..#. ...# ...# ###. ....
Sample Output 1
2
You can match S to T in two operations as shown below.

Sample Input 2
13 .#..###..##.. #.#.#..#.#.#. #.#.###..#... ###.#..#.#.#. #.#.###..##.. ............. ..#...#....#. .##..#.#..##. #.#..#.#.#.#. ####.#.#.#### ..#..#.#...#. ..#...#....#. ............. ............. .#....#...#.. .#...#.#..#.. ####.#.#.#### .#.#.###..#.# .##....#..##. .#....#...#.. ............. ..##..###.#.# .#.#.#..#.### .#.#..###.#.# .#.#.#..#.#.# ..##..###..#.
Sample Output 2
5
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
正整数 M が与えられます。 以下の条件を全て満たす正整数 N と非負整数列 A=(A_1,A_2,\ldots,A_N) を一つ求めてください。
- 1\le N\le 20
- 0\le A_i\le 10 (1\le i\le N)
- \displaystyle \sum_{i=1}^N 3^{A_i}=M
ただし、制約下では条件を満たす N と A の組が必ず存在することが証明できます。
制約
- 1\le M\le 10^5
入力
入力は以下の形式で標準入力から与えられる。
M
出力
以下の形式で条件を満たす N と A を出力せよ。
N A_1 A_2 \ldots A_N
なお、条件を満たす N と A の組が複数存在する場合は、どれを出力しても正答となる。
入力例 1
6
出力例 1
2 1 1
N=2 、A=(1,1) とすると \displaystyle \sum_{i=1}^N 3^{A_i}=3+3=6 より全ての条件を満たします。
他に N=4 、 A=(0,0,1,0) なども条件を満たします。
入力例 2
100
出力例 2
4 2 0 2 4
入力例 3
59048
出力例 3
20 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
1\le N\le 20 という制約に注意してください。
Score : 200 points
Problem Statement
You are given a positive integer M. Find a positive integer N and a sequence of non-negative integers A = (A_1, A_2, \ldots, A_N) that satisfy all of the following conditions:
- 1 \le N \le 20
- 0 \le A_i \le 10 (1 \le i \le N)
- \displaystyle \sum_{i=1}^N 3^{A_i} = M
It can be proved that under the constraints, there always exists at least one such pair of N and A satisfying the conditions.
Constraints
- 1 \le M \le 10^5
Input
The input is given from Standard Input in the following format:
M
Output
Print N and A satisfying the conditions in the following format:
N A_1 A_2 \ldots A_N
If there are multiple valid pairs of N and A, any of them is acceptable.
Sample Input 1
6
Sample Output 1
2 1 1
For example, with N=2 and A=(1,1), we have \displaystyle \sum_{i=1}^N 3^{A_i} = 3+3=6, satisfying all conditions.
Another example is N=4 and A=(0,0,1,0), which also satisfies the conditions.
Sample Input 2
100
Sample Output 2
4 2 0 2 4
Sample Input 3
59048
Sample Output 3
20 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
Note the condition 1 \le N \le 20.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
座標平面上に 2\times1 の大きさのタイルが敷き詰められています。 タイルは、次の規則に従って敷き詰められています。
- 整数の組 (i,j) に対し、正方形 A _ {i,j}=\lbrace(x,y)\mid i\leq x\leq i+1\wedge j\leq y\leq j+1\rbrace は 1 つのタイルに含まれる。
- i+j が偶数のとき、A _ {i,j} と A _ {i + 1,j} は同じタイルに含まれる。
ただし、タイルは境界を含むものとし、共通部分が正の面積をもつような 2 つの異なるタイルは存在しないとします。
原点の近くでは、タイルは以下のように敷き詰められています。

高橋君は、はじめ座標平面上の点 (S _ x+0.5,S _ y+0.5) にいます。
高橋君は、次の移動を好きなだけ繰り返します。
- 上下左右の方向と正の整数 n を選ぶ。その方向に n だけ進む。
高橋君が異なるタイルを通るたび、高橋君は通行料を 1 だけ支払います。
高橋君が点 (T _ x+0.5,T _ y+0.5) にたどり着くために支払わなければならない通行料の最小値を求めてください。
制約
- 0\leq S _ x\leq2\times10 ^ {16}
- 0\leq S _ y\leq2\times10 ^ {16}
- 0\leq T _ x\leq2\times10 ^ {16}
- 0\leq T _ y\leq2\times10 ^ {16}
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
S _ x S _ y T _ x T _ y
出力
高橋君が支払わなければならない通行料の最小値を出力せよ。
入力例 1
5 0 2 5
出力例 1
5
例えば、以下のように移動することで支払う通行料を 5 にすることができます。

- 左に 1 進む。通行料を 0 支払う。
- 上に 1 進む。通行料を 1 支払う。
- 左に 1 進む。通行料を 0 支払う。
- 上に 3 進む。通行料を 3 支払う。
- 左に 1 進む。通行料を 0 支払う。
- 上に 1 進む。通行料を 1 支払う。
支払う通行料を 4 以下にすることはできないので、5 を出力してください。
入力例 2
3 1 4 1
出力例 2
0
通行料を支払わなくてよい場合もあります。
入力例 3
2552608206527595 5411232866732612 771856005518028 7206210729152763
出力例 3
1794977862420151
出力すべき値が 32\operatorname{bit} 整数の範囲に収まらない場合があることに注意してください。
Score : 350 points
Problem Statement
The coordinate plane is covered with 2\times1 tiles. The tiles are laid out according to the following rules:
- For an integer pair (i,j), the square A _ {i,j}=\lbrace(x,y)\mid i\leq x\leq i+1\wedge j\leq y\leq j+1\rbrace is contained in one tile.
- When i+j is even, A _ {i,j} and A _ {i + 1,j} are contained in the same tile.
Tiles include their boundaries, and no two different tiles share a positive area.
Near the origin, the tiles are laid out as follows:

Takahashi starts at the point (S _ x+0.5,S _ y+0.5) on the coordinate plane.
He can repeat the following move as many times as he likes:
- Choose a direction (up, down, left, or right) and a positive integer n. Move n units in that direction.
Each time he enters a tile, he pays a toll of 1.
Find the minimum toll he must pay to reach the point (T _ x+0.5,T _ y+0.5).
Constraints
- 0\leq S _ x\leq2\times10 ^ {16}
- 0\leq S _ y\leq2\times10 ^ {16}
- 0\leq T _ x\leq2\times10 ^ {16}
- 0\leq T _ y\leq2\times10 ^ {16}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
S _ x S _ y T _ x T _ y
Output
Print the minimum toll Takahashi must pay.
Sample Input 1
5 0 2 5
Sample Output 1
5
For example, Takahashi can pay a toll of 5 by moving as follows:

- Move left by 1. Pay a toll of 0.
- Move up by 1. Pay a toll of 1.
- Move left by 1. Pay a toll of 0.
- Move up by 3. Pay a toll of 3.
- Move left by 1. Pay a toll of 0.
- Move up by 1. Pay a toll of 1.
It is impossible to reduce the toll to 4 or less, so print 5.
Sample Input 2
3 1 4 1
Sample Output 2
0
There are cases where no toll needs to be paid.
Sample Input 3
2552608206527595 5411232866732612 771856005518028 7206210729152763
Sample Output 3
1794977862420151
Note that the value to be output may exceed the range of a 32-bit integer.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
高橋君は N 日間の鉄道旅行を計画しています。
高橋君はそれぞれの日について、運賃の通常料金を払うか、1 日周遊パスを 1 枚使用するか選ぶことができます。
ここで、1\leq i\leq N について、i 日目の旅行にかかる運賃の通常料金は F_i 円です。
一方、1 日周遊パスは D 枚セットで P 円で発売されており、何セットでも購入することが可能ですが、D 枚単位でしか購入することができません。
また、購入したパスは 1 枚ずつ好きな日に使うことができ、旅行が終了した時点で余っていても構いません。
N 日間の旅行でかかる金額、すなわち 1 日周遊パスの購入にかかった代金と、1 日周遊パスを利用しなかった日における運賃の通常料金の合計金額の和としてあり得る最小値を求めてください。
制約
- 1\leq N\leq 2\times 10^5
- 1\leq D\leq 2\times 10^5
- 1\leq P\leq 10^9
- 1\leq F_i\leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N D P F_1 F_2 \ldots F_N
出力
N 日間の旅行でかかる金額としてあり得る最小値を出力せよ。
入力例 1
5 2 10 7 1 6 3 6
出力例 1
20
1 日周遊パスを 1 セットだけ購入し、1 日目と 3 日目に使用すると、合計金額は (10\times 1)+(0+1+0+3+6)=20 となり、このときかかる金額が最小となります。
よって、20 を出力します。
入力例 2
3 1 10 1 2 3
出力例 2
6
3 日間すべてにおいて運賃の通常料金を支払ったときに最小となります。
入力例 3
8 3 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
出力例 3
3000000000
1 日周遊パスを 3 セット購入し、8 日間すべてにおいて 1 日周遊パスを利用したときに最小となります。
答えが 32 bit 整数型に収まらないことがあることに注意してください。
Score : 300 points
Problem Statement
Takahashi is planning an N-day train trip.
For each day, he can pay the regular fare or use a one-day pass.
Here, for 1\leq i\leq N, the regular fare for the i-th day of the trip is F_i yen.
On the other hand, a batch of D one-day passes is sold for P yen. You can buy as many passes as you want, but only in units of D.
Each purchased pass can be used on any day, and it is fine to have some leftovers at the end of the trip.
Find the minimum possible total cost for the N-day trip, that is, the cost of purchasing one-day passes plus the total regular fare for the days not covered by one-day passes.
Constraints
- 1\leq N\leq 2\times 10^5
- 1\leq D\leq 2\times 10^5
- 1\leq P\leq 10^9
- 1\leq F_i\leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N D P F_1 F_2 \ldots F_N
Output
Print the minimum possible total cost for the N-day trip.
Sample Input 1
5 2 10 7 1 6 3 6
Sample Output 1
20
If he buys just one batch of one-day passes and uses them for the first and third days, the total cost will be (10\times 1)+(0+1+0+3+6)=20, which is the minimum cost needed.
Thus, print 20.
Sample Input 2
3 1 10 1 2 3
Sample Output 2
6
The minimum cost is achieved by paying the regular fare for all three days.
Sample Input 3
8 3 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
Sample Output 3
3000000000
The minimum cost is achieved by buying three batches of one-day passes and using them for all eight days.
Note that the answer may not fit into a 32-bit integer type.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
H \times W 枚のクッキーが H 行 W 列に並んでいます。
上から i 行目・左から j 列目のクッキーの色は英小文字 c_{i,j} で表されます。
これから、以下の手続きを行います。
1. 各行に対して次の操作を行う : その行に 2 枚以上のクッキーが残っており、それらの色がすべて同じならば、それらに印をつける。
2. 各列に対して次の操作を行う : その列に 2 枚以上のクッキーが残っており、それらの色がすべて同じならば、それらに印をつける。
3. 印のついたクッキーがあればそれらをすべて取り除いて 1. に戻り、なければ手続きを終了する。
手続きを終了した時点で残っているクッキーの枚数を求めてください。
制約
- 2 \leq H, W \leq 2000
- c_{i,j} は英小文字である
入力
入力は以下の形式で標準入力から与えられる。
H W
c_{1,1}c_{1,2} \ldots c_{1,W}
c_{2,1}c_{2,2} \ldots c_{2,W}
\vdots
c_{H,1}c_{H,2} \ldots c_{H,W}
出力
答えを出力せよ。
入力例 1
4 3 aaa aaa abc abd
出力例 1
2
以下で示す順で手続きを行います。
- 1. により、1, 2 行目のクッキーに印をつける。
- 2. により、1 列目のクッキーに印をつける。
- 3. により、印を付けたクッキーを取り除く。
この時点でクッキーは以下のようになっています。ただし、クッキーを取り除いた箇所は . で表しています。
... ... .bc .bd
- 1. により、何もしない。
- 2. により、2 列目のクッキーに印をつける。
- 3. により、印を付けたクッキーを取り除く。
この時点でクッキーは以下のようになっています。ただし、クッキーを取り除いた箇所は . で表しています。
... ... ..c ..d
- 1. により、何もしない。
- 2. により、何もしない。
- 3. により、印がついているクッキーが存在しないので手続きを終了する。
最終的に残っているクッキーの枚数は 2 枚です。
入力例 2
2 5 aaaaa abcde
出力例 2
4
入力例 3
3 3 ooo ooo ooo
出力例 3
0
Score : 400 points
Problem Statement
There are H \times W cookies in H rows and W columns.
The color of the cookie at the i-row from the top and j-th column from the left is represented by a lowercase English letter c_{i,j}.
We will perform the following procedure.
1. For each row, perform the following operation: if there are two or more cookies remaining in the row and they all have the same color, mark them.
2. For each column, perform the following operation: if there are two or more cookies remaining in the column and they all have the same color, mark them.
3. If there are any marked cookies, remove them all and return to 1; otherwise, terminate the procedure.
Find the number of cookies remaining at the end of the procedure.
Constraints
- 2 \leq H, W \leq 2000
- c_{i,j} is a lowercase English letter.
Input
The input is given from Standard Input in the following format:
H W
c_{1,1}c_{1,2} \ldots c_{1,W}
c_{2,1}c_{2,2} \ldots c_{2,W}
\vdots
c_{H,1}c_{H,2} \ldots c_{H,W}
Output
Print the answer.
Sample Input 1
4 3 aaa aaa abc abd
Sample Output 1
2
The procedure is performed as follows.
- 1. Mark the cookies in the first and second rows.
- 2. Mark the cookies in the first column.
- 3. Remove the marked cookies.
At this point, the cookies look like the following, where . indicates a position where the cookie has been removed.
... ... .bc .bd
- 1. Do nothing.
- 2. Mark the cookies in the second column.
- 3. Remove the marked cookies.
At this point, the cookies look like the following, where . indicates a position where the cookie has been removed.
... ... ..c ..d
- 1. Do nothing.
- 2. Do nothing.
- 3. No cookies are marked, so terminate the procedure.
The final number of cookies remaining is 2.
Sample Input 2
2 5 aaaaa abcde
Sample Output 2
4
Sample Input 3
3 3 ooo ooo ooo
Sample Output 3
0
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
最初 N 頂点 0 辺の無向グラフがあり、各頂点には 1 から N まで番号がついています。
Q 個のクエリが与えられるので、順に処理し、各クエリの後における「他のどの頂点とも辺で結ばれていない頂点」の数を出力してください。
i 個目のクエリは \mathrm{query}_i であり、各クエリは次の 2 種類いずれかです。
-
1 u v: 頂点 u と頂点 v を辺で結ぶ。このクエリが与えられる直前の時点で、頂点 u と頂点 v は辺で結ばれていない事が保証される。 -
2 v: 頂点 v と他の頂点を結ぶ辺をすべて削除する。(頂点 v 自体は削除しない。)
制約
- 2 \leq N\leq 3\times 10^5
- 1 \leq Q\leq 3\times 10^5
- 1 番目の種類のクエリにおいて、1\leq u,v\leq N, u\neq v
- 2 番目の種類のクエリにおいて、1\leq v\leq N
- 1 番目の種類のクエリの直前の時点で、そのクエリの u,v について頂点 u と頂点 v は辺で結ばれていない。
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
出力
Q 行出力せよ。
i 行目 (1\leq i\leq Q) には、i 個目のクエリを処理した後の「他のどの頂点とも辺で結ばれていない頂点」の数を出力せよ。
入力例 1
3 7 1 1 2 1 1 3 1 2 3 2 1 1 1 2 2 2 1 1 2
出力例 1
1 0 0 1 0 3 1
1 個目のクエリの後で、頂点 1 と頂点 2 は互いに結ばれており、頂点 3 のみが他のどの頂点とも辺で結ばれていません。
よって、1 行目には 1 を出力します。
また、3 個目のクエリの後でどの相異なる 2 頂点の間も辺で結ばれていますが、4 個目のクエリによって、
頂点 1 と他の頂点を結ぶ辺、すなわち 頂点 1 と頂点 2 を結ぶ辺および頂点 1 と頂点 3 を結ぶ辺が削除されます。
この結果として、頂点 2 と頂点 3 は互いに結ばれているが、頂点 1 は他のどの頂点とも辺で結ばれていない状態となります。
よって、3 行目には 0 を、4 行目には 1 を出力します。
入力例 2
2 1 2 1
出力例 2
2
2 番目の種類のクエリを行う直前の時点で、すでにその頂点と他の頂点を結ぶ辺が 1 本も存在しないこともあります。
Score : 425 points
Problem Statement
There is an undirected graph with N vertices numbered 1 through N, and initially with 0 edges.
Given Q queries, process them in order. After processing each query,
print the number of vertices that are not connected to any other vertices by an edge.
The i-th query, \mathrm{query}_i, is of one of the following two kinds.
-
1 u v: connect vertex u and vertex v with an edge. It is guaranteed that, when this query is given, vertex u and vertex v are not connected by an edge. -
2 v: remove all edges that connect vertex v and the other vertices. (Vertex v itself is not removed.)
Constraints
- 2 \leq N\leq 3\times 10^5
- 1 \leq Q\leq 3\times 10^5
- For each query of the first kind, 1\leq u,v\leq N and u\neq v.
- For each query of the second kind, 1\leq v\leq N.
- Right before a query of the first kind is given, there is no edge between vertices u and v.
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
Output
Print Q lines.
The i-th line (1\leq i\leq Q) should contain the number of vertices that are not connected to any other vertices by an edge.
Sample Input 1
3 7 1 1 2 1 1 3 1 2 3 2 1 1 1 2 2 2 1 1 2
Sample Output 1
1 0 0 1 0 3 1
After the first query, vertex 1 and vertex 2 are connected to each other by an edge, but vertex 3 is not connected to any other vertices.
Thus, 1 should be printed in the first line.
After the third query, all pairs of different vertices are connected by an edge.
However, the fourth query asks to remove all edges that connect vertex 1 and the other vertices, specifically to remove the edge between vertex 1 and vertex 2, and another between vertex 1 and vertex 3.
As a result, vertex 2 and vertex 3 are connected to each other, while vertex 1 is not connected to any other vertices by an edge.
Thus, 0 and 1 should be printed in the third and fourth lines, respectively.
Sample Input 2
2 1 2 1
Sample Output 2
2
When the query of the second kind is given, there may be no edge that connects that vertex and the other vertices.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 550 点
問題文
N 個の長さ M の数列 A_1, A_2, \ldots, A_N があります。i 番目の数列は M 個の整数 A_{i,1}, A_{i,2}, \ldots, A_{i,M} で表されます。
それぞれの長さが M の数列 X,Y について、X_i = Y_i となるような i(1 \leq i \leq M) の個数が奇数であるときに、X と Y は似ていると言います。
1 \leq i < j \leq N を満たす整数の組 (i,j) のうち、A_i と A_j が似ているものの個数を求めてください。
制約
- 1 \leq N \leq 2000
- 1 \leq M \leq 2000
- 1 \leq A_{i,j} \leq 999
- 入力は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
N M
A_{1,1} A_{1,2} \ldots A_{1,M}
A_{2,1} A_{2,2} \ldots A_{2,M}
\vdots
A_{N,1} A_{N,2} \ldots A_{N,M}
出力
答えを整数として出力せよ。
入力例 1
3 3 1 2 3 1 3 4 2 3 4
出力例 1
1
(i,j) = (1,2) は条件を満たします。なぜならば、A_{1,k} = A_{2,k} となるような k は k=1 の 1 個だけだからです。
(i,j) = (1,3) ,(2,3) は条件を満たさないため、条件を満たす (i,j) の組は (1,2) だけです。
入力例 2
6 5 8 27 27 10 24 27 8 2 4 5 15 27 26 17 24 27 27 27 27 27 27 7 22 11 27 19 27 27 27 27
出力例 2
5
Score: 550 points
Problem Statement
There are N sequences of length M, denoted as A_1, A_2, \ldots, A_N. The i-th sequence is represented by M integers A_{i,1}, A_{i,2}, \ldots, A_{i,M}.
Two sequences X and Y of length M are said to be similar if and only if the number of indices i (1 \leq i \leq M) such that X_i = Y_i is odd.
Find the number of pairs of integers (i,j) satisfying 1 \leq i < j \leq N such that A_i and A_j are similar.
Constraints
- 1 \leq N \leq 2000
- 1 \leq M \leq 2000
- 1 \leq A_{i,j} \leq 999
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M
A_{1,1} A_{1,2} \ldots A_{1,M}
A_{2,1} A_{2,2} \ldots A_{2,M}
\vdots
A_{N,1} A_{N,2} \ldots A_{N,M}
Output
Print the answer as an integer.
Sample Input 1
3 3 1 2 3 1 3 4 2 3 4
Sample Output 1
1
The pair (i,j) = (1,2) satisfies the condition because there is only one index k such that A_{1,k} = A_{2,k}, which is k=1.
The pairs (i,j) = (1,3), (2,3) do not satisfy the condition, making (1,2) the only pair that does.
Sample Input 2
6 5 8 27 27 10 24 27 8 2 4 5 15 27 26 17 24 27 27 27 27 27 27 7 22 11 27 19 27 27 27 27
Sample Output 2
5