実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
1 から N の番号が付けられた N 人の人がおり、この中で一対一の勝敗のつくゲームを何度か行いました。N 人は最初にそれぞれ持ち点として 0 を持っており、各ゲームでは勝者の持ち点が 1 増え、敗者の持ち点が 1 減ります(持ち点が負になることもあります)。最終的に人 i\ (1\leq i\leq N-1) の持ち点が A_i になったとき、人 N の持ち点を求めてください。なお、ゲームの進行によらず最終的な人 N の持ち点は一意に定まることが示せます。
制約
- 2\leq N\leq 100
- -100\leq A_i\leq 100
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
A_1 A_2 \ldots A_{N-1}
出力
答えを出力せよ。
入力例 1
4 1 -2 -1
出力例 1
2
最終的に人 1,2,3 の持ち点が 1,-2,-1 となるような進行として、例えば次のようなものが考えられます。
- 最初、人 1,2,3,4 の持ち点はそれぞれ 0,0,0,0 である。
- 人 1 と 2 が対戦して、人 1 が勝利する。4 人の持ち点はそれぞれ 1,-1,0,0 である。
- 人 1 と 4 が対戦して、人 4 が勝利する。4 人の持ち点はそれぞれ 0,-1,0,1 である。
- 人 1 と 2 が対戦して、人 1 が勝利する。4 人の持ち点はそれぞれ 1,-2,0,1 である。
- 人 2 と 3 が対戦して、人 2 が勝利する。4 人の持ち点はそれぞれ 1,-1,-1,1 である。
- 人 2 と 4 が対戦して、人 4 が勝利する。4 人の持ち点はそれぞれ 1,-2,-1,2 である。
この場合、人 4 の持ち点は 2 になります。ほかにも別の進行が考えられますが、どのような進行であっても人 4 の持ち点は 2 になります。
入力例 2
3 0 0
出力例 2
0
入力例 3
6 10 20 30 40 50
出力例 3
-150
Score: 100 points
Problem Statement
There are N people labeled 1 to N, who have played several one-on-one games without draws. Initially, each person started with 0 points. In each game, the winner's score increased by 1 and the loser's score decreased by 1 (scores can become negative). Determine the final score of person N if the final score of person i\ (1\leq i\leq N-1) is A_i. It can be shown that the final score of person N is uniquely determined regardless of the sequence of games.
Constraints
- 2 \leq N \leq 100
- -100 \leq A_i \leq 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_{N-1}
Output
Print the answer.
Sample Input 1
4 1 -2 -1
Sample Output 1
2
Here is one possible sequence of games where the final scores of persons 1, 2, 3 are 1, -2, -1, respectively.
- Initially, persons 1, 2, 3, 4 have 0, 0, 0, 0 points, respectively.
- Persons 1 and 2 play, and person 1 wins. The players now have 1, -1, 0, 0 point(s).
- Persons 1 and 4 play, and person 4 wins. The players now have 0, -1, 0, 1 point(s).
- Persons 1 and 2 play, and person 1 wins. The players now have 1, -2, 0, 1 point(s).
- Persons 2 and 3 play, and person 2 wins. The players now have 1, -1, -1, 1 point(s).
- Persons 2 and 4 play, and person 4 wins. The players now have 1, -2, -1, 2 point(s).
In this case, the final score of person 4 is 2. Other possible sequences of games exist, but the score of person 4 will always be 2 regardless of the progression.
Sample Input 2
3 0 0
Sample Output 2
0
Sample Input 3
6 10 20 30 40 50
Sample Output 3
-150
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
下の画像で示す図において、a 番の点と b 番の点が線で直接結ばれているかを答えてください。

制約
- 1 \leq a \lt b \leq 10
- a, b は整数
入力
入力は以下の形式で標準入力から与えられる。
a b
出力
a 番の点と b 番の点が線で直接結ばれている場合は Yes を出力し、結ばれていない場合は No を出力せよ。
ジャッジは英大文字と英小文字を厳密に区別することに注意せよ。
入力例 1
4 5
出力例 1
Yes
問題文で示した図において、4 番の点と 5 番の点は線で直接結ばれています。
よって、Yes を出力します。
入力例 2
3 5
出力例 2
No
問題文で示した図において、3 番の点と 5 番の点は線で直接結ばれていません。
よって、No を出力します。
入力例 3
1 10
出力例 3
Yes
Score : 100 points
Problem Statement
In the figure shown in the image below, are the points numbered a and b directly connected by a line segment?

Constraints
- 1 \leq a \lt b \leq 10
- a and b are integers.
Input
Input is given from Standard Input in the following format:
a b
Output
If the points numbered a and b are directly connected by a line segment, print Yes; otherwise, print No.
The judge is case-sensitive: be sure to print uppercase and lowercase letters correctly.
Sample Input 1
4 5
Sample Output 1
Yes
In the figure shown in the Problem Statement, the points numbered 4 and 5 are directly connected by a line segment.
Thus, Yes should be printed.
Sample Input 2
3 5
Sample Output 2
No
In the figure shown in the Problem Statement, the points numbered 3 and 5 are not directly connected by a line segment.
Thus, No should be printed.
Sample Input 3
1 10
Sample Output 3
Yes
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
1 から N の番号がついた N 人の人がいます。
人 i はキーエンス本社ビルの建築面積を S_i 平方メートルであると予想しました。
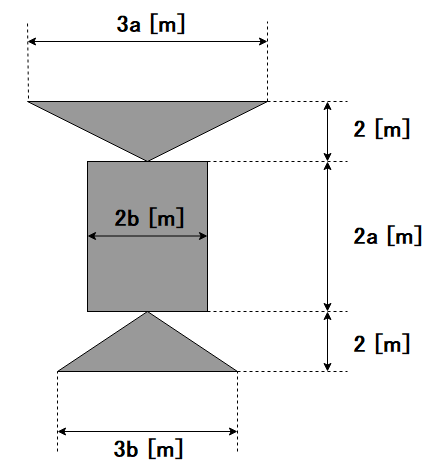
キーエンス本社ビルは下図のような形をしています。ただし、a,b はある 正の整数 です。
つまり、キーエンス本社ビルの建築面積は 4ab+3a+3b 平方メートルと表されます。
N 人のうち、この情報のみによって、予想した面積が確実に誤りであるとわかる人数を求めてください。
制約
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N S_1 \ldots S_N
出力
答えを出力せよ。
入力例 1
3 10 20 39
出力例 1
1
a=1,b=1 のとき面積は 10 平方メートル、a=2,b=3 のとき面積は 39 平方メートルとなります。
しかし a,b がどのような正の整数であったとしても面積が 20 平方メートルになることはありません。
よって、人 2 の予想だけは確実に誤りであることがわかります。
入力例 2
5 666 777 888 777 666
出力例 2
3
Score : 200 points
Problem Statement
There are N people numbered 1 to N.
Person i guessed the building area of KEYENCE headquarters building to be S_i square meters.
The shape of KEYENCE headquarters building is shown below, where a and b are some positive integers.
That is, the building area of the building can be represented as 4ab+3a+3b.
Based on just this information, how many of the N people are guaranteed to be wrong in their guesses?

Constraints
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N S_1 \ldots S_N
Output
Print the answer.
Sample Input 1
3 10 20 39
Sample Output 1
1
The area would be 10 square meters if a=1,b=1, and 39 square meters if a=2,b=3.
However, no pair of positive integers a and b would make the area 20 square meters.
Thus, we can only be sure that Person 2 guessed wrong.
Sample Input 2
5 666 777 888 777 666
Sample Output 2
3
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
xy 平面上に N 人の人 1,2,\dots,N がおり、人 i は座標 (X_i,Y_i) にいます。
このうち、 K 人の人 A_1,A_2,\dots,A_K に同じ強さの明かりを持たせます。
座標 (x,y) にいる人が強さ R の明かりを持っている時、その明かりによって中心 (x,y) 、半径 R の円の内部全体(境界を含む)が照らされます。
すべての人が少なくとも 1 つの明かりによって照らされるために必要な明かりの強さの最小値を求めてください。
制約
- 入力は全て整数
- 1 \le K < N \le 1000
- 1 \le A_1 < A_2 < \dots < A_K \le N
- |X_i|,|Y_i| \le 10^5
- i \neq j ならば (X_i,Y_i) \neq (X_j,Y_j)
入力
入力は以下の形式で標準入力から与えられる。
N K A_1 A_2 \dots A_K X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
出力
答えを実数として出力せよ。
出力された解と想定解との絶対誤差または相対誤差が 10^{-5} 以下であるならば、出力は正しいと見なされる。
入力例 1
4 2 2 3 0 0 0 1 1 2 2 0
出力例 1
2.23606797749978969
この入力では人が 4 人おり、そのうち人 2,3 が明かりを持ちます。
R \ge \sqrt{5} \approx 2.236068 である時、すべての人が少なくとも 1 つの明かりによって照らされます。
入力例 2
2 1 2 -100000 -100000 100000 100000
出力例 2
282842.712474619009
入力例 3
8 3 2 6 8 -17683 17993 93038 47074 58079 -57520 -41515 -89802 -72739 68805 24324 -73073 71049 72103 47863 19268
出力例 3
130379.280458974768
Score : 200 points
Problem Statement
There are N people numbered 1, 2, \dots, N in the xy-plane. Person i is at the coordinates (X_i, Y_i).
K of these people, Persons A_1, A_2, \dots, A_K, will receive lights of the same strength.
When a person at coordinates (x, y) has a light of strength R, it lights up the interior of a circle of radius R centered at (x, y) (including the boundary).
Find the minimum strength of the lights needed for every person to be lit by at least one light.
Constraints
- All values in input are integers.
- 1 \le K < N \le 1000
- 1 \le A_1 < A_2 < \dots < A_K \le N
- |X_i|,|Y_i| \le 10^5
- (X_i,Y_i) \neq (X_j,Y_j), if i \neq j.
Input
Input is given from Standard Input in the following format:
N K A_1 A_2 \dots A_K X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
Output
Print the answer as a real number.
Your output will be considered correct if its absolute or relative error from the judge's output is at most 10^{-5}.
Sample Input 1
4 2 2 3 0 0 0 1 1 2 2 0
Sample Output 1
2.23606797749978969
This input contains four people. Among them, Persons 2 and 3 will have lights.
Every person will be lit by at least one light if R \ge \sqrt{5} \approx 2.236068.
Sample Input 2
2 1 2 -100000 -100000 100000 100000
Sample Output 2
282842.712474619009
Sample Input 3
8 3 2 6 8 -17683 17993 93038 47074 58079 -57520 -41515 -89802 -72739 68805 24324 -73073 71049 72103 47863 19268
Sample Output 3
130379.280458974768
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
長さ N の数列 A = (a_1, a_2, \dots, a_N) があります。
以下で説明される Q 個のクエリに答えてください。
- クエリ i : 整数の組 (x_i, k_i) が与えられます。A の要素を a_1, a_2, \dots と前から順に見ていったときに、数 x_i が k_i 回目に登場するのは A の前から何番目の要素を見たときかを出力してください。
ただし条件を満たす要素が存在しない場合は -1 を出力してください。
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq Q \leq 2 \times 10^5
- 0 \leq a_i \leq 10^9 (1 \leq i \leq N)
- 0 \leq x_i \leq 10^9 (1 \leq i \leq Q)
- 1 \leq k_i \leq N (1 \leq i \leq Q)
- 入力はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N Q a_1 a_2 \dots a_N x_1 k_1 x_2 k_2 \vdots x_Q k_Q
出力
Q 行出力せよ。i 行目ではクエリ i に対する答えを出力せよ。
入力例 1
6 8 1 1 2 3 1 2 1 1 1 2 1 3 1 4 2 1 2 2 2 3 4 1
出力例 1
1 2 5 -1 3 6 -1 -1
A の中で 1 は a_1, a_2, a_5 に登場します。よって、クエリ 1 からクエリ 4 の答えは順に 1, 2, 5, -1 となります。
入力例 2
3 2 0 1000000000 999999999 1000000000 1 123456789 1
出力例 2
2 -1
Score : 300 points
Problem Statement
We have a sequence of N numbers: A = (a_1, a_2, \dots, a_N).
Process the Q queries explained below.
- Query i: You are given a pair of integers (x_i, k_i). Let us look at the elements of A one by one from the beginning: a_1, a_2, \dots Which element will be the k_i-th occurrence of the number x_i?
Print the index of that element, or -1 if there is no such element.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq Q \leq 2 \times 10^5
- 0 \leq a_i \leq 10^9 (1 \leq i \leq N)
- 0 \leq x_i \leq 10^9 (1 \leq i \leq Q)
- 1 \leq k_i \leq N (1 \leq i \leq Q)
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N Q a_1 a_2 \dots a_N x_1 k_1 x_2 k_2 \vdots x_Q k_Q
Output
Print Q lines. The i-th line should contain the answer to Query i.
Sample Input 1
6 8 1 1 2 3 1 2 1 1 1 2 1 3 1 4 2 1 2 2 2 3 4 1
Sample Output 1
1 2 5 -1 3 6 -1 -1
1 occurs in A at a_1, a_2, a_5. Thus, the answers to Query 1 through 4 are 1, 2, 5, -1 in this order.
Sample Input 2
3 2 0 1000000000 999999999 1000000000 1 123456789 1
Sample Output 2
2 -1
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 250 点
問題文
N 種類のビーンズが 1 粒ずつあります。 i 種類目のビーンズはおいしさが A_i で色が C_i です。ビーンズは混ぜられており、色でしか区別することができません。
あなたはビーンズの色を 1 つ選び、その色のビーンズをどれか 1 粒食べます。ビーンズの色をうまく選ぶことで、食べる可能性のあるビーンズのおいしさの最小値を最大化してください。
制約
- 1 \leq N \leq 2 \times 10^{5}
- 1 \leq A_i \leq 10^{9}
- 1 \leq C_i \leq 10^{9}
- 入力は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 C_1 A_2 C_2 \vdots A_N C_N
出力
食べる可能性のあるビーンズのおいしさの最小値の最大値を整数として出力せよ。
入力例 1
4 100 1 20 5 30 5 40 1
出力例 1
40
同じ色のビーンズは互いに区別がつかないことに注意してください。
選ぶことができる色は 色 1 と 色 5 です。
- 色 1 のビーンズは 2 種類あり、美味しさはそれぞれ 100, 40 です。よって、色 1 を選んだときのおいしさの最小値は 40 です。
- 色 5 のビーンズは 2 種類あり、美味しさはそれぞれ 20, 30 です。よって、色 5 を選んだときのおいしさの最小値は 20 です。
おいしさの最小値を最大化するには 色 1 を選べばよいため、そのときの最小値である 40 を出力します。
入力例 2
10 68 3 17 2 99 2 92 4 82 4 10 3 100 2 78 1 3 1 35 4
出力例 2
35
Score: 250 points
Problem Statement
There are N types of beans, one bean of each type. The i-th type of bean has a deliciousness of A_i and a color of C_i. The beans are mixed and can only be distinguished by color.
You will choose one color of beans and eat one bean of that color. By selecting the optimal color, maximize the minimum possible deliciousness of the bean you eat.
Constraints
- 1 \leq N \leq 2 \times 10^{5}
- 1 \leq A_i \leq 10^{9}
- 1 \leq C_i \leq 10^{9}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 C_1 A_2 C_2 \vdots A_N C_N
Output
Print as an integer the maximum value of the minimum possible deliciousness of the bean you eat.
Sample Input 1
4 100 1 20 5 30 5 40 1
Sample Output 1
40
Note that beans of the same color cannot be distinguished from each other.
You can choose color 1 or color 5.
- There are two types of beans of color 1, with deliciousness of 100 and 40. Thus, the minimum deliciousness when choosing color 1 is 40.
- There are two types of beans of color 5, with deliciousness of 20 and 30. Thus, the minimum deliciousness when choosing color 5 is 20.
To maximize the minimum deliciousness, you should choose color 1, so print the minimum deliciousness in that case: 40.
Sample Input 2
10 68 3 17 2 99 2 92 4 82 4 10 3 100 2 78 1 3 1 35 4
Sample Output 2
35
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
T 個のテストケースについて、以下の問題を解いてください。
非負整数 a,s が与えられます。以下の条件を両方とも満たす非負整数の組 (x,y) は存在しますか?
- x\ \text{AND}\ y=a
- x+y=s
\text{AND} とは
非負整数 n, m の bit ごとの論理積 n\ \text{AND}\ m は、以下のように定義されます。
- n\ \text{AND}\ m を二進表記した際の 2^k \, (k \geq 0) の位の数は、n, m を二進表記した際の 2^k の位の数のうち両方が 1 であれば 1、そうでなければ 0 である。
制約
- 1 \leq T \leq 10^5
- 0 \leq a,s \lt 2^{60}
- 入力はすべて整数
入力
入力は標準入力から与えられる。入力の 1 行目は以下の形式である。
T
その後、 T 個のテストケースが続く。各テストケースは以下の形式で与えられる。
a s
出力
T 行出力せよ。i\ (1 \leq i \leq T) 行目には、i 番目に与えられるテストケースについて問題文中の条件を両方とも満たす非負整数の組 (x,y) が存在するなら Yes を、存在しないなら No を出力せよ。
入力例 1
2 1 8 4 2
出力例 1
Yes No
1 番目のテストケースにおいては、(x,y)=(3,5) などが条件を満たします。
2 番目のテストケースにおいては、条件を満たす非負整数の組 (x,y) は存在しません。
入力例 2
4 201408139683277485 381410962404666524 360288799186493714 788806911317182736 18999951915747344 451273909320288229 962424162689761932 1097438793187620758
出力例 2
No Yes Yes No
Score : 400 points
Problem Statement
Solve the following problem for T test cases.
Given are non-negative integers a and s. Is there a pair of non-negative integers (x,y) that satisfies both of the conditions below?
- x\ \text{AND}\ y=a
- x+y=s
What is bitwise \mathrm{AND}?
The bitwise \mathrm{AND} of integers A and B, A\ \mathrm{AND}\ B, is defined as follows:
- When A\ \mathrm{AND}\ B is written in base two, the digit in the 2^k's place (k \geq 0) is 1 if those of A and B are both 1, and 0 otherwise.
Constraints
- 1 \leq T \leq 10^5
- 0 \leq a,s \lt 2^{60}
- All values in input are integers.
Input
Input is given from Standard Input. The first line is in the following format:
T
Then, T test cases follow. Each test case is in the following format:
a s
Output
Print T lines. The i-th line (1 \leq i \leq T) should contain Yes if, in the i-th test case, there is a pair of non-negative integers (x,y) that satisfies both of the conditions in the Problem Statement, and No otherwise.
Sample Input 1
2 1 8 4 2
Sample Output 1
Yes No
In the first test case, some pairs such as (x,y)=(3,5) satisfy the conditions.
In the second test case, no pair of non-negative integers satisfies the conditions.
Sample Input 2
4 201408139683277485 381410962404666524 360288799186493714 788806911317182736 18999951915747344 451273909320288229 962424162689761932 1097438793187620758
Sample Output 2
No Yes Yes No
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 450 点
問題文
「ユ木」を、以下の手順で生成することができる木と定義します。
- 正整数 x,y を選ぶ
- 頂点を 1 つ用意する
- 別に x 個の頂点を用意し、それぞれを手順 2 で用意した頂点と辺で結ぶ
- 手順 3 で用意した x 個の頂点それぞれに、 y 個の葉をつける
x=4,y=2 のユ木を下図に示します。手順 2,3,4 で用意される頂点をそれぞれ赤、青、緑で示しています。

N 頂点の木 T が与えられます。頂点には 1 から N の番号が付けられており、 i\;(=1,2,\dots,N-1) 番目の辺は頂点 u_i と頂点 v_i を結びます。
T の 0 個以上の頂点とそれに隣接する辺を削除して 1 つのユ木にするとき、削除する頂点数の最小値を求めてください。なお、本問題の制約下で、T をかならずユ木にすることができます。
制約
- 3 \leq N \leq 3 \times 10^5
- 1 \leq u_i < v_i \leq N
- 与えられるグラフは木である
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
出力
答えを出力せよ。
入力例 1
8 1 3 2 3 3 4 4 5 5 6 5 7 4 8
出力例 1
1
頂点 8 を削除することで、与えられた木を x=2,y=2 のユ木にすることができます。
入力例 2
3 1 2 2 3
出力例 2
0
与えられた木はすでに x=1,y=1 のユ木です。
入力例 3
10 1 3 1 2 5 7 6 10 2 8 1 6 8 9 2 7 1 4
出力例 3
3
Score : 450 points
Problem Statement
A "Snowflake Tree" is defined as a tree that can be generated by the following procedure:
- Choose positive integers x,y.
- Prepare one vertex.
- Prepare x more vertices, and connect each of them to the vertex prepared in step 2.
- For each of the x vertices prepared in step 3, attach y leaves to it.
The figure below shows a Snowflake Tree with x=4,y=2. The vertices prepared in steps 2, 3, 4 are shown in red, blue, and green, respectively.

You are given a tree T with N vertices. The vertices are numbered 1 to N, and the i-th edge (i=1,2,\dots,N-1) connects vertices u_i and v_i.
Consider deleting zero or more vertices of T and the edges adjacent to them so that the remaining graph becomes a single Snowflake Tree. Find the minimum number of vertices that must be deleted. Under the constraints of this problem, it is always possible to transform T into a Snowflake Tree.
Constraints
- 3 \leq N \leq 3 \times 10^5
- 1 \leq u_i < v_i \leq N
- The given graph is a tree.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
Output
Print the answer.
Sample Input 1
8 1 3 2 3 3 4 4 5 5 6 5 7 4 8
Sample Output 1
1
By deleting vertex 8, the given tree can be transformed into a Snowflake Tree with x=2,y=2.
Sample Input 2
3 1 2 2 3
Sample Output 2
0
The given tree is already a Snowflake Tree with x=1,y=1.
Sample Input 3
10 1 3 1 2 5 7 6 10 2 8 1 6 8 9 2 7 1 4
Sample Output 3
3
実行時間制限: 3.5 sec / メモリ制限: 1024 MiB
配点 : 525 点
問題文
あなたの前に体力 H のモンスターが現れ、ターン制の戦闘が開始しました。
あなたは、ターン 1,2,… のそれぞれに呪文 1,…,N の N 種類の呪文のうち一つを唱えます。
ターン i に呪文 j を唱えると、その呪文の効果としてターン i,i+1,…,i+t_j -1 のそれぞれでモンスターの体力が d_j 減ります。
モンスターの体力を 0 以下にすることが可能な最も早いターンを求めてください。
制約
- 1 \leq N \leq 3 \times 10^5
- 1 \leq H \leq 10^{18}
- 1 \leq t_i,d_i \leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N H t_1 d_1 \vdots t_N d_N
出力
答えを出力せよ。
入力例 1
2 20 2 2 5 1
出力例 1
6
以下のようにするとターン 6 にモンスターの体力を 0 以下に出来ます。これが最も早いターンです。
- ターン 1 に魔法 1 を使う。ターン 1 に使った魔法の効果でモンスターの体力が 2 減り、18 になる。
- ターン 2 に魔法 2 を使う。ターン 1,2 に使った魔法の効果でモンスターの体力が 2+1=3 減り、15 になる。
- ターン 3 に魔法 1 を使う。ターン 2,3 に使った魔法の効果でモンスターの体力が 1+2=3 減り、12 になる。
- ターン 4 に魔法 2 を使う。ターン 2,3,4 に使った魔法の効果でモンスターの体力が 1+2+1=4 減り、8 になる。
- ターン 5 に魔法 1 を使う。ターン 2,4,5 に使った魔法の効果でモンスターの体力が 1+1+2=4 減り、4 になる。
- ターン 6 に魔法 2 を使う。ターン 2,4,5,6 に使った魔法の効果でモンスターの体力が 1+1+2+1=5 減り、-1 になる。
入力例 2
10 200 1 21 1 1 1 1 8 4 30 1 3 1 10 2 8 1 9 1 4 4
出力例 2
9
Score : 525 points
Problem Statement
A monster with health H has appeared in front of you, and a turn-based battle has started.
In each turn 1,2,…, you cast one of N spells, spells 1,…,N.
If you cast spell i in turn j, the monster's health reduces by d_i in each turn j,j+1,…,j+t_i -1.
Find the earliest turn that you can make the monster's health 0 or less.
Constraints
- 1 \leq N \leq 3 \times 10^5
- 1 \leq H \leq 10^{18}
- 1 \leq t_i,d_i \leq 10^9
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N H t_1 d_1 \vdots t_N d_N
Output
Print the answer.
Sample Input 1
2 20 2 2 5 1
Sample Output 1
6
The following procedure makes the monster's health 0 or less in turn 6, which is the earliest.
- Cast spell 1 in turn 1. Due to the spell cast in turn 1, the monster's health reduces by 2 and becomes 18.
- Cast spell 2 in turn 2. Due to the spells cast in turns 1 and 2, the monster's health reduces by 2+1=3 and becomes 15.
- Cast spell 1 in turn 3. Due to the spells cast in turns 2 and 3, the monster's health reduces by 1+2=3 and becomes 12.
- Cast spell 2 in turn 4. Due to the spells cast in turns 2,3 and 4, the monster's health reduces by 1+2+1=4 and becomes 8.
- Cast spell 1 in turn 5. Due to the spells cast in turns 2,4 and 5, the monster's health reduces by 1+1+2=4 and becomes 4.
- Cast spell 2 in turn 6. Due to the spells cast in turns 2,4,5 and 6, the monster's health reduces by 1+1+2+1=5 and becomes -1.
Sample Input 2
10 200 1 21 1 1 1 1 8 4 30 1 3 1 10 2 8 1 9 1 4 4
Sample Output 2
9