Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
3 つの数字 x,y,z をこの順に並べてできる 3 桁の整数を xyz と表すことにします。
どの桁も 0 でない 3 桁の整数 abc が与えられるので、abc+bca+cab を求めてください。
制約
- abc は どの桁も 0 でない 3 桁の整数
入力
入力は以下の形式で標準入力から与えられる。
abc
出力
答えを出力せよ。
入力例 1
123
出力例 1
666
123+231+312=666 となります。
入力例 2
999
出力例 2
2997
999+999+999=2997 となります。
Score : 100 points
Problem Statement
Let xyz denote the 3-digit integer whose digits are x, y, z from left to right.
Given a 3-digit integer abc none of whose digits is 0, find abc+bca+cab.
Constraints
- abc is a 3-digit integer abc none of whose digits is 0.
Input
Input is given from Standard Input in the following format:
abc
Output
Print the answer.
Sample Input 1
123
Sample Output 1
666
We have 123+231+312=666.
Sample Input 2
999
Sample Output 2
2997
We have 999+999+999=2997.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
正整数 N が与えられるので、
N 個の 0 と N+1 個の 1 からなる、0 と 1 が交互に並んだ文字列を出力してください。
制約
- N は整数
- 1 \leq N \leq 100
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを出力せよ。
入力例 1
4
出力例 1
101010101
4 個の 0 と 5 個の 1 からなる、0 と 1 が交互に並んだ文字列は 101010101 です。
入力例 2
1
出力例 2
101
入力例 3
10
出力例 3
101010101010101010101
Score: 100 points
Problem Statement
Given a positive integer N, print a string of N zeros and N+1 ones where 0 and 1 alternate.
Constraints
- N is an integer.
- 1 \leq N \leq 100
Input
The input is given from Standard Input in the following format:
N
Output
Print the answer.
Sample Input 1
4
Sample Output 1
101010101
A string of four zeros and five ones where 0 and 1 alternate is 101010101.
Sample Input 2
1
Sample Output 2
101
Sample Input 3
10
Sample Output 3
101010101010101010101
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
以下のような N 個の整数列 A_0,\ldots,A_{N-1} を求めてください。
- 各 i (0\leq i \leq N-1) について、A_i の長さは i+1 である。
-
各 i,j (0\leq i \leq N-1, 0 \leq j \leq i) について、A_i の j+1 番目の値 a_{i,j} は次のように定められる。
- j=0 または j=i の時、a_{i,j}=1
- それ以外の時、a_{i,j} = a_{i-1,j-1} + a_{i-1,j}
制約
- 1 \leq N \leq 30
- N は整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
N 行出力せよ。 i 行目には A_{i-1} の値を順に空白区切りで出力せよ。
入力例 1
3
出力例 1
1 1 1 1 2 1
入力例 2
10
出力例 2
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1
Score : 200 points
Problem Statement
Find the N integer sequences A_0,\ldots,A_{N-1} defined as follows.
- For each i (0\leq i \leq N-1), the length of A_i is i+1.
- For each i and j (0\leq i \leq N-1, 0 \leq j \leq i), the (j+1)-th term of A_i, denoted by a_{i,j}, is defined as follows.
- a_{i,j}=1, if j=0 or j=i.
- a_{i,j} = a_{i-1,j-1} + a_{i-1,j}, otherwise.
Constraints
- 1 \leq N \leq 30
- N is an integer.
Input
Input is given from Standard Input in the following format:
N
Output
Print N lines. The i-th line should contain the terms of A_{i-1} separated by spaces.
Sample Input 1
3
Sample Output 1
1 1 1 1 2 1
Sample Input 2
10
Sample Output 2
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
無限に長いピアノの鍵盤があります。 この鍵盤内の連続する区間であって、白鍵 W 個と黒鍵 B 個からなるものは存在しますか?
文字列 wbwbwwbwbwbw を無限に繰り返してできる文字列を S とおきます。
S の部分文字列であって、W 個の w と B 個の b からなるものは存在しますか?
S の部分文字列とは
S の部分文字列とは、ある 2 つの正整数 l,r\ (l\leq r) に対して、S の l 文字目、l+1 文字目、\dots、r 文字目をこの順に繋げてできる文字列のことをいいます。制約
- W,B は整数
- 0\leq W,B \leq 100
- W+B \geq 1
入力
入力は以下の形式で標準入力から与えられる。
W B
出力
S の部分文字列であって、W 個の w と B 個の b からなるものが存在するならば Yes を、存在しないならば No を出力せよ。
入力例 1
3 2
出力例 1
Yes
S の最初の 15 文字は wbwbwwbwbwbwwbw であり、S の 11 文字目から 15 文字目までを取り出してできる文字列 bwwbw は 3 個の w と 2 個の b からなる部分文字列の一例です。
入力例 2
3 0
出力例 2
No
3 個の w と 0 個の b からなる文字列は www のみですが、これは S の部分文字列ではありません。
入力例 3
92 66
出力例 3
Yes
Score: 200 points
Problem Statement
There is an infinitely long piano keyboard. Is there a continuous segment within this keyboard that consists of W white keys and B black keys?
Let S be the string formed by infinitely repeating the string wbwbwwbwbwbw.
Is there a substring of S that consists of W occurrences of w and B occurrences of b?
What is a substring of S?
A substring of S is a string that can be formed by concatenating the l-th, (l+1)-th, \dots, r-th characters of S in this order for some two positive integers l and r (l\leq r).Constraints
- W and B are integers.
- 0\leq W,B \leq 100
- W+B \geq 1
Input
The input is given from Standard Input in the following format:
W B
Output
If there is a substring of S that consists of W occurrences of w and B occurrences of b, print Yes; otherwise, print No.
Sample Input 1
3 2
Sample Output 1
Yes
The first 15 characters of S are wbwbwwbwbwbwwbw. You can take the 11-th through 15-th characters to form the string bwwbw, which is a substring consisting of three occurrences of w and two occurrences of b.
Sample Input 2
3 0
Sample Output 2
No
The only string consisting of three occurrences of w and zero occurrences of b is www, which is not a substring of S.
Sample Input 3
92 66
Sample Output 3
Yes
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
あなたはゲームをプレイしています。
N 人の敵が一列に並んでおり、前から i 番目の敵の体力は H_i です。
あなたは 0 で初期化された変数 T を使い、全ての敵の体力が 0 以下になるまで次の行動を繰り返します。
- T を 1 増やす。その後、体力が 1 以上である最も前の敵を攻撃する。このとき、T が 3 の倍数ならばその敵の体力は 3 減り、そうでないなら 1 減る。
全ての敵の体力が 0 以下になったときの T の値を求めてください。
制約
- 1 \leq N \leq 2\times 10^5
- 1 \leq H_i \leq 10^9
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N H_1 H_2 \ldots H_N
出力
答えを出力せよ。
入力例 1
3 6 2 2
出力例 1
8
行動は次のように行われます。
- T=1 になる。1 番目の敵を攻撃し、その敵の体力は 6-1=5 となる。
- T=2 になる。1 番目の敵を攻撃し、その敵の体力は 5-1=4 となる。
- T=3 になる。1 番目の敵を攻撃し、その敵の体力は 4-3=1 となる。
- T=4 になる。1 番目の敵を攻撃し、その敵の体力は 1-1=0 となる。
- T=5 になる。2 番目の敵を攻撃し、その敵の体力は 2-1=1 となる。
- T=6 になる。2 番目の敵を攻撃し、その敵の体力は 1-3=-2 となる。
- T=7 になる。3 番目の敵を攻撃し、その敵の体力は 2-1=1 となる。
- T=8 になる。3 番目の敵を攻撃し、その敵の体力は 1-1=0 となる。
入力例 2
9 1 12 123 1234 12345 123456 1234567 12345678 123456789
出力例 2
82304529
入力例 3
5 1000000000 1000000000 1000000000 1000000000 1000000000
出力例 3
3000000000
オーバーフローに注意してください。
Score : 300 points
Problem Statement
You are playing a game.
There are N enemies lined up in a row, and the i-th enemy from the front has a health of H_i.
You will repeat the following action until the healths of all enemies become 0 or less, using a variable T initialized to 0.
- Increase T by 1. Then, attack the frontmost enemy with health 1 or more. If T is a multiple of 3, the enemy's health decreases by 3; otherwise, it decreases by 1.
Find the value of T when the healths of all enemies become 0 or less.
Constraints
- 1 \leq N \leq 2\times 10^5
- 1 \leq H_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N H_1 H_2 \ldots H_N
Output
Print the answer.
Sample Input 1
3 6 2 2
Sample Output 1
8
The actions are performed as follows:
- T becomes 1. Attack the 1st enemy, and its health becomes 6-1=5.
- T becomes 2. Attack the 1st enemy, and its health becomes 5-1=4.
- T becomes 3. Attack the 1st enemy, and its health becomes 4-3=1.
- T becomes 4. Attack the 1st enemy, and its health becomes 1-1=0.
- T becomes 5. Attack the 2nd enemy, and its health becomes 2-1=1.
- T becomes 6. Attack the 2nd enemy, and its health becomes 1-3=-2.
- T becomes 7. Attack the 3rd enemy, and its health becomes 2-1=1.
- T becomes 8. Attack the 3rd enemy, and its health becomes 1-1=0.
Sample Input 2
9 1 12 123 1234 12345 123456 1234567 12345678 123456789
Sample Output 2
82304529
Sample Input 3
5 1000000000 1000000000 1000000000 1000000000 1000000000
Sample Output 3
3000000000
Beware of integer overflow.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
ある地方に、1 から N の番号がついた N 個の街と、1 から M の番号がついた M 本の道路があります。
i 番目の道路は街 A_i と街 B_i を双方向に結び、長さは C_i です。
好きな街からスタートして同じ街を二度以上通らずに別の街へ移動するときの、通る道路の長さの和としてありえる最大値を求めてください。
制約
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1\leq A_i < B_i \leq N
- (A_i,B_i) は相異なる
- 1\leq C_i \leq 10^8
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 C_1 \vdots A_M B_M C_M
出力
答えを出力せよ。
入力例 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
出力例 1
1110
4\to 1\to 3\to 2 と移動すると、通る道路の長さの和は 1110 となります。
入力例 2
10 1 5 9 1
出力例 2
1
道路と繋がっていない街が存在するかもしれません。
入力例 3
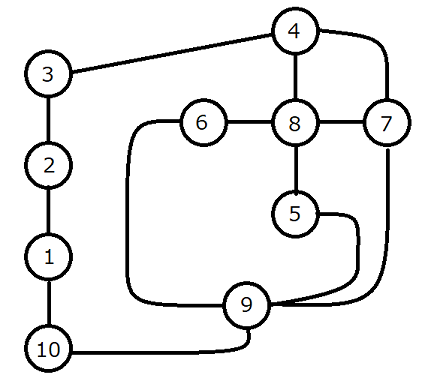
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
出力例 3
20
Score : 300 points
Problem Statement
A region has N towns numbered 1 to N, and M roads numbered 1 to M.
The i-th road connects town A_i and town B_i bidirectionally with length C_i.
Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.
Constraints
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1 \leq A_i < B_i \leq N
- The pairs (A_i,B_i) are distinct.
- 1\leq C_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 C_1 \vdots A_M B_M C_M
Output
Print the answer.
Sample Input 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
Sample Output 1
1110
If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.
Sample Input 2
10 1 5 9 1
Sample Output 2
1
There may be a town that is not connected to a road.
Sample Input 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
Sample Output 3
20

Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
ビル 1, ビル 2, \ldots, ビル N の N 棟のビルがこの順で一列に並んでいます。ビル i\ (1\leq i\leq N) の高さは H_i です。
各 i=1,2,\ldots,N について、次を満たす整数 j\ (i\lt j\leq N) の個数を求めてください。
- ビル i とビル j の間にビル j より高いビルが存在しない。
制約
- 1\leq N\leq 2\times 10^5
- 1\leq H_i\leq N
- H_i\neq H_j\ (i\neq j)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N H_1 H_2 \ldots H_N
出力
各 i=1,2,\ldots,N に対して条件を満たす j の個数を c_i としたとき、c_1,c_2,\ldots,c_N をこの順で空白区切りで出力せよ。
入力例 1
5 2 1 4 3 5
出力例 1
3 2 2 1 0
i=1 について、条件を満たす j は 2,3,5 の 3 つです。(ビル 1 とビル 4 の間にはビル 4 より高いビル 3 が存在するため、j=4 は条件を満たしません。)よって、出力の 1 つ目は 3 になります。
入力例 2
4 1 2 3 4
出力例 2
3 2 1 0
入力例 3
10 1 9 6 5 2 7 10 4 8 3
出力例 3
2 3 3 3 2 1 2 1 1 0
Score : 400 points
Problem Statement
There are N buildings, Building 1, Building 2, \ldots, Building N, arranged in a line in this order. The height of Building i (1 \leq i \leq N) is H_i.
For each i = 1, 2, \ldots, N, find the number of integers j (i < j \leq N) satisfying the following condition:
- There is no building taller than Building j between Buildings i and j.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq H_i \leq N
- H_i\neq H_j\ (i\neq j)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N H_1 H_2 \ldots H_N
Output
For each i = 1, 2, \ldots, N, let c_i be the number of j satisfying the condition. Print c_1, c_2, \ldots, c_N in order, separated by spaces.
Sample Input 1
5 2 1 4 3 5
Sample Output 1
3 2 2 1 0
For i=1, the integers j satisfying the condition are 2, 3, and 5: there are three. (Between Buildings 1 and 4, there is a building taller than Building 4, which is Building 3, so j=4 does not satisfy the condition.) Therefore, the first number in the output is 3.
Sample Input 2
4 1 2 3 4
Sample Output 2
3 2 1 0
Sample Input 3
10 1 9 6 5 2 7 10 4 8 3
Sample Output 3
2 3 3 3 2 1 2 1 1 0
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 475 点
問題文
以下の条件を満たす k+1 頂点 k 辺のグラフをレベル k\ (k\geq 2) の星と呼びます。
- ある 1 つの頂点が、他の k 個の頂点と 1 本ずつ辺で結ばれている。それ以外の辺は存在しない。
高橋君は、はじめ何個かの星からなるグラフを持っていました。そして、以下の手続きを全てのグラフの頂点が連結になるまでくり返し行いました。
- 持っているグラフの頂点から二つの頂点を選ぶ。このとき、選んだ二つの頂点の次数は共に 1 であり、かつ選んだ二つの頂点は非連結である必要がある。選んだ二つの頂点を結ぶ辺を張る。
その後、高橋君は手続きが終了した後のグラフの頂点に、適当に 1 から N の番号を付けました。このグラフは木となっており、これを T と呼びます。T には N-1 本の辺があり、 i 番目の辺は u_i と v_i を結んでいました。
その後高橋君は、はじめ持っていた星の個数とレベルを忘れてしまいました。T の情報からはじめ持っていた星の個数とレベルを求めてください。
制約
- 3\leq N\leq 2\times 10^5
- 1\leq u_i, v_i\leq N
- 与えられるグラフは、問題文中の手続きによって得られる N 頂点の木
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
u_1 v_1
\vdots
u_{N-1} v_{N-1}
出力
高橋君が持っていた星が M 個であり、星のレベルがそれぞれ L=(L_1,L_2,\ldots,L_M) であったとする。 このとき、L を昇順に並び替え空白区切りで出力せよ。
なお、この問題では常に解が一意に定まることが証明できる。
入力例 1
6 1 2 2 3 3 4 4 5 5 6
出力例 1
2 2
以下の図のように、2 つのレベル 2 の星から T は得られます。

入力例 2
9 3 9 7 8 8 6 4 6 4 1 5 9 7 3 5 2
出力例 2
2 2 2
入力例 3
20 8 3 8 18 2 19 8 20 9 17 19 7 8 7 14 12 2 15 14 10 2 13 2 16 2 1 9 5 10 15 14 6 2 4 2 11 5 12
出力例 3
2 3 4 7
Score : 475 points
Problem Statement
A graph with (k+1) vertices and k edges is called a level-k\ (k\geq 2) star if and only if:
- it has a vertex that is connected to each of the other k vertices with an edge, and there are no other edges.
At first, Takahashi had a graph consisting of stars. He repeated the following operation until every pair of vertices in the graph was connected:
- choose two vertices in the graph. Here, the vertices must be disconnected, and their degrees must be both 1. Add an edge that connects the chosen two vertices.
He then arbitrarily assigned an integer from 1 through N to each of the vertices in the graph after the procedure. The resulting graph is a tree; we call it T. T has (N-1) edges, the i-th of which connects u_i and v_i.
Takahashi has now forgotten the number and levels of the stars that he initially had. Find them, given T.
Constraints
- 3\leq N\leq 2\times 10^5
- 1\leq u_i, v_i\leq N
- The given graph is an N-vertex tree obtained by the procedure in the problem statement.
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N
u_1 v_1
\vdots
u_{N-1} v_{N-1}
Output
Suppose that Takahashi initially had M stars, whose levels were L=(L_1,L_2,\ldots,L_M). Sort L in ascending order, and print them with spaces in between.
We can prove that the solution is unique in this problem.
Sample Input 1
6 1 2 2 3 3 4 4 5 5 6
Sample Output 1
2 2
Two level-2 stars yield T, as the following figure shows:

Sample Input 2
9 3 9 7 8 8 6 4 6 4 1 5 9 7 3 5 2
Sample Output 2
2 2 2
Sample Input 3
20 8 3 8 18 2 19 8 20 9 17 19 7 8 7 14 12 2 15 14 10 2 13 2 16 2 1 9 5 10 15 14 6 2 4 2 11 5 12
Sample Output 3
2 3 4 7
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
カード 1, カード 2, \ldots, カード N の N 枚のカードがあり、 カード i (1\leq i\leq N) には整数 A_i が書かれています。
K=1,2,\ldots,N について、次の問題を解いてください。
カード 1, カード 2, \ldots, カード K の K 枚のカードが入っている袋があります。
次の操作を 2 回繰り返し、記録された数を順に x,y とします。袋から無作為にカードを 1 枚取り出し、カードに書かれている数を記録する。その後、カードを 袋の中に戻す 。
\max(x,y) の値の期待値を \text{mod} 998244353 で出力してください(注記参照)。
ただし、\max(x,y) で x と y のうち小さくない方の値を表します。
注記
求める期待値は必ず有限値かつ有理数となることが証明できます。また、この問題の制約下では、その値を互いに素な 2 つの整数 P, Q を用いて \frac{P}{Q} と表したとき、R \times Q \equiv P\pmod{998244353} かつ 0 \leq R \lt 998244353 を満たす整数 R がただ一つ存在することが証明できます。この R を出力してください。
制約
- 1 \leq N \leq 2\times 10^5
- 1 \leq A_i \leq 2\times 10^5
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
N 行出力せよ。 i 行目 (1\leq i\leq N) には、K=i の時の問題に対する答えを出力せよ。
入力例 1
3 5 7 5
出力例 1
5 499122183 443664163
例えば、K=2 の時の答えは次のようにして求まります。
袋の中にはカード 1 とカード 2 が入っており、それぞれには A_1=5 と A_2=7 が書かれています。
- 1 回目に取り出されたカードがカード 1 、2 回目に取り出されたカードもカード 1 のとき、x=y=5 であり、\max(x,y)=5 となります。
- 1 回目に取り出されたカードがカード 1 、2 回目に取り出されたカードはカード 2 のとき、x=5, y=7 であり、\max(x,y)=7 となります。
- 1 回目に取り出されたカードがカード 2 、2 回目に取り出されたカードはカード 1 のとき、x=7, y=5 であり、\max(x,y)=7 となります。
- 1 回目に取り出されたカードがカード 2 、2 回目に取り出されたカードもカード 2 のとき、x=y=7 であり、\max(x,y)=7 となります。
これらが等確率で起こるため、期待値は \frac{5+7+7+7}{4}=\frac{13}{2} となります。 499122183\times 2\equiv 13 \pmod{998244353} であるため、499122183 を出力します。
入力例 2
7 22 75 26 45 72 81 47
出力例 2
22 249561150 110916092 873463862 279508479 360477194 529680742
Score : 500 points
Problem Statement
There are N cards called card 1, card 2, \ldots, card N. On card i (1\leq i\leq N), an integer A_i is written.
For K=1, 2, \ldots, N, solve the following problem.
We have a bag that contains K cards: card 1, card 2, \ldots, card K.
Let us perform the following operation twice, and let x and y be the numbers recorded, in the recorded order.Draw a card from the bag uniformly at random, and record the number written on that card. Then, return the card to the bag.
Print the expected value of \max(x,y), modulo 998244353 (see Notes).
Here, \max(x,y) denotes the value of the greater of x and y (or x if they are equal).
Notes
It can be proved that the sought expected value is always finite and rational. Additionally, under the Constraints of this problem, when that value is represented as \frac{P}{Q} with two coprime integers P and Q, it can be proved that there is a unique integer R such that R \times Q \equiv P\pmod{998244353} and 0 \leq R \lt 998244353. Print this R.
Constraints
- 1 \leq N \leq 2\times 10^5
- 1 \leq A_i \leq 2\times 10^5
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Print N lines. The i-th line (1\leq i\leq N) should contain the answer to the problem for K=i.
Sample Input 1
3 5 7 5
Sample Output 1
5 499122183 443664163
For instance, the answer for K=2 is found as follows.
The bag contains card 1 and card 2, with A_1=5 and A_2=7 written on them, respectively.
- If you draw card 1 in the first draw and card 1 again in the second draw, we have x=y=5, so \max(x,y)=5.
- If you draw card 1 in the first draw and card 2 in the second draw, we have x=5 and y=7, so \max(x,y)=7.
- If you draw card 2 in the first draw and card 1 in the second draw, we have x=7 and y=5, so \max(x,y)=7.
- If you draw card 2 in the first draw and card 2 again in the second draw, we have x=y=7, so \max(x,y)=7.
These events happen with the same probability, so the sought expected value is \frac{5+7+7+7}{4}=\frac{13}{2}. We have 499122183\times 2\equiv 13 \pmod{998244353}, so 499122183 should be printed.
Sample Input 2
7 22 75 26 45 72 81 47
Sample Output 2
22 249561150 110916092 873463862 279508479 360477194 529680742