実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
高橋くんは、頭パーツを 1 個と体パーツを 1 個組み合わせてロボットを 1 体作ることができます。 ロボットは頭パーツの重さが体パーツの重さより大きいと倒れてしまいます。
現在、高橋くんは頭パーツと体パーツを 1 個ずつ持っています。 高橋くんが持っている頭パーツの重さは H グラム、体パーツの重さは B グラムです。
高橋くんは、体パーツを重くすることで、ロボットを倒れないようにしたいです。 高橋くんが作るロボットが倒れないようにするためには、体パーツをあと何グラム重くする必要があるか求めてください。
制約
- 1\le H\le100
- 1\le B\le100
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H B
出力
答えを出力せよ。
入力例 1
43 1
出力例 1
42
高橋くんは、体パーツを 42 グラム重くすることで、頭パーツと体パーツの重さを等しくすることができます。
体パーツを重くする量が 42 グラム未満のとき、高橋くんが作るロボットは倒れてしまうため、42 を出力してください。
入力例 2
4 31
出力例 2
0
高橋くんがこのままロボットを作ってもロボットは倒れないため、0 を出力してください。
入力例 3
1 1
出力例 3
0
Score : 100 points
Problem Statement
Takahashi can combine a head part and a body part to create a robot. A robot falls over if the weight of the head part is greater than the weight of the body part.
Currently, he has one head part and one body part. The weight of the head part is H grams, and the weight of the body part is B grams.
He wants to make the body part heavier so that the robot does not fall over. Find how many more grams the body part needs to be made heavier so that his robot does not fall over.
Constraints
- 1\le H\le100
- 1\le B\le100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H B
Output
Print the answer.
Sample Input 1
43 1
Sample Output 1
42
By making the body part 42 grams heavier, Takahashi can make the weights of the head part and body part equal.
When the amount by which the body part is made heavier is less than 42 grams, his robot will fall over, so print 42.
Sample Input 2
4 31
Sample Output 2
0
Even if he creates the robot as is, the robot will not fall over, so print 0.
Sample Input 3
1 1
Sample Output 3
0
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
ロボットがあり、はじめロボットの重さは X です。 このロボットには、同時に取り付けられる部品が種類 1, 種類 2,\ldots, 種類 N の N 種類あります。 種類 i\ (1\le i\le N) の部品の重さは W _ i です。 はじめ、ロボットには N 種類のうちのどの部品もついていません。
次の Q 個のクエリを順に処理してください。 i 番目 (1\le i\le Q) のクエリは、整数 P _ i で表される次のようなクエリです。
- 現在、ロボットに種類 P _ i の部品がついていない場合は取り付け、ついている場合は取り外す。その後、現在のロボットの重さを出力する。
制約
- 1\le X\le100
- 1\le N\le100
- 1\le W _ i\le100\ (1\le i\le N)
- 1\le Q\le100
- 1\le P _ i\le N\ (1\le i\le Q)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
X N W _ 1 W _ 2 \ldots W _ N Q P _ 1 P _ 2 \vdots P _ Q
出力
Q 行にわたって出力せよ。 i 行目 (1\le i\le Q) には、i 番目のクエリを処理した結果を出力せよ。
入力例 1
31 4 15 92 65 35 4 3 1 4 1
出力例 1
96 111 146 131
はじめ、ロボットの重さは 31 です。 それぞれのクエリで、ロボットの重さは次のようになります。
- 1 番目のクエリでは、種類 3 のパーツをロボットに取り付ける。ロボットの重さは 31+65=96 になる。
- 2 番目のクエリでは、種類 1 のパーツをロボットに取り付ける。ロボットの重さは 96+15=111 になる。
- 3 番目のクエリでは、種類 4 のパーツをロボットに取り付ける。ロボットの重さは 111+35=146 になる。
- 4 番目のクエリでは、種類 1 のパーツをロボットから取り外す。ロボットの重さは 146-15=131 になる。
入力例 2
41 10 73 8 55 26 97 48 37 47 35 55 15 1 2 7 1 6 3 10 8 4 8 1 5 9 9 3
出力例 2
114 122 159 86 134 189 244 291 317 270 343 440 475 440 385
Score : 200 points
Problem Statement
There is a robot, and initially the weight of the robot is X. This robot has N types of parts that can be attached simultaneously: type 1, type 2,\ldots, type N. The weight of the type i\ (1\le i\le N) part is W _ i. Initially, none of the N types of parts are attached to the robot.
Process the following Q queries in order. The i-th query (1\le i\le Q) is represented by an integer P _ i and is as follows:
- If the type P _ i part is not currently attached to the robot, attach it; if it is attached, remove it. Then, print the current weight of the robot.
Constraints
- 1\le X\le100
- 1\le N\le100
- 1\le W _ i\le100\ (1\le i\le N)
- 1\le Q\le100
- 1\le P _ i\le N\ (1\le i\le Q)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
X N W _ 1 W _ 2 \ldots W _ N Q P _ 1 P _ 2 \vdots P _ Q
Output
Output Q lines. The i-th line (1\le i\le Q) should contain the result of processing the i-th query.
Sample Input 1
31 4 15 92 65 35 4 3 1 4 1
Sample Output 1
96 111 146 131
Initially, the weight of the robot is 31. For each query, the weight of the robot becomes as follows:
- In the 1-st query, attach the type 3 part to the robot. The weight of the robot becomes 31+65=96.
- In the 2-nd query, attach the type 1 part to the robot. The weight of the robot becomes 96+15=111.
- In the 3-rd query, attach the type 4 part to the robot. The weight of the robot becomes 111+35=146.
- In the 4-th query, remove the type 1 part from the robot. The weight of the robot becomes 146-15=131.
Sample Input 2
41 10 73 8 55 26 97 48 37 47 35 55 15 1 2 7 1 6 3 10 8 4 8 1 5 9 9 3
Sample Output 2
114 122 159 86 134 189 244 291 317 270 343 440 475 440 385
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
高橋くんは、頭パーツを 1 個と体パーツを 1 個組み合わせてロボットを 1 体作ることができます。 ロボットは頭パーツの重さが体パーツの重さより大きいと倒れてしまいます。
現在、高橋くんは頭パーツを N 個と体パーツを M 個持っています。 高橋くんが持っている i 番目 (1\le i\le N) の頭パーツの重さは H _ i グラム、i 番目 (1\le i\le M) の体パーツの重さは B _ i グラムです。
高橋くんは、持っているパーツを適切に組み合わせることで、倒れないロボットを合計 K 体作りたいです。 うまくパーツを組み合わせることで高橋くんが目標を達成することができるか判定してください。
ただし、1 個のパーツを複数のロボットを作るために利用したり、1 体のロボットを作るために頭パーツを 2 個以上(もしくは体パーツを 2 個以上)利用することはできません。
制約
- 1\le N\le2\times10 ^ 5
- 1\le M\le2\times10 ^ 5
- 1\le K\le\min\lbrace N,M\rbrace
- 1\le H _ i\le10 ^ 9\ (1\le i\le N)
- 1\le B _ i\le10 ^ 9\ (1\le i\le M)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M K H _ 1 H _ 2 \ldots H _ N B _ 1 B _ 2 \ldots B _ M
出力
高橋くんがパーツをうまく組み合わせて倒れないロボットを K 体作ることができるなら Yes を、そうでなければ No を出力せよ。
入力例 1
6 6 3 2 7 1 8 2 8 1 8 2 8 4 5
出力例 1
Yes
i 番目の頭パーツと j 番目の体パーツを組み合わせることを (i,j) と書くことにすると、高橋くんは例えば (1,2),(2,4),(3,6) のように組み合わせることで 3 体の倒れないロボットを作ることができます。
よって、Yes を出力してください。
入力例 2
1 1 1 43 1
出力例 2
No
高橋くんが持っている頭パーツが重すぎるため、高橋くんは倒れないロボットを作ることができません。
入力例 3
1 1 1 100 100
出力例 3
Yes
頭の重さと体の重さが等しい場合、ロボットは倒れないことに注意してください。
入力例 4
12 15 12 748 169 586 329 972 529 432 519 408 587 138 249 656 114 632 299 984 755 404 772 155 506 832 854 353 465 387
出力例 4
Yes
Score : 300 points
Problem Statement
Takahashi can combine a head part and a body part to create a robot. A robot falls over if the weight of the head part is greater than the weight of the body part.
Currently, he has N head parts and M body parts. The weight of the i-th (1\le i\le N) head part is H _ i grams, and the weight of the i-th (1\le i\le M) body part is B _ i grams.
He wants to create a total of K robots that do not fall over by appropriately combining the parts he has. Determine whether he can achieve his goal by combining the parts well.
Here, a part cannot be used to create multiple robots, and two or more head parts (or two or more body parts) cannot be used to create one robot.
Constraints
- 1\le N\le2\times10 ^ 5
- 1\le M\le2\times10 ^ 5
- 1\le K\le\min\lbrace N,M\rbrace
- 1\le H _ i\le10 ^ 9\ (1\le i\le N)
- 1\le B _ i\le10 ^ 9\ (1\le i\le M)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M K H _ 1 H _ 2 \ldots H _ N B _ 1 B _ 2 \ldots B _ M
Output
Print Yes if Takahashi can combine the parts well to create K robots that do not fall over; otherwise, print No.
Sample Input 1
6 6 3 2 7 1 8 2 8 1 8 2 8 4 5
Sample Output 1
Yes
If we denote combining the i-th head part and the j-th body part as (i,j), then Takahashi can create three robots that do not fall over by combining them as (1,2),(2,4),(3,6), for example.
Thus, print Yes.
Sample Input 2
1 1 1 43 1
Sample Output 2
No
His head part is too heavy, so he cannot create any robot that does not fall over.
Sample Input 3
1 1 1 100 100
Sample Output 3
Yes
Note that a robot does not fall over if the head and body have equal weights.
Sample Input 4
12 15 12 748 169 586 329 972 529 432 519 408 587 138 249 656 114 632 299 984 755 404 772 155 506 832 854 353 465 387
Sample Output 4
Yes
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
頭と体からなるロボットがあります。 このロボットには、同時に取り付けられる部品が種類 1, 種類 2,\ldots, 種類 N の N 種類あります。 種類 i\ (1\le i\le N) の部品の重さは W _ i です。 それぞれの部品には、頭に取り付けたときと体に取り付けたときで異なる嬉しさがあります。 種類 i\ (1\le i\le N) の部品を頭に取り付けたときの嬉しさは H _ i 、体に取り付けたときの嬉しさは B _ i です。
ロボットは頭の重さが体の重さより大きいと倒れてしまいます。 ここで、頭の重さおよび体の重さはそれぞれ頭もしくは体に取り付けられた部品の重さの合計とします。
高橋くんは、N 種類の部品をすべて 1 個ずつロボットに取り付けたいと思っています。 ロボットを倒さないように部品を取り付けたときの、すべての部品の嬉しさの合計としてありえる最大値を求めてください。
制約
- 1\le N\le500
- 1\le W _ i\le500\ (1\le i\le N)
- 1\le H _ i\le10 ^ 9\ (1\le i\le N)
- 1\le B _ i\le10 ^ 9\ (1\le i\le N)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N W _ 1 H _ 1 B _ 1 W _ 2 H _ 2 B _ 2 \vdots W _ N H _ N B _ N
出力
ロボットを倒さないように部品を取り付けたときの、すべての部品の嬉しさの合計としてありえる最大値を出力せよ。
入力例 1
3 1 41 59 2 65 35 8 97 93
出力例 1
217
種類 1 と種類 3 の部品を体に、種類 2 の部品を頭に取り付けることで、ロボットを倒さないようにしつつ嬉しさの合計を 217 にすることができます。
ロボットを倒さないように部品を取り付けて嬉しさの合計を 218 以上にすることはできないため、217 を出力してください。
入力例 2
1 1 1000000000 1
出力例 2
1
唯一の部品を体に取り付けないとロボットは倒れてしまいます。 頭にひとつも部品を取り付けなくてもよいことに注意してください。
入力例 3
2 1 1000000000 1 1 1 1000000000
出力例 3
2000000000
頭の重さと体の重さが等しい場合、ロボットは倒れないことに注意してください。
入力例 4
20 483 984529882 299667119 372 428935469 104847758 467 709733529 102461200 421 659244277 110859936 231 786224280 773073478 351 334234040 193222121 119 404159408 772024933 302 519596088 432627257 433 910226244 337833733 184 406236461 530198622 335 465203041 353047747 418 656273464 114923636 482 972364803 329650748 453 748321854 169441643 105 138464898 587159653 401 832952051 506021805 403 810916971 468755944 231 798801044 749313343 292 631278033 556088607 366 567211596 374825770
出力例 4
12091388792
答えが 2 ^ {32} を超える場合があることに注意してください。
Score : 400 points
Problem Statement
There is a robot consisting of a head and a body. This robot has N types of parts that can be attached simultaneously: type 1, type 2,\ldots, type N. The weight of the type i\ (1\le i\le N) part is W _ i. Each part has a different happiness when attached to the head versus when attached to the body. The happiness when the type i\ (1\le i\le N) part is attached to the head is H _ i, and the happiness when attached to the body is B _ i.
The robot falls over if the weight of the head is greater than the weight of the body. Here, the weight of the head and the weight of the body are the sums of the weights of the parts attached to the head or body, respectively.
Takahashi wants to attach all N types of parts to the robot, one of each. Find the maximum possible sum of the happiness of all parts when the parts are attached without causing the robot to fall over.
Constraints
- 1\le N\le500
- 1\le W _ i\le500\ (1\le i\le N)
- 1\le H _ i\le10 ^ 9\ (1\le i\le N)
- 1\le B _ i\le10 ^ 9\ (1\le i\le N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N W _ 1 H _ 1 B _ 1 W _ 2 H _ 2 B _ 2 \vdots W _ N H _ N B _ N
Output
Print the maximum possible sum of the happiness of all parts when the parts are attached without causing the robot to fall over.
Sample Input 1
3 1 41 59 2 65 35 8 97 93
Sample Output 1
217
By attaching type 1 and type 3 parts to the body and type 2 part to the head, the robot does not fall over and the sum of happiness can be made 217.
It is not possible to attach the parts without causing the robot to fall over and make the sum of happiness 218 or more, so print 217.
Sample Input 2
1 1 1000000000 1
Sample Output 2
1
The robot will fall over if the only part is not attached to the body. Note that it is acceptable to attach no parts to the head.
Sample Input 3
2 1 1000000000 1 1 1 1000000000
Sample Output 3
2000000000
Note that the robot does not fall over if the head and body have equal weights.
Sample Input 4
20 483 984529882 299667119 372 428935469 104847758 467 709733529 102461200 421 659244277 110859936 231 786224280 773073478 351 334234040 193222121 119 404159408 772024933 302 519596088 432627257 433 910226244 337833733 184 406236461 530198622 335 465203041 353047747 418 656273464 114923636 482 972364803 329650748 453 748321854 169441643 105 138464898 587159653 401 832952051 506021805 403 810916971 468755944 231 798801044 749313343 292 631278033 556088607 366 567211596 374825770
Sample Output 4
12091388792
Note that the answer can exceed 2 ^ {32}.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : {500} 点
問題文
H 行 W 列のマス目があります。 上から i 行目、左から j 列目のマスをマス (i,j) と呼ぶことにします。各マスには鏡が高々 1 枚置いてあります。
高橋君はマス (1,1) の左側、青木くんはマス (H,W) の右側に立っています。高橋君は懐中電灯を持っており、マス (1,1) の左側から右に向かって光を入れています。ここで、懐中電灯の光は拡散せず、まっすぐに進む光線であるとします。
高橋君の目標は、マス目にある鏡を利用して懐中電灯の光を青木君に届けることです。
鏡の置き方は次の 3 種類あります。光が鏡に当たると、鏡の置き方に応じて光の進む向きが変わります。それぞれの鏡の置き方について、光が入る方向に対する出る方向は下図のようになります。
- タイプ A (鏡は置かれていない)
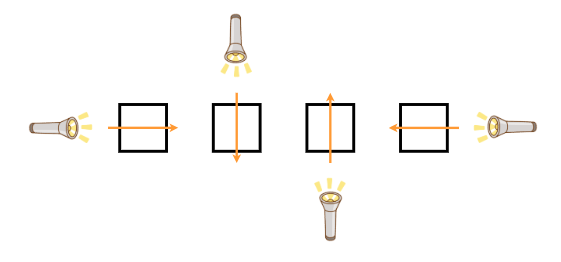
- タイプ B (左上と右下を結ぶ対角線上に鏡が置かれている)
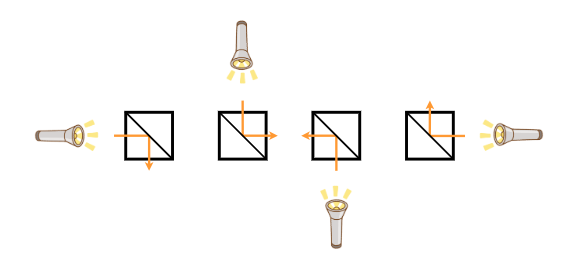
- タイプ C (右上と左下を結ぶ対角線上に鏡が置かれている)
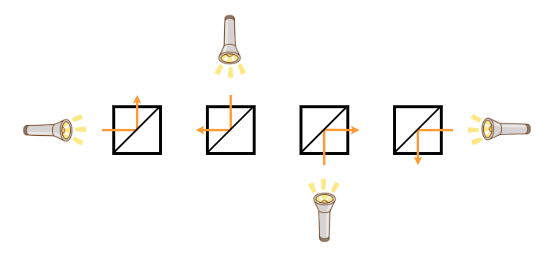
マス目の鏡の置き方は H 個の長さ W の文字列 S_1,S_2,\ldots,S_H で表されます。S_i の j 文字目が A のときマス (i,j) はタイプ A、B のときマス (i,j) はタイプ B、C のときマス (i,j) はタイプ C です。
高橋君は、青木君に光を届けるために以下の操作を好きな回数行うことができます。
- あるマスを 1 つ選び、そのマスの鏡の置き方を別のタイプに変更する
青木君に光を届けるためには最低何回操作を行う必要があるか求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1\leq T
- 1\leq H,W
- HW\leq 2\times 10^5
- S_i は
A,B,Cからなる長さ W の文字列 - T,H,W は整数
- 全てのテストケースに対する HW の総和は 2\times 10^5 以下
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
各テストケースは以下の形式で与えられる。
H W S_1 S_2 \vdots S_H
出力
T 行出力せよ。i 行目には i 番目のテストケースに対する答えを出力せよ。
入力例 1
4 3 4 ABCB CACC BCBA 2 2 CB AA 1 10 BCBCBCBCBC 10 10 CCAABACAAA CCCBACACCA BACAABCBBA ACCCAACCCA CCAAAACCBA AACBBACCAA BCCCACBBAB CBBCAACCCC CBBCCBCBCA BBACABBACC
出力例 1
0 2 10 5
1 つ目のテストケースについて、操作を行わなくても青木君に光を届けることができます。
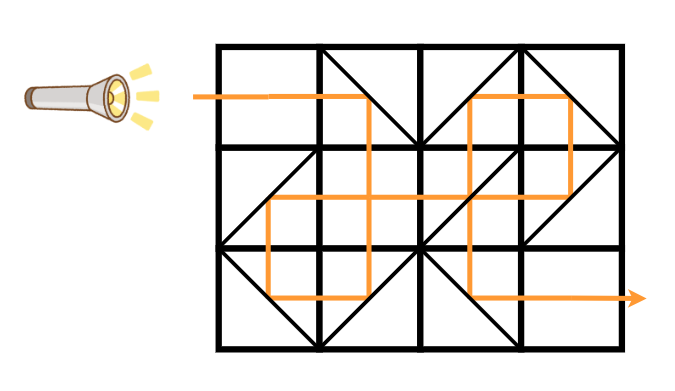
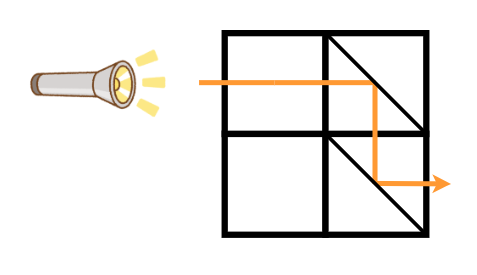
2 つ目のテストケースについて、マス (1,1) の鏡の置き方をタイプ A に、マス (2,2) の鏡の置き方をタイプ B に変更することで、下図のように青木君に光を届けることができます。1 回以下の操作で青木君に光を届けることはできないので、答えは 2 です。
Score : 500 points
Problem Statement
There is a grid with H rows and W columns. We will refer to the cell at the i-th row from the top and j-th column from the left as cell (i,j). Each cell has at most one mirror placed on it.
Takahashi is standing on the left side of cell (1,1), and Aoki is standing on the right side of cell (H,W). Takahashi has a flashlight and is shining light from the left side of cell (1,1) toward the right. Here, assume that the flashlight's light does not diffuse and is a light ray that travels straight.
Takahashi's goal is to deliver the flashlight's light to Aoki by using the mirrors in the grid.
There are three types of mirror placements. When light hits a mirror, the direction of the light changes according to the mirror placement. For each mirror placement, the exit direction for each entry direction is as shown in the figures below.
- Type A (no mirror is placed)
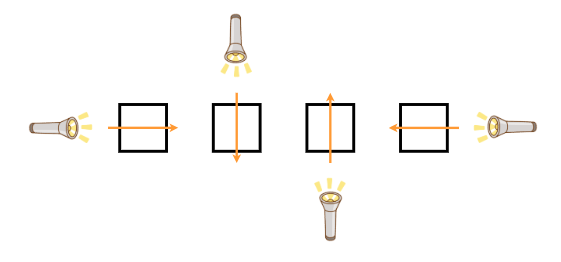
- Type B (a mirror is placed on the diagonal connecting the upper-left and lower-right)

- Type C (a mirror is placed on the diagonal connecting the upper-right and lower-left)

The mirror placement on the grid is represented by H strings of length W: S_1,S_2,\ldots,S_H. When the j-th character of S_i is A, cell (i,j) is type A; when it is B, cell (i,j) is type B; when it is C, cell (i,j) is type C.
Takahashi can perform the following operation any number of times to deliver the light to Aoki:
- Choose one cell and change the mirror placement of that cell to a different type.
Find the minimum number of operations needed to deliver the light to Aoki.
You are given T test cases; find the answer for each.
Constraints
- 1\leq T
- 1\leq H,W
- HW\leq 2\times 10^5
- S_i is a string of length W consisting of
A,B,C. - T, H, and W are integers.
- The sum of HW over all test cases is at most 2\times 10^5.
Input
The input is given from Standard Input in the following format:
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
Each test case is given in the following format:
H W S_1 S_2 \vdots S_H
Output
Output T lines. The i-th line should contain the answer for the i-th test case.
Sample Input 1
4 3 4 ABCB CACC BCBA 2 2 CB AA 1 10 BCBCBCBCBC 10 10 CCAABACAAA CCCBACACCA BACAABCBBA ACCCAACCCA CCAAAACCBA AACBBACCAA BCCCACBBAB CBBCAACCCC CBBCCBCBCA BBACABBACC
Sample Output 1
0 2 10 5
For the first test case, the light can be delivered to Aoki without performing any operations.

For the second test case, by changing the mirror placement of cell (1,1) to type A and the mirror placement of cell (2,2) to type B, the light can be delivered to Aoki as shown in the figure below. It is impossible to deliver the light to Aoki with one or fewer operations, so the answer is 2.

実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : {500} 点
問題文
長さ N の整数列 A=(A_1,A_2,\ldots,A_N) および正整数 D が与えられます。
A を並び替えることで得られる整数列 B=(B_1, B_2, \ldots, B_N) であって、次の条件を満たすものの個数を 998244353 で割ったあまりを求めてください。
- すべての i\ (1\leq i\leq N-1) に対して B_{i+1}\geq B_i-D が成り立つ。
制約
- 2\leq N\leq 2\times 10^5
- 1\leq D\leq 10^6
- 1\leq A_i\leq 10^6
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N D A_1 A_2 \ldots A_N
出力
答えを出力せよ。
入力例 1
4 1 5 2 1 2
出力例 1
3
条件を満たす整数列は (1,2,2,5),(2,1,2,5),(2,2,1,5) の 3 つです。
入力例 2
5 10 20 40 60 80 100
出力例 2
1
入力例 3
15 12345 18270 31252 27543 31406 22271 13402 12279 25697 18349 27615 39360 22790 32581 23990 36154
出力例 3
858152905
Score : 500 points
Problem Statement
You are given an integer sequence A=(A_1,A_2,\ldots,A_N) of length N and a positive integer D.
Find the number, modulo 998244353, of integer sequences B=(B_1, B_2, \ldots, B_N) that can be obtained by rearranging A and satisfy the following condition:
- B_{i+1}\geq B_i-D holds for all i\ (1\leq i\leq N-1).
Constraints
- 2\leq N\leq 2\times 10^5
- 1\leq D\leq 10^6
- 1\leq A_i\leq 10^6
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N D A_1 A_2 \ldots A_N
Output
Print the answer.
Sample Input 1
4 1 5 2 1 2
Sample Output 1
3
The integer sequences satisfying the condition are (1,2,2,5),(2,1,2,5),(2,2,1,5), which are three sequences.
Sample Input 2
5 10 20 40 60 80 100
Sample Output 2
1
Sample Input 3
15 12345 18270 31252 27543 31406 22271 13402 12279 25697 18349 27615 39360 22790 32581 23990 36154
Sample Output 3
858152905
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : {575} 点
問題文
長さ N の整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
整数の組 (l, r) \ (1\leq l\lt r\leq N) に対し、f(l,r) を「A の l 番目の要素と r 番目の要素を入れ替えることで得られる整数列」とします。
長さ \frac{N(N-1)}{2} の整数列の列 B=(B_1,B_2,\ldots,B_{\frac{N(N-1)}{2}}) を次の手順で生成します。
- 空の列 B=() を用意する。
- 各整数の組 (l, r)\ (1\leq l\lt r\leq N) に対し、B に f(l,r) を追加する。
- B を数列の辞書順でソートする。
Q 個のクエリが与えられるので、順に処理してください。i 番目のクエリは以下の通りです。
- 整数 k が与えられる。B_k=f(l,r) となるような整数の組 (l, r) \ (1\leq l\lt r\leq N) を一つ求めそれを出力せよ。
数列の辞書順とは?
数列 S = (S_1,S_2,\ldots,S_{|S|}) が数列 T = (T_1,T_2,\ldots,T_{|T|}) より辞書順で小さいとは、下記の 1. と 2. のどちらかが成り立つことを言います。 ここで、|S|, |T| はそれぞれ S, T の長さを表します。
- |S| \lt |T| かつ (S_1,S_2,\ldots,S_{|S|}) = (T_1,T_2,\ldots,T_{|S|})。
- ある整数 1 \leq i \leq \min\lbrace |S|, |T| \rbrace が存在して、下記の 2 つがともに成り立つ。
- (S_1,S_2,\ldots,S_{i-1}) = (T_1,T_2,\ldots,T_{i-1})
- S_i が T_i より(数として)小さい。
制約
- 2\leq N\leq 2\times 10^5
- 1\leq Q\leq 2\times 10^5
- 1\leq A_i\leq N
- 1\leq k\leq \frac{N(N-1)}{2}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q
A_1 A_2 \ldots A_N
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
各クエリは以下の形式で与えられる。
k
出力
Q 行出力せよ。i 行目には、i 番目のクエリに対する答えを以下の形式で出力せよ。
l r
答えが複数存在する場合、どれを出力しても正解とみなされる。
入力例 1
4 3 1 2 1 2 1 3 5
出力例 1
2 3 2 4 1 2
f(1, 2) = (2, 1, 1, 2), f(1, 3) = (1, 2, 1, 2), f(1, 4) = (2, 2, 1, 1), f(2, 3) = (1, 1, 2, 2), f(2, 4) = (1, 2, 1, 2), f(3, 4) = (1, 2, 2, 1) です。
これら 6 つの数列を辞書順でソートした列 B は B=((1, 1, 2, 2), (1, 2, 1, 2), (1, 2, 1, 2), (1, 2, 2, 1), (2, 1, 1, 2), (2, 2, 1, 1)) です。
- 1 番目のクエリについて、B_1=(1,1,2,2)=f(l,r) が成り立つような (l,r) は (l,r)=(2,3) のみです。
- 2 番目のクエリについて、B_3=(1,2,1,2)=f(l,r) が成り立つような (l,r) は (l,r)=(1,3),(2,4) です。この場合、どちらを出力しても正解とみなされます。
- 3 番目のクエリについて、B_5=(2,1,1,2)=f(l,r) が成り立つような (l,r) は (l,r)=(1,2) のみです。
入力例 2
10 10 1 1 2 7 6 3 5 7 3 3 21 36 9 17 13 24 7 45 33 1
出力例 2
6 8 2 4 5 7 9 10 8 9 3 9 5 9 1 8 2 10 4 10
Score : {575} points
Problem Statement
You are given an integer sequence A=(A_1,A_2,\ldots,A_N) of length N.
For a pair of integers (l, r) \ (1\leq l\lt r\leq N), let f(l,r) be the integer sequence obtained by swapping the l-th element and the r-th element of A.
Generate a sequence of integer sequences B=(B_1,B_2,\ldots,B_{\frac{N(N-1)}{2}}) of length \frac{N(N-1)}{2} by the following procedure:
- Prepare an empty sequence B=().
- For each pair of integers (l, r)\ (1\leq l\lt r\leq N), add f(l,r) to B.
- Sort B in lexicographical order of sequences.
You are given Q queries; process them in order. The i-th query is as follows:
- Given an integer k, find one pair of integers (l, r) \ (1\leq l\lt r\leq N) such that B_k=f(l,r) and output it.
What is lexicographical order of sequences?
A sequence S = (S_1,S_2,\ldots,S_{|S|}) is lexicographically smaller than a sequence T = (T_1,T_2,\ldots,T_{|T|}) if and only if one of the following two conditions holds. Here, |S| and |T| represent the lengths of S and T, respectively.
- |S| \lt |T| and (S_1,S_2,\ldots,S_{|S|}) = (T_1,T_2,\ldots,T_{|S|}).
- There exists an integer 1 \leq i \leq \min\lbrace |S|, |T| \rbrace such that both of the following hold:
- (S_1,S_2,\ldots,S_{i-1}) = (T_1,T_2,\ldots,T_{i-1})
- S_i is smaller than T_i (as a number).
Constraints
- 2\leq N\leq 2\times 10^5
- 1\leq Q\leq 2\times 10^5
- 1\leq A_i\leq N
- 1\leq k\leq \frac{N(N-1)}{2}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q
A_1 A_2 \ldots A_N
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
Each query is given in the following format:
k
Output
Output Q lines. The i-th line should contain the answer to the i-th query in the following format:
l r
If there are multiple solutions, any of them will be considered correct.
Sample Input 1
4 3 1 2 1 2 1 3 5
Sample Output 1
2 3 2 4 1 2
f(1, 2) = (2, 1, 1, 2), f(1, 3) = (1, 2, 1, 2), f(1, 4) = (2, 2, 1, 1), f(2, 3) = (1, 1, 2, 2), f(2, 4) = (1, 2, 1, 2), f(3, 4) = (1, 2, 2, 1).
The sequence B obtained by sorting these six sequences in lexicographical order is B=((1, 1, 2, 2), (1, 2, 1, 2), (1, 2, 1, 2), (1, 2, 2, 1), (2, 1, 1, 2), (2, 2, 1, 1)).
- For the 1-st query, the only (l,r) such that B_1=(1,1,2,2)=f(l,r) is (l,r)=(2,3).
- For the 2-nd query, (l,r) such that B_3=(1,2,1,2)=f(l,r) are (l,r)=(1,3),(2,4). In this case, either one will be considered correct.
- For the 3-rd query, the only (l,r) such that B_5=(2,1,1,2)=f(l,r) is (l,r)=(1,2).
Sample Input 2
10 10 1 1 2 7 6 3 5 7 3 3 21 36 9 17 13 24 7 45 33 1
Sample Output 2
6 8 2 4 5 7 9 10 8 9 3 9 5 9 1 8 2 10 4 10