Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
正整数 N が与えられます。
i=1,2,\ldots,N について (-1)^i \times i^3 を計算したときの、それら N 個の値の総和を求めてください。
すなわち、 \displaystyle \sum_{i=1}^N (-1)^i \times i^3 を求めてください。
制約
- N は 1 以上 10 以下の整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
\displaystyle \sum_{i=1}^N (-1)^i \times i^3 の値を出力せよ。
入力例 1
3
出力例 1
-20
- i=1 のとき: (-1)^i\times i^3=-1 です。
- i=2 のとき: (-1)^i\times i^3=8 です。
- i=3 のとき: (-1)^i\times i^3=-27 です。
したがって、 -1 + 8 - 27 = -20 を出力してください。
入力例 2
9
出力例 2
-425
入力例 3
10
出力例 3
575
Score : 100 points
Problem Statement
You are given a positive integer N.
For i=1,2,\ldots,N, calculate (-1)^i \times i^3, and find the sum of these N values.
That is, find \displaystyle \sum_{i=1}^N (-1)^i \times i^3.
Constraints
- N is an integer between 1 and 10, inclusive.
Input
The input is given from Standard Input in the following format:
N
Output
Output the value of \displaystyle \sum_{i=1}^N (-1)^i \times i^3.
Sample Input 1
3
Sample Output 1
-20
- When i=1: (-1)^i\times i^3=-1.
- When i=2: (-1)^i\times i^3=8.
- When i=3: (-1)^i\times i^3=-27.
Therefore, output -1 + 8 - 27 = -20.
Sample Input 2
9
Sample Output 2
-425
Sample Input 3
10
Sample Output 3
575
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
長さ N の整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。ここで、 A の各要素は -1 または 1 以上 N 以下の整数です。
以下の条件を全て満たす長さ N の整数列 P=(P_1,P_2,\ldots,P_N) が存在するか判定し、存在するならば一つ求めてください。
- P は (1,2,\ldots,N) を並び替えてできる整数列である。
- i=1,2,\ldots,N に対し、 A_i \neq -1 ならば P_i=A_i が成り立つ。
制約
- 1\le N\le 10
- A_i=-1 または 1\le A_i \le N
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
条件を全て満たす P が存在しない場合は No と出力せよ。
そうでない場合、条件を全て満たす P を以下の形式で出力せよ。
Yes P_1 P_2 \ldots P_N
条件を全て満たす P が複数存在する場合、どれを出力しても正答となる。
入力例 1
4 -1 -1 2 -1
出力例 1
Yes 3 1 2 4
P=(3,1,2,4) とすると条件を全て満たします。
このほかにも、 P=(1,3,2,4) や P=(4,3,2,1) なども条件を全て満たします。
入力例 2
5 -1 -1 1 -1 1
出力例 2
No
条件を全て満たす P は存在しません。
入力例 3
7 3 -1 4 -1 5 -1 2
出力例 3
Yes 3 7 4 1 5 6 2
Score : 200 points
Problem Statement
You are given an integer sequence A=(A_1,A_2,\ldots,A_N) of length N. Here, each element of A is either -1 or an integer between 1 and N, inclusive.
Determine whether there exists an integer sequence P=(P_1,P_2,\ldots,P_N) of length N that satisfies all of the following conditions, and if it exists, find one.
- P is a permutation of (1,2,\ldots,N).
- For i=1,2,\ldots,N, if A_i \neq -1, then P_i=A_i holds.
Constraints
- 1\le N\le 10
- A_i=-1 or 1\le A_i \le N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
If there is no P that satisfies all conditions, output No.
Otherwise, output P that satisfies all conditions in the following format:
Yes P_1 P_2 \ldots P_N
If there are multiple P that satisfy all conditions, any of them may be output.
Sample Input 1
4 -1 -1 2 -1
Sample Output 1
Yes 3 1 2 4
P=(3,1,2,4) satisfies all conditions.
Besides this, P=(1,3,2,4) or P=(4,3,2,1) also satisfies all conditions.
Sample Input 2
5 -1 -1 1 -1 1
Sample Output 2
No
There is no P that satisfies all conditions.
Sample Input 3
7 3 -1 4 -1 5 -1 2
Sample Output 3
Yes 3 7 4 1 5 6 2
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
長さ N の整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
Q 個のクエリが与えられるので順に処理してください。クエリは 2 種類あり、以下のいずれかの形式で与えられます。
1 c: A の先頭の要素を末尾に移動させる操作を c 回行う。2 l r: \displaystyle \sum_{i=l}^r A_i の値を出力する。
制約
- 1\le N\le 2\times 10^5
- 1\le Q\le 2\times 10^5
- 1\le A_i \le 10^9
- 1\le c\le N
- 1\le l\le r \le N
- 2 つ目の形式のクエリが 1 つ以上存在する
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q
A_1 A_2 \ldots A_N
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
各クエリ \text{query}_i は以下の 2 種類のいずれかの形式で与えられる。
1 c
2 l r
出力
問題文の指示に従って 2 つ目の形式のクエリへの答えを改行区切りで出力せよ。
入力例 1
4 3 3 1 4 5 2 1 3 1 1 2 2 3
出力例 1
8 9
各クエリは以下のように処理されます。
- 1 つ目のクエリ: A_1+A_2+A_3=3+1+4=8 なので 8 を出力します。
- 2 つ目のクエリ: A=(3,1,4,5) が A=(1,4,5,3) に変化します。
- 3 つ目のクエリ: A_2+A_3=4+5=9 なので 9 を出力します。
入力例 2
5 7 1 2 4 8 16 2 1 5 1 4 1 5 2 1 5 2 2 4 1 1 2 3 3
出力例 2
31 31 7 4
Score : 350 points
Problem Statement
You are given an integer sequence A=(A_1,A_2,\ldots,A_N) of length N.
Process Q queries in order. There are two types of queries, given in the following formats:
1 c: Perform the operation of moving the first element of A to the end c times.2 l r: Output the value of \displaystyle \sum_{i=l}^r A_i.
Constraints
- 1\le N\le 2\times 10^5
- 1\le Q\le 2\times 10^5
- 1\le A_i \le 10^9
- 1\le c\le N
- 1\le l\le r \le N
- At least one query of the second type exists.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q
A_1 A_2 \ldots A_N
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
Each query \text{query}_i is given in one of the following two formats:
1 c
2 l r
Output
Following the instructions in the problem statement, output the answers to the second type queries, separated by newlines.
Sample Input 1
4 3 3 1 4 5 2 1 3 1 1 2 2 3
Sample Output 1
8 9
Each query is processed as follows:
- First query: A_1+A_2+A_3=3+1+4=8, so output 8.
- Second query: A=(3,1,4,5) changes to A=(1,4,5,3).
- Third query: A_2+A_3=4+5=9, so output 9.
Sample Input 2
5 7 1 2 4 8 16 2 1 5 1 4 1 5 2 1 5 2 2 4 1 1 2 3 3
Sample Output 2
31 31 7 4
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
H 行 W 列のマス目があります。上から i 行目 (1\leq i\leq H)、左から j 列目 (1\leq j\leq W) のマスをマス (i,j) と呼ぶことにします。
はじめ、マス (i,j) は S_{i,j} が # のとき黒、. のとき白で塗られています。
以下の操作を 10^{100} 回行います。
- 白で塗られているマスであって、そのマスに辺で隣接するマスのうちちょうど 1 つが黒で塗られているようなマスの集合を T とする。T の各マスに対して、そのマスを黒で塗る。ただし、2 つのマス (i_1,j_1),(i_2,j_2) が辺で隣接するとは、 |i_1-i_2|+|j_1-j_2|=1 であることをいう。
すべての操作が終わったあとに黒く塗られているマスの個数を求めてください。
制約
- 2\leq H,W
- HW\leq 3\times 10^5
- H,W は整数
- S_{i,j} は
#または.
入力
入力は以下の形式で標準入力から与えられる。
H W
S_{1,1}S_{1,2}\ldots S_{1,W}
S_{2,1}S_{2,2}\ldots S_{2,W}
\vdots
S_{H,1}S_{H,2}\ldots S_{H,W}
出力
答えを出力せよ。
入力例 1
9 9 ......... ......... ......... ......... ....#.... ......... ......... ......... .........
出力例 1
57
操作によってマス目は以下のように変化します。(上の数字は操作回数を表しており、10 回目の操作後まで表示しています。)
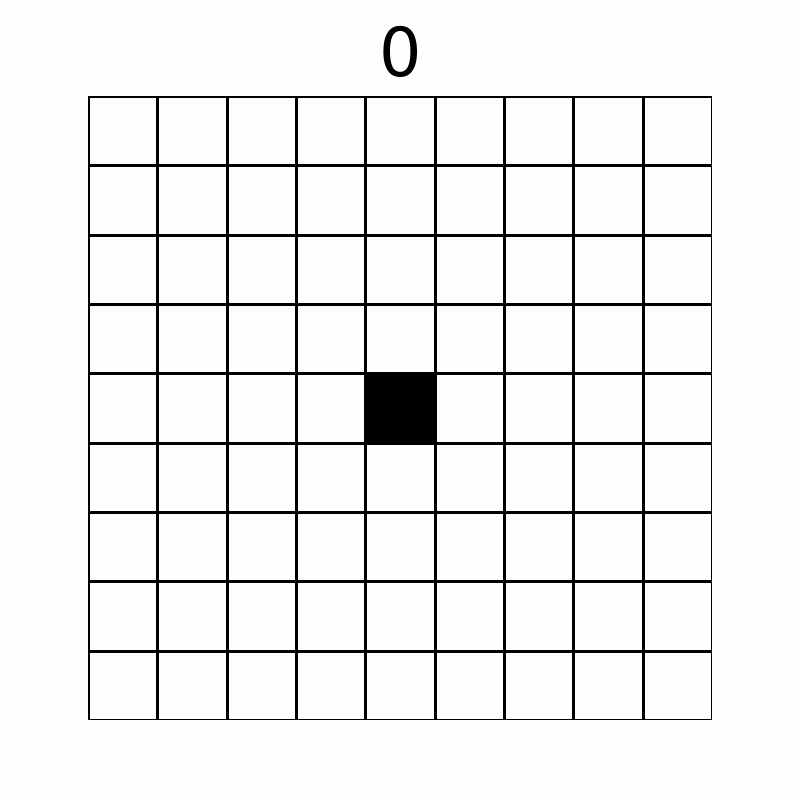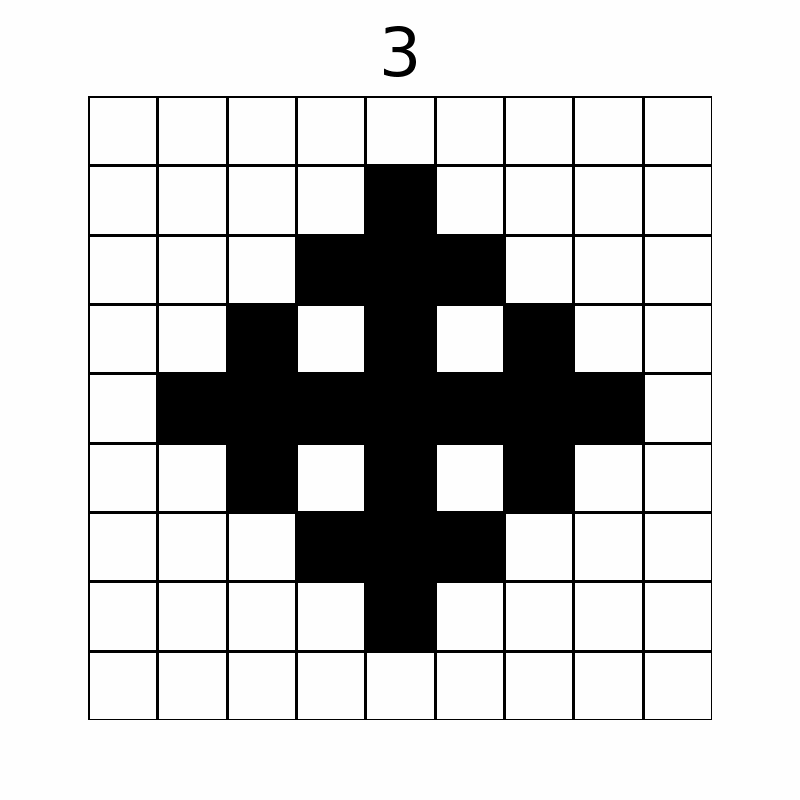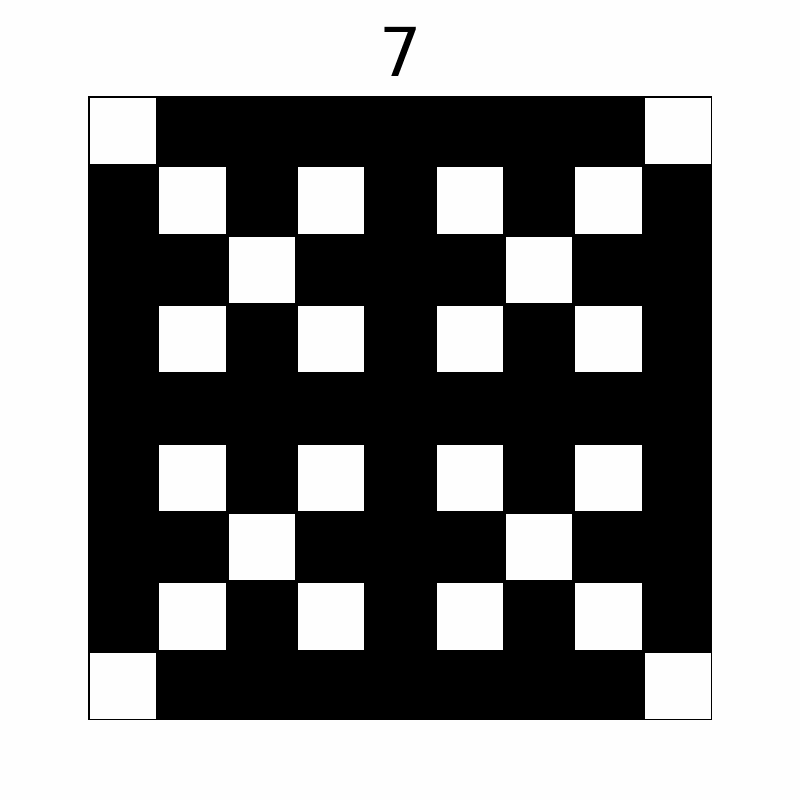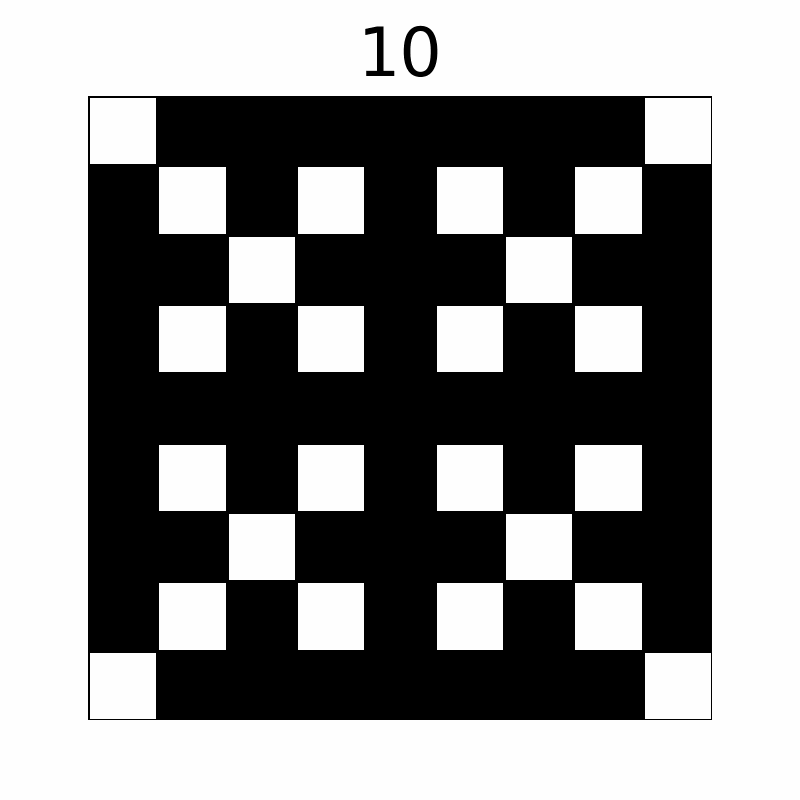
最終的に黒く塗られたマスは 57 個です。
入力例 2
2 2 .. ..
出力例 2
0
入力例 3
10 10 .......... ....#..... #.......#. ......#... .......#.. .....#.... .......... .......... ..#...#... .......#..
出力例 3
64
Score : 425 points
Problem Statement
There is a grid with H rows and W columns. We call the cell at the i-th row from the top (1\leq i\leq H) and j-th column from the left (1\leq j\leq W) as cell (i,j).
Initially, cell (i,j) is colored black if S_{i,j} is # and white if it is ..
Perform the following operation 10^{100} times:
- Let T be the set of cells that are colored white and have exactly one adjacent cell colored black. Color each cell in T black. Here, two cells (i_1,j_1) and (i_2,j_2) are adjacent if and only if |i_1-i_2|+|j_1-j_2|=1.
Find the number of cells that are colored black after all operations are completed.
Constraints
- 2\leq H,W
- HW\leq 3\times 10^5
- H and W are integers.
- S_{i,j} is
#or..
Input
The input is given from Standard Input in the following format:
H W
S_{1,1}S_{1,2}\ldots S_{1,W}
S_{2,1}S_{2,2}\ldots S_{2,W}
\vdots
S_{H,1}S_{H,2}\ldots S_{H,W}
Output
Output the answer.
Sample Input 1
9 9 ......... ......... ......... ......... ....#.... ......... ......... ......... .........
Sample Output 1
57
The grid changes as follows through the operations. (The number above represents the operation count. The first ten operations are displayed.)
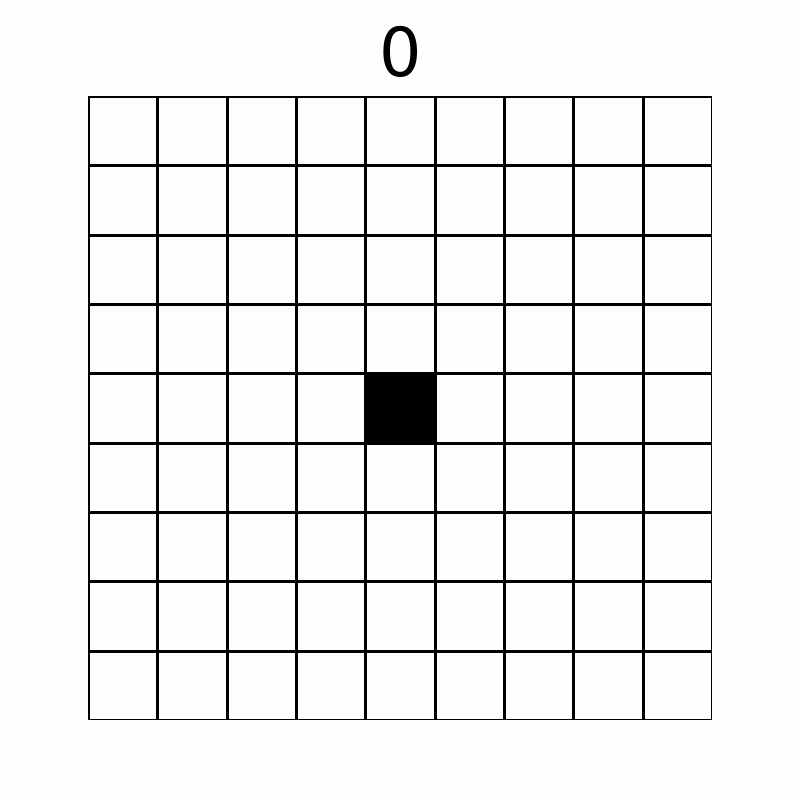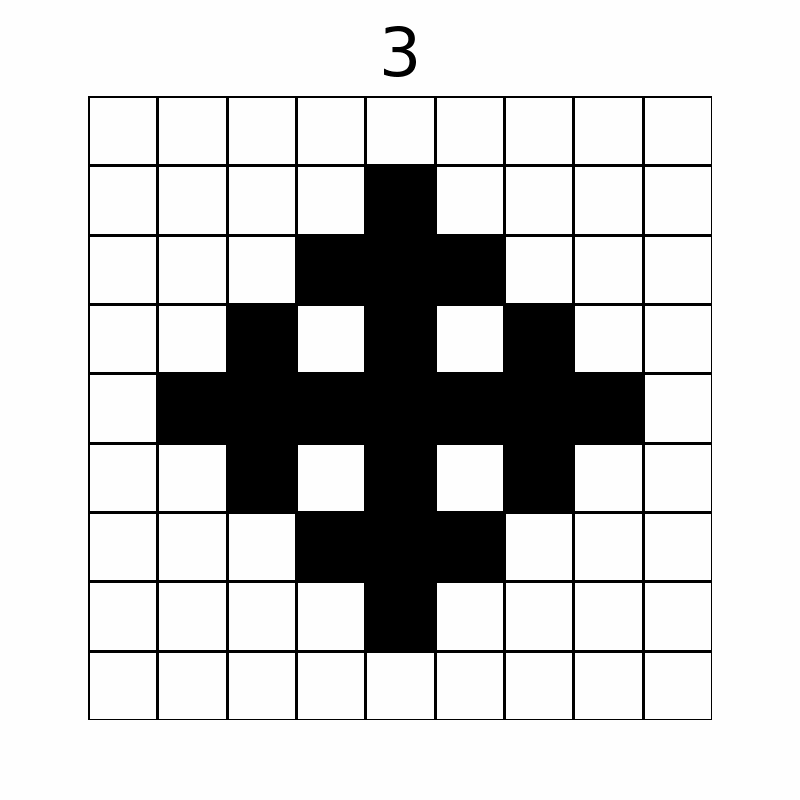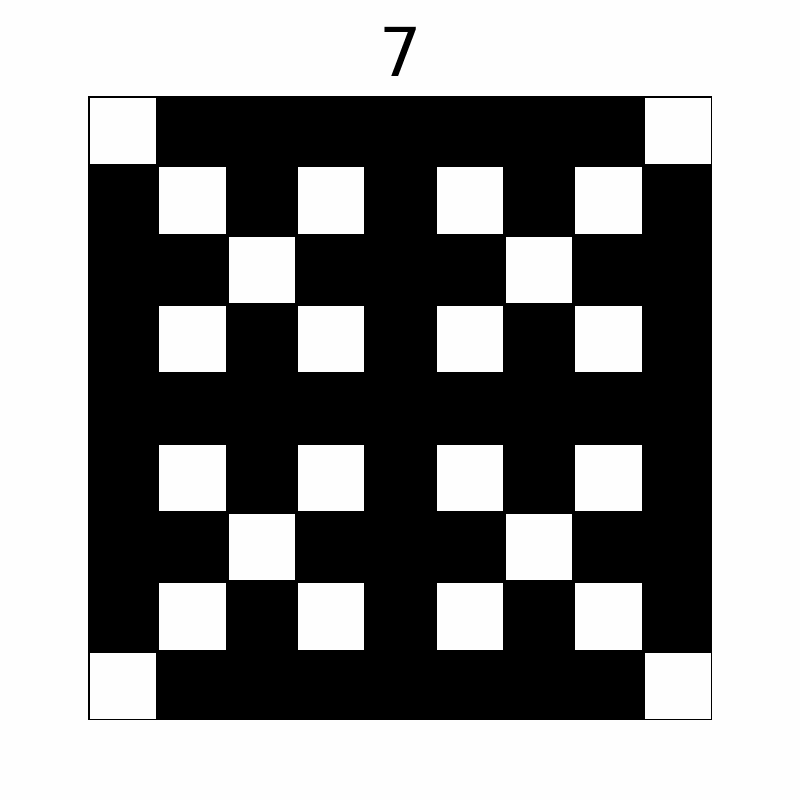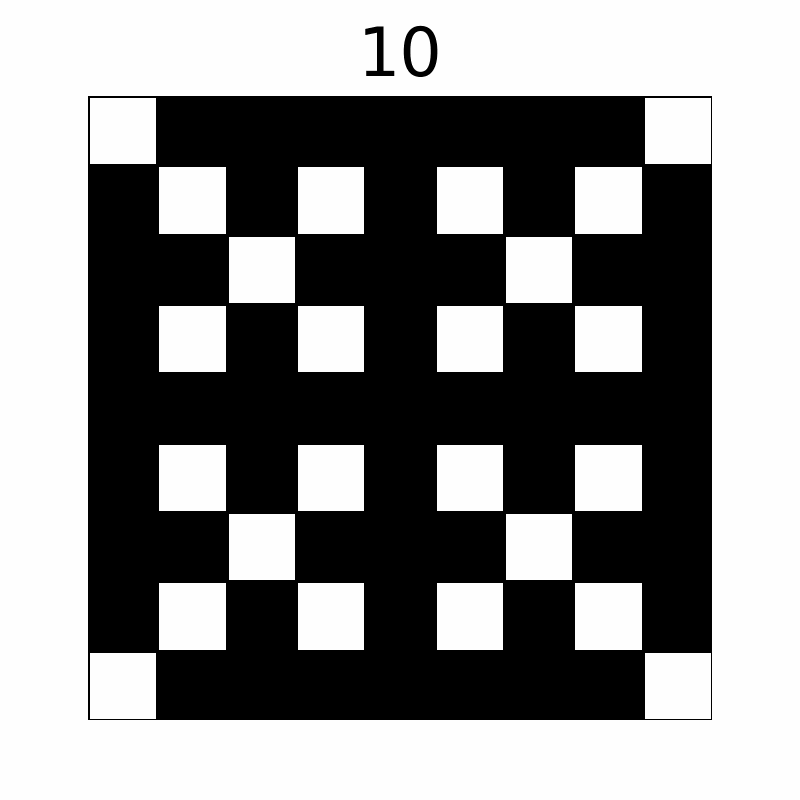
Eventually, 57 cells are colored black.
Sample Input 2
2 2 .. ..
Sample Output 2
0
Sample Input 3
10 10 .......... ....#..... #.......#. ......#... .......#.. .....#.... .......... .......... ..#...#... .......#..
Sample Output 3
64
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 450 点
問題文
正整数 N および長さ N の正整数列 C=(C_1,C_2,\ldots,C_N) が与えられます。
次の条件をすべて満たす正整数列の個数を与えられた正整数 M で割った余りを求めてください。
- 数列の要素はすべて 1 以上 N 以下である。
- 各 i=1,2,\ldots,N に対し、i は数列にちょうど C_i 個含まれる。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。ただし、M は T 個すべてのテストケースにおいて共通です。
制約
- 1\leq T\leq 10^5
- 2\leq M\leq 10^9
- 1\leq N
- 1\leq C_i
- \sum_{i=1}^N C_i\leq 5000
- 全てのテストケースに対する N の総和は 3\times 10^5 以下
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T M
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
i 番目のテストケース \mathrm{case}_i は以下の形式で与えられる。
N C_1 C_2 \ldots C_N
出力
T 行出力せよ。i 行目には i 番目のテストケースの答えを出力せよ。
入力例 1
3 1000000000 2 2 2 5 1 1 1 1 1 6 1 2 3 4 5 6
出力例 1
6 120 230379200
1 番目のテストケースについて、条件を満たす数列は (1,1,2,2),(1,2,1,2),(1,2,2,1),(2,1,1,2),(2,1,2,1),(2,2,1,1) の 6 個です。
入力例 2
3 998244353 1 1 3 4 2 5 10 500 500 500 500 500 500 500 500 500 500
出力例 2
1 6930 261233246
Score : 450 points
Problem Statement
You are given a positive integer N and a sequence of positive integers C=(C_1,C_2,\ldots,C_N) of length N.
Find, modulo a given positive integer M, the number of sequences of positive integers that satisfy all of the following conditions.
- All elements of the sequence are between 1 and N, inclusive.
- For each i=1,2,\ldots,N, the value i appears exactly C_i times in the sequence.
T test cases are given, so find the answer for each. M is common to all T test cases.
Constraints
- 1\leq T\leq 10^5
- 2\leq M\leq 10^9
- 1\leq N
- 1\leq C_i
- \sum_{i=1}^N C_i\leq 5000
- The sum of N over all test cases is at most 3\times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T M
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
The i-th test case, \mathrm{case}_i, is given in the following format:
N C_1 C_2 \ldots C_N
Output
Output T lines. The i-th line should contain the answer for the i-th test case.
Sample Input 1
3 1000000000 2 2 2 5 1 1 1 1 1 6 1 2 3 4 5 6
Sample Output 1
6 120 230379200
For the first test case, the sequences that satisfy the conditions are (1,1,2,2),(1,2,1,2),(1,2,2,1),(2,1,1,2),(2,1,2,1),(2,2,1,1), which is six sequences.
Sample Input 2
3 998244353 1 1 3 4 2 5 10 500 500 500 500 500 500 500 500 500 500
Sample Output 2
1 6930 261233246
Time Limit: 2.5 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
長さ N の英小文字列 T が与えられます。
以下の条件をすべて満たす文字列の列 s=(s_0,s_1,\ldots,s_N) の個数を 998244353 で割った余りを出力してください。
- s_0 は空文字列
- i=1,2,\ldots,N に対し、s_{i} は s_{i-1} の好きな位置(先頭や末尾でもよい)に好きな文字を 1 文字挿入することで得られる文字列
- s_N=T
制約
- 1\leq N\leq 22
- N は整数
- T は長さ N の英小文字列
入力
入力は以下の形式で標準入力から与えられる。
N T
出力
答えを出力せよ。
入力例 1
3 aab
出力例 1
3
条件を満たす s は以下の 3 つです。
- s=(\texttt{""}, \texttt{"a"} ,\texttt{"aa"} ,\texttt{"aab"} )
- s=(\texttt{""}, \texttt{"a"} ,\texttt{"ab"} ,\texttt{"aab"} )
- s=(\texttt{""}, \texttt{"b"} ,\texttt{"ab"} ,\texttt{"aab"} )
入力例 2
7 atcoder
出力例 2
5040
入力例 3
22 atcoderbeginnercontest
出力例 3
115732070
Score : 500 points
Problem Statement
You are given a string T of length N consisting of lowercase English letters.
Output, modulo 998244353, the number of sequences of strings s=(s_0,s_1,\ldots,s_N) that satisfy all of the following conditions.
- s_0 is an empty string.
- For i=1,2,\ldots,N, the string s_{i} is obtained by inserting one arbitrary character at an arbitrary position (possibly beginning or end) in s_{i-1}.
- s_N=T
Constraints
- 1\leq N\leq 22
- N is an integer.
- T is a string of length N consisting of lowercase English letters.
Input
The input is given from Standard Input in the following format:
N T
Output
Output the answer.
Sample Input 1
3 aab
Sample Output 1
3
The sequences s that satisfy the conditions are the following three:
- s=(\texttt{""}, \texttt{"a"} ,\texttt{"aa"} ,\texttt{"aab"} )
- s=(\texttt{""}, \texttt{"a"} ,\texttt{"ab"} ,\texttt{"aab"} )
- s=(\texttt{""}, \texttt{"b"} ,\texttt{"ab"} ,\texttt{"aab"} )
Sample Input 2
7 atcoder
Sample Output 2
5040
Sample Input 3
22 atcoderbeginnercontest
Sample Output 3
115732070
Time Limit: 2.5 sec / Memory Limit: 1024 MiB
配点 : 575 点
問題文
正整数 N,M と長さ N の非負整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
\displaystyle \sum_{x=0}^{M-1} \min_{1\le i\le N} \left(x\oplus A_i \right) を求めてください。
ただし、 x\oplus A_i は x と A_i のビット単位 \mathrm{XOR} を表します。
ビット単位 \mathrm{XOR} 演算とは
非負整数 X,Y のビット単位 \mathrm{XOR} 、X \oplus Y は、以下のように定義されます。
- X \oplus Y を二進表記した際の 2^k (k \geq 0) の位の数は、X,Y を二進表記した際の 2^k の位の数のうち一方のみが 1 であれば 1、そうでなければ 0 である。
制約
- 1\le N\le 2\times 10^5
- 1\le M\le 10^9
- 0\le A_i \le 10^9
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 \ldots A_N
出力
答えを出力せよ。
入力例 1
2 4 1 2
出力例 1
2
- x=0 のとき: x\oplus A_1=1,x\oplus A_2= 2 なので \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 1 です。
- x=1 のとき: x\oplus A_1=0,x\oplus A_2= 3 なので \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 0 です。
- x=2 のとき: x\oplus A_1=3,x\oplus A_2= 0 なので \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 0 です。
- x=3 のとき: x\oplus A_1=2,x\oplus A_2= 1 なので \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 1 です。
したがって、 1+0+0+1=2 を出力してください。
入力例 2
6 5 0 1 2 3 4 5
出力例 2
0
入力例 3
10 8762 347 883 264 816 533 306 190 880 624 279
出力例 3
34912221
Score : 575 points
Problem Statement
You are given positive integers N,M and a sequence of non-negative integers A=(A_1,A_2,\ldots,A_N) of length N.
Find \displaystyle \sum_{x=0}^{M-1} \min_{1\le i\le N} \left(x\oplus A_i \right).
Here, x\oplus A_i represents the bitwise \mathrm{XOR} of x and A_i.
What is bitwise \mathrm{XOR} operation?
The bitwise \mathrm{XOR} of non-negative integers X,Y, X \oplus Y, is defined as follows:
- When X \oplus Y is written in binary, the digit in the 2^k (k \geq 0) place is 1 if exactly one of X,Y has 1 in the 2^k place when written in binary, and 0 otherwise.
Constraints
- 1\le N\le 2\times 10^5
- 1\le M\le 10^9
- 0\le A_i \le 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 A_2 \ldots A_N
Output
Output the answer.
Sample Input 1
2 4 1 2
Sample Output 1
2
- When x=0: x\oplus A_1=1,x\oplus A_2= 2, so \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 1.
- When x=1: x\oplus A_1=0,x\oplus A_2= 3, so \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 0.
- When x=2: x\oplus A_1=3,x\oplus A_2= 0, so \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 0.
- When x=3: x\oplus A_1=2,x\oplus A_2= 1, so \displaystyle \min_{1\le i\le N} \left(x\oplus A_i \right) = 1.
Therefore, output 1+0+0+1=2.
Sample Input 2
6 5 0 1 2 3 4 5
Sample Output 2
0
Sample Input 3
10 8762 347 883 264 816 533 306 190 880 624 279
Sample Output 3
34912221