実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
高橋くんはゲームで遊んでいます。 このゲームにはワールドが 8 つあり、それぞれのワールドにはステージが 8 つずつあります。 ステージには順番があり、最初のステージは 1 個めのワールドにある 1 個めのステージです。 i 個め (1\le i\le 8) のワールドにある j 個め (1\le j\le 8) のステージの次のステージは、以下のようになっています。
- j\lt8 のとき、次のステージは i 個めのワールドにある j+1 個めのステージです。
- i\lt8,j=8 のとき、次のステージは i+1 個めのワールドにある 1 個めのステージです。
- i=8,j=8 のとき、次のステージはありません。このステージが最後のステージです。
i 個め (1\le i\le 8) のワールドにある j 個め (1\le j\le 8) のステージの名前は i-j です。
たとえば、最初のステージ名は 1-1 で、最後のステージ名は 8-8 です。
高橋くんが現在遊んでいるステージのステージ名 S が与えられるので、次のステージのステージ名を出力してください。
制約
- S はいずれかのステージのステージ名である。
- S は
8-8ではない。
入力
入力は以下の形式で標準入力から与えられる。
S
出力
次のステージのステージ名を出力せよ。
入力例 1
4-2
出力例 1
4-3
4 個めのワールドの 2 個めのステージの次のステージは、同じワールドの 3 個めのステージです。
入力例 2
1-8
出力例 2
2-1
1-8 は 1 個めのワールドの最後のステージなので、次のステージは 2 個めのワールドの 1 個めのステージです。
入力例 3
3-3
出力例 3
3-4
Score : 100 points
Problem Statement
Takahashi is playing a game. This game has eight worlds, and each world has eight stages. The stages have an order, and the first stage is the 1st stage in the 1st world. The next stage after the j-th stage (1\le j\le 8) in the i-th world (1\le i\le 8) is as follows:
- When j\lt8, the next stage is the (j+1)-th stage in the i-th world.
- When i\lt8,j=8, the next stage is the 1st stage in the (i+1)-th world.
- When i=8,j=8, there is no next stage. This stage is the last stage.
The name of the j-th stage (1\le j\le 8) in the i-th world (1\le i\le 8) is i-j.
For example, the name of the first stage is 1-1, and the name of the last stage is 8-8.
Given the stage name S of the stage Takahashi is currently playing, output the stage name of the next stage.
Constraints
- S is the stage name of one of the stages.
- S is not
8-8.
Input
The input is given from Standard Input in the following format:
S
Output
Output the stage name of the next stage.
Sample Input 1
4-2
Sample Output 1
4-3
The next stage after the 2nd stage in the 4th world is the 3rd stage in the same world.
Sample Input 2
1-8
Sample Output 2
2-1
1-8 is the last stage in the 1st world, so the next stage is the 1st stage in the 2nd world.
Sample Input 3
3-3
Sample Output 3
3-4
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
縦 H マス、横 W マスのマス目があります。 上から i 行目 (1\le i\le H) 、左から j 列目 (1\le j\le W) のマスをマス (i,j) と呼ぶことにします。
それぞれのマスは白もしくは黒のどちらか 1 色で塗られています。
マスに塗られている色は H 個の文字列 S _ 1,S _ 2,\ldots,S _ H で表され、S _ i\ (1\le i\le H) の j 文字目 (1\le j\le W) が . のとき、マス (i,j) は白で塗られており、S _ i\ (1\le i\le H) の j 文字目 (1\le j\le W) が # のとき、マス (i,j) は黒で塗られています。
マス目が以下の条件を満たすか判定してください。
- どの黒で塗られたマスについても、上下左右で隣り合うマスのうち黒く塗られているものは 2 つもしくは 4 つである。
ただし、マス (i,j)\ (1\le i\le H,1\le j\le W) とマス (k,l)\ (1\le k\le H,1\le l\le W) は、|i-k|+|j-l|=1 であるとき、かつそのときに限り上下左右で隣り合っているとします。
制約
- 1\le H\le 20
- 1\le W\le 20
- H,W は整数
- S _ i は
.および#からなる長さ W の文字列 (1\le i\le H)
入力
入力は以下の形式で標準入力から与えられる。
H W S _ 1 S _ 2 \vdots S _ H
出力
与えられたマス目が条件を満たしているとき Yes を、条件を満たしていないとき No を出力せよ。
入力例 1
8 7 .###### ##....# #.###.# #.#.#.# #.#.#.# #.##### #...#.. #####..
出力例 1
Yes
例えば、マス (6,3) は黒で塗られており、隣り合っているマス (5,3),(6,2),(6,4),(7,3) のうち、マス (5,3) およびマス (6,4) の 2 マスが黒で塗られているため、条件を満たしています。
他の黒で塗られたどのマスについても条件を満たしているため、Yes を出力してください。
入力例 2
1 2 ##
出力例 2
No
マス (1,1) は黒で塗られていますが、隣り合っているマスは 1 つしかないため、条件を満たしていません。
よって、No を出力して下さい。
入力例 3
4 3 ... ... ... ...
出力例 3
Yes
黒で塗られているマスがないため、条件を満たしています。
よって、Yes を出力してください。
入力例 4
15 18 ##.###..##.##..##. ##.#.##.##.##.#### ...##.#.......#### ###.###....###.##. #.##.......#.#.... #..#.##.##.#.#.... #.########.####.## #.##.##.#....##.## #......##......... ##.##..#..##..#### .#.#####..#####..# .#..#...##.#.....# .#..#.####.#.....# .##.#.#.#..##..### ..###.###...####..
出力例 4
Yes
Score : 200 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row (1\le i\le H) from the top and the j-th column (1\le j\le W) from the left.
Each cell is painted with one color, white or black.
The color painted on the cells is represented by H strings S _ 1,S _ 2,\ldots,S _ H. When the j-th character (1\le j\le W) of S _ i\ (1\le i\le H) is ., cell (i,j) is painted white, and when the j-th character (1\le j\le W) of S _ i\ (1\le i\le H) is #, cell (i,j) is painted black.
Determine whether the grid satisfies the following condition:
- For every black cell, the number of horizontally or vertically adjacent cells that are painted black is 2 or 4.
Here, cells (i,j)\ (1\le i\le H,1\le j\le W) and (k,l)\ (1\le k\le H,1\le l\le W) are horizontally or vertically adjacent if and only if |i-k|+|j-l|=1.
Constraints
- 1\le H\le 20
- 1\le W\le 20
- H and W are integers.
- S _ i is a string of length W consisting of
.and#(1\le i\le H).
Input
The input is given from Standard Input in the following format:
H W S _ 1 S _ 2 \vdots S _ H
Output
Output Yes if the given grid satisfies the condition, and No if it does not satisfy the condition.
Sample Input 1
8 7 .###### ##....# #.###.# #.#.#.# #.#.#.# #.##### #...#.. #####..
Sample Output 1
Yes
For example, cell (6,3) is painted black, and among the adjacent cells (5,3),(6,2),(6,4),(7,3), cells (5,3) and (6,4) are painted black, which is 2 cells, so it satisfies the condition.
Every other black cell also satisfies the condition, so output Yes.
Sample Input 2
1 2 ##
Sample Output 2
No
Cell (1,1) is painted black, but it has only one adjacent cell, so it does not satisfy the condition.
Therefore, output No.
Sample Input 3
4 3 ... ... ... ...
Sample Output 3
Yes
There are no black cells, so the condition is satisfied.
Therefore, output Yes.
Sample Input 4
15 18 ##.###..##.##..##. ##.#.##.##.##.#### ...##.#.......#### ###.###....###.##. #.##.......#.#.... #..#.##.##.#.#.... #.########.####.## #.##.##.#....##.## #......##......... ##.##..#..##..#### .#.#####..#####..# .#..#...##.#.....# .#..#.####.#.....# .##.#.#.#..##..### ..###.###...####..
Sample Output 4
Yes
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
高橋くんは、文字をいくつか持っています。
高橋くんが持っている文字は A, B, C のいずれかです。
はじめ、高橋くんは A を n _ A 個、B を n _ B 個、C を n _ C 個持っています。
高橋くんは、A を 1 つ、C を 1 つ、さらに追加で任意の 1 つの文字の合計 3 文字を使うことで、コンテストを 1 つ開催することができます。
具体的には、A を 2 つ、C を 1 つ使うと AAC を、A, B, C を 1 つずつ使うと ABC を、A を 1 つ、C を 2 つ使うと ACC を開催することができます。
高橋くんは、現在持っている文字を使ってコンテストをなるべく多く開催したいです。 高橋くんが最大でいくつのコンテストを開催することができるか求めてください。
T 個のテストケースが与えられるので、それぞれについて答えてください。
制約
- 1\le T\le2\times10 ^ 5
- それぞれのテストケースについて、
- 0\le n _ A\le10 ^ 9
- 0\le n _ B\le10 ^ 9
- 0\le n _ C\le10 ^ 9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{testcase} _ 1
\mathrm{testcase} _ 2
\vdots
\mathrm{testcase} _ T
\mathrm{testcase} _ i\ (1\le i\le T) は i 番目のテストケースを表しており、次の形式で与えられる。
n _ A n _ B n _ C
出力
T 行にわたって出力せよ。 i 行目 (1\le i\le T) には、i 番目のテストケースの答えを出力せよ。
入力例 1
5 3 1 2 100 0 0 1000000 1000000 1000000 31 41 59 1000000000 10000 1
出力例 1
2 0 1000000 31 1
1 つめのテストケースでは、AAC を 1 回、ABC を 1 回の計 2 回のコンテストを開催することができます。
よって、1 行目には 2 を出力してください。
Score : 300 points
Problem Statement
Takahashi has some letters.
Each letter he has is A, B, or C.
Initially, he has n _ A letters A, n _ B letters B, and n _ C letters C.
He can hold one contest by using one letter A, one letter C, and additionally any one letter, for a total of three letters.
Specifically, he can hold AAC by using two letters A and one letter C, ABC by using one letter each of A, B, and C, and ACC by using one letter A and two letters C.
He wants to hold as many contests as possible using the letters he currently has. Find the maximum number of contests he can hold.
T test cases are given, so report the answer for each of them.
Constraints
- 1\le T\le2\times10 ^ 5
- For each test case,
- 0\le n _ A\le10 ^ 9
- 0\le n _ B\le10 ^ 9
- 0\le n _ C\le10 ^ 9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\mathrm{testcase} _ 1
\mathrm{testcase} _ 2
\vdots
\mathrm{testcase} _ T
\mathrm{testcase} _ i\ (1\le i\le T) represents the i-th test case and is given in the following format:
n _ A n _ B n _ C
Output
Output over T lines. On the i-th line (1\le i\le T), output the answer to the i-th test case.
Sample Input 1
5 3 1 2 100 0 0 1000000 1000000 1000000 31 41 59 1000000000 10000 1
Sample Output 1
2 0 1000000 31 1
In the first test case, he can hold AAC once and ABC once, for a total of two contests.
Therefore, output 2 on the first line.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
N を正整数とします。長さ 2^N の非負整数列 A=(A_1, A_2, \dots, A_{2^N}) の アンバランスさ を次の操作によって得られる非負整数値として定義します。
- はじめ、X=0 とする。
- 次の一連の操作を N 回行う。
- X を \max(X, \max(A) - \min(A)) に更新する。ここで \max(A) および \min(A) は数列 A の最大値と最小値を意味する。
- 先頭から順に 2 つずつ要素を組にして、それらの和を並べることでできる長さが A の半分の数列を、新たな A とする。すなわち、A \gets (A_1 + A_2, A_3 + A_4, \dots, A_{\vert A \vert - 1} + A_{\vert A \vert}) とする。
- 最終的な X をアンバランスさとする。
例えば N=2, A=(6, 8, 3, 5) は以下の手順によりアンバランスさが 6 であるとわかります。
- はじめ、X=0 である。
- 1 回目の一連の操作は次の通りである。
- X を \max(X, \max(A) - \min(A)) = \max(0, 8 - 3) = 5 に更新する。
- A を (6+8, 3+5) = (14, 8) とする。
- 2 回目の一連の操作は次の通りである。
- X を \max(X, \max(A) - \min(A)) = \max(5, 14 - 8) = 6 に更新する。
- A を (14 + 8) = (22) とする。
- 最終的に X=6 となる。
非負整数 K が与えられます。長さ 2^N の非負整数列であって総和が K であるものの中で、アンバランスさが最小値を取る数列を構成してください。
制約
- 1 \leq N \leq 20
- 0 \leq K \leq 10^9
- N, K は整数
入力
入力は以下の形式で標準入力から与えられる。
N K
出力
アンバランスさが最小値を取る数列を B=(B_1,B_2,\dots,B_{2^N}) とする。B のアンバランスさを U とする。この時、以下の形式で答えを出力せよ。
U
B_1 B_2 \dots B_{2^N}
答えが複数ある場合は、どれを出力しても正答とみなされる。
入力例 1
1 11
出力例 1
1 5 6
(5, 6) はアンバランスさが 1 の数列で、これが条件を満たす数列のうちアンバランスさが最小の数列です。
入力例 2
3 56
出力例 2
0 7 7 7 7 7 7 7 7
Score : 400 points
Problem Statement
Let N be a positive integer. Define the imbalance of a sequence A=(A_1, A_2, \dots, A_{2^N}) of non-negative integers of length 2^N as the non-negative integer value obtained by the following operation:
- Initially, set X=0.
- Perform the following series of operations N times:
- Update X to \max(X, \max(A) - \min(A)), where \max(A) and \min(A) denote the maximum and minimum values of sequence A, respectively.
- Form a new sequence of half the length by pairing elements from the beginning two by two and arranging their sums. That is, set A \gets (A_1 + A_2, A_3 + A_4, \dots, A_{\vert A \vert - 1} + A_{\vert A \vert}).
- The final value of X is the imbalance.
For example, when N=2, A=(6, 8, 3, 5), the imbalance is 6 through the following steps:
- Initially, X=0.
- The first series of operations is as follows:
- Update X to \max(X, \max(A) - \min(A)) = \max(0, 8 - 3) = 5.
- Set A to (6+8, 3+5) = (14, 8).
- The second series of operations is as follows:
- Update X to \max(X, \max(A) - \min(A)) = \max(5, 14 - 8) = 6.
- Set A to (14 + 8) = (22).
- Finally, X=6.
You are given a non-negative integer K. Among all sequences of non-negative integers of length 2^N with sum K, construct a sequence that minimizes the imbalance.
Constraints
- 1 \leq N \leq 20
- 0 \leq K \leq 10^9
- N and K are integers.
Input
The input is given from Standard Input in the following format:
N K
Output
Let B=(B_1,B_2,\dots,B_{2^N}) be a sequence with minimum imbalance. Let U be the imbalance of B. Output a solution in the following format:
U
B_1 B_2 \dots B_{2^N}
If there are multiple solutions, any of them will be considered correct.
Sample Input 1
1 11
Sample Output 1
1 5 6
(5, 6) is a sequence with imbalance 1, which is the minimum imbalance among sequences satisfying the condition.
Sample Input 2
3 56
Sample Output 2
0 7 7 7 7 7 7 7 7
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 450 点
問題文
2 次元平面上に N 個の点があります。N は奇数です。 i 番目の点は (x_i, y_i) にあります。全ての点の座標は相異なります。
N 個の点のうち過半数を通る直線が存在するかを判定して、存在すればそれを出力してください。
なお、制約を満たすどのような入力においても、条件を満たす直線が存在する場合、その直線は -10^{18} 以上 10^{18} 以下の整数 a,b,c を用いて ax+by+c=0 と表すことができます。(ただし (a,b,c) \neq (0,0,0)) この a,b,c を出力してください。
制約
- 3 \leq N \leq 5 \times 10^5
- N は奇数
- -10^8 \leq x_i \leq 10^8
- -10^8 \leq y_i \leq 10^8
- i \neq j ならば (x_i, y_i) \neq (x_j, y_j)
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N x_1 y_1 x_2 y_2 \vdots x_N y_N
出力
条件を満たす直線が存在しない場合は No を出力せよ。
条件を満たす直線が存在する場合は 2 行出力せよ。1 行目には Yes を出力して、2 行目には a,b,c をこの順に空白区切りで出力せよ。a,b,c は -10^{18} 以上 10^{18} 以下かつ (a,b,c) \neq (0,0,0) である必要がある点に注意せよ。
答えが複数ある場合はどれを出力しても正答とみなされる。
入力例 1
3 1 1 3 2 2 4
出力例 1
Yes 2 1 -8
直線 2x+y-8=0 は 2 番目の点と 3 番目の点を通るので条件を満たします。
入力例 2
5 5 2 1 3 2 6 4 4 5 4
出力例 2
No
条件を満たす直線は存在しません。
入力例 3
11 -9374372 85232388 -60705467 86198234 -7475320 80628487 98066347 -23868213 -12177678 85284287 30535572 -35358356 51324557 22410787 28854279 44658587 -28804873 82911971 65052073 8819187 -67744430 68365758
出力例 3
Yes 4655800 4702358 -344340416016346
Score : 450 points
Problem Statement
There are N points on a two-dimensional plane. N is odd. The i-th point is at (x_i, y_i). All point coordinates are distinct.
Determine whether there exists a line passing through more than half of the N points, and if so, output it.
For any input satisfying the constraints, if a line satisfying the condition exists, it can be expressed as ax+by+c=0 using integers a,b,c with -10^{18} \leq a,b,c \leq 10^{18} (where (a,b,c) \neq (0,0,0)). Output these a,b,c.
Constraints
- 3 \leq N \leq 5 \times 10^5
- N is odd.
- -10^8 \leq x_i \leq 10^8
- -10^8 \leq y_i \leq 10^8
- If i \neq j, then (x_i, y_i) \neq (x_j, y_j).
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N x_1 y_1 x_2 y_2 \vdots x_N y_N
Output
If no line satisfying the condition exists, output No.
If a line satisfying the condition exists, output two lines. On the first line, output Yes, and on the second line, output a,b,c in this order separated by spaces. a,b,c must satisfy -10^{18} \leq a,b,c \leq 10^{18} and (a,b,c) \neq (0,0,0).
If there are multiple solutions, any of them will be considered correct.
Sample Input 1
3 1 1 3 2 2 4
Sample Output 1
Yes 2 1 -8
The line 2x+y-8=0 passes through the 2nd and 3rd points, so it satisfies the condition.
Sample Input 2
5 5 2 1 3 2 6 4 4 5 4
Sample Output 2
No
No line satisfying the condition exists.
Sample Input 3
11 -9374372 85232388 -60705467 86198234 -7475320 80628487 98066347 -23868213 -12177678 85284287 30535572 -35358356 51324557 22410787 28854279 44658587 -28804873 82911971 65052073 8819187 -67744430 68365758
Sample Output 3
Yes 4655800 4702358 -344340416016346
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
N 頂点 M 辺の連結無向グラフがあります。 頂点には頂点 1, 頂点 2,\ldots, 頂点 N と番号付けられており、i 番目 (1\le i\le M) の辺は頂点 u _ i と頂点 v _ i を結んでいます。
i=1,2,\ldots,N について次の問題を解いてください。
はじめ、高橋くんの体重は 0 です。
高橋くんは、車に乗って頂点 1 に訪れ、頂点 i に向かって移動を行います。 高橋くんが頂点 v\ (1\le v\le N) に訪れるとき、高橋くんの体重は W _ v だけ増加します。
高橋くんが乗っている車は辺に沿って移動することができます。 高橋くんが辺を通過するとき、そのときの高橋くんの体重を X として、車は燃料を X 消費します。
高橋くんが頂点 i にたどり着くために消費する燃料の量の最小値を求めてください。
制約
- 1\le N\le5000
- 1\le M\le5000
- 1\le W _ i\le10 ^ 9\ (1\le i\le N)
- 1\le u _ i\le v _ i\le N\ (1\le i\le M)
- 与えられるグラフは連結
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M W _ 1 W _ 2 \ldots W _ N u _ 1 v _ 1 u _ 2 v _ 2 \vdots u _ M v _ M
出力
N 行にわたって出力せよ。 i 行目 (1\le i\le N) には、高橋くんが頂点 i にたどり着くのに必要な燃料の量を出力せよ。
入力例 1
5 6 3 1 4 1 5 1 2 1 3 2 3 2 4 3 5 4 5
出力例 1
0 3 3 7 10
与えられたグラフは以下のようになります。
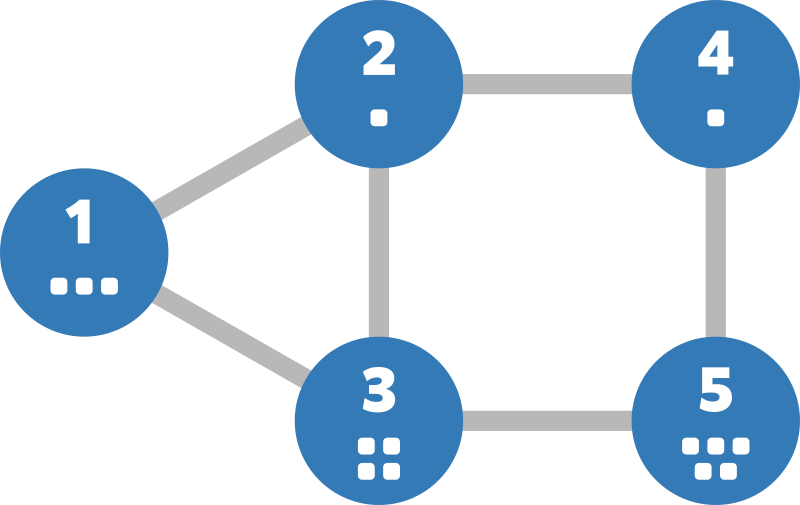
例えば、高橋くんは頂点 1 に訪れてから次のように行動することで頂点 5 にたどり着くことができます。
- 高橋くんが頂点 1 に訪れる。高橋くんの体重が 3 増加し、3 になる。
- 高橋くんが燃料を 3 消費して頂点 3 に移動する。高橋くんの体重が 4 増加し、7 になる。
- 高橋くんが燃料を 7 消費して頂点 5 に移動する。高橋くんの体重が 5 増加し、12 になる。
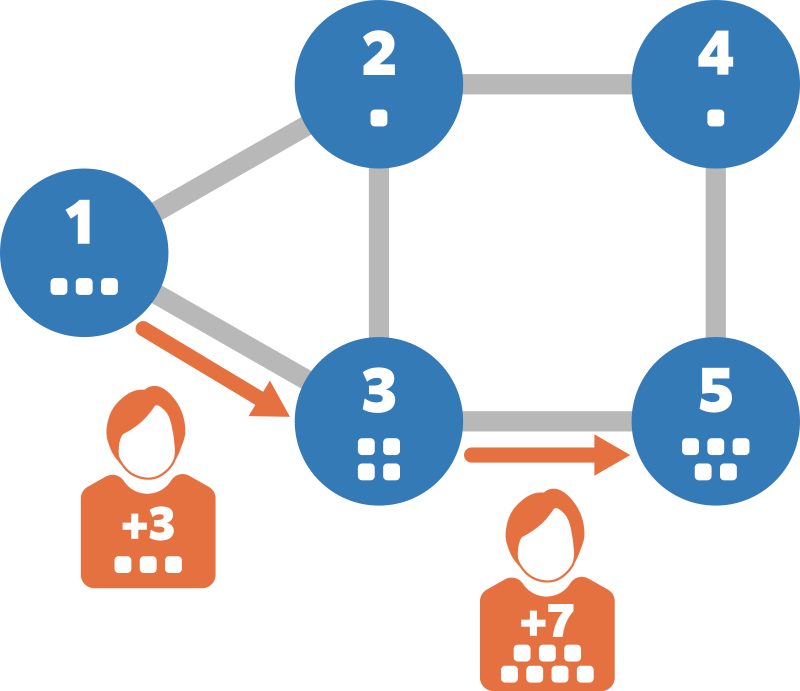
このように行動することで燃料を 10 だけ消費して頂点 5 にたどり着くことができます。 消費する燃料を 9 以下にすることはできないため、5 行目には 10 を出力してください。
入力例 2
5 4 1000000000 1000000000 1000000000 1000000000 1000000000 1 2 2 3 3 4 4 5
出力例 2
0 1000000000 3000000000 6000000000 10000000000
答えが 2 ^ {32} を越える場合があることに注意してください。
入力例 3
10 20 74931 58277 33783 91022 53003 11085 65924 63548 78622 77307 1 8 3 6 5 10 4 6 1 3 1 7 2 6 7 10 8 9 3 4 4 4 4 6 6 6 5 10 1 7 4 5 1 2 3 7 2 3 5 8
出力例 3
0 74931 74931 183645 213410 183645 74931 74931 213410 215786
Score : 500 points
Problem Statement
There is a connected undirected graph with N vertices and M edges. The vertices are numbered vertex 1, vertex 2,\ldots, vertex N, and the i-th edge (1\le i\le M) connects vertices u _ i and v _ i.
For i=1,2,\ldots,N, solve the following problem:
Initially, Takahashi's weight is 0.
He travels by car to visit vertex 1 and moves toward vertex i. When he visits vertex v\ (1\le v\le N), his weight increases by W _ v.
The car he is riding can move along the edges. When he passes through an edge, letting X be his weight at that time, the car consumes X fuel.
Find the minimum amount of fuel consumed for him to reach vertex i.
Constraints
- 1\le N\le5000
- 1\le M\le5000
- 1\le W _ i\le10 ^ 9\ (1\le i\le N)
- 1\le u _ i\le v _ i\le N\ (1\le i\le M)
- The given graph is connected.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M W _ 1 W _ 2 \ldots W _ N u _ 1 v _ 1 u _ 2 v _ 2 \vdots u _ M v _ M
Output
Output over N lines. On the i-th line (1\le i\le N), output the amount of fuel needed for Takahashi to reach vertex i.
Sample Input 1
5 6 3 1 4 1 5 1 2 1 3 2 3 2 4 3 5 4 5
Sample Output 1
0 3 3 7 10
The given graph is as follows:

For example, Takahashi can reach vertex 5 by visiting vertex 1 and then acting as follows:
- He visits vertex 1. His weight increases by 3, becoming 3.
- He consumes 3 fuel to move to vertex 3. His weight increases by 4, becoming 7.
- He consumes 7 fuel to move to vertex 5. His weight increases by 5, becoming 12.

By acting this way, he can reach vertex 5 by consuming 10 fuel. It is impossible to reduce the fuel consumption to 9 or less, so output 10 on the 5th line.
Sample Input 2
5 4 1000000000 1000000000 1000000000 1000000000 1000000000 1 2 2 3 3 4 4 5
Sample Output 2
0 1000000000 3000000000 6000000000 10000000000
Note that the answer may exceed 2 ^ {32}.
Sample Input 3
10 20 74931 58277 33783 91022 53003 11085 65924 63548 78622 77307 1 8 3 6 5 10 4 6 1 3 1 7 2 6 7 10 8 9 3 4 4 4 4 6 6 6 5 10 1 7 4 5 1 2 3 7 2 3 5 8
Sample Output 3
0 74931 74931 183645 213410 183645 74931 74931 213410 215786
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 575 点
問題文
正整数 A, B, C, N が与えられます。
問題 1 および問題 2 をそれぞれ解いてください。(問題 1 と問題 2 で異なる箇所は太字で表記しています)
問題 1
N 個のボールがあります。ボール同士は区別できません。 また、箱 1、箱 2、箱 3 があります。
次の条件を満たすように箱に全てのボールを入れる方法の個数を 998244353 で割った余りを求めてください。
- 箱 1 に入っているボールの個数は A の倍数である。
- 箱 2 に入っているボールの個数は B の倍数である。
- 箱 3 に入っているボールの個数は C の倍数である。
ただし、2 つのボールを入れる方法は、入っているボールの個数が 2 つの方法の間で異なる箱が存在する時に 別々に数えます。
問題 2
1 から N までの番号のついた N 個のボールがあります。ボール同士は区別できます。 また、箱 1、箱 2、箱 3 があります。
次の条件を満たすように箱に全てのボールを入れる方法の個数を 998244353 で割った余りを求めてください。
- 箱 1 に入っているボールの個数は A の倍数である。
- 箱 2 に入っているボールの個数は B の倍数である。
- 箱 3 に入っているボールの個数は C の倍数である。
ただし、2 つのボールを入れる方法は、入っている箱が 2 つの方法の間で異なるボールが存在する時に 別々に数えます。
制約
- 1 \leq N \leq 3 \times 10^5
- 1 \leq A \leq 3 \times 10^5
- 1 \leq B \leq 3 \times 10^5
- 1 \leq C \leq 3 \times 10^5
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A B C
出力
2 行出力せよ。i 行目には問題 i への答えを出力せよ。
入力例 1
3 1 2 3
出力例 1
3 5
問題 1 において条件を満たすボールの入れ方は次の 3 通りです。
- 箱 1 に 3 個のボールを入れる。
- 箱 1 に 1 個、箱 2 に 2 個のボールを入れる。
- 箱 3 に 3 個のボールを入れる。
問題 2 において条件を満たすボールの入れ方は次の 5 通りです。
- 箱 1 にボール 1,2,3 を入れる。
- 箱 1 にボール 1 を、箱 2 にボール 2,3 を入れる。
- 箱 1 にボール 2 を、箱 2 にボール 1,3 を入れる。
- 箱 1 にボール 3 を、箱 2 にボール 1,2 を入れる。
- 箱 3 にボール 1,2,3 を入れる。
入力例 2
1234 56 7 89
出力例 2
15 535248725
入力例 3
300000 6 490 420
出力例 3
73339 760083042
入力例 4
12345 67 89 123456
出力例 4
2 150951502
Score : 575 points
Problem Statement
You are given positive integers A, B, C, N.
Solve Problems 1 and 2. (The differences between the problems are indicated in bold.)
Problem 1
There are N balls. The balls are indistinguishable from each other. Also, there are boxes 1, 2, and 3.
Find the number, modulo 998244353, of ways to put all balls into the boxes satisfying the following conditions.
- The number of balls in box 1 is a multiple of A.
- The number of balls in box 2 is a multiple of B.
- The number of balls in box 3 is a multiple of C.
Here, two ways of putting balls are counted separately when there exists a box where the number of balls differs between the two ways.
Problem 2
There are N balls numbered from 1 to N. The balls are distinguishable from each other. Also, there are boxes 1, 2, and 3.
Find the number, modulo 998244353, of ways to put all balls into the boxes satisfying the following conditions.
- The number of balls in box 1 is a multiple of A.
- The number of balls in box 2 is a multiple of B.
- The number of balls in box 3 is a multiple of C.
Here, two ways of putting balls are counted separately when there exists a ball whose box differs between the two ways.
Constraints
- 1 \leq N \leq 3 \times 10^5
- 1 \leq A \leq 3 \times 10^5
- 1 \leq B \leq 3 \times 10^5
- 1 \leq C \leq 3 \times 10^5
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A B C
Output
Output two lines. On the i-th line, output the answer to Problem i.
Sample Input 1
3 1 2 3
Sample Output 1
3 5
In Problem 1, the ways of putting balls that satisfy the condition are the following three ways:
- Put 3 balls in box 1.
- Put 1 ball in box 1 and 2 balls in box 2.
- Put 3 balls in box 3.
In Problem 2, the ways of putting balls that satisfy the condition are the following five ways:
- Put balls 1,2,3 in box 1.
- Put ball 1 in box 1 and balls 2,3 in box 2.
- Put ball 2 in box 1 and balls 1,3 in box 2.
- Put ball 3 in box 1 and balls 1,2 in box 2.
- Put balls 1,2,3 in box 3.
Sample Input 2
1234 56 7 89
Sample Output 2
15 535248725
Sample Input 3
300000 6 490 420
Sample Output 3
73339 760083042
Sample Input 4
12345 67 89 123456
Sample Output 4
2 150951502