Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
英小文字からなる N 文字の文字列 S が与えられます。
S の先頭から A 文字、末尾から B 文字取り除いた N-A-B 文字の文字列を出力してください。
制約
- 1\le N\le20
- 0\le A
- 0\le B
- A+B\lt N
- S は英小文字からなる N 文字の文字列
- N,A,B はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A B S
出力
S の先頭から A 文字、末尾から B 文字取り除いた文字列を出力せよ。
入力例 1
7 1 3 atcoder
出力例 1
tco
atcoder の先頭から 1 文字、末尾から 3 文字取り除くと tco になります。
入力例 2
1 0 0 a
出力例 2
a
出力すべき文字列が S と等しい場合もあります。
入力例 3
20 4 8 abcdefghijklmnopqrst
出力例 3
efghijkl
Score : 100 points
Problem Statement
You are given an N-character string S consisting of lowercase English letters.
Output the string of N-A-B characters obtained by removing the first A characters and the last B characters from S.
Constraints
- 1\le N\le20
- 0\le A
- 0\le B
- A+B\lt N
- S is a string of N characters consisting of lowercase English letters.
- N, A, and B are all integers.
Input
The input is given from Standard Input in the following format:
N A B S
Output
Output the string obtained by removing the first A characters and the last B characters from S.
Sample Input 1
7 1 3 atcoder
Sample Output 1
tco
Removing the first one character and the last three characters from atcoder gives tco.
Sample Input 2
1 0 0 a
Sample Output 2
a
The string to be output may be equal to S.
Sample Input 3
20 4 8 abcdefghijklmnopqrst
Sample Output 3
efghijkl
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
高橋君は長さ N の整数列 A=(A_1,A_2,\ldots,A_N) を持っています。
A は広義単調増加であることが保証されます。
高橋君はこの整数列に対して M 回操作を行います。 i 回目 (1\leq i\leq M) の操作では、次の操作を行います。
数列 A が B_i を要素として持つならば、そのような要素を 1 つ選び、削除する。 そのような要素が存在しないならば何もしない。
A は広義単調増加であるため、操作後の列は要素の選び方によらず一意であり、再び広義単調増加となることに注意せよ。
M 回の操作を行なった後の A を求めてください。
広義単調増加 とは
数列 X=(X_1,X_2,\ldots,X_K) が広義単調増加であるとは、 任意の i (1\leq i\leq K-1) について、 X_i\leq X_{i+1} をみたすことを指します。制約
- 1 \leq N \leq 100
- 1 \leq M \leq 100
- 1 \leq A_i,B_i \leq 10^9
- 整数列 A は広義単調増加である。
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 \ldots A_N B_1 B_2 \ldots B_M
出力
操作後の A の各要素を、順に空白区切りで一行に出力せよ。
操作後の A が空ならば、何も出力しないようにせよ。
入力例 1
8 5 1 2 2 3 3 3 5 6 2 2 7 3 2
出力例 1
1 3 3 5 6
最初、A は A=(1,2,2,3,3,3,5,6) です。
操作は次のように行われます。
- A から 2 を 1 つ削除し、操作後の A は A=(1,2,3,3,3,5,6) となります。
- A から 2 を 1 つ削除し、操作後の A は A=(1,3,3,3,5,6) となります。
- A は 7 を要素として持たないため、何も行いません。操作後の A は A=(1,3,3,3,5,6) のままです。
- A から 3 を 1 つ削除し、操作後の A は A=(1,3,3,5,6) となります。
- A は 2 を要素として持たないため、何も行いません。操作後の A は A=(1,3,3,5,6) のままです。
よって、すべての操作の後、A=(1,3,3,5,6) であるため、要素をこの順に空白区切りで出力します。
入力例 2
1 2 1 1 1
出力例 2
操作後の A は空となるため、何も出力しません。
Score : 200 points
Problem Statement
Takahashi has an integer sequence A=(A_1,A_2,\ldots,A_N) of length N.
It is guaranteed that A is non-decreasing.
Takahashi performs M operations on this integer sequence. In the i-th operation (1\leq i\leq M), he performs the following operation:
If the sequence A contains B_i as an element, select one such element and delete it. If no such element exists, do nothing.
Note that since A is non-decreasing, the sequence after the operation is uniquely determined regardless of the choice of element, and remains non-decreasing.
Find A after performing M operations.
What is non-decreasing?
A sequence X=(X_1,X_2,\ldots,X_K) is non-decreasing if X_i\leq X_{i+1} holds for all i (1\leq i\leq K-1).Constraints
- 1 \leq N \leq 100
- 1 \leq M \leq 100
- 1 \leq A_i,B_i \leq 10^9
- The integer sequence A is non-decreasing.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 A_2 \ldots A_N B_1 B_2 \ldots B_M
Output
Output the elements of A after the operations, in order, separated by spaces on a single line.
If A is empty after the operations, output nothing.
Sample Input 1
8 5 1 2 2 3 3 3 5 6 2 2 7 3 2
Sample Output 1
1 3 3 5 6
Initially, A is A=(1,2,2,3,3,3,5,6).
The operations are performed as follows:
- Delete one 2 from A, and A becomes A=(1,2,3,3,3,5,6) after the operation.
- Delete one 2 from A, and A becomes A=(1,3,3,3,5,6) after the operation.
- Since A does not contain 7 as an element, do nothing. A remains A=(1,3,3,3,5,6) after the operation.
- Delete one 3 from A, and A becomes A=(1,3,3,5,6) after the operation.
- Since A does not contain 2 as an element, do nothing. A remains A=(1,3,3,5,6) after the operation.
Therefore, after all operations, A=(1,3,3,5,6), so output the elements in this order separated by spaces.
Sample Input 2
1 2 1 1 1
Sample Output 2
A becomes empty after the operations, so output nothing.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
長さ N の整数列 A=(A _ 1,A _ 2,\ldots,A _ N) が与えられます。
整数の 2 つ組 (i,j)\ (1\le i\lt j\le N) のうち、j-i=A _ i+A _ j を満たすものがいくつあるか求めてください。
制約
- 1\le N\le2\times10 ^ 5
- 1\le A _ i\le2\times10 ^ 5\ (1\le i\le N)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A _ 1 A _ 2 \ldots A _ N
出力
答えを出力せよ。
入力例 1
9 3 1 4 1 5 9 2 6 5
出力例 1
3
例えば、(i,j)=(4,7) とすると、j-i=7-4=3 かつ A _ i+A _ j=1+2=3 が成り立つので、j-i=A _ i+A _ j です。
一方で、(i,j)=(3,8) とすると、j-i=8-3=5 かつ A _ i+A _ j=4+6=10 となるので、j-i\ne A _ i+A _ j です。
(i,j)=(1,9),(2,4),(4,7) の 3 組だけが条件を満たすので、3 を出力してください。
入力例 2
3 123456 123456 123456
出力例 2
0
条件を満たす組が存在しない場合もあります。
入力例 3
30 8 3 6 4 9 6 5 6 5 6 3 4 7 3 7 4 9 8 5 8 3 6 8 8 4 5 5 5 6 5
出力例 3
17
Score : 300 points
Problem Statement
You are given an integer sequence A=(A _ 1,A _ 2,\ldots,A _ N) of length N.
Find how many pairs of integers (i,j)\ (1\le i\lt j\le N) satisfy j-i=A _ i+A _ j.
Constraints
- 1\le N\le2\times10 ^ 5
- 1\le A _ i\le2\times10 ^ 5\ (1\le i\le N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A _ 1 A _ 2 \ldots A _ N
Output
Output the answer.
Sample Input 1
9 3 1 4 1 5 9 2 6 5
Sample Output 1
3
For example, when (i,j)=(4,7), we have j-i=7-4=3 and A _ i+A _ j=1+2=3, so j-i=A _ i+A _ j.
In contrast, when (i,j)=(3,8), we have j-i=8-3=5 and A _ i+A _ j=4+6=10, so j-i\ne A _ i+A _ j.
Only the three pairs (i,j)=(1,9),(2,4),(4,7) satisfy the condition, so output 3.
Sample Input 2
3 123456 123456 123456
Sample Output 2
0
There may be no pairs that satisfy the condition.
Sample Input 3
30 8 3 6 4 9 6 5 6 5 6 3 4 7 3 7 4 9 8 5 8 3 6 8 8 4 5 5 5 6 5
Sample Output 3
17
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
高橋くんは、これから N 個のプレゼントをもらいます。
高橋くんにはテンションという非負整数のパラメータがあり、テンションはプレゼントをもらうごとに変動します。 それぞれのプレゼントは価値 P 、テンション上げ度 A 、テンション下げ度 B という 3 つのパラメータをもち、これらのパラメータによって高橋くんのテンションは次のように変動します。
- もらったプレゼントの価値 P がテンションの値以上であるとき、高橋くんはプレゼントに喜び、テンションが A だけ増加する。
- もらったプレゼントの価値 P がテンションの値より小さいとき、高橋くんはプレゼントにがっかりし、テンションが B だけ減少する。ただし、高橋くんのテンションの値が B より小さかった場合、高橋くんのテンションは 0 になる。
i 番目 (1\le i\le N) に受け取るプレゼントの価値は P _ i 、テンション上げ度は A _ i 、テンション下げ度は B _ i です。
Q 個の質問が与えられるので、その全てに答えてください。 i 番目 (1\le i\le Q) の質問では、非負整数 X _ i が与えられるので次の質問に答えてください。
高橋くんのテンションがはじめ X _ i だったときの、N 個のプレゼントをすべて受け取ったあとの高橋くんのテンションを求めよ。
制約
- 1\le N\le10000
- 1\le P _ i\le500\ (1\le i\le N)
- 1\le A _ i\le500\ (1\le i\le N)
- 1\le B _ i\le500\ (1\le i\le N)
- 1\le Q\le5\times10 ^ 5
- 0\le X _ i\le10 ^ 9\ (1\le i\le Q)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N P _ 1 A _ 1 B _ 1 P _ 2 A _ 2 B _ 2 \vdots P _ N A _ N B _ N Q X _ 1 X _ 2 \vdots X _ Q
出力
Q 行にわたって出力せよ。 i 行目には、i 番目の質問に対する答えを出力せよ。
入力例 1
4 3 1 4 1 5 9 2 6 5 3 5 8 11 0 1 2 3 4 5 6 7 8 9 10
出力例 1
6 0 0 0 5 6 0 0 0 0 0
高橋くんのテンションがはじめ 10 だったとき、高橋くんのテンションは以下のように変動します。
- 1 つめのプレゼントの価値 3 は高橋くんのテンション 10 未満なので、テンション下げ度 4 だけ高橋くんのテンションが減少し、高橋くんのテンションが 6 になる。
- 2 つめのプレゼントの価値 1 は高橋くんのテンション 6 未満で、高橋くんのテンション 6 はテンション下げ度 9 未満なので、高橋くんのテンションが 0 になる。
- 3 つめのプレゼントの価値 2 は高橋くんのテンション 0 以上なので、テンション上げ度 6 だけ高橋くんのテンションが増加し、高橋くんのテンションが 6 になる。
- 4 つめのプレゼントの価値 3 は高橋くんのテンション 6 未満で、高橋くんのテンション 6 はテンション下げ度 8 未満なので、高橋くんのテンションが 0 になる。
よって、最終的な高橋くんのテンションは 0 になります。
入力例 2
3 500 500 500 500 500 500 500 500 500 1 1000000000
出力例 2
999998500
高橋くんのテンションが高すぎるため、最高のプレゼントを貰っていても高橋くんのテンションは下がり続けます。
入力例 3
20 124 370 105 280 200 420 425 204 302 435 141 334 212 287 231 262 410 481 227 388 466 222 314 366 307 205 401 226 460 452 336 291 119 302 104 432 478 348 292 246 337 403 102 404 371 368 399 417 291 416 351 236 263 231 170 415 482 101 339 184 20 1162 1394 1695 2501 3008 3298 4053 4093 4330 5199 5302 5869 5875 6332 6567 7483 7562 7725 9723 9845
出力例 3
339 339 339 339 339 339 339 339 339 339 339 339 339 389 339 643 722 885 2883 3005
Score : 425 points
Problem Statement
Takahashi will receive N presents.
He has a parameter called mood, which is a non-negative integer, and his mood changes every time he receives a present. Each present has three parameters: value P, mood increase A, and mood decrease B, and his mood changes as follows based on these parameters:
- When the value P of the received present is greater than or equal to his mood, he is happy with the present, and his mood increases by A.
- When the value P of the received present is less than his mood, he is disappointed with the present, and his mood decreases by B. However, if his mood is originally less than B, it becomes 0.
The i-th (1\le i\le N) present he receives has value P _ i, mood increase A _ i, and mood decrease B _ i.
You are given Q questions, so answer all of them. In the i-th (1\le i\le Q) question, you are given a non-negative integer X _ i, so answer the following question:
Find Takahashi's mood after receiving all N presents when his mood is initially X _ i.
Constraints
- 1\le N\le10000
- 1\le P _ i\le500\ (1\le i\le N)
- 1\le A _ i\le500\ (1\le i\le N)
- 1\le B _ i\le500\ (1\le i\le N)
- 1\le Q\le5\times10 ^ 5
- 0\le X _ i\le10 ^ 9\ (1\le i\le Q)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N P _ 1 A _ 1 B _ 1 P _ 2 A _ 2 B _ 2 \vdots P _ N A _ N B _ N Q X _ 1 X _ 2 \vdots X _ Q
Output
Output Q lines. The i-th line should contain the answer to the i-th question.
Sample Input 1
4 3 1 4 1 5 9 2 6 5 3 5 8 11 0 1 2 3 4 5 6 7 8 9 10
Sample Output 1
6 0 0 0 5 6 0 0 0 0 0
When Takahashi's initial mood is 10, his mood changes as follows:
- The value 3 of the first present is less than his mood 10, so his mood decreases by the mood decrease 4, and his mood becomes 6.
- The value 1 of the second present is less than his mood 6, and Takahashi's mood 6 is less than the mood decrease 9, so his mood becomes 0.
- The value 2 of the third present is not less than his mood 0, so his mood increases by the mood increase 6, and his mood becomes 6.
- The value 3 of the fourth present is less than his mood 6, and Takahashi's mood 6 is less than the mood decrease 8, so his mood becomes 0.
Therefore, his final mood is 0.
Sample Input 2
3 500 500 500 500 500 500 500 500 500 1 1000000000
Sample Output 2
999998500
Because Takahashi's mood is too high, his mood keeps decreasing even when he receives the best presents.
Sample Input 3
20 124 370 105 280 200 420 425 204 302 435 141 334 212 287 231 262 410 481 227 388 466 222 314 366 307 205 401 226 460 452 336 291 119 302 104 432 478 348 292 246 337 403 102 404 371 368 399 417 291 416 351 236 263 231 170 415 482 101 339 184 20 1162 1394 1695 2501 3008 3298 4053 4093 4330 5199 5302 5869 5875 6332 6567 7483 7562 7725 9723 9845
Sample Output 3
339 339 339 339 339 339 339 339 339 339 339 339 339 389 339 643 722 885 2883 3005
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 475 点
問題文
N 頂点 M 辺の単純連結無向グラフ G が与えられます。
G の頂点は頂点 1, 頂点 2, \ldots, 頂点 N と番号付けられており、
i (1\leq i\leq M) 本目の辺は頂点 U_i と頂点 V_i を結んでいます。
G における頂点 X から頂点 Y への単純パスのうち辞書順最小のものを求めてください。
すなわち、以下の条件をみたす整数列 P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) の中で辞書順最小のものを求めてください。
- 1\leq P_i\leq N
- i\neq j ならば P_i\neq P_j
- P_1=X かつ P_{\lvert P\rvert}=Y
- 1\leq i\leq \lvert P\rvert-1 について、頂点 P_i と頂点 P_{i+1} を結ぶ辺が存在する。
なお、本問題の制約下で条件をみたすようなものが必ず存在することが証明できます。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
整数列の辞書順 とは
整数列 S=(S_1,S_2,\ldots,S_{\lvert S\rvert}) が整数列 T=(T_1,T_2,\ldots,T_{\lvert T\rvert}) より辞書順で小さいとは、下記の 1. と 2. のどちらかが成り立つことを言います。 ここで、\lvert S\rvert, \lvert T\rvert はそれぞれ S,T の長さを表します。- \lvert S\rvert<\lvert T\rvert かつ (S_1,S_2,\ldots,S_{\lvert S\rvert})=(T_1,T_2,\ldots,T_{\lvert S\rvert})。
- ある 1\leq i\leq \min(\lvert S\rvert,\lvert T\rvert) が存在して (S_1,S_2,\ldots,S_{i-1})=(T_1,T_2,\ldots,T_{i-1}) かつ S_i< T_i。
制約
- 1\leq T\leq 500
- 2\leq N\leq 1000
- N-1\leq M\leq \min\left( \frac{N(N-1)}{2},5\times 10^4\right)
- 1\leq X,Y \leq N
- X\neq Y
- 1\leq U_i<V_i \leq N
- i\neq j ならば (U_i,V_i)\neq (U_j,V_j)
- 与えられるグラフは連結である。
- 1 つの入力における N の総和は 1000 以下である。
- 1 つの入力における M の総和は 5\times 10^4 以下である。
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
\mathrm{case}_i は i 番目のテストケースを表す。 各テストケースは以下の形式で与えられる。
N M X Y U_1 V_1 U_2 V_2 \vdots U_M V_M
出力
T 行出力せよ。
i 行目 (1\leq i\leq T) には、i 個目のテストケースの答えとなる単純パス上の頂点番号を、順に空白区切りで出力せよ。
すなわち i 個目のテストケースに対する答えが P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) であるとき、
P_1, P_2, \ldots, P_{\lvert P\rvert} を i 行目にこの順に空白区切りで出力せよ。
入力例 1
2 6 10 3 5 1 2 1 3 1 5 1 6 2 4 2 5 2 6 3 4 3 5 5 6 3 2 3 2 1 3 2 3
出力例 1
3 1 2 5 3 2
1 つめのテストケースについて、グラフ G は次のようになっています。
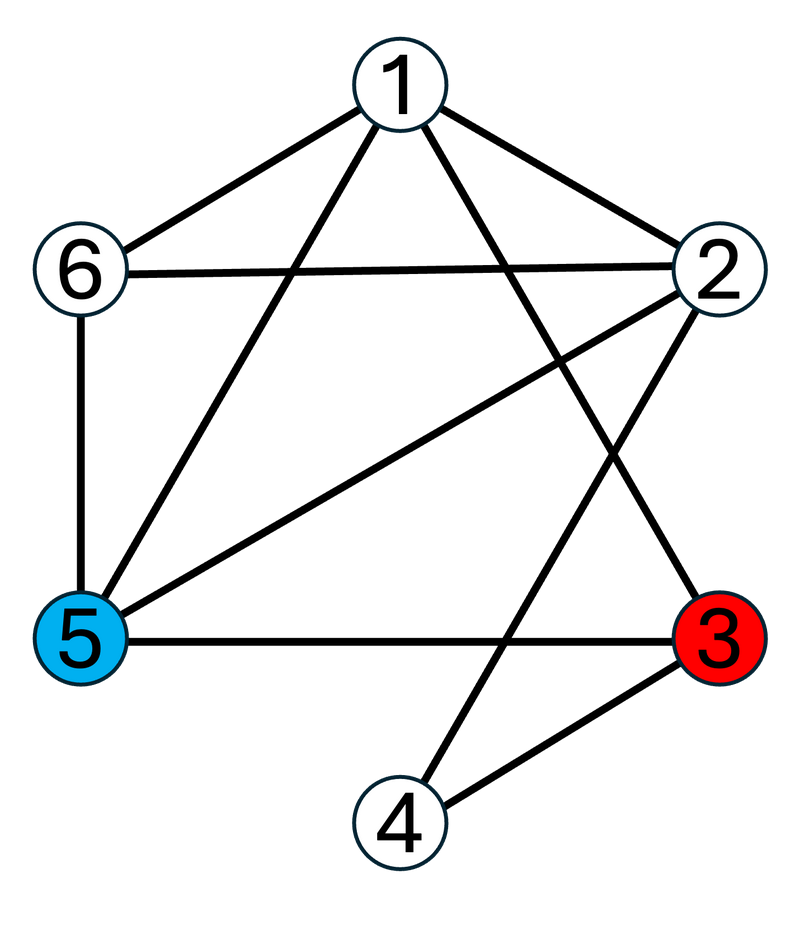
G 上の頂点 3 から頂点 5 への単純パスを辞書順に列挙すると、次のとおりになります。
- (3,1,2,5)
- (3,1,2,6,5)
- (3,1,5)
- (3,1,6,2,5)
- (3,1,6,5)
- (3,4,2,1,5)
- (3,4,2,1,6,5)
- (3,4,2,5)
- (3,4,2,6,1,5)
- (3,4,2,6,5)
- (3,5)
このうち、辞書順最小のものは (3,1,2,5) であるため、1 行目には 3,1,2,5 を空白区切りで出力します。
2 つめのテストケースにおいては、(3,2) が頂点 3 から頂点 2 への唯一の単純パスです。
Score : 475 points
Problem Statement
You are given a simple connected undirected graph G with N vertices and M edges.
The vertices of G are numbered vertex 1, vertex 2, \ldots, vertex N, and
the i-th (1\leq i\leq M) edge connects vertices U_i and V_i.
Find the lexicographically smallest simple path from vertex X to vertex Y in G.
That is, find the lexicographically smallest among the integer sequences P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) that satisfy the following conditions:
- 1\leq P_i\leq N
- If i\neq j, then P_i\neq P_j.
- P_1=X and P_{\lvert P\rvert}=Y.
- For 1\leq i\leq \lvert P\rvert-1, there exists an edge connecting vertices P_i and P_{i+1}.
One can prove that such a path always exists under the constraints of this problem.
You are given T test cases, so find the answer for each.
Lexicographic order on integer sequences
An integer sequence S=(S_1,S_2,\ldots,S_{\lvert S\rvert}) is lexicographically smaller than an integer sequence T=(T_1,T_2,\ldots,T_{\lvert T\rvert}) if either of the following 1. or 2. holds. Here, \lvert S\rvert and \lvert T\rvert represent the lengths of S and T, respectively.- \lvert S\rvert<\lvert T\rvert and (S_1,S_2,\ldots,S_{\lvert S\rvert})=(T_1,T_2,\ldots,T_{\lvert S\rvert}).
- There exists some 1\leq i\leq \min(\lvert S\rvert,\lvert T\rvert) such that (S_1,S_2,\ldots,S_{i-1})=(T_1,T_2,\ldots,T_{i-1}) and S_i< T_i.
Constraints
- 1\leq T\leq 500
- 2\leq N\leq 1000
- N-1\leq M\leq \min\left( \frac{N(N-1)}{2},5\times 10^4\right)
- 1\leq X,Y \leq N
- X\neq Y
- 1\leq U_i<V_i \leq N
- If i\neq j, then (U_i,V_i)\neq (U_j,V_j).
- The given graph is connected.
- The sum of N over all test cases in each input is at most 1000.
- The sum of M over all test cases in each input is at most 5\times 10^4.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
\mathrm{case}_i represents the i-th test case. Each test case is given in the following format:
N M X Y U_1 V_1 U_2 V_2 \vdots U_M V_M
Output
Output T lines.
The i-th line (1\leq i\leq T) should contain the vertex numbers on the simple path that is the answer to the i-th test case, in order, separated by spaces.
That is, when the answer to the i-th test case is P=(P_1,P_2,\ldots,P_{\lvert P\rvert}),
output P_1, P_2, \ldots, P_{\lvert P\rvert} on the i-th line in this order, separated by spaces.
Sample Input 1
2 6 10 3 5 1 2 1 3 1 5 1 6 2 4 2 5 2 6 3 4 3 5 5 6 3 2 3 2 1 3 2 3
Sample Output 1
3 1 2 5 3 2
For the first test case, graph G is as follows:

The simple paths from vertex 3 to vertex 5 on G, listed in lexicographic order, are as follows:
- (3,1,2,5)
- (3,1,2,6,5)
- (3,1,5)
- (3,1,6,2,5)
- (3,1,6,5)
- (3,4,2,1,5)
- (3,4,2,1,6,5)
- (3,4,2,5)
- (3,4,2,6,1,5)
- (3,4,2,6,5)
- (3,5)
Among these, the lexicographically smallest is (3,1,2,5), so output 3,1,2,5 separated by spaces on the first line.
For the second test case, (3,2) is the only simple path from vertex 3 to vertex 2.
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
N 個の皿が、皿 1, 皿 2,\ldots, 皿 N の順に左から並んでいます。 はじめ、皿 i\ (1\le i\le N) には A _ i 個の石が入っています。
この皿たちに対して M 回の操作を行います。 i 回目 (1\le i\le M) の操作では、2 つの整数 L _ i,R _ i が与えられ、次の操作を順に行います。
- 皿 L _ i, 皿 L _ i+1,\ldots, 皿 R _ i の R _ i-L _ i+1 個の皿に入っている石をすべて皿の上から取り除く。
- L _ i 以上 R _ i 以下の整数を一様ランダムに 1 つ取り、それを x とする。
- 取り除いた石をすべて皿 x に乗せる。
i=1,2,\ldots,N について、M 回の操作がすべて終了したときに皿 i に置かれている石の個数の期待値を{}\bmod998244353 で求めてください。
期待値を{}\bmod{998244353} で求めるとは
求める期待値は必ず有理数になることが証明できます。 また、この問題の制約のもとでは、その値を既約分数 \frac{P}{Q} で表した時、Q \not\equiv 0 \pmod{998244353} となることも証明できます。 よって、R \times Q \equiv P \pmod{998244353}, 0 \leq R \lt 998244353 を満たす整数 R が一意に定まります。期待値を{}\bmod{998244353} で求めるとは、この R を求めることを指します。
制約
- 1\le N\le2\times10 ^ 5
- 1\le M\le2\times10 ^ 5
- 0\le A _ i\lt998244353\ (1\le i\le N)
- 1\le L _ i\le R _ i\le N\ (1\le i\le M)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M A _ 1 A _ 2 \ldots A _ N L _ 1 R _ 1 L _ 2 R _ 2 \vdots L _ M R _ M
出力
空白を区切りとして N 個の整数を 1 行に出力せよ。 i 番目 (1\leq i\leq N) には M 回の操作がすべて終了したときに皿 i に置かれている石の個数の期待値を{}\bmod998244353 で求め、出力せよ。
入力例 1
7 4 30 10 40 10 50 90 20 4 6 5 7 1 6 3 7
出力例 1
35 35 36 36 36 36 36
例えば、操作は次のように進みます。
- 1 回目の操作で 4 が選ばれる。皿 1, 皿 2,\ldots, 皿 7 に置かれている石の個数はそれぞれ 30 個 ,10 個 ,40 個 ,150 個 ,0 個 ,0 個 ,20 個となる。
- 2 回目の操作で 6 が選ばれる。皿 1, 皿 2,\ldots, 皿 7 に置かれている石の個数はそれぞれ 30 個 ,10 個 ,40 個 ,150 個 ,0 個 ,20 個 ,0 個となる。
- 3 回目の操作で 2 が選ばれる。皿 1, 皿 2,\ldots, 皿 7 に置かれている石の個数はそれぞれ 0 個 ,250 個 ,0 個 ,0 個 ,0 個 ,0 個 ,0 個となる。
- 4 回目の操作で 3 が選ばれる。皿 1, 皿 2,\ldots, 皿 7 に置かれている石の個数はそれぞれ 0 個 ,250 個 ,0 個 ,0 個 ,0 個 ,0 個 ,0 個となる。
すべての操作が終了したときに皿 1, 皿 2 に置かれている石の個数の期待値は 35 、皿 3, 皿 4, 皿 5, 皿 6, 皿 7に置かれている石の個数の期待値は 36 なので、35 35 36 36 36 36 36 を出力してください。
入力例 2
2 1 0 1 1 2
出力例 2
499122177 499122177
期待値を{}\bmod998244353 で求めることに注意してください。
すべての操作が終了したとき、どちらの皿についても \dfrac12 の確率で石が 1 つ置かれており、\dfrac12 の確率で石が 1 つも置かれていません。
よって、置かれている石の個数の期待値は \dfrac12 です。
499122177\times2\equiv1\pmod{998244353} なので、499122177 499122177 を出力してください。
入力例 3
15 10 61477244 450343304 812961384 836482955 280670539 405068748 318805088 304825858 518212597 316347783 589272551 505875419 944071276 364842194 5376942 2 11 5 9 8 15 6 7 6 8 1 2 1 10 4 9 12 15 6 11
出力例 3
449356308 449356308 449356308 449356308 449356308 648148154 648148154 648148154 648148154 648148154 648148154 643863031 643863031 643863031 643863031
Score : 500 points
Problem Statement
There are N plates arranged from left to right as plate 1, plate 2,\ldots, plate N. Initially, plate i\ (1\le i\le N) contains A _ i stones.
You will perform M operations on these plates. In the i-th operation (1\le i\le M), two integers L _ i and R _ i are given, and the following operations are performed in order:
- Remove all stones from the R _ i-L _ i+1 plates: plate L _ i, plate L _ i+1,\ldots, plate R _ i.
- Uniformly randomly choose an integer between L _ i and R _ i, inclusive, and let it be x.
- Place all the removed stones on plate x.
For i=1,2,\ldots,N, find the expected number, modulo 998244353, of stones placed on plate i when all M operations are completed.
Finding expected value modulo 998244353
It can be proved that the expected value you seek is always a rational number. Also, under the constraints of this problem, when that value is expressed as an irreducible fraction \frac{P}{Q}, it can be proved that Q \not\equiv 0 \pmod{998244353}. Therefore, there is a unique integer R such that R \times Q \equiv P \pmod{998244353}, 0 \leq R \lt 998244353. Finding the expected value modulo 998244353 means finding this R.
Constraints
- 1\le N\le2\times10 ^ 5
- 1\le M\le2\times10 ^ 5
- 0\le A _ i\lt998244353\ (1\le i\le N)
- 1\le L _ i\le R _ i\le N\ (1\le i\le M)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A _ 1 A _ 2 \ldots A _ N L _ 1 R _ 1 L _ 2 R _ 2 \vdots L _ M R _ M
Output
Output N integers separated by spaces on a single line. For the i-th (1\leq i\leq N), find the expected number, modulo 998244353, of stones placed on plate i when all M operations are completed, and output it.
Sample Input 1
7 4 30 10 40 10 50 90 20 4 6 5 7 1 6 3 7
Sample Output 1
35 35 36 36 36 36 36
For example, the operations proceed as follows:
- In the first operation, 4 is chosen. The number of stones on plates 1, 2,\ldots, 7 becomes 30, 10, 40, 150, 0, 0, 20, respectively.
- In the second operation, 6 is chosen. The number of stones on plates 1, 2,\ldots, 7 becomes 30, 10, 40, 150, 0, 20, 0, respectively.
- In the third operation, 2 is chosen. The number of stones on plates 1, 2,\ldots, 7 becomes 0, 250, 0, 0, 0, 0, 0, respectively.
- In the fourth operation, 3 is chosen. The number of stones on plates 1, 2,\ldots, 7 becomes 0, 250, 0, 0, 0, 0, 0, respectively.
When all operations are completed, the expected number of stones on plates 1, 2 is 35, and the expected number of stones on plates 3, 4, 5, 6, 7 is 36, so output 35 35 36 36 36 36 36.
Sample Input 2
2 1 0 1 1 2
Sample Output 2
499122177 499122177
Note that you need to find the expected value modulo 998244353.
When all operations are completed, for both plates, there is a \dfrac12 probability that one stone is placed, and a \dfrac12 probability that no stone is placed.
Therefore, the expected number of stones placed is \dfrac12.
We have 499122177\times2\equiv1\pmod{998244353}, so output 499122177 499122177.
Sample Input 3
15 10 61477244 450343304 812961384 836482955 280670539 405068748 318805088 304825858 518212597 316347783 589272551 505875419 944071276 364842194 5376942 2 11 5 9 8 15 6 7 6 8 1 2 1 10 4 9 12 15 6 11
Sample Output 3
449356308 449356308 449356308 449356308 449356308 648148154 648148154 648148154 648148154 648148154 648148154 643863031 643863031 643863031 643863031
Time Limit: 6 sec / Memory Limit: 1024 MiB
配点 : 625 点
問題文
文字列 S_0,S_1 を S_0= 0, S_1= 1 と定義します。
クエリが Q 個与えられるので、順に処理してください。
i 番目 (1\leq i\leq Q) のクエリでは、3 つの整数の組 (L_i,R_i,X_i) が与えられます。
S_{L_i} と S_{R_i} をこの順に連結した文字列を S_{i+1} とする。 その後、S_{i+1} の X_i 文字目を求める。
なお、X_i が S_{i+1} の長さ以下であることは保証される。
制約
- 1\leq Q\leq 5\times 10^5
- 0\leq L_i,R_i\leq i
- 1\leq X_i\leq 10^{18}
- X_i は S_{i+1} の長さ以下である。
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
Q L_1 R_1 X_1 L_2 R_2 X_2 \vdots L_Q R_Q X_Q
出力
Q 行出力せよ。 i 行目 (1\leq i\leq Q) には、i 番目のクエリに対する答えを出力せよ。
入力例 1
7 0 1 1 0 0 2 1 1 1 2 3 2 2 4 3 5 4 2 6 7 6
出力例 1
0 0 1 1 1 1 1
各クエリは次のように処理されます。
- 1 番目のクエリでは S_0=
0と S_1=1を連結し、S_2=01となります。S_2 の 1 文字目は0であるため、1 行目には 0 を出力します。 - 2 番目のクエリでは S_0=
0と S_0=0を連結し、S_3=00となります。S_3 の 2 文字目は0であるため、2 行目には 0 を出力します。 - 3 番目のクエリでは S_1=
1と S_1=1を連結し、S_4=11となります。S_4 の 1 文字目は1であるため、3 行目には 1 を出力します。 - 4 番目のクエリでは S_2=
01と S_3=00を連結し、S_5=0100となります。S_5 の 2 文字目は1であるため、4 行目には 1 を出力します。 - 5 番目のクエリでは S_2=
01と S_4=11を連結し、S_6=0111となります。S_6 の 3 文字目は1であるため、5 行目には 1 を出力します。 - 6 番目のクエリでは S_5=
0100と S_4=11を連結し、S_7=010011となります。S_7 の 2 文字目は1であるため、6 行目には 1 を出力します。 - 7 番目のクエリでは S_6=
0111と S_7=010011を連結し、S_8=0111010011となります。S_8 の 6 文字目は1であるため、7 行目には 1 を出力します。
Score : 625 points
Problem Statement
Define strings S_0 and S_1 as S_0= 0 and S_1= 1.
You are given Q queries, so process them in order.
In the i-th query (1\leq i\leq Q), you are given a triple of integers (L_i,R_i,X_i).
Let S_{i+1} be the string obtained by concatenating S_{L_i} and S_{R_i} in this order. Then, find the X_i-th character of S_{i+1}.
It is guaranteed that X_i is at most the length of S_{i+1}.
Constraints
- 1\leq Q\leq 5\times 10^5
- 0\leq L_i,R_i\leq i
- 1\leq X_i\leq 10^{18}
- X_i is at most the length of S_{i+1}.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
Q L_1 R_1 X_1 L_2 R_2 X_2 \vdots L_Q R_Q X_Q
Output
Output Q lines. The i-th line (1\leq i\leq Q) should contain the answer to the i-th query.
Sample Input 1
7 0 1 1 0 0 2 1 1 1 2 3 2 2 4 3 5 4 2 6 7 6
Sample Output 1
0 0 1 1 1 1 1
Each query is processed as follows:
- In the first query, concatenate S_0=
0and S_1=1to get S_2=01. The first character of S_2 is0, so output 0 on the first line. - In the second query, concatenate S_0=
0and S_0=0to get S_3=00. The second character of S_3 is0, so output 0 on the second line. - In the third query, concatenate S_1=
1and S_1=1to get S_4=11. The first character of S_4 is1, so output 1 on the third line. - In the fourth query, concatenate S_2=
01and S_3=00to get S_5=0100. The second character of S_5 is1, so output 1 on the fourth line. - In the fifth query, concatenate S_2=
01and S_4=11to get S_6=0111. The third character of S_6 is1, so output 1 on the fifth line. - In the sixth query, concatenate S_5=
0100and S_4=11to get S_7=010011. The second character of S_7 is1, so output 1 on the sixth line. - In the seventh query, concatenate S_6=
0111and S_7=010011to get S_8=0111010011. The sixth character of S_8 is1, so output 1 on the seventh line.