Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
高橋くんは、N 個の品物と 1 つのカバンを持っています。
i 番目 (1\le i\le N) の品物の大きさは A _ i で、カバンの大きさは M です。
カバンに入れようとしている品物の大きさの合計が M 以下のとき、かつそのときに限り、それらの品物をすべて同時にカバンに入れることができます。
高橋くんが N 個の品物すべてを同時にカバンに入れることができるなら Yes 、そうでなければ No と出力してください。
制約
- 1\le N\le100
- 1\le M\le10000
- 1\le A _ i\le100\ (1\le i\le N)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M A _ 1 A _ 2 \ldots A _ N
出力
高橋くんがすべての品物を同時にカバンに入れられるなら Yes を、そうでなければ No を出力せよ。
入力例 1
5 15 3 1 4 1 5
出力例 1
Yes
5 つの品物の大きさの合計は 3+1+4+1+5=14 です。
これは、カバンの大きさ 15 以下なので、高橋くんはすべての品物を同時にカバンに入れることができます。
なので、Yes を出力してください。
入力例 2
5 5 3 1 4 1 5
出力例 2
No
5 つの品物の大きさの合計は 14 で、カバンの大きさ 5 より大きいため、高橋くんはすべての品物を同時にカバンに入れることができません。
なので、No を出力してください。
入力例 3
1 10000 100
出力例 3
Yes
Score : 100 points
Problem Statement
Takahashi has N items and one bag.
The size of the i-th (1\le i\le N) item is A_i, and the size of the bag is M.
If and only if the total size of the items he is trying to put in the bag is at most M, he can put all those items in the bag simultaneously.
If he can put all N items in the bag simultaneously, print Yes; otherwise, print No.
Constraints
- 1\le N\le100
- 1\le M\le10000
- 1\le A_i\le100\ (1\le i\le N)
- All input values are integers.
Input
The input is given from standard input in the following format:
N M A_1 A_2 \ldots A_N
Output
If Takahashi can put all items in the bag simultaneously, print Yes; otherwise, print No.
Sample Input 1
5 15 3 1 4 1 5
Sample Output 1
Yes
The total size of the 5 items is 3+1+4+1+5=14.
Since this is not greater than the bag size 15, Takahashi can put all items in the bag simultaneously.
Thus, print Yes.
Sample Input 2
5 5 3 1 4 1 5
Sample Output 2
No
The total size of the 5 items is 14, which is greater than the bag size 5, so he cannot put all items in the bag simultaneously.
Thus, print No.
Sample Input 3
1 10000 100
Sample Output 3
Yes
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
N 種類の文字列 S _ 1,S _ 2,\ldots,S _ N が与えられます。
あなたは、次の操作を 1 度だけ行います。
- 相異なる整数 i,j\ (1\le i\le N,1\le j\le N) を選び、S _ i と S _ j をこの順で連結する。
この操作で連結した結果の文字列としてありえるものは何通りあるか求めてください。
選んだ (i,j) が異なっても、連結した文字列が同じ場合は 1 通りと数えることに注意してください。
制約
- 2\le N\le100
- N は整数
- S _ i は英小文字からなる長さ 1 以上 10 以下の文字列
- S _ i\ne S _ j\ (1\le i\lt j\le N)
入力
入力は以下の形式で標準入力から与えられる。
N S _ 1 S _ 2 \vdots S _ N
出力
操作の結果できる文字列が何通りあるかを出力せよ。
入力例 1
4 at atco coder der
出力例 1
11
できる文字列は、atatco, atcoat, atcoder, atcocoder, atder, coderat, coderatco, coderder, derat, deratco, dercoder の 11 通りです。
よって、11 を出力してください。
入力例 2
5 a aa aaa aaaa aaaaa
出力例 2
7
できる文字列は、aaa, aaaa, aaaaa, aaaaaa, aaaaaaa, aaaaaaaa, aaaaaaaaa の 7 通りです。
よって、7 を出力してください。
入力例 3
10 armiearggc ukupaunpiy cogzmjmiob rtwbvmtruq qapfzsitbl vhkihnipny ybonzypnsn esxvgoudra usngxmaqpt yfseonwhgp
出力例 3
90
Score : 200 points
Problem Statement
You are given N types of strings S_1,S_2,\ldots,S_N.
You perform the following operation once:
- Choose distinct integers i and j\ (1\le i\le N,1\le j\le N) and concatenate S_i and S_j in this order.
How many different strings can be obtained as a result of this operation?
If different choices of (i,j) result in the same concatenated string, it is counted as one string.
Constraints
- 2\le N\le100
- N is an integer.
- S_i is a string of length between 1 and 10, inclusive, consisting of lowercase English letters.
- S_i\ne S_j\ (1\le i\lt j\le N)
Input
The input is given from standard input in the following format:
N S_1 S_2 \vdots S_N
Output
Print the number of different strings that can be obtained from the operation.
Sample Input 1
4 at atco coder der
Sample Output 1
11
The possible strings are atatco, atcoat, atcoder, atcocoder, atder, coderat, coderatco, coderder, derat, deratco, dercoder, which are 11 strings.
Thus, print 11.
Sample Input 2
5 a aa aaa aaaa aaaaa
Sample Output 2
7
The possible strings are aaa, aaaa, aaaaa, aaaaaa, aaaaaaa, aaaaaaaa, aaaaaaaaa, which are 7 strings.
Thus, print 7.
Sample Input 3
10 armiearggc ukupaunpiy cogzmjmiob rtwbvmtruq qapfzsitbl vhkihnipny ybonzypnsn esxvgoudra usngxmaqpt yfseonwhgp
Sample Output 3
90
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
空の整数列 A=() があります。クエリが Q 個与えられるので、与えられた順に処理してください。クエリは以下の 2 種類です。
- タイプ 1 :
1 c xの形式で与えられる。A の末尾に x を c 個追加する。 - タイプ 2 :
2 kの形式で与えられる。A の先頭 k 要素を削除し、削除した k 個の整数の総和を出力する。このとき、k はその時点での A の長さ以下であることが保証される。
制約
- 1 \leq Q \leq 2 \times 10^{5}
- タイプ 1 のクエリにおいて、 1 \leq c \leq 10^{9}
- タイプ 1 のクエリにおいて、 1 \leq x \leq 10^{9}
- タイプ 2 のクエリにおいて、その時点での A の長さを n として、 1 \leq k \leq \min(10^{9},n)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
ただし、 \text{query}_i は i 個目のクエリを表し、以下のいずれかの形式である。
1 c x
2 k
出力
タイプ 2 のクエリの個数を q として、q 行出力せよ。i 行目には、i 個目のタイプ 2 のクエリに対する答えを出力せよ。
入力例 1
5 1 2 3 1 4 5 2 3 1 6 2 2 5
出力例 1
11 19
- 1 個目のクエリ: A の末尾に 3 を 2 個追加する。このとき、A=(3,3) となる。
- 2 個目のクエリ: A の末尾に 5 を 4 個追加する。このとき、A=(3,3,5,5,5,5) となる。
- 3 個目のクエリ: A の先頭 3 要素を削除する。このとき、削除した 3 個の整数の総和は 3+3+5=11 となるため 11 と出力する。削除後、A=(5,5,5) となる。
- 4 個目のクエリ: A の末尾に 2 を 6 個追加する。このとき、A=(5,5,5,2,2,2,2,2,2) となる。
- 5 個目のクエリ: A の先頭 5 要素を削除する。このとき、削除した 5 個の整数の総和は 5+5+5+2+2=19 となるため 19 と出力する。削除後、A=(2,2,2,2) となる。
入力例 2
10 1 75 22 1 81 72 1 2 97 1 84 82 1 2 32 1 39 57 2 45 1 40 16 2 32 2 42
出力例 2
990 804 3024
入力例 3
10 1 160449218 954291757 2 17217760 1 353195922 501899080 1 350034067 910748511 1 824284691 470338674 2 180999835 1 131381221 677959980 1 346948152 208032501 1 893229302 506147731 2 298309896
出力例 3
16430766442004320 155640513381884866 149721462357295680
Score : 300 points
Problem Statement
There is an empty integer sequence A=(). You are given Q queries, and you need to process them in the given order. There are two types of queries:
- Type 1: Given in the format
1 c x. Add c copies of x to the end of A. - Type 2: Given in the format
2 k. Remove the first k elements from A and output the sum of the removed k integers. It is guaranteed that k is at most the length of A at that time.
Constraints
- 1 \leq Q \leq 2 \times 10^{5}
- In type 1 queries, 1 \leq c \leq 10^{9}.
- In type 1 queries, 1 \leq x \leq 10^{9}.
- In type 2 queries, letting n be the length of A at that time, 1 \leq k \leq \min(10^{9},n).
- All input values are integers.
Input
The input is given from standard input in the following format:
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
where \text{query}_i represents the i-th query and is in one of the following formats:
1 c x
2 k
Output
Let q be the number of type 2 queries. Output q lines. The i-th line should contain the answer to the i-th type 2 query.
Sample Input 1
5 1 2 3 1 4 5 2 3 1 6 2 2 5
Sample Output 1
11 19
- 1st query: Add 2 copies of 3 to the end of A. Then, A=(3,3).
- 2nd query: Add 4 copies of 5 to the end of A. Then, A=(3,3,5,5,5,5).
- 3rd query: Remove the first 3 elements from A. Then, the sum of the removed 3 integers is 3+3+5=11, so output 11. After removal, A=(5,5,5).
- 4th query: Add 6 copies of 2 to the end of A. Then, A=(5,5,5,2,2,2,2,2,2).
- 5th query: Remove the first 5 elements from A. Then, the sum of the removed 5 integers is 5+5+5+2+2=19, so output 19. After removal, A=(2,2,2,2).
Sample Input 2
10 1 75 22 1 81 72 1 2 97 1 84 82 1 2 32 1 39 57 2 45 1 40 16 2 32 2 42
Sample Output 2
990 804 3024
Sample Input 3
10 1 160449218 954291757 2 17217760 1 353195922 501899080 1 350034067 910748511 1 824284691 470338674 2 180999835 1 131381221 677959980 1 346948152 208032501 1 893229302 506147731 2 298309896
Sample Output 3
16430766442004320 155640513381884866 149721462357295680
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
長さ N の整数列 A=(A _ 1,A _ 2,\ldots,A _ N) が与えられます。 ここで、どの i\ (1\le i\le N) についても A _ i が 0 でないことが保証されます。
A を適切に並べ替えた数列 B=(B _ 1,B _ 2,\ldots,B _ N) が等比数列になることがあるか判定してください。
ただし、数列 S=(S _ 1,S _ 2,\ldots,S _ N) が等比数列であるとは、ある実数 r が存在してすべての整数 1\le i\lt N に対して S _ {i+1}=rS _ i が成り立つことをいいます。
1 つの入力ファイルにつき、T 個のテストケースを解いてください。
制約
- 1\le T\le10 ^ 5
- 2\le N\le2\times10 ^ 5
- -10 ^ 9\le A _ i\le10 ^ 9\ (1\le i\le N)
- A _ i\ne0\ (1\le i\le N)
- 1 つの入力ファイルにおける N の総和は 2\times10 ^ 5 以下
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{testcase} _ 1
\mathrm{testcase} _ 2
\vdots
\mathrm{testcase} _ T
ここで、\mathrm{testcase} _ i は i 番目 (1\le i\le T) のテストケースであり、各テストケースは以下の形式で与えられる。
N A _ 1 A _ 2 \ldots A _ N
出力
T 行にわたって出力せよ。
i 行目 (1\le i\le T) には、i 番目のテストケースにおいて A を並べ替えて等比数列にできる場合は Yes を、そうでない場合は No を出力せよ。
入力例 1
3 5 1 8 2 4 16 5 -16 24 54 81 -36 7 90000 8100 -27000 729 -300000 -2430 1000000
出力例 1
Yes No Yes
1 つめのテストケースでは、A を並べ替えた (16,8,4,2,1) は、公比 r=\dfrac12 の等比数列になります。
よって、1 行目には Yes と出力してください。
2 つめのテストケースでは、A をどのように並べ替えても条件を満たしません。
よって、2 行目には No と出力してください。
Score : 425 points
Problem Statement
You are given an integer sequence A=(A_1,A_2,\ldots,A_N) of length N. It is guaranteed that for any i\ (1\le i\le N), A_i is not 0.
Determine whether there exists a permutation B=(B_1,B_2,\ldots,B_N) of A such that B forms a geometric sequence.
A sequence S=(S_1,S_2,\ldots,S_N) is a geometric sequence if there exists a real number r such that S_{i+1}=rS_i for all integers 1\le i\lt N.
Solve T test cases per input file.
Constraints
- 1\le T\le10^5
- 2\le N\le2\times10^5
- -10^9\le A_i\le10^9\ (1\le i\le N)
- A_i\ne0\ (1\le i\le N)
- The sum of N over all test cases in a single input file is at most 2\times10^5.
- All input values are integers.
Input
The input is given from standard input in the following format:
T
\mathrm{testcase}_1
\mathrm{testcase}_2
\vdots
\mathrm{testcase}_T
where \mathrm{testcase}_i is the i-th test case (1\le i\le T), and each test case is given in the following format:
N A_1 A_2 \ldots A_N
Output
Output T lines.
The i-th line (1\le i\le T) should contain Yes if A can be rearranged to form a geometric sequence in the i-th test case, and No otherwise.
Sample Input 1
3 5 1 8 2 4 16 5 -16 24 54 81 -36 7 90000 8100 -27000 729 -300000 -2430 1000000
Sample Output 1
Yes No Yes
In the first test case, the rearrangement (16,8,4,2,1) of A forms a geometric sequence with common ratio r=\frac{1}{2}.
Thus, print Yes on the first line.
In the second test case, no rearrangement of A satisfies the condition.
Thus, print No on the second line.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 450 点
問題文
(1,2,3,\ldots,2^{N}) の順列 P=(P_0,P_1,\ldots,P_{2^{N}-1}) が与えられます。
あなたは次の操作を何回でも(0 回でもよい)行うことができます。
- 0 \leq a \times 2^{b} < (a+1) \times 2^{b} \leq 2^{N} を満たす非負整数 a,b を選び、P_{a \times 2^{b}}, P_{a\times 2^{b}+1},\ldots,P_{(a+1) \times 2^{b}-1} を反転する。ここで、P_{a \times 2^{b}},P_{a \times 2^{b}+1},\ldots,P_{(a+1) \times 2^{b}-1} を反転するとは、P_{a \times 2^{b}}, P_{a\times 2^{b}+1},\ldots,P_{(a+1) \times 2^{b}-1} を P_{(a+1) \times 2^{b}-1}, P_{(a+1) \times 2^{b}-2},\ldots,P_{a \times 2^{b}} に同時に置き換えることを意味する。
操作を繰り返して得られる P のうち、辞書順最小のものを求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1 \leq T \leq 10^{5}
- 1 \leq N \leq 18
- P は (1,2,3,\ldots,2^{N}) の順列
- 各入力ファイルについて、すべてのテストケースの 2^N の総和は 3 \times 10^{5} 以下
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T
\textrm{case}_1
\textrm{case}_2
\vdots
\textrm{case}_T
\textrm{case}_i は i 番目のテストケースを表し、以下の形式で与えられる。
N
P_0 P_1 \ldots P_{2^N-1}
出力
T 行出力せよ。i 行目 (1 \leq i \leq T) には i 番目のテストケースに対する答えを出力せよ。
入力例 1
4 1 1 2 2 1 3 4 2 2 2 3 4 1 3 8 3 4 2 1 5 7 6
出力例 1
1 2 1 3 2 4 1 4 2 3 1 5 6 7 2 4 3 8
1 番目のテストケースにおいて、P に対して操作を一回も行わないとき、P=(1,2) となります。これは辞書順で最小の順列です。よって答えは(1,2) です。
2 番目のテストケースにおいて、a=1,b=1 を選んで操作を行うと P=(1,3,2,4) となります。P に対して何回操作を行っても (1,3,2,4) より辞書順で小さい順列を得られません。よって答えは (1,3,2,4) です。
3 番目のテストケースにおいて、以下の順番で操作を行うことで、P=(1,4,2,3) が得られます。
- a=0,b=1 を選んで操作を行う。P=(3,2,4,1) となる。
- a=0,b=2 を選んで操作を行う。P=(1,4,2,3) となる。
P に対して何回操作を行っても (1,4,2,3) より辞書順で小さい順列を得られません。よって答えは (1,4,2,3) です。
Score : 450 points
Problem Statement
You are given a permutation P=(P_0,P_1,\ldots,P_{2^{N}-1}) of (1,2,3,\ldots,2^{N}).
You can perform the following operation any number of times (possibly zero):
- Choose non-negative integers a,b satisfying 0 \leq a \times 2^{b} < (a+1) \times 2^{b} \leq 2^{N}, and reverse P_{a \times 2^{b}}, P_{a\times 2^{b}+1},\ldots,P_{(a+1) \times 2^{b}-1}. Here, reversing P_{a \times 2^{b}}, P_{a\times 2^{b}+1},\ldots,P_{(a+1) \times 2^{b}-1} means simultaneously replacing P_{a \times 2^{b}}, P_{a\times 2^{b}+1},\ldots,P_{(a+1) \times 2^{b}-1} with P_{(a+1) \times 2^{b}-1}, P_{(a+1) \times 2^{b}-2},\ldots,P_{a \times 2^{b}}.
Find the lexicographically smallest permutation P that can be obtained by repeating the operation.
You are given T test cases, so find the answer for each.
Constraints
- 1 \leq T \leq 10^{5}
- 1 \leq N \leq 18
- P is a permutation of (1,2,3,\ldots,2^{N}).
- For each input file, the sum of 2^N over all test cases is at most 3 \times 10^{5}.
- All input values are integers.
Input
The input is given from standard input in the following format:
T
\textrm{case}_1
\textrm{case}_2
\vdots
\textrm{case}_T
\textrm{case}_i represents the i-th test case and is given in the following format:
N
P_0 P_1 \ldots P_{2^N-1}
Output
Output T lines. The i-th line (1 \leq i \leq T) should contain the answer to the i-th test case.
Sample Input 1
4 1 1 2 2 1 3 4 2 2 2 3 4 1 3 8 3 4 2 1 5 7 6
Sample Output 1
1 2 1 3 2 4 1 4 2 3 1 5 6 7 2 4 3 8
In the first test case, when no operation is performed on P, P=(1,2). This is the lexicographically smallest permutation. Thus, the answer is (1,2).
In the second test case, when we perform the operation with a=1,b=1, P becomes (1,3,2,4). No matter how many operations we perform on P, we cannot obtain a permutation lexicographically smaller than (1,3,2,4). Thus, the answer is (1,3,2,4).
In the third test case, by performing operations in the following order, we can obtain P=(1,4,2,3):
- Perform the operation with a=0,b=1. P becomes (3,2,4,1).
- Perform the operation with a=0,b=2. P becomes (1,4,2,3).
No matter how many operations we perform on P, we cannot obtain a permutation lexicographically smaller than (1,4,2,3). Thus, the answer is (1,4,2,3).
Time Limit: 2.5 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
H 行 W 列のグリッドがあります。上から i 行目、左から j 列目のマスを (i,j) と表します。また、このうち K 個のマスはゴールになっています。i 個目 (1 \leq i \leq K) のゴールはマス (R_i, C_i) です。
高橋君と青木君はこのグリッドとグリッドの上に置かれた 1 つのコマを使ってあるゲームをしています。高橋君と青木君はコマがゴールのマスに到達するまで以下の一連の操作を繰り返し行います。
- 青木君は 1 以上 4 以下の整数 a を選ぶ。
- その後、高橋君は 1 以上 4 以下の整数 b を選ぶ。ただし、a \neq b を満たす必要がある。操作前にコマが置いてあるマスを (i,j) としたとき、選んだ整数 b とコマの位置に応じて以下の通りにコマを移動させる。
- b=1 のとき: マス (i-1,j) がグリッド内である場合はコマをマス (i,j) からマス (i-1,j) に移動させ、グリッドの外である場合はコマを移動させない。
- b=2 のとき: マス (i+1,j) がグリッド内である場合はコマをマス (i,j) からマス (i+1,j) に移動させ、グリッドの外である場合はコマを移動させない。
- b=3 のとき: マス (i,j-1) がグリッド内である場合はコマをマス (i,j) からマス (i,j-1) に移動させ、グリッドの外である場合はコマを移動させない。
- b=4 のとき: マス (i,j+1) がグリッド内である場合はコマをマス (i,j) からマス (i,j+1) に移動させ、グリッドの外である場合はコマを移動させない。
高橋君の目的はコマがゴールに到達するまでの移動回数を最小化することです。青木君の目的はコマがゴールに到達しないようにすることであり、それが不可能な場合は移動回数を最大化することです。
1 \leq i \leq H,1 \leq j \leq W を満たすすべての整数の組 (i,j) に対して以下の問題を解き、解の総和を求めてください。
コマがマス (i,j) にある状態からゲームを始める。両者が各々の目的を目指して最適に行動するとき、高橋君がコマをゴールに到達させることができるのであれば移動回数の最小値、そうでないならば 0 が解である。
制約
- 2 \leq H \leq 3000
- 2 \leq W \leq 3000
- 1 \leq K \leq \min(HW,3000)
- 1 \leq R_i \leq H
- 1 \leq C_i \leq W
- (R_i,C_i) \neq (R_j,C_j) (1 \leq i < j \leq K)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H W K R_1 C_1 R_2 C_2 \vdots R_K C_K
出力
答えを出力せよ。
入力例 1
2 3 2 1 2 2 1
出力例 1
2
(i,j)=(1,2),(2,1) のとき、開始するマスがゴールであるため、解は 0 です。
(i,j)=(1,1),(2,2) のとき、どの a を青木君が選んでも高橋君は 1 回の移動でコマをゴールに到達させることができるため、解は 1 です。
(i,j)=(1,3),(2,3) のとき、高橋君はコマをゴールに到達させることができないため、解は 0 です。
これらの合計は 0 \times 2 + 1 \times 2 + 0 \times 2 = 2 です。よって 2 を出力します。
入力例 2
9 3 9 1 3 6 1 4 1 1 2 2 1 7 1 9 3 8 1 9 2
出力例 2
43
入力例 3
10 10 36 3 8 5 10 3 10 6 10 2 10 2 8 7 10 1 10 1 8 7 6 7 8 2 5 1 6 8 8 7 5 2 4 9 8 7 4 4 3 10 10 10 8 8 10 10 6 6 2 4 2 10 5 8 3 1 2 2 1 4 1 10 4 10 3 8 1 6 1 10 2 9 1
出力例 3
153
Score : 525 points
Problem Statement
There is an H \times W grid. Let (i,j) denote the cell at the i-th row from the top and j-th column from the left. Among these, K cells are goals. The i-th goal (1 \leq i \leq K) is cell (R_i, C_i).
Takahashi and Aoki play a game using this grid and a single piece placed on the grid. Takahashi and Aoki repeatedly perform the following series of operations until the piece reaches a goal cell:
- Aoki chooses an integer a between 1 and 4, inclusive.
- Then, Takahashi chooses an integer b between 1 and 4, inclusive, where a \neq b must be satisfied. Let (i,j) be the cell where the piece is placed before the operation. Based on the chosen integer b and the piece's position, move the piece.
- When b=1: If (i-1,j) is within the grid, move the piece from cell (i,j) to cell (i-1,j); if it is outside the grid, do nothing.
- When b=2: If (i+1,j) is within the grid, move the piece from cell (i,j) to cell (i+1,j); if it is outside the grid, do nothing.
- When b=3: If (i,j-1) is within the grid, move the piece from cell (i,j) to cell (i,j-1); if it is outside the grid, do nothing.
- When b=4: If (i,j+1) is within the grid, move the piece from cell (i,j) to cell (i,j+1); if it is outside the grid, do nothing.
Takahashi's objective is to minimize the number of moves until the piece reaches a goal. Aoki's objective is to prevent the piece from reaching the goal; if that is impossible, his objective is to maximize the number of moves until the piece reaches a goal.
For all pairs of integers (i,j) satisfying 1 \leq i \leq H,1 \leq j \leq W, solve the following problem and find the sum of all solutions:
Start the game with the piece at cell (i,j). Assume both players act optimally toward their respective objectives. If Takahashi can make the piece reach a goal, the solution is the minimum number of moves; otherwise, the solution is 0.
Constraints
- 2 \leq H \leq 3000
- 2 \leq W \leq 3000
- 1 \leq K \leq \min(HW,3000)
- 1 \leq R_i \leq H
- 1 \leq C_i \leq W
- (R_i,C_i) \neq (R_j,C_j) (1 \leq i < j \leq K)
- All input values are integers.
Input
The input is given from standard input in the following format:
H W K R_1 C_1 R_2 C_2 \vdots R_K C_K
Output
Print the answer.
Sample Input 1
2 3 2 1 2 2 1
Sample Output 1
2
When (i,j)=(1,2),(2,1), the starting cell is a goal, so the solution is 0.
When (i,j)=(1,1),(2,2), no matter which a Aoki chooses, Takahashi can make the piece reach a goal in 1 move from the starting cell, so the solution is 1.
When (i,j)=(1,3),(2,3), Takahashi cannot reach a goal, so the solution is 0.
The sum of these is 0 \times 2 + 1 \times 2 + 0 \times 2 = 2. Thus, print 2.
Sample Input 2
9 3 9 1 3 6 1 4 1 1 2 2 1 7 1 9 3 8 1 9 2
Sample Output 2
43
Sample Input 3
10 10 36 3 8 5 10 3 10 6 10 2 10 2 8 7 10 1 10 1 8 7 6 7 8 2 5 1 6 8 8 7 5 2 4 9 8 7 4 4 3 10 10 10 8 8 10 10 6 6 2 4 2 10 5 8 3 1 2 2 1 4 1 10 4 10 3 8 1 6 1 10 2 9 1
Sample Output 3
153
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 575 点
問題文
H 行 W 列のマス目があります。 上から i 行目 (1\le i\le H) 、左から j 行目 (1\le j\le W) のマスをマス (i,j) と呼ぶことにします。
マス目は障害物が置かれているか何も置かれていないかのいずれかで、障害物が置かれているマスはマス (r _ 1,c _ 1),(r _ 2,c _ 2),\ldots,(r _ K,c _ K) の K 個です。
高橋くんははじめマス (1,1) におり、上下左右に隣接する何も置かれていないマスに移動することを繰り返してマス (H,W) へ行きたいと思っています。
厳密には、高橋くんは以下の操作を好きなだけ繰り返すことができます。
- 次の 4 つの操作から 1 つを選び、選んだ操作を行う。
- 1\lt i かつマス (i-1,j) に何も置かれていないならマス (i-1,j) に移動する。そうでなければ移動しない。
- 1\lt j かつマス (i,j-1) に何も置かれていないならマス (i,j-1) に移動する。そうでなければ移動しない。
- i\lt H かつマス (i+1,j) に何も置かれていないならマス (i+1,j) に移動する。そうでなければ移動しない。
- j\lt W かつマス (i,j+1) に何も置かれていないならマス (i,j+1) に移動する。そうでなければ移動しない。
高橋くんがマス (1,1) からマス (H,W) へ移動できるか判定してください。
制約
- 1\le H\le2\times10 ^ 5
- 1\le W\le2\times10 ^ 5
- 0\le K\le2\times10 ^ 5
- 1\le r _ i\le H\ (1\le i\le K)
- 1\le c _ i\le W\ (1\le i\le K)
- (r _ i,c _ i)\ne(1,1)\ (1\le i\le K)
- (r _ i,c _ i)\ne(H,W)\ (1\le i\le K)
- (r _ i,c _ i)\ne(r _ j,c _ j)\ (1\le i\lt j\le K)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H W K r _ 1 c _ 1 r _ 2 c _ 2 \vdots r _ K c _ K
出力
高橋くんが問題文中の操作を繰り返してマス (1,1) からマス (H,W) へ移動することができるなら Yes を、そうでなければ No を出力してください。
入力例 1
4 5 5 1 4 2 3 3 2 3 4 4 2
出力例 1
No
マス目は以下のようになっています。

高橋くんはマス (1,1) からマス (4,5) まで移動することはできません。
入力例 2
2 7 3 1 2 2 4 1 6
出力例 2
Yes
マス目は以下のようになっています。
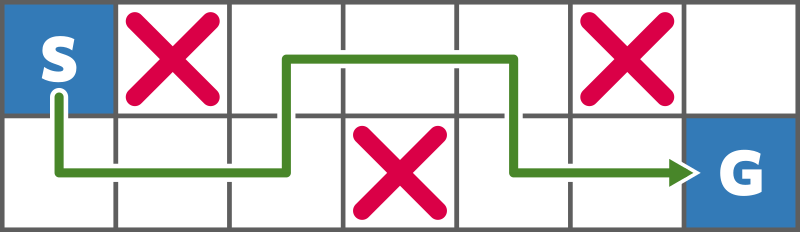
高橋くんは図のように移動することでマス (1,1) からマス (2,7) まで移動することができます。
入力例 3
1 1 0
出力例 3
Yes
高橋くんが移動しなくていい場合や、障害物がひとつも置かれていない場合があることに注意してください。
入力例 4
10 12 20 8 3 1 11 6 4 3 7 10 4 5 7 4 7 5 5 4 3 6 1 1 6 2 7 6 7 1 3 6 3 2 12 9 6 7 3 3 11 9 7
出力例 4
Yes
Score : 575 points
Problem Statement
There is an H \times W grid. Let (i,j) denote the cell at the i-th row (1\le i\le H) from the top and j-th column (1\le j\le W) from the left.
Each cell in the grid either has an obstacle placed on it or has nothing placed on it. There are K cells with obstacles: cells (r_1,c_1),(r_2,c_2),\ldots,(r_K,c_K).
Takahashi is initially at cell (1,1) and wants to reach cell (H,W) by repeatedly moving to an adjacent cell (up, down, left, right) that has nothing placed on it.
More precisely, he can repeat the following operation as many times as he likes:
- Choose one of the following four operations and perform the chosen operation:
- If 1\lt i and cell (i-1,j) has nothing placed on it, move to cell (i-1,j). Otherwise, do not move.
- If 1\lt j and cell (i,j-1) has nothing placed on it, move to cell (i,j-1). Otherwise, do not move.
- If i\lt H and cell (i+1,j) has nothing placed on it, move to cell (i+1,j). Otherwise, do not move.
- If j\lt W and cell (i,j+1) has nothing placed on it, move to cell (i,j+1). Otherwise, do not move.
Determine whether he can move from cell (1,1) to cell (H,W).
Constraints
- 1\le H\le2\times10^5
- 1\le W\le2\times10^5
- 0\le K\le2\times10^5
- 1\le r_i\le H\ (1\le i\le K)
- 1\le c_i\le W\ (1\le i\le K)
- (r_i,c_i)\ne(1,1)\ (1\le i\le K)
- (r_i,c_i)\ne(H,W)\ (1\le i\le K)
- (r_i,c_i)\ne(r_j,c_j)\ (1\le i\lt j\le K)
- All input values are integers.
Input
The input is given from standard input in the following format:
H W K r_1 c_1 r_2 c_2 \vdots r_K c_K
Output
If Takahashi can move from cell (1,1) to cell (H,W) by repeating the operation described in the problem, print Yes; otherwise, print No.
Sample Input 1
4 5 5 1 4 2 3 3 2 3 4 4 2
Sample Output 1
No
The grid looks as follows:

Takahashi cannot move from cell (1,1) to cell (4,5).
Sample Input 2
2 7 3 1 2 2 4 1 6
Sample Output 2
Yes
The grid looks as follows:

He can move from cell (1,1) to cell (2,7) by moving as shown in the figure.
Sample Input 3
1 1 0
Sample Output 3
Yes
Note that there may be cases where he does not need to move or where no obstacles are placed.
Sample Input 4
10 12 20 8 3 1 11 6 4 3 7 10 4 5 7 4 7 5 5 4 3 6 1 1 6 2 7 6 7 1 3 6 3 2 12 9 6 7 3 3 11 9 7
Sample Output 4
Yes