Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
高橋君は、ある web サイトに設定するパスワードを、英小文字のみからなる文字列 P にしようと考えています。
一方で、その web サイトのパスワードは長さ L 以上の文字列である必要があります。
P が長さの条件をみたすか、すなわち長さ L 以上の文字列であるか判定してください。
制約
- P は英小文字のみからなる長さ 1 以上 100 以下の文字列
- 1 \leq L \leq 100
- L は整数
入力
入力は以下の形式で標準入力から与えられる。
P L
出力
P が長さの条件をみたすならば Yes を、そうでないならば No を出力せよ。
入力例 1
chokudai 5
出力例 1
Yes
chokudai の長さは 8 であり、特に 5 以上であるため長さの条件をみたしています。
よって、Yes を出力します。
入力例 2
ac 3
出力例 2
No
ac の長さは 2 であり、特に 3 未満であるため長さの条件をみたしていません。
よって、No を出力します。
入力例 3
atcoder 7
出力例 3
Yes
atcoder の長さは 7 であり、特に 7 以上であるため長さの条件をみたしています。
よって、Yes を出力します。
Score : 100 points
Problem Statement
Takahashi wants to set his password for a certain website to a string P consisting of lowercase English letters.
The password for that website must be a string of length at least L.
Determine whether P satisfies the length condition, that is, whether it is a string of length at least L.
Constraints
- P is a string consisting of lowercase English letters with length between 1 and 100, inclusive.
- 1 \leq L \leq 100
- L is an integer.
Input
The input is given from Standard Input in the following format:
P L
Output
If P satisfies the length condition, print Yes; otherwise, print No.
Sample Input 1
chokudai 5
Sample Output 1
Yes
The length of chokudai is 8, which is at least 5, so it satisfies the length condition.
Thus, print Yes.
Sample Input 2
ac 3
Sample Output 2
No
The length of ac is 2, which is less than 3, so it does not satisfy the length condition.
Thus, print No.
Sample Input 3
atcoder 7
Sample Output 3
Yes
The length of atcoder is 7, which is at least 7, so it satisfies the length condition.
Thus, print Yes.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
N 個の駅、駅 1, 駅 2, \ldots, 駅 N が直線上にこの順に並んでいます。
ここで、1\leq i\leq N-1 について、駅 i と駅 (i+1) の間の距離は D_i です。
1\leq i<j\leq N をみたす整数の組 (i,j) それぞれについて、駅 i と駅 j の間の距離を求めてください。
なお、出力形式については出力の欄を参照してください。
制約
- 2 \leq N \leq 50
- 1 \leq D_i \leq 100
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N
D_1 D_2 \ldots D_{N-1}
出力
N-1 行出力せよ。
i 行目 (1\leq i\leq N-1) には、(N-i) 個の整数を空白区切りで出力せよ。
i 行目の j 番目 (1\leq j\leq N-i) には、駅 i と駅 (i+j) の間の距離を出力せよ。
入力例 1
5 5 10 2 3
出力例 1
5 15 17 20 10 12 15 2 5 3
各駅の間の距離は次のようになります。
- 駅 1 と駅 2 の間の距離は 5 です。
- 駅 1 と駅 3 の間の距離は 5+10=15 です。
- 駅 1 と駅 4 の間の距離は 5+10+2=17 です。
- 駅 1 と駅 5 の間の距離は 5+10+2+3=20 です。
- 駅 2 と駅 3 の間の距離は 10 です。
- 駅 2 と駅 4 の間の距離は 10+2=12 です。
- 駅 2 と駅 5 の間の距離は 10+2+3=15 です。
- 駅 3 と駅 4 の間の距離は 2 です。
- 駅 3 と駅 5 の間の距離は 2+3=5 です。
- 駅 4 と駅 5 の間の距離は 3 です。
よって、上記のように出力します。
入力例 2
2 100
出力例 2
100
Score : 200 points
Problem Statement
There are N stations, station 1, station 2, \ldots, station N, arranged in this order on a straight line.
Here, for 1\leq i\leq N-1, the distance between stations i and (i+1) is D_i.
For each pair of integers (i,j) satisfying 1\leq i<j\leq N, find the distance between stations i and j.
For the output format, refer to the Output section.
Constraints
- 2 \leq N \leq 50
- 1 \leq D_i \leq 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
D_1 D_2 \ldots D_{N-1}
Output
Output N-1 lines.
On the i-th line (1\leq i\leq N-1), output (N-i) integers, separated by spaces.
The j-th integer on the i-th line (1\leq j\leq N-i) should be the distance between stations i and (i+j).
Sample Input 1
5 5 10 2 3
Sample Output 1
5 15 17 20 10 12 15 2 5 3
The distances between stations are as follows:
- The distance between stations 1 and 2 is 5.
- The distance between stations 1 and 3 is 5+10=15.
- The distance between stations 1 and 4 is 5+10+2=17.
- The distance between stations 1 and 5 is 5+10+2+3=20.
- The distance between stations 2 and 3 is 10.
- The distance between stations 2 and 4 is 10+2=12.
- The distance between stations 2 and 5 is 10+2+3=15.
- The distance between stations 3 and 4 is 2.
- The distance between stations 3 and 5 is 2+3=5.
- The distance between stations 4 and 5 is 3.
Thus, output as shown above.
Sample Input 2
2 100
Sample Output 2
100
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
左右一列に N 個のマスが並んでいます。 最初、すべてのマスは白く塗られています。
Q 個のクエリを順に処理してください。i 個目のクエリでは 1 以上 N 以下の整数 A_i が与えられ、次の操作を行います。
左から A_i 番目のマスの色を反転させる。 具体的には、左から A_i 番目のマスが、白く塗られていたならば黒く塗り、黒く塗られていたならば白く塗る。
その後、黒く塗られたマスが連続している区間の個数を求める。ここで、黒く塗られたマスが連続している区間とは次をすべてみたす整数の組 (l,r) (1\leq l\leq r\leq N) を指す。
- 左から l, l+1, \ldots, r 番目のマスはすべて黒く塗られている。
- l=1 であるか、または左から (l-1) 番目のマスは白く塗られている。
- r=N であるか、または左から (r+1) 番目のマスは白く塗られている。
制約
- 1\leq N,Q\leq 5\times 10^5
- 1\leq A_i\leq N
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N Q A_1 A_2 \ldots A_Q
出力
Q 行出力せよ。i 行目 (1\leq i\leq Q) には i 個目のクエリの答えを出力せよ。
入力例 1
5 7 2 3 3 5 1 5 2
出力例 1
1 1 1 2 2 1 1
以下では、左から i 番目のマスを マス i と表します。
各クエリの後は次のような状態になっています。
- 1 個目のクエリの後、マス 2 のみが黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(2,2) の 1 つです。
- 2 個目のクエリの後、マス 2,3 が黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(2,3) の 1 つです。
- 3 個目のクエリの後、マス 2 のみが黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(2,2) の 1 つです。
- 4 個目のクエリの後、マス 2,5 が黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(2,2), (5,5) の 2 つです。
- 5 個目のクエリの後、マス 1,2,5 が黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(1,2), (5,5) の 2 つです。
- 6 個目のクエリの後、マス 1,2 のみが黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(1,2) の 1 つです。
- 7 個目のクエリの後、マス 1 のみが黒く塗られています。黒く塗られたマスが連続している区間は (l,r)=(1,1) の 1 つです。
よって、1,1,1,2,2,1,1 を改行区切りで出力します。
入力例 2
1 2 1 1
出力例 2
1 0
2 個目のクエリの後、すべてのマスは白く塗られているため、2 行目には 0 を出力します。
入力例 3
3 3 1 3 2
出力例 3
1 2 1
Score : 350 points
Problem Statement
There are N squares arranged in a row from left to right. Initially, all squares are painted white.
Process Q queries in order. The i-th query gives an integer A_i between 1 and N, inclusive, and performs the following operation:
Flip the color of the A_i-th square from the left. Specifically, if the A_i-th square from the left is painted white, paint it black; if it is painted black, paint it white.
Then, find the number of intervals of consecutively painted black squares.Here, an interval of consecutively painted black squares is a pair of integers (l,r) (1\leq l\leq r\leq N) that satisfy all of the following:
- The l-th, (l+1)-th, \ldots, r-th squares from the left are all painted black.
- Either l=1, or the (l-1)-th square from the left is painted white.
- Either r=N, or the (r+1)-th square from the left is painted white.
Constraints
- 1\leq N,Q\leq 5\times 10^5
- 1\leq A_i\leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q A_1 A_2 \ldots A_Q
Output
Output Q lines. On the i-th line (1\leq i\leq Q), output the answer to the i-th query.
Sample Input 1
5 7 2 3 3 5 1 5 2
Sample Output 1
1 1 1 2 2 1 1
Below, the i-th square from the left is referred to as square i.
After each query, the state is as follows:
- After the 1st query, only square 2 is painted black. There is 1 interval of consecutively painted black squares: (l,r)=(2,2).
- After the 2nd query, squares 2,3 are painted black. There is 1 interval of consecutively painted black squares: (l,r)=(2,3).
- After the 3rd query, only square 2 is painted black. There is 1 interval of consecutively painted black squares: (l,r)=(2,2).
- After the 4th query, squares 2,5 are painted black. There are 2 intervals of consecutively painted black squares: (l,r)=(2,2), (5,5).
- After the 5th query, squares 1,2,5 are painted black. There are 2 intervals of consecutively painted black squares: (l,r)=(1,2), (5,5).
- After the 6th query, only squares 1,2 are painted black. There is 1 interval of consecutively painted black squares: (l,r)=(1,2).
- After the 7th query, only square 1 is painted black. There is 1 interval of consecutively painted black squares: (l,r)=(1,1).
Thus, output 1,1,1,2,2,1,1 separated by newlines.
Sample Input 2
1 2 1 1
Sample Output 2
1 0
After the 2nd query, all squares are painted white, so output 0 on the 2nd line.
Sample Input 3
3 3 1 3 2
Sample Output 3
1 2 1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
1 台のサーバーと N 台の PC があります。 サーバーおよび各 PC はそれぞれ 1 つずつ文字列を保持しており、最初は全て空文字列です。
Q 個のクエリが与えられます。各クエリは以下のいずれかの形式です。
1 p:PC p の文字列をサーバーの文字列で置き換える。2 p s:PC p の文字列の末尾に文字列 s を追加する。3 p:サーバーの文字列をPC p の文字列で置き換える。
全てのクエリを与えられた順に処理したときの最終的なサーバーの文字列を求めてください。
制約
- N,Q は整数
- 1\leq N,Q \leq 2\times 10^5
- 全てのクエリについて、p は整数であり、1 \leq p\leq N
- 全ての 2 種類目のクエリについて、s は英小文字からなる長さ 1 以上の文字列
- 全ての 2 種類目のクエリに対する s の長さの総和は 10^6 以下
入力
入力は以下の形式で標準入力から与えられる。
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
ここで \mathrm{query}_i は i 番目のクエリを表し、以下のいずれかの形式で与えられる。
1 p
2 p s
3 p
出力
答えを出力せよ。
入力例 1
2 6 2 1 at 3 1 2 2 on 1 2 2 2 coder 3 2
出力例 1
atcoder
- 最初、サーバーおよび PC 1,2 の文字列は全て空である。
- 1 番目のクエリ: PC 1 の文字列の末尾に
atを追加する。このとき、サーバー、PC 1,2 の文字列はそれぞれ空、at、空である。 - 2 番目のクエリ: サーバーの文字列を PC 1 の文字列で置き換える。このとき、サーバー、PC 1,2 の文字列はそれぞれ
at、at、空である。 - 3 番目のクエリ: PC 2 の文字列の末尾に
onを追加する。このとき、サーバー、PC 1,2 の文字列はそれぞれat、at、onである。 - 4 番目のクエリ: PC 2 の文字列をサーバーの文字列で置き換える。このとき、サーバー、PC 1,2 の文字列はそれぞれ
at、at、atである。 - 5 番目のクエリ: PC 2 の文字列の末尾に
coderを追加する。このとき、サーバー、PC 1,2 の文字列はそれぞれat、at、atcoderである。 - 6 番目のクエリ: サーバーの文字列を PC 2 の文字列で置き換える。このとき、サーバー、PC 1,2 の文字列はそれぞれ
atcoder、at、atcoderである。
よって、最終的なサーバーの文字列は atcoder です。
入力例 2
100000 3 1 100 2 300 abc 3 200
出力例 2
最終的なサーバーの文字列は空です。
入力例 3
10 10 2 7 ladxf 2 7 zz 2 7 kfm 3 7 1 5 2 5 irur 3 5 1 6 2 6 ptilun 3 6
出力例 3
ladxfzzkfmirurptilun
Score : 425 points
Problem Statement
There is one server and N PCs. The server and each PC each hold one string, and initially all strings are empty.
Q queries are given. Each query is in one of the following formats:
1 p: Replace the string of PC p with the string of the server.2 p s: Append string s to the end of the string of PC p.3 p: Replace the string of the server with the string of PC p.
Find the final string of the server after processing all queries in the given order.
Constraints
- N,Q are integers
- 1\leq N,Q \leq 2\times 10^5
- For every query, p is an integer and 1 \leq p\leq N.
- For every query of type 2, s is a string of length at least 1 consisting of lowercase English letters.
- The sum of the lengths of s over all queries of type 2 is at most 10^6.
Input
The input is given from Standard Input in the following format:
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
Here, \mathrm{query}_i represents the i-th query and is given in one of the following formats:
1 p
2 p s
3 p
Output
Output the answer.
Sample Input 1
2 6 2 1 at 3 1 2 2 on 1 2 2 2 coder 3 2
Sample Output 1
atcoder
- Initially, the strings of the server and PCs 1,2 are all empty.
- 1st query: Append
atto the end of the string of PC 1. At this time, the strings of the server, PC 1,2 are empty,at, empty, respectively. - 2nd query: Replace the string of the server with the string of PC 1. At this time, the strings of the server, PC 1,2 are
at,at, empty, respectively. - 3rd query: Append
onto the end of the string of PC 2. At this time, the strings of the server, PC 1,2 areat,at,on, respectively. - 4th query: Replace the string of PC 2 with the string of the server. At this time, the strings of the server, PC 1,2 are
at,at,at, respectively. - 5th query: Append
coderto the end of the string of PC 2. At this time, the strings of the server, PC 1,2 areat,at,atcoder, respectively. - 6th query: Replace the string of the server with the string of PC 2. At this time, the strings of the server, PC 1,2 are
atcoder,at,atcoder, respectively.
Thus, the final string of the server is atcoder.
Sample Input 2
100000 3 1 100 2 300 abc 3 200
Sample Output 2
The final string of the server is empty.
Sample Input 3
10 10 2 7 ladxf 2 7 zz 2 7 kfm 3 7 1 5 2 5 irur 3 5 1 6 2 6 ptilun 3 6
Sample Output 3
ladxfzzkfmirurptilun
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 450 点
問題文
N 個の六面サイコロがあります。 サイコロには 1 から N までの番号が付けられており、サイコロ i の各面に書かれた数はそれぞれ A_{i,1},A_{i,2},\dots,A_{i,6} です。
今からこれら N 個のサイコロを全て同時に振ります。 各サイコロの上を向いた面に書かれた数の最大値の期待値を \bmod\ 998244353 で求めてください。
なお、いずれのサイコロについても、そのサイコロを振った際に上を向く面は独立かつ一様ランダムに選ばれるものとします。
期待値を \bmod\ 998244353 で求めるとは
求める期待値は必ず有理数になることが証明できます。 また、この問題の制約のもとでは、その値を既約分数 \frac{P}{Q} で表した時、Q \not\equiv 0 \pmod{998244353} となることも証明できます。 よって、R \times Q \equiv P \pmod{998244353}, 0 \leq R < 998244353 を満たす整数 R が一意に定まります。 この R を求めてください。
制約
- 1\leq N \leq 10^5
- 1\leq A_{i,j} \leq 10^9
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
A_{1,1} A_{1,2} \dots A_{1,6}
A_{2,1} A_{2,2} \dots A_{2,6}
\vdots
A_{N,1} A_{N,2} \dots A_{N,6}
出力
答えを出力せよ。
入力例 1
2 1 1 4 4 4 4 1 1 1 3 3 3
出力例 1
332748121
サイコロ i の上を向いた面に書かれた数を x_i とします。
- x_1=1,x_2=1 のケース:\frac{2}{6}\times\frac{3}{6}=\frac{1}{6} の確率で発生し、上を向いた面に書かれた数の最大値は 1 です。
- x_1=1,x_2=3 のケース:\frac{2}{6}\times\frac{3}{6}=\frac{1}{6} の確率で発生し、上を向いた面に書かれた数の最大値は 3 です。
- x_1=4,x_2=1 のケース:\frac{4}{6}\times\frac{3}{6}=\frac{1}{3} の確率で発生し、上を向いた面に書かれた数の最大値は 4 です。
- x_1=4,x_2=3 のケース:\frac{4}{6}\times\frac{3}{6}=\frac{1}{3} の確率で発生し、上を向いた面に書かれた数の最大値は 4 です。
よって、求める期待値は \frac{1}{6}\times 1 + \frac{1}{6}\times 3 + \frac{1}{3}\times 4 + \frac{1}{3}\times 4 = \frac{10}{3} \equiv 332748121 \pmod{998244353} です。
入力例 2
2 1 1 1 1 1 1 2 2 2 2 2 2
出力例 2
2
サイコロ 1,2 の上を向いた面に書かれた数はそれぞれ常に 1,2 であり、その最大値は常に 2 です。
入力例 3
8 55 76 80 21 34 28 82 84 2 32 56 17 11 57 37 28 39 18 47 2 97 25 75 29 72 45 22 75 26 81 6 79 16 68 68 40 31 80 68 57 18 55 49 10 63 91 93 40
出力例 3
213725517
Score : 450 points
Problem Statement
There are N six-sided dice. The dice are numbered from 1 to N, and the numbers written on the faces of die i are A_{i,1},A_{i,2},\dots,A_{i,6}.
Now, all N dice will be rolled simultaneously. Find the expected value, modulo 998244353, of the maximum value among the numbers written on the face that comes up on each die.
For any die, the face that comes up when the die is rolled is chosen independently and uniformly at random.
Finding the expected value modulo 998244353
It can be proved that the expected value to be found is always a rational number. Also, under the constraints of this problem, it can be proved that when the value is expressed as an irreducible fraction \frac{P}{Q}, we have Q \not\equiv 0 \pmod{998244353}. Therefore, there exists a unique integer R such that R \times Q \equiv P \pmod{998244353}, 0 \leq R < 998244353. Find this R.
Constraints
- 1\leq N \leq 10^5
- 1\leq A_{i,j} \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
A_{1,1} A_{1,2} \dots A_{1,6}
A_{2,1} A_{2,2} \dots A_{2,6}
\vdots
A_{N,1} A_{N,2} \dots A_{N,6}
Output
Output the answer.
Sample Input 1
2 1 1 4 4 4 4 1 1 1 3 3 3
Sample Output 1
332748121
Let x_i be the number written on the face that comes up on die i.
- Case x_1=1,x_2=1: Occurs with probability \frac{2}{6}\times\frac{3}{6}=\frac{1}{6}, and the maximum value among the numbers written on the faces that come up is 1.
- Case x_1=1,x_2=3: Occurs with probability \frac{2}{6}\times\frac{3}{6}=\frac{1}{6}, and the maximum value among the numbers written on the faces that come up is 3.
- Case x_1=4,x_2=1: Occurs with probability \frac{4}{6}\times\frac{3}{6}=\frac{1}{3}, and the maximum value among the numbers written on the faces that come up is 4.
- Case x_1=4,x_2=3: Occurs with probability \frac{4}{6}\times\frac{3}{6}=\frac{1}{3}, and the maximum value among the numbers written on the faces that come up is 4.
Thus, the expected value to be found is \frac{1}{6}\times 1 + \frac{1}{6}\times 3 + \frac{1}{3}\times 4 + \frac{1}{3}\times 4 = \frac{10}{3} \equiv 332748121 \pmod{998244353}.
Sample Input 2
2 1 1 1 1 1 1 2 2 2 2 2 2
Sample Output 2
2
The numbers written on the faces that come up on dice 1,2 are always 1,2, respectively, and their maximum value is always 2.
Sample Input 3
8 55 76 80 21 34 28 82 84 2 32 56 17 11 57 37 28 39 18 47 2 97 25 75 29 72 45 22 75 26 81 6 79 16 68 68 40 31 80 68 57 18 55 49 10 63 91 93 40
Sample Output 3
213725517
Time Limit: 4 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
N 頂点 M 辺の無向グラフ G_0 が与えられます。 G_0 の頂点および辺は、それぞれ頂点 1, 頂点 2, \ldots, 頂点 N および辺 1, 辺 2, \ldots, 辺 M と番号づけられており、 辺 i (1\leq i\leq M) は頂点 U_i と頂点 V_i を結んでいます。
高橋君はグラフ G と、駒 1, 駒 2, \ldots, 駒 N と番号づけられた N 個の駒を持っています。
最初、G=G_0 であり、さらに G の頂点 i (1\leq i\leq N) には駒 i が置かれています。
高橋君はこれから Q 回の操作を順に行います。 i 回目 (1\leq i\leq Q) の操作では 1 以上 M 以下の整数 X_i が与えられ、次の操作を行います。
G において駒 U_{X_i} と駒 V_{X_i} が異なる頂点に置かれており、 それらの間に( G 上の)辺 e が存在するならばその辺を縮約したグラフ G' を作成する。 この際、自己ループができた場合は取り除き、多重辺が存在した場合は単純辺に置き換える。
その後、G において辺 e が結んでいた 2 頂点に置かれていた駒はすべて、G' の e の縮約によって新たに生成された頂点に置く。 G 上のその他の頂点に置かれていた駒については、G' の対応する頂点に置く。 最後に、このようにしてできた G' を新たな G とする。
駒 U_{X_i} と駒 V_{X_i} が同じ頂点に置かれていた場合、あるいは置かれている頂点の間が辺で結ばれていなかった場合は何も行わない。
i=1,2,\ldots, Q 回目の操作それぞれについて、i 回目の操作の後の G の辺の数を出力してください。
辺の縮約 とは
頂点 u と頂点 v を結ぶ辺の縮約とは、頂点 u,v を 1 つの頂点にまとめる操作です。 より正確には、G に対して辺の縮約を行なって得られるグラフとは G に対して次の操作を行って得られるものを指します。- G に新たに頂点 w を追加する。
- G 上の u,v 以外の各頂点 x について、u と x を結ぶ辺、あるいは v と x を結ぶ辺の少なくとも一方が存在するとき、かつその時に限り、w と x を結ぶ辺を加える。
- 頂点 u,v を削除し、頂点 u と v を結ぶ辺および頂点 u または v と他の頂点を結ぶ辺をすべて削除する。
制約
- 2\leq N\leq 3\times 10^5
- 1\leq M\leq 3\times 10^5
- 1\leq U_i<V_i\leq N
- i\neq j ならば (U_i,V_i)\neq (U_j,V_j)
- 1\leq Q\leq 3\times 10^5
- 1\leq X_i\leq M
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 U_2 V_2 \vdots U_M V_M Q X_1 X_2 \ldots X_Q
出力
Q 行出力せよ。 i 行目 (1\leq i\leq Q) には、i 回目の操作の後の G の辺の数を出力せよ。
入力例 1
7 7 1 2 1 3 2 3 1 4 1 5 2 5 6 7 5 1 2 3 1 5
出力例 1
4 3 3 3 2
最初、G は下図のようになっています。丸付き数字はその番号の駒を表します。
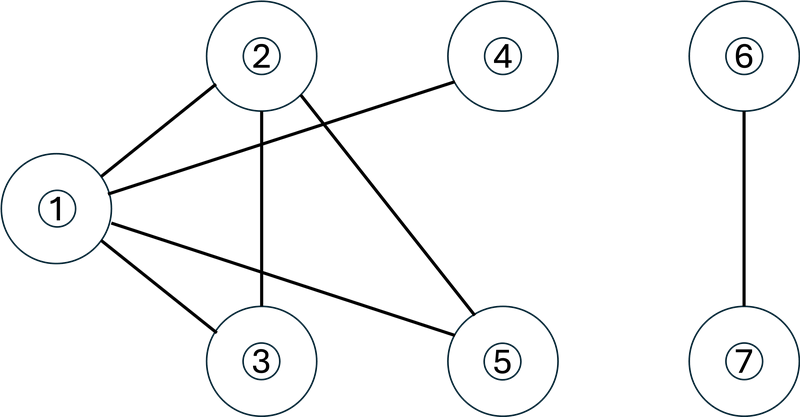
1 回目の操作では、駒 1 と駒 2 が置かれている頂点の間の辺(下図左)の縮約を行います。
操作後、G は下図右のようになり、特に辺の数は 4 です。
自己ループの削除および多重辺の単純辺への置換が行われていることに注意してください。
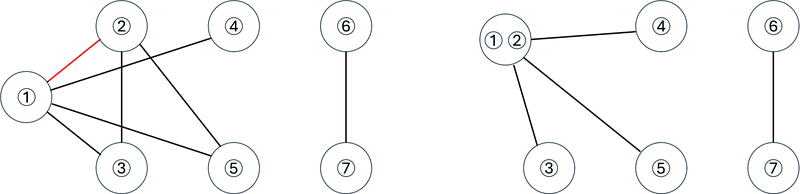
2 回目の操作では、駒 1 と駒 3 が置かれている頂点の間の辺の縮約を行います。
操作後、G は下図左のようになり、辺の数は 3 となります。
3 回目の操作では、駒 2 と駒 3 は同じ頂点に置かれているため、G はそのままであり、辺の数も 3 のままです。
4 回目の操作でも、駒 1 と駒 2 は同じ頂点に置かれているため、G はそのままであり、辺の数も 3 のままです。
5 回目の操作では、駒 1 と駒 5 が置かれている頂点の間の辺の縮約を行います。
操作後、G は下図右のようになり、辺の数は 2 となります。
よって、4,3,3,3,2 をこの順に改行区切りで出力します。
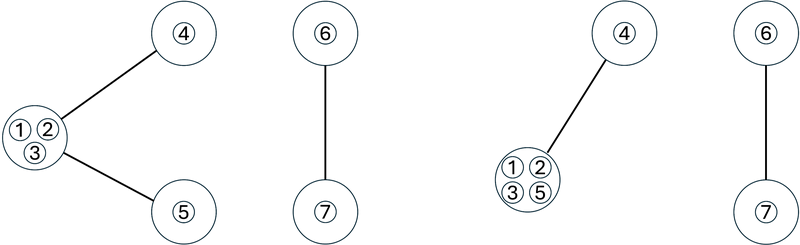
Score : 525 points
Problem Statement
You are given an undirected graph G_0 with N vertices and M edges. The vertices and edges of G_0 are numbered as vertices 1, 2, \ldots, N and edges 1, 2, \ldots, M, respectively, and edge i (1\leq i\leq M) connects vertices U_i and V_i.
Takahashi has a graph G and N pieces numbered as pieces 1, 2, \ldots, N.
Initially, G=G_0, and piece i (1\leq i\leq N) is placed on vertex i of G.
He will now perform Q operations in order. The i-th operation (1\leq i\leq Q) gives an integer X_i between 1 and M, inclusive, and performs the following operation:
In G, if pieces U_{X_i} and V_{X_i} are placed on different vertices and there exists an edge e (on G) between them, create a graph G' by contracting that edge. In this case, if self-loops are created, remove them, and if multi-edges exist, replace them with simple edges.
Then, all pieces that were placed on the two vertices connected by edge e in G are placed on the newly generated vertex by the contraction of e in G'. Pieces that were placed on other vertices in G are placed on the corresponding vertices in G'. Finally, set this resulting G' as the new G.
If pieces U_{X_i} and V_{X_i} are placed on the same vertex, or if the vertices they are placed on are not connected by an edge, do nothing.
For each of the operations i=1,2,\ldots, Q, output the number of edges in G after the i-th operation.
Edge Contraction
Edge contraction of an edge connecting vertices u and v is an operation that merges vertices u,v into one vertex. More precisely, a graph obtained by performing edge contraction on G refers to the result of performing the following operations on G:- Add a new vertex w to G.
- For each vertex x other than u,v in G, if and only if at least one of the edge connecting u and x or the edge connecting v and x exists, add an edge connecting w and x.
- Delete vertices u,v and remove all edges connecting vertices u and v, as well as all edges connecting vertex u or vertex v with other vertices.
Constraints
- 2\leq N\leq 3\times 10^5
- 1\leq M\leq 3\times 10^5
- 1\leq U_i<V_i\leq N
- (U_i,V_i)\neq (U_j,V_j) if i\neq j.
- 1\leq Q\leq 3\times 10^5
- 1\leq X_i\leq M
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M U_1 V_1 U_2 V_2 \vdots U_M V_M Q X_1 X_2 \ldots X_Q
Output
Output Q lines. On the i-th line (1\leq i\leq Q), output the number of edges in G after the i-th operation.
Sample Input 1
7 7 1 2 1 3 2 3 1 4 1 5 2 5 6 7 5 1 2 3 1 5
Sample Output 1
4 3 3 3 2
Initially, G is as shown in the figure below. The circled numbers represent pieces with those numbers.

In the 1st operation, we contract the edge between the vertices where pieces 1 and 2 are placed (left figure below).
After the operation, G becomes as shown in the right figure below, and in particular, the number of edges is 4.
Note that self-loops have been removed and multi-edges have been replaced with simple edges.

In the 2nd operation, we contract the edge between the vertices where pieces 1 and 3 are placed.
After the operation, G becomes as shown in the left figure below, and the number of edges becomes 3.
In the 3rd operation, since pieces 2 and 3 are placed on the same vertex, G remains unchanged, and the number of edges remains 3.
In the 4th operation as well, since pieces 1 and 2 are placed on the same vertex, G remains unchanged, and the number of edges remains 3.
In the 5th operation, we contract the edge between the vertices where pieces 1 and 5 are placed.
After the operation, G becomes as shown in the right figure below, and the number of edges becomes 2.
Thus, output 4,3,3,3,2 in this order, separated by newlines.

Time Limit: 6 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
N 頂点 M 辺の無向グラフ G があります。 G は自己ループを含みませんが、多重辺は含む可能性があります。 頂点には 1 から N までの、辺には 1 から M までの番号がそれぞれ付けられており、辺 i は頂点 U_i,V_i の間に張られています。
G に含まれるサイクルの個数を 998244353 で割った余りを求めてください。
より形式的には、与えられた辺集合の部分集合 \lbrace e_1,e_2,\dots,e_k\rbrace \subseteq \lbrace 1,2,\dots,M\rbrace\ (k\geq 2) であって以下の条件を満たすものの個数を 998244353 で割った余りを求めてください。
- (e_1,e_2,\dots,e_k) の並び替え (e_1',e_2',\dots,e_k') および頂点列 (v_1,v_2,\dots,v_k) の組であって、以下を全て満たすものが存在する。
- v_1,v_2,\dots,v_k は互いに相異なる
- 全ての j\ (1\leq j\leq k) について、辺 e_j' は頂点 v_j,v_{(j\bmod k) + 1} の間に張られている
制約
- 2\leq N \leq 20
- 2\leq M \leq 2\times 10^5
- 1\leq U_i < V_i \leq N
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 U_2 V_2 \vdots U_M V_M
出力
答えを出力せよ。
入力例 1
3 4 1 3 1 2 2 3 1 3
出力例 1
3
以下の図の通り、全部で 3 個のサイクルが存在します。 丸の中に書かれた数字と線の横に書かれた数字はそれぞれ頂点番号、辺番号を表します。 赤い線がサイクルに含まれる辺、黒い線がそれ以外の辺を表します。
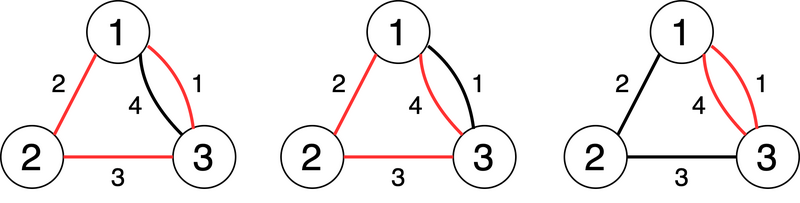
左から順に、辺集合 \lbrace 1,2,3 \rbrace,\lbrace 2,3,4 \rbrace,\lbrace 1,4 \rbrace をそれぞれ選ぶことに対応しています。
入力例 2
4 2 1 4 2 3
出力例 2
0
入力例 3
5 15 1 5 3 4 2 3 2 4 3 5 4 5 2 5 2 3 1 3 4 5 2 5 4 5 1 2 3 4 1 5
出力例 3
166
Score : 600 points
Problem Statement
There is an undirected graph G with N vertices and M edges. G does not contain self-loops, but may contain multi-edges. Vertices are numbered from 1 to N, and edges are numbered from 1 to M, with edge i connecting vertices U_i,V_i.
Find the number, modulo 998244353, of cycles contained in G.
More formally, find the number, modulo 998244353, of subsets \lbrace e_1,e_2,\dots,e_k\rbrace \subseteq \lbrace 1,2,\dots,M\rbrace\ (k\geq 2) of the given edge set that satisfy the following condition.
- There exists a permutation (e_1',e_2',\dots,e_k') of (e_1,e_2,\dots,e_k) and a vertex sequence (v_1,v_2,\dots,v_k) such that all of the following hold:
- v_1,v_2,\dots,v_k are pairwise distinct;
- For all j\ (1\leq j\leq k), edge e_j' connects vertices v_j,v_{(j\bmod k) + 1}.
Constraints
- 2\leq N \leq 20
- 2\leq M \leq 2\times 10^5
- 1\leq U_i < V_i \leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M U_1 V_1 U_2 V_2 \vdots U_M V_M
Output
Output the answer.
Sample Input 1
3 4 1 3 1 2 2 3 1 3
Sample Output 1
3
As shown in the figure below, there are a total of 3 cycles. The numbers inside the circles and the numbers next to the lines represent vertex numbers and edge numbers, respectively. Red lines represent edges included in cycles, and black lines represent the other edges.

From left to right, these correspond to choosing edge sets \lbrace 1,2,3 \rbrace,\lbrace 2,3,4 \rbrace,\lbrace 1,4 \rbrace, respectively.
Sample Input 2
4 2 1 4 2 3
Sample Output 2
0
Sample Input 3
5 15 1 5 3 4 2 3 2 4 3 5 4 5 2 5 2 3 1 3 4 5 2 5 4 5 1 2 3 4 1 5
Sample Output 3
166