Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
AtCoder 国では馬のレースが N 個開催されています。
i 個目のレースには A_i 歳以下の馬が出場できます。
N 個のレースのうち、 K 歳の馬が出場できるレースの個数はいくつですか?
制約
- 入力は全て整数
- 1 \le N \le 100
- 1 \le A_i \le 100
- 1 \le K \le 100
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \dots A_N K
出力
答えを整数として出力せよ。
入力例 1
5 3 1 4 1 5 4
出力例 1
2
- 1 個目のレースには 3 歳以下の馬が出場できます。
- 2 個目のレースには 1 歳以下の馬が出場できます。
- 3 個目のレースには 4 歳以下の馬が出場できます。
- 4 個目のレースには 1 歳以下の馬が出場できます。
- 5 個目のレースには 5 歳以下の馬が出場できます。
5 個のレースのうち、 4 歳の馬が出場できるものは 3,5 個目の 2 つです。
入力例 2
1 1 100
出力例 2
0
K 歳の馬が出場できるレースがひとつもない場合もあります。
入力例 3
15 18 89 31 2 15 93 64 78 58 19 79 59 24 50 30 38
出力例 3
8
Score : 100 points
Problem Statement
In AtCoder Kingdom, there are N horse races being held.
Horses aged A_i or younger can participate in the i-th race.
Among the N races, how many races can a K-year-old horse participate in?
Constraints
- All input values are integers.
- 1 \le N \le 100
- 1 \le A_i \le 100
- 1 \le K \le 100
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \dots A_N K
Output
Output the answer as an integer.
Sample Input 1
5 3 1 4 1 5 4
Sample Output 1
2
- Horses aged 3 or younger can participate in the 1st race.
- Horses aged 1 or younger can participate in the 2nd race.
- Horses aged 4 or younger can participate in the 3rd race.
- Horses aged 1 or younger can participate in the 4th race.
- Horses aged 5 or younger can participate in the 5th race.
Among the 5 races, a 4-year-old horse can participate in the 3rd and 5th races, which is 2 races.
Sample Input 2
1 1 100
Sample Output 2
0
There may be no races that a K-year-old horse can participate in.
Sample Input 3
15 18 89 31 2 15 93 64 78 58 19 79 59 24 50 30 38
Sample Output 3
8
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
1,2,\dots,N の番号が付いた N 個の箱があります。最初は全ての箱が空です。
これから Q 個のボールが順番にやってきます。
高橋君は、数列 X=(X_1,X_2,\dots,X_Q) に従ってボールを箱に入れます。
具体的には、 i 番目にやってきたボールに次の処理を行います。
- X_i \ge 1 である場合 : このボールを、箱 X_i に入れる。
- X_i = 0 である場合 : このボールを、現在入っているボールが最も少ない箱のうち番号が最小である箱に入れる。
それぞれのボールをどの箱に入れたかを求めてください。
制約
- 入力は全て整数
- 1 \le N \le 100
- 1 \le Q \le 100
- 0 \le X_i \le N
入力
入力は以下の形式で標準入力から与えられる。
N Q X_1 X_2 \dots X_Q
出力
i 番目にやってきたボールを箱 B_i に入れたとき、次の形式に従って出力せよ。
B_1 B_2 \dots B_Q
入力例 1
4 5 2 0 3 0 0
出力例 1
2 1 3 4 1
箱が 4 つあり、ボールは 5 個やってきます。
- 最初、全ての箱は空です。
- 各箱に入っているボールの数は箱 1 から順に 0,0,0,0 個です。
- X_1=2 なので、 1 番目にやってきたボールを箱 2 に入れます。
- 各箱に入っているボールの数は箱 1 から順に 0,1,0,0 個となります。
- X_2=0 なので、 2 番目にやってきたボールを現在入っているボールが最も少ない箱のうち番号が最小である箱である箱 1 に入れます。
- 各箱に入っているボールの数は箱 1 から順に 1,1,0,0 個となります。
- X_3=3 なので、 3 番目にやってきたボールを箱 3 に入れます。
- 各箱に入っているボールの数は箱 1 から順に 1,1,1,0 個となります。
- X_4=0 なので、 4 番目にやってきたボールを現在入っているボールが最も少ない箱のうち番号が最小である箱である箱 4 に入れます。
- 各箱に入っているボールの数は箱 1 から順に 1,1,1,1 個となります。
- X_5=0 なので、 5 番目にやってきたボールを現在入っているボールが最も少ない箱のうち番号が最小である箱である箱 1 に入れます。
- 各箱に入っているボールの数は箱 1 から順に 2,1,1,1 個となります。
各ボールを、やってきた順に箱 2,1,3,4,1 に入れました。よって、 2 1 3 4 1 と出力します。
入力例 2
3 7 1 1 0 0 0 0 0
出力例 2
1 1 2 3 2 3 1
入力例 3
6 20 4 6 0 3 4 2 6 5 2 3 0 3 2 5 0 3 5 0 2 0
出力例 3
4 6 1 3 4 2 6 5 2 3 1 3 2 5 1 3 5 4 2 6
Score : 200 points
Problem Statement
There are N boxes numbered 1,2,\dots,N. Initially, all boxes are empty.
Q balls will come in order.
Takahashi will put the balls into the boxes according to the sequence X=(X_1,X_2,\dots,X_Q).
Specifically, he performs the following process for the i-th ball:
- If X_i \ge 1: Put this ball into box X_i.
- If X_i = 0: Put this ball into the box with the smallest number among those containing the fewest balls.
Find which box each ball was put into.
Constraints
- All input values are integers.
- 1 \le N \le 100
- 1 \le Q \le 100
- 0 \le X_i \le N
Input
The input is given from Standard Input in the following format:
N Q X_1 X_2 \dots X_Q
Output
If the i-th ball was put into box B_i, output in the following format:
B_1 B_2 \dots B_Q
Sample Input 1
4 5 2 0 3 0 0
Sample Output 1
2 1 3 4 1
There are 4 boxes, and 5 balls come.
- Initially, all boxes are empty.
- The numbers of balls in box 1,2,3,4 are 0,0,0,0, respectively.
- Since X_1=2, put the 1st ball into box 2.
- The numbers of balls in box 1,2,3,4 are 0,1,0,0, respectively.
- Since X_2=0, put the 2nd ball into box 1, which has the smallest number among those containing the fewest balls.
- The numbers of balls in box 1,2,3,4 are 1,1,0,0, respectively.
- Since X_3=3, put the 3rd ball into box 3.
- The numbers of balls in box 1,2,3,4 are 1,1,1,0, respectively.
- Since X_4=0, put the 4th ball into box 4, which has the smallest number among those containing the fewest balls.
- The numbers of balls in box 1,2,3,4 are 1,1,1,1, respectively.
- Since X_5=0, put the 5th ball into box 1, which has the smallest number among those containing the fewest balls.
- The numbers of balls in box 1,2,3,4 are 2,1,1,1, respectively.
The balls were put into boxes 2,1,3,4,1 in order. Thus, output 2 1 3 4 1.
Sample Input 2
3 7 1 1 0 0 0 0 0
Sample Output 2
1 1 2 3 2 3 1
Sample Input 3
6 20 4 6 0 3 4 2 6 5 2 3 0 3 2 5 0 3 5 0 2 0
Sample Output 3
4 6 1 3 4 2 6 5 2 3 1 3 2 5 1 3 5 4 2 6
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
長さ N の整数列 A があり、最初 A_i = i です。 以下のクエリを全部で Q 個処理してください。
- タイプ 1 : A_p を x に変更する。
- タイプ 2 : A_p を出力する。
- タイプ 3 : 「 A の先頭の要素を末尾にする」という操作を k 回繰り返す。
- 厳密には、 A を (A_2,A_3,\dots,A_N,A_1) に置き換えることを k 回繰り返す。
制約
- 入力は全て整数
- 1 \le N \le 10^6
- 1 \le Q \le 3 \times 10^5
- 全てのクエリは以下の制約を満たす
- 1 \le p \le N
- 1 \le x \le 10^6
- 1 \le k \le 10^9
入力
入力は以下の形式で標準入力から与えられる。
N Q
\rm{Query}_1
\rm{Query}_2
\vdots
\rm{Query}_Q
但し、 \rm{Query}_i は i 個目のクエリを表す。
タイプ 1 のクエリは以下の形式で与えられる。
1 p x
タイプ 2 のクエリは以下の形式で与えられる。
2 p
タイプ 3 のクエリは以下の形式で与えられる。
3 k
出力
タイプ 2 のクエリが現れる度に、その解答を 1 行に出力せよ。
入力例 1
5 5 2 3 1 2 1000000 3 4 2 2 2 3
出力例 1
3 1 1000000
この入力には 5 個のクエリが含まれます。
- 最初、 A=(1,2,3,4,5) です。
- 1 番目のクエリはタイプ 2 で、 A_3=3 を出力します。
- 2 番目のクエリはタイプ 1 で、 A_2=1000000 に置き換えます。
- クエリの結果、 A=(1,1000000,3,4,5) となります。
- 3 番目のクエリはタイプ 3 で、「 A の先頭の要素を末尾にする」という操作を 4 回繰り返します。
- クエリの結果、 A=(5,1,1000000,3,4) となります。
- 4 番目のクエリはタイプ 2 で、 A_2=1 を出力します。
- 5 番目のクエリはタイプ 2 で、 A_3=1000000 を出力します。
入力例 2
1000000 2 1 1000000 999999 3 1000000000
出力例 2
出力が空である場合もあります。
Score : 300 points
Problem Statement
There is an integer sequence A of length N, initially A_i = i. Process a total of Q queries of the following types:
- Type 1: Change A_p to x.
- Type 2: Output A_p.
- Type 3: Repeat the operation "move the first element of A to the end" k times.
- Formally, replace A with (A_2,A_3,\dots,A_N,A_1) k times.
Constraints
- All input values are integers.
- 1 \le N \le 10^6
- 1 \le Q \le 3 \times 10^5
- All queries satisfy the following constraints:
- 1 \le p \le N
- 1 \le x \le 10^6
- 1 \le k \le 10^9
Input
The input is given from Standard Input in the following format:
N Q
\rm{Query}_1
\rm{Query}_2
\vdots
\rm{Query}_Q
Here, \rm{Query}_i represents the i-th query.
Type 1 queries are given in the following format:
1 p x
Type 2 queries are given in the following format:
2 p
Type 3 queries are given in the following format:
3 k
Output
For each Type 2 query, output the answer on a line.
Sample Input 1
5 5 2 3 1 2 1000000 3 4 2 2 2 3
Sample Output 1
3 1 1000000
This input contains 5 queries.
- Initially, A=(1,2,3,4,5).
- The 1st query is Type 2: output A_3=3.
- The 2nd query is Type 1: replace A_2 with 1000000.
- After the query, A=(1,1000000,3,4,5).
- The 3rd query is Type 3: repeat the operation "move the first element of A to the end" 4 times.
- After the query, A=(5,1,1000000,3,4).
- The 4th query is Type 2: output A_2=1.
- The 5th query is Type 2: output A_3=1000000.
Sample Input 2
1000000 2 1 1000000 999999 3 1000000000
Sample Output 2
The output may be empty.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
頂点に 1 から N の、辺に 1 から M の番号がついたN 頂点 M 辺の有向グラフがあります。辺 i は頂点 A_i から頂点 B_i への重み W_i の有向辺です。
頂点 1 から頂点 N への walk のうち、walk に含まれる辺の重みのビット単位 \mathrm{XOR} の最小値を求めてください。
頂点 1 から頂点 N への walk とは
直感的には、「頂点 1 から頂点 N への経路であって、同じ頂点や同じ辺を複数回通っても良いもの」です。 正確には、辺の列 (e_1,\ldots,e_k) であって、以下の条件を全て満たすものです。
- e_1 は頂点 1 を始点とする。
- 全ての 1 \leq i < k について、e_i の終点と e_{i+1} の始点は一致する。
- e_k は頂点 N を終点とする。
ビット単位 \mathrm{XOR} 演算とは
非負整数 A, B のビット単位 \mathrm{XOR} 、A\ \mathrm{XOR}\ B は、以下のように定義されます。
- A\ \mathrm{XOR}\ B を二進表記した際の 2^k (k \geq 0) の位の数は、A, B を二進表記した際の 2^k の位の数のうち一方のみが 1 であれば 1、そうでなければ 0 である。
一般に k 個の非負整数 p_1, p_2, p_3, \dots, p_k のビット単位 \mathrm{XOR} は (\dots ((p_1\ \mathrm{XOR}\ p_2)\ \mathrm{XOR}\ p_3)\ \mathrm{XOR}\ \dots\ \mathrm{XOR}\ p_k) と定義され、これは p_1, p_2, p_3, \dots p_k の順番によらないことが証明できます。
制約
- 2 \leq N \leq 1000
- 0 \leq M \leq 1000
- 1 \leq A_i,B_i \leq N
- 0 \leq W_i < 2^{10}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 W_1 A_2 B_2 W_2 \vdots A_M B_M W_M
出力
頂点 1 から頂点 N への walk が存在しない場合、-1 と出力せよ。
頂点 1 から頂点 N への walk が存在する場合、そのうち、walk に含まれる辺の重みのビット単位 \mathrm{XOR} の最小値を出力せよ。
入力例 1
3 3 1 2 4 2 3 5 1 3 2
出力例 1
1
(辺 1, 辺 2) という walk に含まれる辺の重みのビット単位 \mathrm{XOR} は 1 となります。
入力例 2
4 4 1 4 7 4 2 2 2 3 4 3 4 1
出力例 2
0
(辺 1, 辺 2, 辺 3, 辺 4) という walk に含まれる辺の重みのビット単位 \mathrm{XOR} は 0 となります。
途中に頂点 N を含んでも良いことに注意してください。
入力例 3
999 4 1 2 9 2 1 8 1 2 7 1 1 6
出力例 3
-1
頂点 1 から頂点 N への walk が存在しない場合、-1 と出力してください。
Score : 400 points
Problem Statement
There is a directed graph with N vertices and M edges, where vertices are numbered from 1 to N and edges are numbered from 1 to M. Edge i is a directed edge from vertex A_i to vertex B_i with weight W_i.
Find the minimum value of the bitwise \mathrm{XOR} of the weights of edges included in a walk from vertex 1 to vertex N.
What is a walk from vertex 1 to vertex N?
Intuitively, it is "a path from vertex 1 to vertex N that may visit the same vertex or edge multiple times." Formally, it is a sequence of edges (e_1,\ldots,e_k) that satisfies all of the following conditions:
- e_1 starts at vertex 1.
- For all 1 \leq i < k, the endpoint of e_i and the starting point of e_{i+1} are the same.
- e_k ends at vertex N.
What is the bitwise \mathrm{XOR} operation?
The bitwise \mathrm{XOR} of non-negative integers A and B, denoted A\ \mathrm{XOR}\ B, is defined as follows:
- When A\ \mathrm{XOR}\ B is written in binary, the digit at the 2^k place (k \geq 0) is 1 if exactly one of the digits at the 2^k place of A and B in binary is 1, and 0 otherwise.
In general, the bitwise \mathrm{XOR} of k non-negative integers p_1, p_2, p_3, \dots, p_k is defined as (\dots ((p_1\ \mathrm{XOR}\ p_2)\ \mathrm{XOR}\ p_3)\ \mathrm{XOR}\ \dots\ \mathrm{XOR}\ p_k), and it can be proved that this does not depend on the order of p_1, p_2, p_3, \dots p_k.
Constraints
- 2 \leq N \leq 1000
- 0 \leq M \leq 1000
- 1 \leq A_i,B_i \leq N
- 0 \leq W_i < 2^{10}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 W_1 A_2 B_2 W_2 \vdots A_M B_M W_M
Output
If there is no walk from vertex 1 to vertex N, output -1.
If there is a walk from vertex 1 to vertex N, output the minimum value of the bitwise \mathrm{XOR} of the weights of edges included in such a walk.
Sample Input 1
3 3 1 2 4 2 3 5 1 3 2
Sample Output 1
1
The bitwise \mathrm{XOR} of the weights of edges included in the walk (edge 1, edge 2) is 1.
Sample Input 2
4 4 1 4 7 4 2 2 2 3 4 3 4 1
Sample Output 2
0
The bitwise \mathrm{XOR} of the weights of edges included in the walk (edge 1, edge 2, edge 3, edge 4) is 0.
Note that the walk may include vertex N in the middle.
Sample Input 3
999 4 1 2 9 2 1 8 1 2 7 1 1 6
Sample Output 3
-1
If there is no walk from vertex 1 to vertex N, output -1.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 450 点
問題文
高橋君が N 体のモンスターと順に戦うゲームで遊ぼうとしています。最初、高橋君の体力は H 、魔力は M です。
i 番目に戦うモンスターに対して、高橋君は以下のどちらかの行動を選べます。
- 魔法を使わずに戦う。体力が A_i 以上のときのみ選ぶことができ、体力が A_i 減少しモンスターを倒す。
- 魔法を使って戦う。魔力が B_i 以上のときのみ選ぶことができ、魔力が B_i 減少しモンスターを倒す。
N 体全てのモンスターを倒すか、高橋君が行動できなくなるとゲーム終了です。ゲーム終了までに最大で何体のモンスターを倒せますか。
制約
- 1 \leq N \leq 3000
- 1 \leq H,M \leq 3000
- 1 \leq A_i,B_i \leq 3000
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N H M A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
答えを出力せよ。
入力例 1
4 10 14 5 8 5 6 7 9 99 99
出力例 1
3
次のように行動することで、ゲーム終了までに 3 体のモンスターを倒すことができます。
- 最初、高橋君の体力は 10、魔力は 14 です。
- 1 体目のモンスターと魔法を使わずに戦う。体力が 5 減少し、体力が 5、魔力が 14 となる。
- 2 体目のモンスターと魔法を使わずに戦う。体力が 5 減少し、体力が 0、魔力が 14 となる。
- 3 体目のモンスターと魔法を使って戦う。魔力が 9 減少し、体力が 0、魔力が 5 となる。
- 4 体目のモンスターとの戦いではどちらの行動も選べないためゲーム終了となる。
入力例 2
3 3000 3000 3 3 3 3 3 3
出力例 2
3
全てのモンスターを倒せることもあります。
入力例 3
10 8 8 2 2 2 3 2 2 1 2 2 3 1 2 3 3 3 2 3 1 3 2
出力例 3
9
Score : 450 points
Problem Statement
Takahashi is about to play a game where he fights N monsters in order. Initially, Takahashi's health is H and his magic power is M.
For the i-th monster he fights, he can choose one of the following actions:
- Fight without using magic. This can only be chosen when his health is at least A_i, and his health decreases by A_i and the monster is defeated.
- Fight using magic. This can only be chosen when his magic power is at least B_i, and his magic power decreases by B_i and the monster is defeated.
The game ends when all N monsters are defeated or when he cannot take any action. What is the maximum number of monsters he can defeat before the game ends?
Constraints
- 1 \leq N \leq 3000
- 1 \leq H,M \leq 3000
- 1 \leq A_i,B_i \leq 3000
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N H M A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Output the answer.
Sample Input 1
4 10 14 5 8 5 6 7 9 99 99
Sample Output 1
3
By taking the following actions, Takahashi can defeat 3 monsters before the game ends.
- Initially, his health is 10 and his magic power is 14.
- Fight the 1st monster without using magic. His health decreases by 5, becoming health 5 and magic power 14.
- Fight the 2nd monster without using magic. His health decreases by 5, becoming health 0 and magic power 14.
- Fight the 3rd monster using magic. His magic power decreases by 9, becoming health 0 and magic power 5.
- For the 4th monster, he cannot choose either action, so the game ends.
Sample Input 2
3 3000 3000 3 3 3 3 3 3
Sample Output 2
3
He may be able to defeat all monsters.
Sample Input 3
10 8 8 2 2 2 3 2 2 1 2 2 3 1 2 3 3 3 2 3 1 3 2
Sample Output 3
9
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
H \times W のグリッドが与えられ、各マスには # か . のどちらかが書かれています。
各マスに書かれている記号の情報は H 個の長さ W の文字列 S_1,S_2,\dots,S_H として与えられ、上から i 行目、左から j 列目にあるマスには S_i の j 文字目と同じ記号が書かれています。
このグリッドに対し、以下の条件を全て満たす長方領域がいくつあるか求めてください。
- 長方領域に含まれる
#が書かれたマスの個数と.が書かれたマスの個数が等しい。
厳密には、次の条件を全て満たす 4 つの整数の組 (u,d,l,r) の数を求めてください。
- 1 \le u \le d \le H
- 1 \le l \le r \le W
- グリッドのうち上から u 行目から d 行目、左から l 列目から r 列目の部分を取り出す。このとき、取り出した部分に含まれる
#が書かれたマスの個数と.が書かれたマスの個数が等しい。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1 \le T \le 25000
- 1 \le H,W
- ひとつの入力に含まれる H \times W の総和は 3 \times 10^5 を超えない。
- S_i は
#と.からなる長さ W の文字列である。
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
\mathrm{case}_i は i 番目のテストケースを表す。 各テストケースは以下の形式で与えられる。
H W S_1 S_2 \vdots S_H
出力
T 行出力せよ。i 行目 には i 番目のテストケースに対する答えを出力せよ。
入力例 1
3 3 2 ## #. .. 6 6 ..#... ..#..# #.#.#. .###.. ###### .###.. 15 50 .......................#...........###.###.###.### ....................#..#..#..........#.#.#...#.#.. .................#...#####...#.....###.#.#.###.### ..................#..##.##..#......#...#.#.#.....# ...................#########.......###.###.###.### ....................#.....#....................... .###........##......#.....#..#...#.####.####.##..# #..#.........#......#.....#..#...#.#....#....##..# #..#.........#......#.....#..#...#.#....#....##..# #.....##...###..##..#.....#..#...#.#....#....#.#.# #....#..#.#..#.#..#.#..##.#..#...#.####.####.#.#.# #....#..#.#..#.####.#....##..#...#.#....#....#.#.# #....#..#.#..#.#....#.....#..#...#.#....#....#..## #..#.#..#.#..#.#..#.#....#.#.#...#.#....#....#..## .##...##...####.##...####..#..###..####.####.#..##
出力例 1
4 79 4032
この入力には 3 個のテストケースが含まれます。
1 番目のケースについて、以下の 4 個の長方領域が問題文中の条件を満たします。
- 上から 1 行目から 2 行目、左から 2 列目から 2 列目
- 上から 2 行目から 3 行目、左から 1 列目から 1 列目
- 上から 2 行目から 2 行目、左から 1 列目から 2 列目
- 上から 1 行目から 3 行目、左から 1 列目から 2 列目
Score : 525 points
Problem Statement
You are given an H \times W grid, where each cell contains # or ..
The information about the symbols written in each cell is given as H strings S_1,S_2,\dots,S_H of length W, where the cell in the i-th row from the top and j-th column from the left contains the same symbol as the j-th character of S_i.
Find the number of rectangular regions in this grid that satisfy all of the following conditions:
- The number of cells containing
#and the number of cells containing.in the rectangular region are equal.
Formally, find the number of quadruples of integers (u,d,l,r) that satisfy all of the following conditions:
- 1 \le u \le d \le H
- 1 \le l \le r \le W
- When extracting the part of the grid from the u-th through d-th rows from the top and from the l-th through r-th columns from the left, the number of cells containing
#and the number of cells containing.in the extracted part are equal.
You are given T test cases. Find the answer for each of them.
Constraints
- 1 \le T \le 25000
- 1 \le H,W
- The sum of H \times W over all test cases in one input does not exceed 3 \times 10^5.
- S_i is a string of length W consisting of
#and..
Input
The input is given from Standard Input in the following format:
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
\mathrm{case}_i represents the i-th test case. Each test case is given in the following format:
H W S_1 S_2 \vdots S_H
Output
Output T lines. The i-th line should contain the answer for the i-th test case.
Sample Input 1
3 3 2 ## #. .. 6 6 ..#... ..#..# #.#.#. .###.. ###### .###.. 15 50 .......................#...........###.###.###.### ....................#..#..#..........#.#.#...#.#.. .................#...#####...#.....###.#.#.###.### ..................#..##.##..#......#...#.#.#.....# ...................#########.......###.###.###.### ....................#.....#....................... .###........##......#.....#..#...#.####.####.##..# #..#.........#......#.....#..#...#.#....#....##..# #..#.........#......#.....#..#...#.#....#....##..# #.....##...###..##..#.....#..#...#.#....#....#.#.# #....#..#.#..#.#..#.#..##.#..#...#.####.####.#.#.# #....#..#.#..#.####.#....##..#...#.#....#....#.#.# #....#..#.#..#.#....#.....#..#...#.#....#....#..## #..#.#..#.#..#.#..#.#....#.#.#...#.#....#....#..## .##...##...####.##...####..#..###..####.####.#..##
Sample Output 1
4 79 4032
This input contains 3 test cases.
For the 1st case, the following 4 rectangular regions satisfy the conditions in the problem statement:
- From the 1st to 2nd rows from the top, from the 2nd to 2nd columns from the left
- From the 2nd to 3rd rows from the top, from the 1st to 1st columns from the left
- From the 2nd to 2nd rows from the top, from the 1st to 2nd columns from the left
- From the 1st to 3rd rows from the top, from the 1st to 2nd columns from the left
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 575 点
問題文
円周上に 1 から 2N の番号がついた相異なる 2N 個の点があり、点 1 から時計回りに順に点 2、点 3、…、点 2N と並んでいます。
この円の弦が N 個与えられます。i 番目の弦の端点は点 A_i と点 B_i であり、2N 個の値 A_1,\ldots,A_N,B_1,\ldots,B_N は相異なります。
この円に対し以下の操作を一度ずつ順に行います。
- 円の N 本の弦のうち、互いに交わらないように弦を好きな個数選び、残りの弦を削除する。
- 円に自由に弦を 1 つ追加する。
適切に操作を行ったとき、操作を終えた後の弦同士の交点の個数として考えられる最大値を求めてください。
制約
- 1 \leq N \leq 2\times 10^5
- 1 \leq A_i,B_i \leq 2N
- 2N 個の値 A_1, \ldots, A_N,B_1,\ldots,B_N は相異なる
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
答えを出力せよ。
入力例 1
3 1 5 6 3 4 2
出力例 1
2
最初、円には弦が 3 本あり、図のようになっています。
操作により点 3 と点 6 を結ぶ弦を削除し、新たな弦を追加することで、弦同士の交点の個数は 2 個となります。
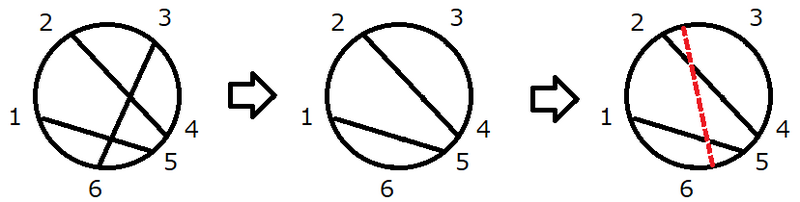
弦同士の交点の個数を 3 個以上にすることはできないため、答えは 2 となります。
最後に追加する弦の端点は、点 1,\ldots, 2N のいずれかである必要はありません。
入力例 2
4 1 8 2 7 3 6 4 5
出力例 2
4
入力例 3
3 1 2 3 4 5 6
出力例 3
2
Score : 575 points
Problem Statement
There are 2N pairwise distinct points, numbered from 1 to 2N, on a circle. Starting from point 1 and going clockwise, the points are arranged as point 2, point 3, ..., point 2N.
You are given N chords on this circle. The endpoints of the i-th chord are points A_i and B_i, and the 2N values A_1,\ldots,A_N,B_1,\ldots,B_N are all distinct.
Perform the following operations on this circle once each in order:
- Among the N chords on the circle, choose any number of chords such that no two chosen chords intersect, and delete the remaining chords.
- Add one chord freely to the circle.
Find the maximum possible number of intersection points between chords after the operations are completed.
Constraints
- 1 \leq N \leq 2\times 10^5
- 1 \leq A_i,B_i \leq 2N
- The 2N values A_1, \ldots, A_N,B_1,\ldots,B_N are pairwise distinct.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Output the answer.
Sample Input 1
3 1 5 6 3 4 2
Sample Output 1
2
Initially, there are 3 chords on the circle, as shown in the figure.
After deleting the chord connecting points 3 and 6 and adding a new chord through the operations, the number of intersection points between chords is 2.

It is impossible to make the number of intersection points between chords 3 or more, so the answer is 2.
The endpoints of the chord added at the end do not need to be any of the points 1,\ldots, 2N.
Sample Input 2
4 1 8 2 7 3 6 4 5
Sample Output 2
4
Sample Input 3
3 1 2 3 4 5 6
Sample Output 3
2