実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
8 種類の方角(北、東、西、南、北東、北西、南東、南西)のいずれかを表す文字列 D が与えられます。方角とそれを表す文字列は以下のように対応しています。
- 北:
N - 東:
E - 西:
W - 南:
S - 北東:
NE - 北西:
NW - 南東:
SE - 南西:
SW
D が表す方角の反対の方角を表す文字列を出力してください。
制約
- D は
N,E,W,S,NE,NW,SE,SWのいずれか
入力
入力は以下の形式で標準入力から与えられる。
D
出力
答えを出力せよ。
入力例 1
N
出力例 1
S
北の反対の方角である南を表す S を出力してください。
入力例 2
SE
出力例 2
NW
南東の反対の方角である北西を表す NW を出力してください。
Score : 100 points
Problem Statement
You are given a string D representing one of the eight directions (north, east, west, south, northeast, northwest, southeast, southwest). The correspondence between the directions and their representing strings is as follows.
- North:
N - East:
E - West:
W - South:
S - Northeast:
NE - Northwest:
NW - Southeast:
SE - Southwest:
SW
Print the string representing the direction opposite to the direction denoted by D.
Constraints
- D is one of
N,E,W,S,NE,NW,SE,SW.
Input
The input is given from Standard Input in the following format:
D
Output
Print the answer.
Sample Input 1
N
Sample Output 1
S
Print S, which represents south, the direction opposite to north.
Sample Input 2
SE
Sample Output 2
NW
Print NW, which represents northwest, the direction opposite to southeast.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
N \times N のグリッド S と M\times M のグリッド T が与えられます。上から i 行目、左から j 列目のマス目をマス (i,j) と表します。
S,T の各マスの色はそれぞれ N^2個の文字 S_{i,j} \; (1\leq i,j\leq N) および M^2 個の文字 T_{i,j} \; (1\leq i,j\leq M) によって表されます。
S_{i,j} が . のとき S のマス (i,j) は白色、S_{i,j} が # のとき S のマス (i,j) は黒色で塗られています。T についても同様です。
S の中から T を探してください。具体的には、以下の条件を満たす a,b \; (1 \leq a,b \leq N-M+1) を出力してください。
- すべての i,j \; (1\leq i,j \leq M) について、S_{a+i-1,b+j-1} = T_{i,j}
制約
- 1 \leq M \leq N \leq 50
- N,M は整数
- S_{i,j},T_{i,j} は
.または# - 条件を満たす a,b はちょうど 1 組存在する。
入力
入力は以下の形式で標準入力から与えられる。
N M
S_{1,1}S_{1,2}\dots S_{1,N}
S_{2,1}S_{2,2}\dots S_{2,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,M}
T_{2,1}T_{2,2}\dots T_{2,M}
\vdots
T_{M,1}T_{M,2}\dots T_{M,M}
出力
a,b をこの順に空白区切りで 1 行に出力せよ。
入力例 1
3 2 #.# ..# ##. .# #.
出力例 1
2 2
S の 2 行目から 3 行目、2 列目から 3 列目の 2 \times 2 マスが T と一致します。
入力例 2
2 1 #. ## .
出力例 2
1 2
Score : 200 points
Problem Statement
You are given an N \times N grid S and an M \times M grid T. The cell at the i-th row from the top and the j-th column from the left is denoted by (i,j).
The colors of the cells in S and T are represented by N^2 characters S_{i,j} (1\leq i,j\leq N) and M^2 characters T_{i,j} (1\leq i,j\leq M), respectively. In grid S, cell (i,j) is white if S_{i,j} is ., and black if S_{i,j} is #. The same applies for grid T.
Find T within S. More precisely, output integers a and b (1 \leq a,b \leq N-M+1) that satisfy the following condition:
- S_{a+i-1,b+j-1} = T_{i,j} for every i,j (1\leq i,j \leq M).
Constraints
- 1 \leq M \leq N \leq 50
- N and M are integers.
- Each of S_{i,j} and T_{i,j} is
.or#. - There is exactly one pair (a,b) satisfying the condition.
Input
The input is given from Standard Input in the following format:
N M
S_{1,1}S_{1,2}\dots S_{1,N}
S_{2,1}S_{2,2}\dots S_{2,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,M}
T_{2,1}T_{2,2}\dots T_{2,M}
\vdots
T_{M,1}T_{M,2}\dots T_{M,M}
Output
Print a and b in this order, separated by a space on one line.
Sample Input 1
3 2 #.# ..# ##. .# #.
Sample Output 1
2 2
The 2 \times 2 subgrid of S from the 2nd to the 3rd row and from the 2nd to the 3rd column matches T.
Sample Input 2
2 1 #. ## .
Sample Output 2
1 2
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
N 匹の鳩がおり、 1 から N までの番号がつけられています。また、 N 個の巣があり、 1 から N までの番号がつけられています。はじめ、鳩 i は巣 i にいます (1\leq i\leq N)。
Q 個のクエリが与えられるので順に処理してください。 クエリは 2 種類あり、以下のいずれかの形式で与えられます。
1 P H: 鳩 P を巣 H に移動させる。2: 複数の鳩がいる巣の個数を出力する。
制約
- 2\leq N\leq 10^6
- 1\leq Q\leq 3\times 10^5
- 1\leq P,H\leq N
- 1 つ目の形式のクエリについて、鳩 P は移動する前に巣 H にいない
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
各クエリは以下の 2 種類のいずれかの形式で与えられる。
1 P H
2
出力
問題文の指示に従ってクエリへの答えを改行区切りで出力せよ。
入力例 1
4 7 2 1 1 2 2 1 3 2 2 1 3 4 2
出力例 1
0 1 1 2
初め、鳩 1,2,3,4 はそれぞれ巣 1,2,3,4 にいます。
- 1 つ目のクエリについて、巣 1,2,3,4 にはそれぞれ 1,1,1,1 匹います。鳩が複数いる巣は存在しないので 0 を出力します。
- 2 つ目のクエリについて、鳩 1 を巣 2 に移動します。
- 3 つ目のクエリについて、巣 1,2,3,4 にはそれぞれ 0,2,1,1 匹います。鳩が複数いる巣は巣 2 の 1 つなので 1 を出力します。
- 4 つ目のクエリについて、鳩 3 を巣 2 に移動します。
- 5 つ目のクエリについて、巣 1,2,3,4 にはそれぞれ 0,3,0,1 匹います。鳩が複数いる巣は巣 2 の 1 つなので 1 を出力します。
- 6 つ目のクエリについて、鳩 3 を巣 4 に移動します。
- 7 つ目のクエリについて、巣 1,2,3,4 にはそれぞれ 0,2,0,2 匹います。鳩が複数いる巣は巣 2,4 の 2 つなので 2 を出力します。
入力例 2
5 10 2 1 4 3 1 4 5 2 1 3 1 2 1 2 3 1 2 5 1 1 3 2
出力例 2
0 1 2 1
Score : 300 points
Problem Statement
There are N pigeons numbered from 1 to N, and there are N nests numbered from 1 to N. Initially, pigeon i is in nest i for 1\leq i\leq N.
You are given Q queries, which you must process in order. There are two types of queries, each given in one of the following formats:
1 P H: Move pigeon P to nest H.2: Output the number of nests that contain more than one pigeon.
Constraints
- 2 \leq N \leq 10^6
- 1 \leq Q \leq 3\times 10^5
- 1 \leq P, H \leq N
- For a query of the first type, pigeon P is not in nest H before the move.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
Each query is given in one of the following two formats:
1 P H
2
Output
Print the answer to each query on a new line according to the instructions in the problem statement.
Sample Input 1
4 7 2 1 1 2 2 1 3 2 2 1 3 4 2
Sample Output 1
0 1 1 2
Initially, pigeons 1,2,3,4 are in nests 1,2,3,4, respectively.
- For the 1st query, the counts of pigeons in nests 1,2,3,4 are 1,1,1,1. No nests contain multiple pigeons, output 0.
- For the 2nd query, move pigeon 1 to nest 2.
- For the 3rd query, the counts become 0,2,1,1, respectively. One nest (nest 2) contains multiple pigeons, so output 1.
- For the 4th query, move pigeon 3 to nest 2.
- For the 5th query, the counts become 0,3,0,1, respectively. One nest (nest 2) contains multiple pigeons, so output 1.
- For the 6th query, move pigeon 3 to nest 4.
- For the 7th query, the counts become 0,2,0,2, respectively. Two nests (nests 2 and 4) contain multiple pigeons, so output 2.
Sample Input 2
5 10 2 1 4 3 1 4 5 2 1 3 1 2 1 2 3 1 2 5 1 1 3 2
Sample Output 2
0 1 2 1
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
10^9 行 W 列のグリッドがあります。左から x 列目、下から y 行目のマスを (x,y) と表します。
N 個のブロックがあります。各ブロックは 1 \times 1 の正方形で、ブロック i (1 \leq i \leq N) は時刻 0 にマス (X_i,Y_i) にあります。
時刻 t=1,2,\dots,10^{100} に、以下のルールに従ってブロックを動かします。
- グリッドの下から 1 行目がすべてブロックで埋まっているならば、下から 1 行目にあるブロックをすべて消滅させる。
- 残っているブロックについて、下にあるブロックから順番に、以下の操作を行う。
- ブロックが一番下の行にある、またはそのブロックの 1 つ下のマスにもブロックがあるならば、何もしない
- そうでなければ、ブロックを 1 つ下のマスに動かす。
Q 個の質問が与えられます。j 番目 (1 \leq j \leq Q) の質問では、時刻 T_j+0.5 にブロック A_j が存在するかどうか答えてください。
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq W \leq N
- 1 \leq X_i \leq W
- 1 \leq Y_i \leq 10^9
- i \neq j なら (X_i,Y_i) \neq (X_j,Y_j)
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_j \leq 10^9
- 1 \leq A_j \leq N
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N Q T_1 A_1 T_2 A_2 \vdots T_Q A_Q
出力
Q 行出力せよ。i 行目には、時刻 T_i+0.5 にブロック A_i が存在するならば Yes を、存在しないならば No を出力せよ。
入力例 1
5 3 1 1 1 2 2 2 3 2 2 3 6 1 1 1 2 2 3 2 5 3 4 3 5
出力例 1
Yes Yes No Yes No Yes
ブロックの位置は以下のように変化します。
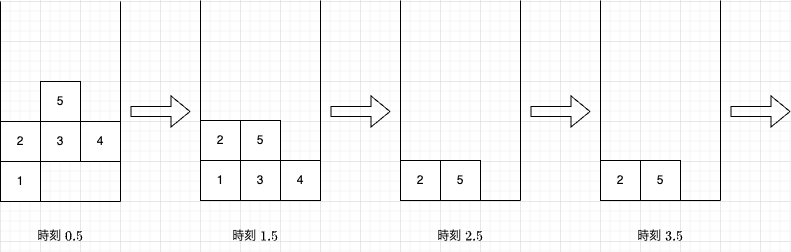
- 質問 1: 時刻 1.5 にブロック 1 は存在するので、答えは
Yesです。 - 質問 2: 時刻 1.5 にブロック 2 は存在するので、答えは
Yesです。 - 質問 3: ブロック 3 は時刻 2 に消滅します。よって、時刻 2.5 にブロック 3 は存在しないので、答えは
Noです。
入力例 2
3 2 1 1 2 1 1 2 4 1 1 1 2 1 3 2 3
出力例 2
No No Yes Yes
Score : 400 points
Problem Statement
There is a grid with 10^9 rows and W columns. The cell at the x-th column from the left and the y-th row from the bottom is denoted by (x,y).
There are N blocks. Each block is a 1 \times 1 square, and block i-th (1 \leq i \leq N) is located at cell (X_i,Y_i) at time 0.
At times t=1,2,\dots,10^{100}, the blocks are moved according to the following rules:
- If the entire bottom row is filled with blocks, then all blocks in the bottom row are removed.
- For each remaining block, in order from bottom to top, perform the following:
- If the block is in the bottom row, or if there is a block in the cell immediately below it, do nothing.
- Otherwise, move the block one cell downward.
You are given Q queries. For the j-th query (1 \leq j \leq Q), answer whether block A_j exists at time T_j+0.5.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq W \leq N
- 1 \leq X_i \leq W
- 1 \leq Y_i \leq 10^9
- (X_i,Y_i) \neq (X_j,Y_j) if i \neq j.
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_j \leq 10^9
- 1 \leq A_j \leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N Q T_1 A_1 T_2 A_2 \vdots T_Q A_Q
Output
Print Q lines. The i-th line should contain Yes if block A_i exists at time T_i+0.5, and No otherwise.
Sample Input 1
5 3 1 1 1 2 2 2 3 2 2 3 6 1 1 1 2 2 3 2 5 3 4 3 5
Sample Output 1
Yes Yes No Yes No Yes
The positions of the blocks change as follows: ("時刻" means "time.")

- Query 1: At time 1.5, block 1 exists, so the answer is
Yes. - Query 2: At time 1.5, block 2 exists, so the answer is
Yes. - Query 3: Block 3 disappears at time 2, so it does not exist at time 2.5, and the answer is
No.
Sample Input 2
3 2 1 1 2 1 1 2 4 1 1 1 2 1 3 2 3
Sample Output 2
No No Yes Yes
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 450 点
問題文
長さ 3^n \; (n \geq 1) の 01 列 B=B_1 B_2 \dots B_{3^n} に対して、長さ 3^{n-1} の 01 列 C=C_1 C_2 \dots C_{3^{n-1}} を得る操作を以下のように定めます。
- B の要素を 3 つずつまとめて多数決を取る。すなわち、i=1,2,\dots,3^{n-1} について、B_{3i-2},B_{3i-1},B_{3i} のうち最も多く現れる値を C_i とする。
長さ 3^N の 01 列 A = A_1 A_2 \dots A_{3^N} が与えられます。A に上の操作を N 回適用して得られる長さ 1 の列を A' = A'_1 とします。
A の要素のいくつかを 0 から 1 または 1 から 0 へ変えることを考えたとき、A の要素を最小で何個変えれば、A'_1 の値が変わるか求めてください。
制約
- N は 1 以上 13 以下の整数
- A は 0,1 からなる長さ 3^N の文字列
入力
入力は以下の形式で標準入力から与えられる。
N
A_1 A_2 \dots A_{3^N}
出力
答えを出力せよ。
入力例 1
2 010011101
出力例 1
1
A=010011101 に操作を 2 回適用すると、以下のようになります。
- 1 回目: 010 の過半数は 0, 011 の過半数は 1, 101 の過半数は 1 なので、これらをつなげて 011 を得る。
- 2 回目: 011 の過半数は 1 なので、 1 を得る。
最終的な値を 1 から 0 にするためには、例えば A の 5 文字目を 1 から 0 にして A=010001101 にすればよいです。変更後、操作は以下のようになります。
- 1 回目: 010 の過半数は 0, 001 の過半数は 0, 101 の過半数は 1 なので、これらをつなげて 001 を得る。
- 2 回目: 001 の過半数は 0 なので、 0 を得る。
よって、 A の要素を 1 個変えるのが最小です。
入力例 2
1 000
出力例 2
2
Score : 450 points
Problem Statement
For a binary string B = B_1 B_2 \dots B_{3^n} of length 3^n (n \geq 1), we define an operation to obtain a binary string C = C_1 C_2 \dots C_{3^{n-1}} of length 3^{n-1} as follows:
- Partition the elements of B into groups of 3 and take the majority value from each group. That is, for i=1,2,\dots,3^{n-1}, let C_i be the value that appears most frequently among B_{3i-2}, B_{3i-1}, and B_{3i}.
You are given a binary string A = A_1 A_2 \dots A_{3^N} of length 3^N. Let A' = A'_1 be the length-1 string obtained by applying the above operation N times to A.
Determine the minimum number of elements of A that must be changed (from 0 to 1 or from 1 to 0) in order to change the value of A'_1.
Constraints
- N is an integer with 1 \leq N \leq 13.
- A is a string of length 3^N consisting of 0 and 1.
Input
The input is given from Standard Input in the following format:
N
A_1 A_2 \dots A_{3^N}
Output
Print the answer.
Sample Input 1
2 010011101
Sample Output 1
1
For example, with A=010011101, after applying the operation twice, we obtain:
- First operation: The majority of 010 is 0, of 011 is 1, and of 101 is 1, resulting in 011.
- Second operation: The majority of 011 is 1, yielding 1.
To change the final value from 1 to 0, one way is to change the 5th character of A from 1 to 0, yielding A=010001101. After the change, the operations yield:
- First operation: The majority of 010 is 0, of 001 is 0, and of 101 is 1, resulting in 001.
- Second operation: The majority of 001 is 0, yielding 0.
Thus, the minimum number of changes required is 1.
Sample Input 2
1 000
Sample Output 2
2
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
長さ N の整数列 A=(A_1,A_2,\ldots,A_N), B=(B_1,B_2,\ldots,B_N),C=(C_1,C_2,\ldots,C_N) および整数 K が与えられます。
1\leq i,j,k\leq N を満たす整数 i,j,k の選び方 N^3 通りそれぞれに対して A_iB_j+B_jC_k+C_kA_i の値を計算したとき、その中で大きい方から K 番目の値を求めてください。
制約
- 1\leq N\leq 2\times 10^5
- 1\leq K\leq \min(N^3,5\times 10^5)
- 1\leq A_i,B_i,C_i\leq 10^9
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N K A_1 A_2 \ldots A_N B_1 B_2 \ldots B_N C_1 C_2 \ldots C_N
出力
答えを出力せよ。
入力例 1
2 5 1 2 3 4 5 6
出力例 1
31
N^3=8 個の整数の値は以下の通りです。
- (i,j,k)=(1,1,1) : A_1B_1+B_1C_1+C_1A_1=1\times 3+3\times 5+5\times 1=23
- (i,j,k)=(1,1,2) : A_1B_1+B_1C_2+C_2A_1=1\times 3+3\times 6+6\times 1=27
- (i,j,k)=(1,2,1) : A_1B_2+B_2C_1+C_1A_1=1\times 4+4\times 5+5\times 1=29
- (i,j,k)=(1,2,2) : A_1B_2+B_2C_2+C_2A_1=1\times 4+4\times 6+6\times 1=34
- (i,j,k)=(2,1,1) : A_2B_1+B_1C_1+C_1A_2=2\times 3+3\times 5+5\times 2=31
- (i,j,k)=(2,1,2) : A_2B_1+B_1C_2+C_2A_2=2\times 3+3\times 6+6\times 2=36
- (i,j,k)=(2,2,1) : A_2B_2+B_2C_1+C_1A_2=2\times 4+4\times 5+5\times 2=38
- (i,j,k)=(2,2,2) : A_2B_2+B_2C_2+C_2A_2=2\times 4+4\times 6+6\times 2=44
これらを値の降順に並べ替えると (44,38,36,34,31,29,27,23) となるため、 大きい方から 5 番目の値は 31 です。
入力例 2
3 10 100 100 100 100 100 100 100 100 100
出力例 2
30000
入力例 3
5 54 800516877 573289179 26509423 168629803 696409999 656737335 915059758 201458890 931198638 185928366 140174496 254538849 830992027 305186313 322164559
出力例 3
689589940713840351
Score : 500 points
Problem Statement
You are given three integer sequences of length N, namely A=(A_1,A_2,\ldots,A_N), B=(B_1,B_2,\ldots,B_N), and C=(C_1,C_2,\ldots,C_N), and an integer K.
For each of the N^3 choices of integers i,j,k (1\leq i,j,k\leq N), compute the value A_iB_j + B_jC_k + C_kA_i. Among all these values, find the K-th largest value.
Constraints
- 1\leq N \leq 2\times 10^5
- 1\leq K \leq \min(N^3,5\times 10^5)
- 1\leq A_i,B_i,C_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N K A_1 A_2 \ldots A_N B_1 B_2 \ldots B_N C_1 C_2 \ldots C_N
Output
Print the answer.
Sample Input 1
2 5 1 2 3 4 5 6
Sample Output 1
31
The N^3=8 values are computed as follows:
- For (i,j,k)=(1,1,1): A_1B_1+B_1C_1+C_1A_1=1\times 3+3\times 5+5\times 1=23
- For (i,j,k)=(1,1,2): A_1B_1+B_1C_2+C_2A_1=1\times 3+3\times 6+6\times 1=27
- For (i,j,k)=(1,2,1): A_1B_2+B_2C_1+C_1A_1=1\times 4+4\times 5+5\times 1=29
- For (i,j,k)=(1,2,2): A_1B_2+B_2C_2+C_2A_1=1\times 4+4\times 6+6\times 1=34
- For (i,j,k)=(2,1,1): A_2B_1+B_1C_1+C_1A_2=2\times 3+3\times 5+5\times 2=31
- For (i,j,k)=(2,1,2): A_2B_1+B_1C_2+C_2A_2=2\times 3+3\times 6+6\times 2=36
- For (i,j,k)=(2,2,1): A_2B_2+B_2C_1+C_1A_2=2\times 4+4\times 5+5\times 2=38
- For (i,j,k)=(2,2,2): A_2B_2+B_2C_2+C_2A_2=2\times 4+4\times 6+6\times 2=44
Sorting these values in descending order, we have (44,38,36,34,31,29,27,23), so the 5th largest value is 31.
Sample Input 2
3 10 100 100 100 100 100 100 100 100 100
Sample Output 2
30000
Sample Input 3
5 54 800516877 573289179 26509423 168629803 696409999 656737335 915059758 201458890 931198638 185928366 140174496 254538849 830992027 305186313 322164559
Sample Output 3
689589940713840351
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
長さ N の英小文字列 S および整数 M が与えられます。各 k=0,1,\ldots,N に対して以下の問題を解いてください。
- 長さ M の英小文字列は 26^M 通りあるが、そのうち S との最長共通部分列の長さが k であるようなものの個数を 998244353 で割った余りを求めよ。
制約
- 1\leq N\leq 10
- 1\leq M\leq 100
- N,M は整数
- S は長さ N の英小文字列
入力
入力は以下の形式で標準入力から与えられる。
N M S
出力
k=i のときの答えを \mathrm{ans}_i として、以下の形式で出力せよ。
\mathrm{ans}_0 \mathrm{ans}_1 \ldots \mathrm{ans}_N
入力例 1
2 2 ab
出力例 1
576 99 1
k=0,1,2 それぞれに対する答えは以下のようになります。
- k=0 : 長さ 2 の英小文字列のうち
abとの最長共通部分列が 0 であるようなものはcd,re,zzなど全部で 576 個存在します。 - k=1 : 長さ 2 の英小文字列のうち
abとの最長共通部分列が 1 であるようなものはac,wa,baなど全部で 99 個存在します。 - k=2 : 長さ 2 の英小文字列のうち
abとの最長共通部分列が 2 であるようなものはabの 1 個存在します。
入力例 2
3 4 aaa
出力例 2
390625 62500 3750 101
入力例 3
7 50 atcoder
出力例 3
309810541 226923474 392073062 146769908 221445233 435648037 862664208 238437587
Score : 600 points
Problem Statement
You are given a lowercase English string S of length N and an integer M. For each k=0,1,\ldots,N, solve the following problem:
- There are 26^M lowercase English strings of length M. Among these, find the number, modulo 998244353, of strings whose longest common subsequence with S has length exactly k.
Constraints
- 1\leq N\leq 10
- 1\leq M\leq 100
- N and M are integers.
- S is a lowercase English string of length N.
Input
The input is given from Standard Input in the following format:
N M S
Output
Let \mathrm{ans}_i be the answer for k=i. Print the answers in the following format:
\mathrm{ans}_0 \mathrm{ans}_1 \ldots \mathrm{ans}_N
Sample Input 1
2 2 ab
Sample Output 1
576 99 1
The answers for k=0,1,2 are as follows:
- For k=0: Among length 2 lowercase English strings, those with a longest common subsequence of length 0 with
abinclude strings such ascd,re,zz, totaling 576. - For k=1: Among length 2 lowercase English strings, those with a longest common subsequence of length 1 with
abinclude strings such asac,wa,ba, totaling 99. - For k=2: Among length 2 lowercase English strings, there is 1 string (
ab) whose longest common subsequence withabhas length 2.
Sample Input 2
3 4 aaa
Sample Output 2
390625 62500 3750 101
Sample Input 3
7 50 atcoder
Sample Output 3
309810541 226923474 392073062 146769908 221445233 435648037 862664208 238437587