Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
3 つの整数 A,B,C が与えられます。これら 3 つの整数を 2 つ以上のグループに分けて、それぞれのグループ内の数の和を等しくできるかどうか判定してください。
制約
- 1 \leq A,B,C \leq 1000
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
A B C
出力
A,B,C を和の等しい 2 つ以上のグループに分けることができるならば Yes を、できないならば No を出力せよ。
入力例 1
3 8 5
出力例 1
Yes
例えば、(3,5),(8) と 2 つのグループに分けることで、それぞれのグループ内の和をどちらも 8 にすることができます。
入力例 2
2 2 2
出力例 2
Yes
(2),(2),(2) と 3 つのグループに分けることで、それぞれのグループ内の和をどれも 2 にすることができます。
入力例 3
1 2 4
出力例 3
No
どのように 2 つ以上のグループに分けても、和を等しくすることはできません。
Score : 100 points
Problem Statement
You are given three integers A,B,C. Determine whether it is possible to divide these three integers into two or more groups so that these groups have equal sums.
Constraints
- 1 \leq A,B,C \leq 1000
- All input values are integers.
Input
The input is given from Standard Input in the following format:
A B C
Output
If it is possible to divide A,B,C into two or more groups with equal sums, print Yes; otherwise, print No.
Sample Input 1
3 8 5
Sample Output 1
Yes
For example, by dividing into two groups (3,5) and (8), each group can have the sum 8.
Sample Input 2
2 2 2
Sample Output 2
Yes
By dividing into three groups (2),(2),(2), each group can have the sum 2.
Sample Input 3
1 2 4
Sample Output 3
No
No matter how you divide them into two or more groups, it is not possible to make the sums equal.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
縦 H 行横 W 列のマス目があります。上から i 行目、左から j 列目のマスをマス (i,j) と表します。
マス (i,j) は S_{i,j} が # のとき通行不可能、. のとき通行可能であり家が建っていない、@ のとき通行可能であり家が建っていることを表します。
最初、マス (X,Y) にサンタクロースがいます。サンタクロースは文字列 T に従って以下の行動を行います。
- 文字列 T の長さを |T| とする。i=1,2,\ldots,|T| の順に以下のように移動する。
- 現在サンタクロースがいるマスを (x,y) とする。
- T_i が
Uかつマス (x-1,y) が通行可能ならマス (x-1,y) に移動する。 - T_i が
Dかつマス (x+1,y) が通行可能ならマス (x+1,y) に移動する。 - T_i が
Lかつマス (x,y-1) が通行可能ならマス (x,y-1) に移動する。 - T_i が
Rかつマス (x,y+1) が通行可能ならマス (x,y+1) に移動する。 - それ以外の場合、マス (x,y) に留まる。
- T_i が
- 現在サンタクロースがいるマスを (x,y) とする。
行動を終えたあとにサンタクロースがいるマスと、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。
制約
- 3 \leq H,W \leq 100
- 1 \leq X \leq H
- 1 \leq Y \leq W
- 与えられる数値は全て整数である
- S_{i,j} は
#,.,@のいずれか - 全ての 1 \leq i \leq H について S_{i,1},S_{i,W} は
# - 全ての 1 \leq j \leq W について S_{1,j},S_{H,j} は
# - S_{X,Y}=
. - T は
U,D,L,Rのいずれかからなる長さ 1 以上 10^4 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
H W X Y
S_{1,1}S_{1,2}\ldots S_{1,W}
\dots
S_{H,1}S_{H,2}\ldots S_{H,W}
T
出力
行動を終えたあとサンタクロースがいるマスを (X,Y)、行動により通過または到達した家の数を C とするとき、X,Y,C をこの順に空白区切りで出力せよ。
入力例 1
5 5 3 4 ##### #...# #.@.# #..@# ##### LLLDRUU
出力例 1
2 3 1
サンタクロースは以下のように行動します。
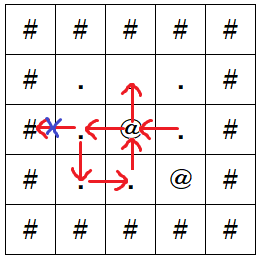
- T_1=
Lなのでマス (3,4) からマス (3,3) に移動する。これにより家を通過する。 - T_2=
Lなのでマス (3,3) からマス (3,2) に移動する。 - T_3=
Lだがマス (3,1) は通行不可能なので、マス (3,2) に留まる。 - T_4=
Dなのでマス (3,2) からマス (4,2) に移動する。 - T_5=
Rなのでマス (4,2) からマス (4,3) に移動する。 - T_6=
Uなのでマス (4,3) からマス (3,3) に移動する。これにより家を通過するが、この家はすでに通過したことがある家である。 - T_7=
Uなのでマス (3,3) からマス (2,3) に移動する。
行動により通過または到達した家の数は 1 です。
入力例 2
6 13 4 6 ############# #@@@@@@@@@@@# #@@@@@@@@@@@# #@@@@.@@@@@@# #@@@@@@@@@@@# ############# UURUURLRLUUDDURDURRR
出力例 2
3 11 11
入力例 3
12 35 7 10 ################################### #.................................# #..........@......................# #......@................@.........# #.............##............@.....# #...##........##....##............# #...##........##....##.......##...# #....##......##......##....##.....# #....##......##......##..##.......# #.....#######.........###.........# #.................................# ################################### LRURRRUUDDULUDUUDLRLRDRRLULRRUDLDRU
出力例 3
4 14 1
Score : 200 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
If S_{i,j} is #, the cell (i,j) is impassable; if it is ., the cell is passable and contains no house; if it is @, the cell is passable and contains a house.
Initially, Santa Claus is in cell (X,Y). He will act according to the string T as follows.
- Let |T| be the length of the string T. For i=1,2,\ldots,|T|, he moves as follows.
- Let (x,y) be the cell he is currently in.
- If T_i is
Uand cell (x-1,y) is passable, move to cell (x-1,y). - If T_i is
Dand cell (x+1,y) is passable, move to cell (x+1,y). - If T_i is
Land cell (x,y-1) is passable, move to cell (x,y-1). - If T_i is
Rand cell (x,y+1) is passable, move to cell (x,y+1). - Otherwise, stay in cell (x,y).
- If T_i is
- Let (x,y) be the cell he is currently in.
Find the cell where he is after completing all actions, and the number of distinct houses that he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.
Constraints
- 3 \leq H,W \leq 100
- 1 \leq X \leq H
- 1 \leq Y \leq W
- All given numbers are integers.
- Each S_{i,j} is one of
#,.,@. - S_{i,1} and S_{i,W} are
#for every 1 \leq i \leq H. - S_{1,j} and S_{H,j} are
#for every 1 \leq j \leq W. - S_{X,Y}=
. - T is a string of length at least 1 and at most 10^4, consisting of
U,D,L,R.
Input
The Input is given from Standard Input in the following format:
H W X Y
S_{1,1}S_{1,2}\ldots S_{1,W}
\dots
S_{H,1}S_{H,2}\ldots S_{H,W}
T
Output
Let (X,Y) be the cell where he is after completing all actions, and C be the number of distinct houses he passed through or arrived at during his actions. Print X,Y,C in this order separated by spaces.
Sample Input 1
5 5 3 4 ##### #...# #.@.# #..@# ##### LLLDRUU
Sample Output 1
2 3 1
Santa Claus behaves as follows:

- T_1=
L, so he moves from (3,4) to (3,3). A house is passed. - T_2=
L, so he moves from (3,3) to (3,2). - T_3=
L, but cell (3,1) is impassable, so he stays at (3,2). - T_4=
D, so he moves from (3,2) to (4,2). - T_5=
R, so he moves from (4,2) to (4,3). - T_6=
U, so he moves from (4,3) to (3,3). A house is passed, but it has already been passed. - T_7=
U, so he moves from (3,3) to (2,3).
The number of houses he passed or arrived during his actions is 1.
Sample Input 2
6 13 4 6 ############# #@@@@@@@@@@@# #@@@@@@@@@@@# #@@@@.@@@@@@# #@@@@@@@@@@@# ############# UURUURLRLUUDDURDURRR
Sample Output 2
3 11 11
Sample Input 3
12 35 7 10 ################################### #.................................# #..........@......................# #......@................@.........# #.............##............@.....# #...##........##....##............# #...##........##....##.......##...# #....##......##......##....##.....# #....##......##......##..##.......# #.....#######.........###.........# #.................................# ################################### LRURRRUUDDULUDUUDLRLRDRRLULRRUDLDRU
Sample Output 3
4 14 1
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
N 棟のビルが等間隔に一列に並んでいます。手前から i 番目のビルの高さは H_i です。
あなたは次の条件をともに満たすようにいくつかのビルを選んで電飾で飾ろうとしています。
- 選んだビルたちは高さが等しい
- 選んだビルたちは等間隔に並んでいる
最大でいくつのビルを選ぶことができますか? なお、ちょうど 1 つのビルを選んだときは条件を満たすとみなします。
制約
- 1 \leq N \leq 3000
- 1 \leq H_i \leq 3000
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N H_1 \ldots H_N
出力
答えを出力せよ。
入力例 1
8 5 7 5 7 7 5 7 7
出力例 1
3
手前から 2,5,8 番目のビルを選ぶと条件を満たします。
入力例 2
10 100 200 300 400 500 600 700 800 900 1000
出力例 2
1
1つのビルを選んだときは条件を満たすとみなします。
入力例 3
32 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5
出力例 3
3
Score : 350 points
Problem Statement
There are N buildings arranged in a line at equal intervals. The height of the i-th building from the front is H_i.
You want to decorate some of these buildings with illuminations so that both of the following conditions are satisfied:
- The chosen buildings all have the same height.
- The chosen buildings are arranged at equal intervals.
What is the maximum number of buildings you can choose? If you choose exactly one building, it is considered to satisfy the conditions.
Constraints
- 1 \leq N \leq 3000
- 1 \leq H_i \leq 3000
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N H_1 \ldots H_N
Output
Print the answer.
Sample Input 1
8 5 7 5 7 7 5 7 7
Sample Output 1
3
Choosing the 2nd, 5th, and 8th buildings from the front satisfies the conditions.
Sample Input 2
10 100 200 300 400 500 600 700 800 900 1000
Sample Output 2
1
Choosing just one building is considered to satisfy the conditions.
Sample Input 3
32 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5
Sample Output 3
3
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
2次元平面上の N 点 (X_1,Y_1),\ldots,(X_N,Y_N) に家が建っています。
最初、点 (S_x,S_y) にサンタクロースがいます。サンタクロースは列 (D_1,C_1),\ldots,(D_M,C_M) に従って以下の行動を行います。
- i=1,2,\ldots,M の順に以下のように移動する。
- 現在サンタクロースがいる点を (x,y) とする。
- D_i が
Uなら、(x,y) から (x,y+C_i) に直線で移動する。 - D_i が
Dなら、(x,y) から (x,y-C_i) に直線で移動する。 - D_i が
Lなら、(x,y) から (x-C_i,y) に直線で移動する。 - D_i が
Rなら、(x,y) から (x+C_i,y) に直線で移動する。
- D_i が
- 現在サンタクロースがいる点を (x,y) とする。
行動を終えたあとにサンタクロースがいる点と、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。
制約
- 1 \leq N \leq 2\times 10^5
- 1 \leq M \leq 2\times 10^5
- -10^9 \leq X_i,Y_i \leq 10^9
- (X_i,Y_i) は相異なる
- -10^9 \leq S_x,S_y \leq 10^9
- (S_x,S_y) に家は建っていない
- D_i は
U,D,L,Rのいずれかである - 1 \leq C_i \leq 10^9
- 与えられる数値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M S_x S_y X_1 Y_1 \vdots X_N Y_N D_1 C_1 \vdots D_M C_M
出力
行動を終えたあとサンタクロースがいる点を (X,Y)、行動により通過または到達した家の数を C とするとき、X,Y,C をこの順に空白区切りで出力せよ。
入力例 1
3 4 3 2 2 2 3 3 2 1 L 2 D 1 R 1 U 2
出力例 1
2 3 2
サンタクロースは以下のように行動します。
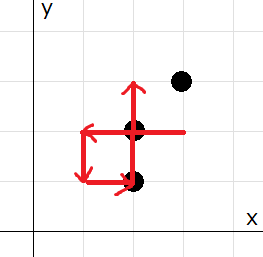
- D_1=
Lなので (3,2) から (3-2,2) に直線で移動する。このとき (2,2) に建っている家を通過する。 - D_2=
Dなので (1,2) から (1,2-1) に直線で移動する。 - D_3=
Rなので (1,1) から (1+1,1) に直線で移動する。このとき (2,1) に建っている家を通過する。 - D_4=
Uなので (2,1) から (2,1+2) に直線で移動する。このとき (2,2) に建っている家を通過するが、この家はすでに通過したことがある家である。
行動により通過または到達した家の数は 2 です。
入力例 2
1 3 0 0 1 1 R 1000000000 R 1000000000 R 1000000000
出力例 2
3000000000 0 0
オーバーフローに注意してください。
Score : 425 points
Problem Statement
There are N houses at points (X_1,Y_1),\ldots,(X_N,Y_N) on a two-dimensional plane.
Initially, Santa Claus is at point (S_x,S_y). He will act according to the sequence (D_1,C_1),\ldots,(D_M,C_M) as follows:
- For i=1,2,\ldots,M in order, he moves as follows:
- Let (x,y) be the point where he currently is.
- If D_i is
U, move in a straight line from (x,y) to (x,y+C_i). - If D_i is
D, move in a straight line from (x,y) to (x,y-C_i). - If D_i is
L, move in a straight line from (x,y) to (x-C_i,y). - If D_i is
R, move in a straight line from (x,y) to (x+C_i,y).
- If D_i is
- Let (x,y) be the point where he currently is.
Find the point where he is after completing all actions, and the number of distinct houses he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.
Constraints
- 1 \leq N \leq 2\times 10^5
- 1 \leq M \leq 2\times 10^5
- -10^9 \leq X_i,Y_i \leq 10^9
- The pairs (X_i,Y_i) are distinct.
- -10^9 \leq S_x,S_y \leq 10^9
- There is no house at (S_x,S_y).
- Each D_i is one of
U,D,L,R. - 1 \leq C_i \leq 10^9
- All input numbers are integers.
Input
The input is given from Standard Input in the following format:
N M S_x S_y X_1 Y_1 \vdots X_N Y_N D_1 C_1 \vdots D_M C_M
Output
Let (X,Y) be the point where he is after completing all actions, and C be the number of distinct houses passed through or arrived at. Print X,Y,C in this order separated by spaces.
Sample Input 1
3 4 3 2 2 2 3 3 2 1 L 2 D 1 R 1 U 2
Sample Output 1
2 3 2
Santa Claus behaves as follows:

- D_1=
L, so he moves from (3,2) to (3-2,2) in a straight line. During this, he passes through the house at (2,2). - D_2=
D, so he moves from (1,2) to (1,2-1) in a straight line. - D_3=
R, so he moves from (1,1) to (1+1,1) in a straight line. During this, he passes through the house at (2,1). - D_4=
U, so he moves from (2,1) to (2,1+2) in a straight line. During this, he passes through the house at (2,2), but it has already been passed.
The number of houses he passed or arrived during his actions is 2.
Sample Input 2
1 3 0 0 1 1 R 1000000000 R 1000000000 R 1000000000
Sample Output 2
3000000000 0 0
Be careful with overflow.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 450 点
問題文
「ユ木」を、以下の手順で生成することができる木と定義します。
- 正整数 x,y を選ぶ
- 頂点を 1 つ用意する
- 別に x 個の頂点を用意し、それぞれを手順 2 で用意した頂点と辺で結ぶ
- 手順 3 で用意した x 個の頂点それぞれに、 y 個の葉をつける
x=4,y=2 のユ木を下図に示します。手順 2,3,4 で用意される頂点をそれぞれ赤、青、緑で示しています。

N 頂点の木 T が与えられます。頂点には 1 から N の番号が付けられており、 i\;(=1,2,\dots,N-1) 番目の辺は頂点 u_i と頂点 v_i を結びます。
T の 0 個以上の頂点とそれに隣接する辺を削除して 1 つのユ木にするとき、削除する頂点数の最小値を求めてください。なお、本問題の制約下で、T をかならずユ木にすることができます。
制約
- 3 \leq N \leq 3 \times 10^5
- 1 \leq u_i < v_i \leq N
- 与えられるグラフは木である
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
出力
答えを出力せよ。
入力例 1
8 1 3 2 3 3 4 4 5 5 6 5 7 4 8
出力例 1
1
頂点 8 を削除することで、与えられた木を x=2,y=2 のユ木にすることができます。
入力例 2
3 1 2 2 3
出力例 2
0
与えられた木はすでに x=1,y=1 のユ木です。
入力例 3
10 1 3 1 2 5 7 6 10 2 8 1 6 8 9 2 7 1 4
出力例 3
3
Score : 450 points
Problem Statement
A "Snowflake Tree" is defined as a tree that can be generated by the following procedure:
- Choose positive integers x,y.
- Prepare one vertex.
- Prepare x more vertices, and connect each of them to the vertex prepared in step 2.
- For each of the x vertices prepared in step 3, attach y leaves to it.
The figure below shows a Snowflake Tree with x=4,y=2. The vertices prepared in steps 2, 3, 4 are shown in red, blue, and green, respectively.

You are given a tree T with N vertices. The vertices are numbered 1 to N, and the i-th edge (i=1,2,\dots,N-1) connects vertices u_i and v_i.
Consider deleting zero or more vertices of T and the edges adjacent to them so that the remaining graph becomes a single Snowflake Tree. Find the minimum number of vertices that must be deleted. Under the constraints of this problem, it is always possible to transform T into a Snowflake Tree.
Constraints
- 3 \leq N \leq 3 \times 10^5
- 1 \leq u_i < v_i \leq N
- The given graph is a tree.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
Output
Print the answer.
Sample Input 1
8 1 3 2 3 3 4 4 5 5 6 5 7 4 8
Sample Output 1
1
By deleting vertex 8, the given tree can be transformed into a Snowflake Tree with x=2,y=2.
Sample Input 2
3 1 2 2 3
Sample Output 2
0
The given tree is already a Snowflake Tree with x=1,y=1.
Sample Input 3
10 1 3 1 2 5 7 6 10 2 8 1 6 8 9 2 7 1 4
Sample Output 3
3
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
1 から N の番号がついた N 棟のビルが数直線上に建っています。
ビル i は座標 X_i にあり、高さは H_i です。ビルの高さ方向以外の大きさは無視できるものとします。
座標 x の高さ h の地点 P からビル i が見えるとは、ビル i 上のある点 Q であって、線分 PQ が他のビルと共有点を持たないものが存在することと定めます。
座標 0 から全てのビルを見ることができない高さの最大値を求めてください。ただし、高さは非負の値を取るとし、高さ 0 で全てのビルを見ることができる場合はかわりに -1 と答えてください。
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq X_1 < \dots < X_N \leq 10^9
- 1 \leq H_i \leq 10^9
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N X_1 H_1 \vdots X_N H_N
出力
座標 0、高さ 0 の地点から全てのビルを見ることができる場合は -1 と出力せよ。
そうでないとき、座標 0 から全てのビルを見ることができない高さの最大値を出力せよ。真の解との絶対誤差または相対誤差が 10^{-9} 以下のとき正解と判定される。
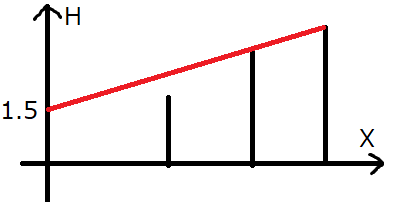
入力例 1
3 3 2 5 4 7 5
出力例 1
1.500000000000000000
座標 0 高さ 1.5 の位置ではビル 3 を見ることができません。高さが 1.5 より僅かでも高ければビル 3 を含む全てのビルを見ることができるため、答えは 1.5 です。
入力例 2
2 1 1 2 100
出力例 2
-1
-1.000 などの出力では不正解となることに注意してください。
入力例 3
3 1 1 2 2 3 3
出力例 3
0.000000000000000000
入力例 4
4 10 10 17 5 20 100 27 270
出力例 4
17.142857142857142350
Score : 525 points
Problem Statement
There are N buildings numbered 1 to N on a number line.
Building i is at coordinate X_i and has height H_i. The size in directions other than height is negligible.
From a point P with coordinate x and height h, building i is considered visible if there exists a point Q on building i such that the line segment PQ does not intersect with any other building.
Find the maximum height at coordinate 0 from which it is not possible to see all buildings. Height must be non-negative; if it is possible to see all buildings at height 0 at coordinate 0, report -1 instead.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq X_1 < \dots < X_N \leq 10^9
- 1 \leq H_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X_1 H_1 \vdots X_N H_N
Output
If it is possible to see all buildings from coordinate 0 and height 0, print -1. Otherwise, print the maximum height at coordinate 0 from which it is not possible to see all buildings. Answers with an absolute or relative error of at most 10^{-9} from the true answer will be considered correct.
Sample Input 1
3 3 2 5 4 7 5
Sample Output 1
1.500000000000000000
From coordinate 0 and height 1.5, building 3 cannot be seen. If the height is even slightly greater than 1.5, all buildings including building 3 can be seen. Thus, the answer is 1.5.

Sample Input 2
2 1 1 2 100
Sample Output 2
-1
Note that -1.000 or similar outputs would be considered incorrect.
Sample Input 3
3 1 1 2 2 3 3
Sample Output 3
0.000000000000000000
Sample Input 4
4 10 10 17 5 20 100 27 270
Sample Output 4
17.142857142857142350
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
(1,2,\dots,N) の並び替え P=(P_1,P_2,\dots,P_N) に対し、整数 L(P),R(P) を以下のように定めます。
- N 個のビルが左右一列に並んでおり、左から i 番目のビルの高さは P_i であるとする。このビルの列を左側から見たときに見えるビルの数を L(P)、右側から見たときに見えるビルの数を R(P) とする。
より形式的には、L(P) はすべての j<i に対して P_j < P_i を満たす i の個数であり、 R(P) はすべての j > i に対して P_i > P_j を満たす i の個数である。
整数 N,K が与えられます。(1,2,\dots,N) の並び替え P であって、L(P)-R(P)=K となるようなものの個数を 998244353 で割ったあまりを求めてください。
制約
- 1 \leq N \leq 2 \times 10^5
- |K| \leq N-1
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N K
出力
答えを出力せよ。
入力例 1
3 -1
出力例 1
1
- P=(1,2,3): L(P)-R(P)=3-1=2 です。
- P=(1,3,2): L(P)-R(P)=2-2=0 です。
- P=(2,1,3): L(P)-R(P)=2-1=1 です。
- P=(2,3,1): L(P)-R(P)=2-2=0 です。
- P=(3,1,2): L(P)-R(P)=1-2=-1 です。
- P=(3,2,1): L(P)-R(P)=1-3=-2 です。
よって、L(P)-R(P)=-1 となる P の個数は 1 です。
入力例 2
1 0
出力例 2
1
入力例 3
2024 385
出力例 3
576300012
998244353 で割ったあまりを出力してください。
Score : 600 points
Problem Statement
For a permutation P=(P_1,P_2,\dots,P_N) of (1,2,\dots,N), define integers L(P) and R(P) as follows:
- Consider N buildings arranged in a row from left to right, with the height of the i-th building from the left being P_i. Then L(P) is the number of buildings visible when viewed from the left, and R(P) is the number of buildings visible when viewed from the right.
More formally, L(P) is the count of indices i such that P_j < P_i for all j < i, and R(P) is the count of indices i such that P_i > P_j for all j > i.
You are given integers N and K. Find, modulo 998244353, the count of all permutations P of (1,2,\dots,N) such that L(P)-R(P)=K.
Constraints
- 1 \leq N \leq 2 \times 10^5
- |K| \leq N-1
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N K
Output
Print the answer.
Sample Input 1
3 -1
Sample Output 1
1
- P=(1,2,3): L(P)-R(P)=3-1=2.
- P=(1,3,2): L(P)-R(P)=2-2=0.
- P=(2,1,3): L(P)-R(P)=2-1=1.
- P=(2,3,1): L(P)-R(P)=2-2=0.
- P=(3,1,2): L(P)-R(P)=1-2=-1.
- P=(3,2,1): L(P)-R(P)=1-3=-2.
Therefore, the number of permutations P with L(P)-R(P)=-1 is 1.
Sample Input 2
1 0
Sample Output 2
1
Sample Input 3
2024 385
Sample Output 3
576300012
Print the count modulo 998244353.