実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 個の箱が横一列に並んでおり、そのうちのいくつかの箱にはクッキーが入っています。
各箱の状態は長さ N の文字列 S によって表されます。
具体的には、左から i\ (1\leq i\leq N) 番目の箱は、S の i 文字目が @ のときクッキーが 1 枚入っており、. のとき空き箱です。
高橋君は今からの D 日間、一日一回ずつ、これらの箱のいずれかに入ったクッキーを 1 枚選んで食べます。
N 個の箱のうち、D 日間が経過した後に空き箱であるものはいくつあるか求めてください。 (この値は高橋君が各日でどのクッキーを選ぶかによらないことが証明できます。)
なお、S には @ が D 個以上含まれることが保証されます。
制約
- 1\leq D \leq N \leq 100
- N,D は整数
- S は
@と.からなる長さ N の文字列 - S には
@が D 個以上含まれる
入力
入力は以下の形式で標準入力から与えられる。
N D S
出力
N 個の箱のうち、D 日間が経過した後に空き箱であるものの個数を出力せよ。
入力例 1
5 2 .@@.@
出力例 1
4
例えば、高橋君は以下のように行動する可能性があります。
- 1 日目:左から 2,3,5 番目の箱にクッキーが入っている。左から 2 番目の箱に入っているクッキーを選んで食べる。
- 2 日目:左から 3,5 番目の箱にクッキーが入っている。左から 5 番目の箱に入っているクッキーを選んで食べる。
- 2 日間が経過した後、左から 3 番目の箱にのみクッキーが入っている。よって、5 個の箱のうち 4 箱が空き箱である。
高橋君が各日で選ぶクッキーはこの例とは異なる可能性もありますが、いずれにせよ 2 日間が経過した後には 4 箱が空き箱です。 よって答えは 4 です。
入力例 2
3 3 @@@
出力例 2
3
入力例 3
10 4 @@@.@@.@@.
出力例 3
7
Score: 100 points
Problem Statement
There are N boxes arranged in a row, and some of these boxes contain cookies.
The state of these boxes is represented by a string S of length N.
Specifically, the i-th box (1\leq i \leq N) from the left contains one cookie if the i-th character of S is @, and is empty if it is ..
Over the next D days, Takahashi will choose and eat one cookie per day from among the cookies in these boxes.
Determine how many of the N boxes will be empty after D days have passed. (It can be proved that this value does not depend on which cookies Takahashi chooses each day.)
It is guaranteed that S contains at least D occurrences of @.
Constraints
- 1 \leq D \leq N \leq 100
- N and D are integers.
- S is a string of length N consisting of
@and.. - S contains at least D occurrences of
@.
Input
The input is given from Standard Input in the following format:
N D S
Output
Print the number of boxes that will be empty after D days have passed among the N boxes.
Sample Input 1
5 2 .@@.@
Sample Output 1
4
For example, Takahashi might act as follows:
- Day 1: There are cookies in the 2nd, 3rd, and 5th boxes from the left. He chooses the cookie in the 2nd box to eat.
- Day 2: There are cookies in the 3rd and 5th boxes. He chooses the cookie in the 5th box to eat.
- After two days have passed, only the 3rd box from the left contains a cookie. Therefore, four out of the five boxes are empty.
Even though Takahashi might choose differently on each day than in this example, there will still be four empty boxes after two days. Therefore, the answer is 4.
Sample Input 2
3 3 @@@
Sample Output 2
3
Sample Input 3
10 4 @@@.@@.@@.
Sample Output 3
7
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
A 問題と似た設定の問題です。A 問題とは、高橋君が食べるクッキーの選び方および求めるものが異なります。
N 個の箱が横一列に並んでおり、そのうちのいくつかの箱にはクッキーが入っています。
各箱の状態は長さ N の文字列 S によって表されます。
具体的には、左から i\ (1\leq i\leq N) 番目の箱は、S の i 文字目が @ のときクッキーが 1 枚入っており、. のとき空き箱です。
高橋君は今からの D 日間、一日一回ずつ、その時点でクッキーが入っている箱のうち最も右にある箱のクッキーを選んで食べます。
N 個の箱それぞれについて、D 日間が経過した後にその箱にクッキーが入っているかを求めてください。
なお、S には @ が D 個以上含まれることが保証されます。
制約
- 1\leq D \leq N \leq 100
- N,D は整数
- S は
@と.からなる長さ N の文字列 - S には
@が D 個以上含まれる
入力
入力は以下の形式で標準入力から与えられる。
N D S
出力
長さ N の文字列を出力せよ。
出力する文字列の i\ (1\leq i\leq N) 文字目は、D 日間が経過した後に左から i 番目の箱にクッキーが入っているならば @、入っていないならば . とせよ。
入力例 1
5 2 .@@.@
出力例 1
.@...
高橋君は以下のように行動します。
- 1 日目:左から 2,3,5 番目の箱にクッキーが入っている。このうちで最も右にある、左から 5 番目の箱に入っているクッキーを選んで食べる。
- 2 日目:左から 2,3 番目の箱にクッキーが入っている。このうちで最も右にある、左から 3 番目の箱に入っているクッキーを選んで食べる。
- 2 日間が経過した後、左から 2 番目の箱にのみクッキーが入っている。
よって、正しい出力は .@... です。
入力例 2
3 3 @@@
出力例 2
...
入力例 3
10 4 @@@.@@.@@.
出力例 3
@@@.......
Score: 200 points
Problem Statement
This problem shares a similar setting with Problem A. The way Takahashi chooses cookies and what you are required to find are different from Problem A.
There are N boxes arranged in a row, and some of these boxes contain cookies.
The state of these boxes is represented by a string S of length N.
Specifically, the i-th box (1\leq i \leq N) from the left contains one cookie if the i-th character of S is @, and is empty if it is ..
Over the next D days, Takahashi will choose and eat one cookie per day from among the cookies in these boxes. On each day, he chooses the cookie in the rightmost box that contains a cookie at that point.
Determine, for each of the N boxes, whether it will contain a cookie after D days have passed.
It is guaranteed that S contains at least D occurrences of @.
Constraints
- 1 \leq D \leq N \leq 100
- N and D are integers.
- S is a string of length N consisting of
@and.. - S contains at least D occurrences of
@.
Input
The input is given from Standard Input in the following format:
N D S
Output
Print a string of length N.
The i-th character (1 \leq i \leq N) of the string should be @ if the i-th box from the left contains a cookie after D days have passed, and . otherwise.
Sample Input 1
5 2 .@@.@
Sample Output 1
.@...
Takahashi acts as follows:
- Day 1: There are cookies in the 2nd, 3rd, and 5th boxes from the left. Among these, the rightmost is the 5th box. He eats the cookie in this box.
- Day 2: There are cookies in the 2nd and 3rd boxes. Among these, the rightmost is the 3rd box. He eats the cookie in this box.
- After two days have passed, only the 2nd box from the left contains a cookie.
Therefore, the correct output is .@....
Sample Input 2
3 3 @@@
Sample Output 2
...
Sample Input 3
10 4 @@@.@@.@@.
Sample Output 3
@@@.......
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 350 点
問題文
とある回転寿司に、1 から N までの番号が付けられた N 人の人が訪れています。 人 i の 美食度 は A_i です。
今からベルトコンベア上を M 個の寿司が流れます。 j 番目に流れる寿司の 美味しさ は B_j です。 それぞれの寿司は、人 1,2,\dots,N の前をこの順に流れていきます。 それぞれの人は、美味しさが自分の美食度以上である寿司が自分の前に流れてきたときはその寿司を取って食べ、それ以外のときは何もしません。 人 i が取って食べた寿司は、人 j\ (j > i) の前にはもう流れてきません。
M 個の寿司それぞれについて、その寿司を誰が食べるか、あるいは誰も食べないかどうかを求めてください。
制約
- 1\leq N,M \leq 2\times 10^5
- 1\leq A_i,B_i \leq 2\times 10^5
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 \dots A_N B_1 B_2 \dots B_M
出力
M 行出力せよ。
j\ (1\leq j \leq M) 行目には、j 番目に流れる寿司を食べる人がいるならばその人の番号を、そうでないならば -1 を出力せよ。
入力例 1
3 3 3 8 2 5 2 1
出力例 1
1 3 -1
- 1 番目の寿司について、
- まず人 1 の前を流れます。B_1 \geq A_1 なので、人 1 はこれを取って食べます。
- 人 2,3 の前にはこの寿司は流れてきません。
- 2 番目の寿司について、
- まず人 1 の前を流れます。B_2 < A_1 なので、人 1 は何もしません。
- 次に人 2 の前を流れます。B_2 < A_2 なので、人 2 は何もしません。
- 最後に人 3 の前を流れます。B_2 \geq A_3 なので、人 3 はこれを取って食べます。
- 3 番目の寿司について、
- まず人 1 の前を流れます。B_3 < A_1 なので、人 1 は何もしません。
- 次に人 2 の前を流れます。B_3 < A_2 なので、人 2 は何もしません。
- 最後に人 3 の前を流れます。B_3 < A_3 なので、人 3 は何もしません。
- よって、誰もこの寿司を食べません。
入力例 2
3 3 1 1 1 1 1 1
出力例 2
1 1 1
入力例 3
10 5 60 83 76 45 70 91 37 58 94 22 70 39 52 33 18
出力例 3
1 7 4 10 -1
Score: 350 points
Problem Statement
There are N people numbered from 1 to N visiting a conveyor belt sushi restaurant. The gourmet level of person i is A_i.
Now, M pieces of sushi will be placed on the conveyor belt. The deliciousness of the j-th sushi is B_j. Each piece of sushi passes in front of people 1, 2, \dots, N in this order. Each person, when a sushi whose deliciousness is not less than their gourmet level passes in front of them, will take and eat that sushi; otherwise, they do nothing. A sushi that person i takes and eats will no longer pass in front of person j\ (j > i).
For each of the M pieces of sushi, determine who eats that sushi, or if nobody eats it.
Constraints
- 1 \leq N, M \leq 2 \times 10^5
- 1 \leq A_i, B_i \leq 2 \times 10^5
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 A_2 \dots A_N B_1 B_2 \dots B_M
Output
Print M lines.
The j-th line (1 \leq j \leq M) should contain the number representing the person who eats the j-th sushi, or -1 if nobody eats it.
Sample Input 1
3 3 3 8 2 5 2 1
Sample Output 1
1 3 -1
- For the 1st sushi:
- It first passes in front of person 1. Since B_1 \geq A_1, person 1 takes and eats it.
- It will not pass in front of person 2 and 3.
- For the 2nd sushi:
- It first passes in front of person 1. Since B_2 < A_1, person 1 does nothing.
- Next, it passes in front of person 2. Since B_2 < A_2, person 2 does nothing.
- Finally, it passes in front of person 3. Since B_2 \geq A_3, person 3 takes and eats it.
- For the 3rd sushi:
- It first passes in front of person 1. Since B_3 < A_1, person 1 does nothing.
- Next, it passes in front of person 2. Since B_3 < A_2, person 2 does nothing.
- Finally, it passes in front of person 3. Since B_3 < A_3, person 3 does nothing.
- Therefore, nobody eats this sushi.
Sample Input 2
3 3 1 1 1 1 1 1
Sample Output 2
1 1 1
Sample Input 3
10 5 60 83 76 45 70 91 37 58 94 22 70 39 52 33 18
Sample Output 3
1 7 4 10 -1
実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
整数 N と M が与えられます。
以下の条件をすべて満たす長さ N の整数列 (A_1, A_2, \ldots, A_N) を辞書順にすべて出力してください。
- 1 \leq A_i
- 2 以上 N 以下の各整数 i に対して A_{i - 1} + 10 \leq A_i
- A_N \leq M
数列の辞書順とは
長さ N の数列 S = (S_1, S_2, \ldots, S_N) が長さ N の数列 T = (T_1, T_2, \ldots, T_N) より辞書順で小さいとは、ある整数 1 \leq i \leq N が存在して下記の 2 つがともに成り立つことをいいます。
- (S_1, S_2, \ldots, S_{i-1}) = (T_1, T_2, \ldots, T_{i-1})
- S_i が T_i より(数として)小さい。
制約
- 2 \leq N \leq 12
- 10N - 9 \leq M \leq 10N
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M
出力
条件を満たす長さ N の整数列の個数を X として X + 1 行出力せよ。
1 行目には X の値を出力せよ。
i + 1 (1 \leq i \leq X) 行目には条件を満たす整数列のうち辞書順で i 番目に小さいものを空白区切りで出力せよ。
入力例 1
3 23
出力例 1
10 1 11 21 1 11 22 1 11 23 1 12 22 1 12 23 1 13 23 2 12 22 2 12 23 2 13 23 3 13 23
(1, 11, 21), (1, 11, 22), (1, 11, 23), (1, 12, 22), (1, 12, 23), (1, 13, 23), (2, 12, 22), (2, 12, 23), (2, 13, 23), (3, 13, 23) の 10 個の数列が条件を満たします。
Score: 425 points
Problem Statement
You are given integers N and M.
Print all integer sequences (A_1, A_2, \ldots, A_N) of length N that satisfy all of the following conditions, in lexicographical order.
- 1 \leq A_i
- A_{i - 1} + 10 \leq A_i for each integer i from 2 through N
- A_N \leq M
What is lexicographical order?
A sequence S = (S_1, S_2, \ldots, S_N) of length N is smaller in lexicographical order than a sequence T = (T_1, T_2, \ldots, T_N) of length N if and only if there exists an integer 1 \leq i \leq N such that both of the following hold:
- (S_1, S_2, \ldots, S_{i-1}) = (T_1, T_2, \ldots, T_{i-1})
- S_i is less than T_i (as a number).
Constraints
- 2 \leq N \leq 12
- 10N - 9 \leq M \leq 10N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M
Output
Let X be the number of integer sequences that satisfy the conditions, and print X + 1 lines.
The first line should contain the value of X.
The (i + 1)-th line (1 \leq i \leq X) should contain the i-th smallest integer sequence in lexicographical order, with elements separated by spaces.
Sample Input 1
3 23
Sample Output 1
10 1 11 21 1 11 22 1 11 23 1 12 22 1 12 23 1 13 23 2 12 22 2 12 23 2 13 23 3 13 23
(1, 11, 21), (1, 11, 22), (1, 11, 23), (1, 12, 22), (1, 12, 23), (1, 13, 23), (2, 12, 22), (2, 12, 23), (2, 13, 23), (3, 13, 23) are the 10 sequences that satisfy the conditions.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 475 点
問題文
N 枚のカードが入ったパックが無限にあります。各パックについて、i 枚目に入っているカードは P_i\% の確率でレアです。また、各カードがレアであることは他のカードがレアであることと独立です。
これからパックを一つずつ開封していき、開封したパックに入っているすべてのカードを手に入れます。レアカードを合計 X 枚以上手に入れるまでパックを開封するとき、開封するパックの個数の期待値を求めてください。
制約
- 1 \leq N \leq 5000
- 1 \leq X \leq 5000
- 1 \leq P_i \leq 100
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N X P_1 P_2 \ldots P_N
出力
答えを出力せよ。
真の答えとの絶対誤差または相対誤差が 10^{-6} 以下ならば正解と判定される。
入力例 1
2 2 50 100
出力例 1
1.5000000000000000
開封するパックの個数は \frac{1}{2} の確率で 1 個、\frac{1}{2} の確率で 2 個となります。
入力例 2
2 3 40 60
出力例 2
3.2475579530543811
入力例 3
6 3 10 33 33 10 100 10
出力例 3
1.8657859189536100
Score: 475 points
Problem Statement
There are infinitely many packs, each containing N cards. In each pack, the i-th card is rare with probability P_i percent. Whether each card is rare is independent of other cards being rare.
You will now open the packs one by one, and obtain all the cards in each opened pack. When you keep opening packs until you have obtained a total of at least X rare cards, find the expected number of packs you will open.
Constraints
- 1 \leq N \leq 5000
- 1 \leq X \leq 5000
- 1 \leq P_i \leq 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X P_1 P_2 \ldots P_N
Output
Print the answer.
Your answer will be considered correct if the absolute or relative error from the true answer is at most 10^{-6}.
Sample Input 1
2 2 50 100
Sample Output 1
1.5000000000000000
The number of packs opened will be 1 with probability \frac{1}{2}, and 2 with probability \frac{1}{2}.
Sample Input 2
2 3 40 60
Sample Output 2
3.2475579530543811
Sample Input 3
6 3 10 33 33 10 100 10
Sample Output 3
1.8657859189536100
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 525 点
問題文
H 行 W 列のグリッドがあります。 このグリッドの上から i\ (1\leq i\leq H) 行目、左から j\ (1\leq j\leq W) 列目のマスを (i,j) と表記します。
1 から N までの番号が付けられた N 個の横長のバーがグリッド上に置かれています。 バー i は 1\times 1 のブロックが横に L_i 個繋がった形をしており、その左端のブロックは最初マス (R_i,C_i) 上にあります。 すなわち、バー i は最初マス (R_i,C_i), (R_i,C_i+1), \dots, (R_i,C_i+L_i-1) を占めています。 ここで、相異なる 2 つのバーに占められているマスは存在しないことが保証されます。
現在の時刻は t=0 です。 非負整数 n を用いて t=0.5+n と表されるようなすべての時刻において、i=1,2,\dots,N の順に以下のことが起こります。
- バー i が一番下の行(H 行目)になく、かつバー i が占める各マスの 1 つ下のマスをどのバーも占めていない場合、バー i 全体が 1 マス分下に移動する。 すなわち、その時点でバー i が占めているマスが (r,C_i),(r,C_i+1),\dots,(r,C_i+L_i-1)\ (r < H) であり、どの j\ (0\leq j\leq L_i-1) についてもマス (r+1,C_i+j) を占めているバーが存在しないならば、 バー i の占めるマスが (r+1,C_i),(r+1,C_i+1),\dots,(r+1,C_i+L_i-1) に変化する。
- そうでないならば、何も起こらない。
t=10^{100} においてバー i が占めているマスを (R'_i,C_i), (R'_i,C_i+1), \dots, (R'_i,C_i+L_i-1) とします。 R'_1,R'_2,\dots,R'_N を求めてください。
制約
- 1\leq H,W \leq 2\times 10^5
- 1\leq N \leq 2\times 10^5
- 1\leq R_i\leq H
- 1\leq C_i\leq W
- 1\leq L_i\leq W-C_i+1
- 与えられる初期状態において、相異なる 2 つのバーに占められているマスは存在しない
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
H W N R_1 C_1 L_1 R_2 C_2 L_2 \vdots R_N C_N L_N
出力
N 行出力せよ。 i\ (1\leq i \leq N) 行目には、R'_i を出力せよ。
入力例 1
4 4 4 1 2 3 3 2 2 2 1 2 2 4 1
出力例 1
2 4 3 4
以下の 3 つの図は左から順に t=0,1,2 でのグリッドの様子を表しています。 色の塗られた長方形は各バーを表し、長方形の中に書かれた数字はそのバーの番号です。
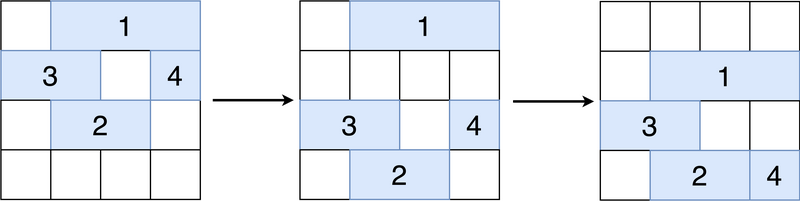
グリッドの状態の変化は以下の通り説明されます。
- t=0.5:
- i=1: バー 1 が占める各マスの 1 つ下のマスである (2,2),(2,3),(2,4) のうち、(2,2) がバー 3 に、(2,4) がバー 4 にそれぞれ占められているため、何も起こらない。
- i=2: バー 2 が占める各マスの 1 つ下のマスである (4,2),(4,3) がいずれも他のバーに占められていないため、バー 2 全体が 1 マス分下に移動する。
- i=3: バー 3 が占める各マスの 1 つ下のマスである (3,1),(3,2) がいずれも他のバーに占められていないため、バー 3 全体が 1 マス分下に移動する。
- i=4: バー 4 が占めるマスの 1 つ下のマスである (3,4) が他のバーに占められていないため、バー 4 全体が 1 マス分下に移動する。
- t=1.5:
- i=1: バー 1 が占める各マスの 1 つ下のマスである (2,2),(2,3),(2,4) がいずれも他のバーに占められていないため、バー 1 全体が 1 マス分下に移動する。
- i=2: バー 2 は一番下の行にあるため、何も起こらない。
- i=3: バー 3 が占める各マスの 1 つ下のマスである (4,1),(4,2) のうち、(4,2) がバー 2 に占められているため、何も起こらない。
- i=4: バー 4 が占めるマスの 1 つ下のマスである (4,4) が他のバーに占められていないため、バー 4 全体が 1 マス分下に移動する。
t=2.5,3.5,\dots においては 1 つ下のマスがすべて空いているようなバーが存在せず、何も起こらないため、t=10^{100} でのグリッドの状態は t=2 でのグリッドの状態(上図における一番右の状態)と同じです。
よって、R'_1=2,R'_2=4,R'_3=3,R'_4=4 です。
入力例 2
382 382 3 3 3 3 8 8 8 2 2 2
出力例 2
382 382 381
入力例 3
5 10 8 2 2 1 4 3 1 4 8 2 1 2 2 2 5 3 5 4 3 4 5 2 1 5 2
出力例 3
5 5 5 4 3 5 4 2
Score: 525 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
There are N horizontal bars numbered from 1 to N placed on the grid. Bar i consists of L_i blocks of size 1 \times 1 connected horizontally, and its leftmost block is initially at cell (R_i, C_i). That is, initially, bar i occupies the cells (R_i, C_i), (R_i, C_i + 1), \dots, (R_i, C_i + L_i - 1). It is guaranteed that there is no cell occupied by two different bars.
The current time is t = 0. At every time t = 0.5 + n for some non-negative integer n, the following occurs in order of i = 1, 2, \dots, N:
- If bar i is not on the bottom row (the H-th row), and none of the cells directly below the cells occupied by bar i is occupied by any bar, then bar i moves down by one cell. That is, if at that time bar i occupies the cells (r,C_i),(r,C_i+1),\dots,(r,C_i+L_i-1)\ (r < H), and the cell (r + 1, C_i + j) is not occupied by any bar for all j (0 \leq j \leq L_i - 1), then bar i now occupies (r + 1, C_i), (r + 1, C_i + 1), \dots, (r + 1, C_i + L_i - 1).
- Otherwise, nothing happens.
Let (R'_i, C_i), (R'_i, C_i + 1), \dots, (R'_i, C_i + L_i - 1) be the cells occupied by bar i at time t = 10^{100}. Find R'_1, R'_2, \dots, R'_N.
Constraints
- 1 \leq H, W \leq 2 \times 10^5
- 1 \leq N \leq 2 \times 10^5
- 1 \leq R_i \leq H
- 1 \leq C_i \leq W
- 1 \leq L_i \leq W - C_i + 1
- In the initial state, there is no cell occupied by two different bars.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H W N R_1 C_1 L_1 R_2 C_2 L_2 \vdots R_N C_N L_N
Output
Print N lines. The i-th line (1 \leq i \leq N) should contain R'_i.
Sample Input 1
4 4 4 1 2 3 3 2 2 2 1 2 2 4 1
Sample Output 1
2 4 3 4
The following three diagrams represent the grid at times t = 0, 1, and 2 from left to right. Colored rectangles represent the bars, and the number inside each rectangle indicates its bar number.

The changes in the grid state are explained as follows:
- At t = 0.5:
- i = 1: The cells directly below bar 1 are (2,2),(2,3),(2,4). Among these, (2,2) is occupied by bar 3 and (2,4) is occupied by bar 4, so nothing happens.
- i = 2: The cells directly below bar 2 are (4,2),(4,3), which are not occupied by any other bar, so bar 2 moves down by one cell.
- i = 3: The cells directly below bar 3 are (3,1),(3,2), which are not occupied by any other bar, so bar 3 moves down by one cell.
- i = 4: The cell directly below bar 4 is (3,4), which is not occupied by any other bar, so bar 4 moves down by one cell.
- At t = 1.5:
- i = 1: The cells directly below bar 1 are (2,2),(2,3),(2,4), which are not occupied by any other bar, so bar 1 moves down by one cell.
- i = 2: Bar 2 is on the bottom row, so nothing happens.
- i = 3: The cells directly below bar 3 are (4,1),(4,2). Among these, (4,2) is occupied by bar 2, so nothing happens.
- i = 4: The cell directly below bar 4 is (4,4), which is not occupied by any other bar, so bar 4 moves down by one cell.
At times t = 2.5, 3.5, \dots, there is no bar such that the cells directly below it are all unoccupied, so nothing happens. Thus, the grid at time t = 10^{100} is the same as at t = 2 (the rightmost diagram above).
Therefore, R'_1 = 2, R'_2 = 4, R'_3 = 3, R'_4 = 4.
Sample Input 2
382 382 3 3 3 3 8 8 8 2 2 2
Sample Output 2
382 382 381
Sample Input 3
5 10 8 2 2 1 4 3 1 4 8 2 1 2 2 2 5 3 5 4 3 4 5 2 1 5 2
Sample Output 3
5 5 5 4 3 5 4 2
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 575 点
問題文
二次元座標平面上にタイルが敷き詰められています。
各タイルの形は長方形であり、0 \leq k < K を満たす各整数組 (i, j, k) に対して以下のような規則で対応するタイルが配置されています。
-
i と j の偶奇が一致しているとき、(i, j, k) に対応するタイルは iK \leq x \leq (i + 1)K かつ jK + k \leq y \leq jK + k + 1 なる範囲の (x, y) を覆う。
-
i と j の偶奇が一致していないとき、(i, j, k) に対応するタイルは iK + k \leq x \leq iK + k + 1 かつ jK \leq y \leq (j + 1)K なる範囲の (x, y) を覆う。
2 つのタイルが隣接していることを 2 つのタイルの辺が正の長さの共通部分を持つことにより定義します。
(S_x + 0.5, S_y + 0.5) を含むタイルから隣接しているタイルに移動することを繰り返して (T_x + 0.5, T_y + 0.5) を含むタイルに移動するとき、隣接するタイルに移動する回数の最小値を求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1 \leq T \leq 10^4
- 2 \leq K \leq 10^{16}
- -10^{16} \leq S_x, S_y, T_x, T_y \leq 10^{16}
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられる。
K S_x S_y T_x T_y
出力
T 行出力せよ。i 行目には i 番目のテストケースに対する答えを出力せよ。
入力例 1
3 3 -2 1 4 -1 4 8 8 0 2 5 -1000000000000 -1000000000000 1000000000000 1000000000000
出力例 1
4 4 800000000000
1 番目のテストケースについて説明します。
整数組 (i, j, k) に対応するタイルを単にタイル (i, j, k) と表記します。
(-1.5, 1.5) はタイル (-1, 0, 1) に含まれ、(4.5, -0.5) はタイル (1, -1, 2) に含まれます。
例えば、タイル (-1, 0, 1) \to (-1, 0, 2) \to (0, 0, 2) \to (1, 0, 0) \to (1, -1, 2) という移動をすることによって、4 回の隣接するタイルへの移動でタイル (1, -1, 2) に辿り着くことができます。
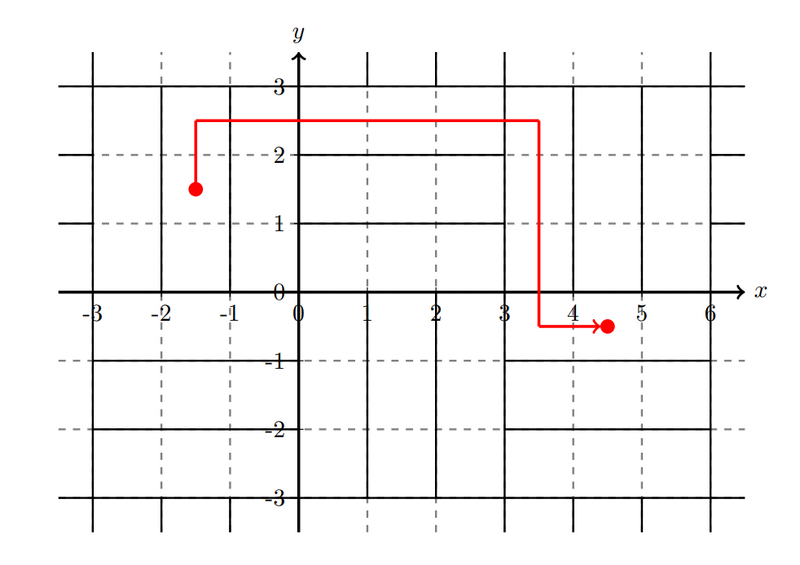
Score: 575 points
Problem Statement
Tiles are laid out covering the two-dimensional coordinate plane.
Each tile is a rectangle, and for each integer triple (i, j, k) satisfying 0 \leq k < K, a corresponding tile is placed according to the following rules:
- When i and j have the same parity (both even or both odd), the tile corresponding to (i, j, k) covers the area where iK \leq x \leq (i + 1)K and jK + k \leq y \leq jK + k + 1.
- When i and j have different parity, the tile corresponding to (i, j, k) covers the area where iK + k \leq x \leq iK + k + 1 and jK \leq y \leq (j + 1)K.
Two tiles are adjacent when their edges have a common segment of positive length.
Starting from the tile containing the point (S_x + 0.5, S_y + 0.5), find the minimum number of times you need to move to an adjacent tile to reach the tile containing the point (T_x + 0.5, T_y + 0.5).
There are T test cases; solve each of them.
Constraints
- 1 \leq T \leq 10^4
- 2 \leq K \leq 10^{16}
- -10^{16} \leq S_x, S_y, T_x, T_y \leq 10^{16}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
K S_x S_y T_x T_y
Output
Print T lines. The i-th line should contain the answer for the i-th test case.
Sample Input 1
3 3 -2 1 4 -1 4 8 8 0 2 5 -1000000000000 -1000000000000 1000000000000 1000000000000
Sample Output 1
4 4 800000000000
Let us explain the first test case.
Let (i, j, k) denote the tile corresponding to integer triple (i, j, k).
(-1.5, 1.5) is contained in tile (-1, 0, 1), and (4.5, -0.5) is contained in tile (1, -1, 2).
For example, by moving from tile (-1, 0, 1) to (-1, 0, 2) to (0, 0, 2) to (1, 0, 0) to (1, -1, 2), you can reach tile (1, -1, 2) in four moves to an adjacent tile.
